2023-2024学年鲁教版(五四制)七年级数学上册 第1—3章 阶段性综合练习题(含解析)
文档属性
| 名称 | 2023-2024学年鲁教版(五四制)七年级数学上册 第1—3章 阶段性综合练习题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 202.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 20:02:32 | ||
图片预览

文档简介
2023-2024学年鲁教版七年级数学上册《第1—3章》阶段性综合练习题(附答案)
一、选择题(共36分)
1.如果一个三角形是轴对称图形,那么这个三角形一定是( )
A.直角三角形 B.等腰直角三角形
C.等边三角形 D.等腰三角形
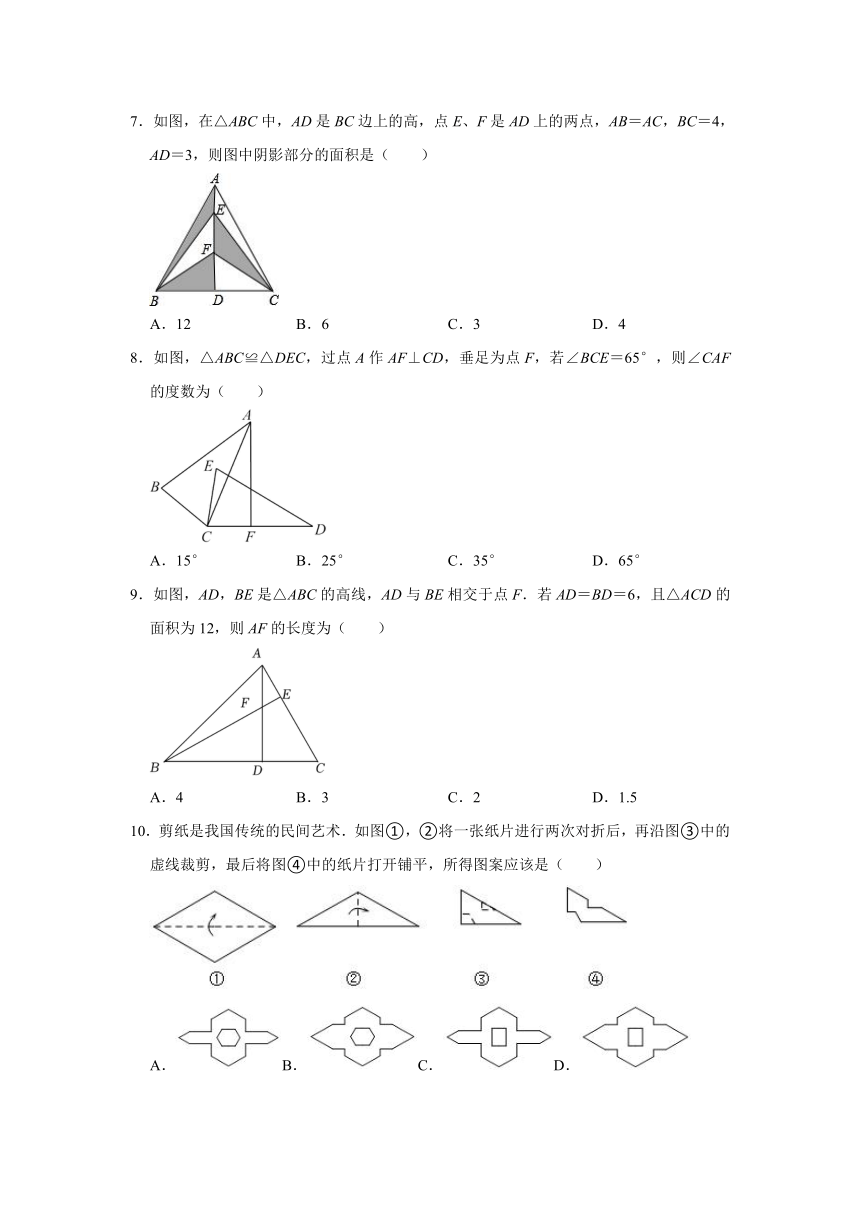
2.如图所示在△ABC中,AB边上的高线画法正确的是( )
A. B.
C. D.
3.下列长度的三条线段,能组成三角形的是( )
A.1cm,2cm,4cm B.2cm,3cm,5cm
C.5cm,6cm,12cm D.4cm,6cm,8cm
4.如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是( )
A.80° B.90° C.100° D.110°
5.如图,在△ABC中AB=AC,D是BC的中点,∠B=36°,则∠BAD=( )
A.108° B.72° C.54° D.36°
6.如图,点E,点F在直线AC上,AF=CE,AD=CB,下列条件中不能推断△ADF≌△CBE的是( )
A.∠D=∠B B.∠A=∠C C.BE=DF D.AD∥BC
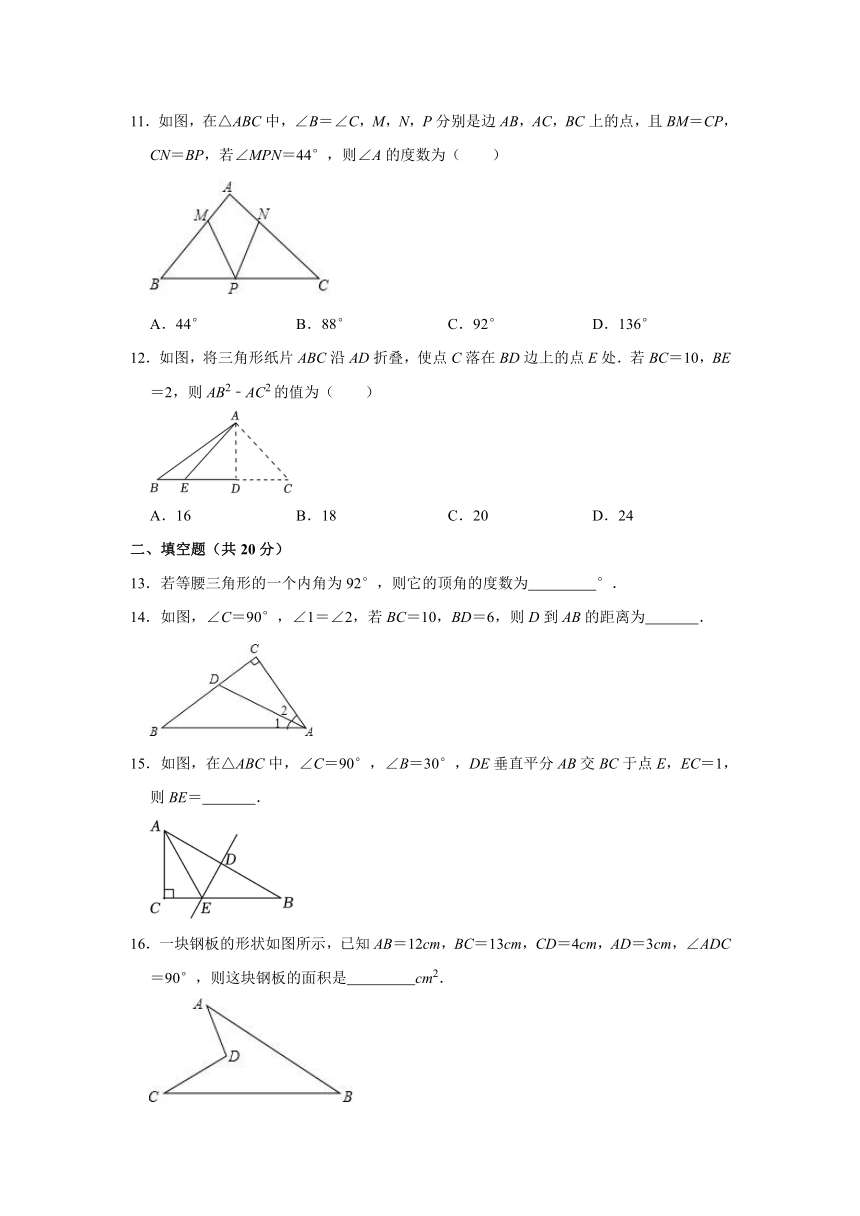
7.如图,在△ABC中,AD是BC边上的高,点E、F是AD上的两点,AB=AC,BC=4,AD=3,则图中阴影部分的面积是( )
A.12 B.6 C.3 D.4
8.如图,△ABC≌△DEC,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.15° B.25° C.35° D.65°
9.如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A.4 B.3 C.2 D.1.5
10.剪纸是我国传统的民间艺术.如图①,②将一张纸片进行两次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A.B.C.D.
11.如图,在△ABC中,∠B=∠C,M,N,P分别是边AB,AC,BC上的点,且BM=CP,CN=BP,若∠MPN=44°,则∠A的度数为( )
A.44° B.88° C.92° D.136°
12.如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=10,BE=2,则AB2﹣AC2的值为( )
A.16 B.18 C.20 D.24
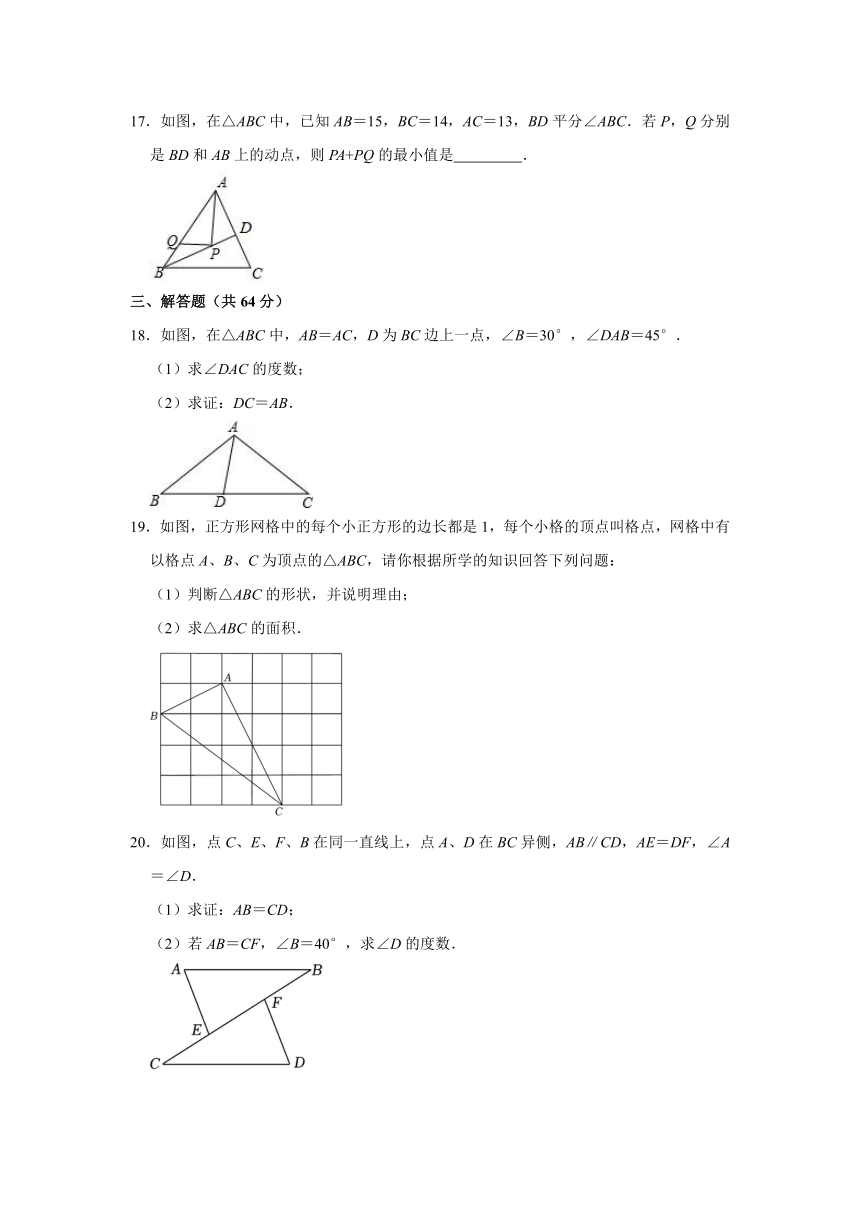
二、填空题(共20分)
13.若等腰三角形的一个内角为92°,则它的顶角的度数为 °.
14.如图,∠C=90°,∠1=∠2,若BC=10,BD=6,则D到AB的距离为 .
15.如图,在△ABC中,∠C=90°,∠B=30°,DE垂直平分AB交BC于点E,EC=1,则BE= .
16.一块钢板的形状如图所示,已知AB=12cm,BC=13cm,CD=4cm,AD=3cm,∠ADC=90°,则这块钢板的面积是 cm2.
17.如图,在△ABC中,已知AB=15,BC=14,AC=13,BD平分∠ABC.若P,Q分别是BD和AB上的动点,则PA+PQ的最小值是 .
三、解答题(共64分)
18.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)求证:DC=AB.
19.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点,网格中有以格点A、B、C为顶点的△ABC,请你根据所学的知识回答下列问题:
(1)判断△ABC的形状,并说明理由;
(2)求△ABC的面积.
20.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
21.如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D.
(1)求∠ADC的度数;
(2)求证:DC=2DB.
22.如图,在等腰△ABC中,AB=AC,BC=5.点D为AC上一点,且BD=4,CD=3.
(1)求证:BD⊥AC;
(2)求AB的长.
23.如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A、B、C都在格点上,
(1)在图中画出与△ABC关于直线l成轴对称的△A1B1C1;
(2)在直线l上找出一点Q,使得|QA+QC|的值最小;(保留作图痕迹并标上字母Q)
(3)在直线l上找出一点P,使得|PA﹣PC|的值最大.(保留作图痕迹并标上字母P)
24.在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,判断BD和CE的数量关系和位置关系,并说明理由;
(2)设∠BAC=α,∠DCE=β.
如图2,当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论.
参考答案
一、选择题(共36分)
1.解:如果一个三角形是轴对称图形,那么这个三角形一定是等腰三角形.
故选:D.
2.解:在△ABC中,AB边上的高线画法正确的是B,
故选:B.
3.解:A、1+2<4,不能构成三角形;
B、2+3=5,不能构成三角形;
C、5+6<12,不能够组成三角形;
D、4+6>8,能构成三角形.
故选:D.
4.解:∵∠A=30°,∠B=50°,
∴∠ACB=180°﹣30°﹣50°=100°(三角形内角和定义).
∵CD平分∠ACB,
∴∠BCD=∠ACB=×100°=50°,
∴∠ADC=∠BCD+∠B=50°+50°=100°.
故选:C.
5.解:∵AB=AC,D是BC的中点,
∴AD⊥BC,
∵∠B=36°,
∴∠BAD=90°﹣36°=54°.
故选:C.
6.解:A、SSA不能判定三角形全等,本选项符合题意.
B、根据SAS,可以推出△ADF≌△CBE,本选项不符合题意.
C、根据SSS,可以推出△ADF≌△CBE,本选项不符合题意.
D、根据SAS,可以推出△ADF≌△CBE,本选项不符合题意.
故选:A.
7.解:∵AB=AC,BC=4,AD是△ABC的中线,
∴BD=DC=BC=2,AD⊥BC,
∴△ABC关于直线AD对称,
∴B、C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF,
∵△ABC的面积是:×BC×AD=×3×4=6,
∴图中阴影部分的面积是S△ABC=3.
故选:C.
8.解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,
∴∠BCE=∠ACD,
∵∠BCE=65°,
∴∠ACD=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF=90°﹣∠ACD=25°,
故选:B.
9.解:∵AD,BE是△ABC的高线,
∴∠ADB=∠ADC=∠AEB=90°,
∵∠BFD=∠AFE,
∴∠DBF=∠CAD,
在△ACD和△BFD中,
,
∴△ACD≌△BFD(ASA),
∴DF=DC,
∵△ACD的面积为12,
∴,
∴CD=4,
∴DF=4,
∴AF=AD﹣DF=2,
故选:C.
10.解:按照图中的顺序,向右对折,向上对折,从斜边处剪去一个直角三角形,从直角顶点处剪去一个直角梯形,展开后实际是从原菱形的四边处各剪去一个直角三角形,从菱形的中心剪去一个六边形,可得:
.
故选:B.
11.解:在△BMP和△CPN中,
,
∴△BMP≌△CPN(SAS),
∴∠BMP=∠CPN,
∵∠MPN=44°,
∴∠BPM+∠CPN=136°,
∴∠BMP+∠BPM=136°,
∴∠B=44°,
∴∠C=∠B=44°,
∴∠A=180°﹣44°﹣44°=92°,
故选:C.
12.解:∵将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处,
∴∠ADC=∠ADE=90°,DE=CD=CE,
∵BC=10,BE=2
∴CE=8,
∴CD=DE=4,BD=6,
在Rt△ABD中,AB2=AD2+BD2,
在Rt△ACD中,AC2=AD2+CD2,
∴AB2﹣AC2=BD2﹣CD2=20,
故选:C.
二、填空题(共20分)
13.解:∵92°>90°,
∴92°的角是顶角,
故答案为:92.
14.解:∵BC=10,BD=6,
∴CD=4,
∵∠C=90°,∠1=∠2,
∴点D到边AB的距离等于CD=4,
故答案为:4.
15.解:∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B=30°,
∴∠AEC=30°+30°=60°,
∴∠CAE=180°﹣90°﹣60°=30°,
∴AE=2CE=2,
∴BE=AE=2.
故答案为:2.
16.解:连接AC,由勾股定理得AC==5cm,
∵AB=12cm,BC=13cm,AC2+AB2=BC2,
即52+122=132,
故△ABC是直角三角形,∠CAB=90°,
故四边形ABCD的面积=S△ABC﹣S△ACD,
=AB AC﹣AD CD,
=×12×5﹣×4×3,
=30﹣6,
=24cm2,
故答案为:24.
17.解:如图,作点Q关于直线BD的对称点Q′,作AM⊥BC于M.
∵PA+PQ=PA+PQ′,
∴根据垂线段最短可知,当A,P,Q′共线,且与AM重合时,PA+PQ的值最小,最小值=线段AM的长.
设CM=x,AM=y,
由题意:,
解得y=12,
∴PA+PQ的最小值为12.
故答案为12.
三、解答题(共64分)
18.(1)解:∵AB=AC,
∴∠C=∠B=30°,
∵∠C+∠BAC+∠B=180°,
∴∠BAC=180°﹣30°﹣30°=120°,
∵∠DAB=45°,
∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°;
(2)证明:∵∠DAB=45°,∠DAC=75°,
∴∠ADC=∠B+∠DAB=30°+45°=75°,
∴∠DAC=∠ADC,
∴DC=AC,
∵AB=AC,
∴DC=AB.
19.解:(1)△ABC是直角三角形,
理由是:由勾股定理得:AB2=12+22=5,AC2=22+42=20,BC2=32+42=25,
所以AB2+AC2=BC2,
即△ABC是直角三角形;
(2)由(1)知:AB=,AC==2,
所以△ABC的面积==×2=5.
20.(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△DCF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFD=(180°﹣40°)=70°.
21.解:(1)∵AB=AC,∠BAC=120°,
∴∠B=(180°﹣∠BAC)=(180°﹣120°)=30°,
∵AB的垂直平分线交BC于点D.
∴AD=BD,
∴∠BAD=∠B=30°,
∴∠ADC=∠B+∠BAD=30°+30°=60°;
(2)∵∠ADC=60°,∠C=30°,
∴∠DAC=90°,
∴AD=CD,∠BAD=30°,
∴∠B=∠BAD,
∴BD=AD,
∴DC=2DB.
22.(1)证明:∵CD=3,BC=5,BD=4,
∴CD2+BD2=9+16=25=BC2,
∴△BCD是直角三角形,
∴BD⊥AC;
(2)解:设AD=x,则AC=x+3.
∵AB=AC,
∴AB=x+3.
∵∠BDC=90°,
∴∠ADB=90°,
∴AB2=AD2+BD2,
即(x+3)2=x2+42,
解得:x=,
∴AB=+3=.
23.解:(1)如图,△A1B1C1即为所求.
(2)如图,点Q即为所求.
(3)如图,点P即为所求.
24.解:(1)BD=CE,BD⊥CE,
理由:∵∠DAE=∠BAC=90°,AB=AC,
∴∠ACB=∠B=45°,∠BAD=∠CAE=90°﹣∠CAD,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠B=∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=90°,
∴BD⊥CE.
(2)α+β=180°,
证明:∵∠DAE=∠BAC=α,
∴∠DAE﹣∠CAD=∠BAC﹣∠CAD,
∴∠CAE=∠BAD,
在△CAE和△BAD中,
,
∴△CAE≌△BAD(SAS),
∴∠ACE=∠B,
∵∠B=∠ACB,
∴∠ACE=∠ACB,
∴∠B+∠ACB=∠ACE+∠ACB=∠DCE=β,
∵∠BAC+∠B+∠ACB=180°,
∴α+β=180°.
一、选择题(共36分)
1.如果一个三角形是轴对称图形,那么这个三角形一定是( )
A.直角三角形 B.等腰直角三角形
C.等边三角形 D.等腰三角形
2.如图所示在△ABC中,AB边上的高线画法正确的是( )
A. B.
C. D.
3.下列长度的三条线段,能组成三角形的是( )
A.1cm,2cm,4cm B.2cm,3cm,5cm
C.5cm,6cm,12cm D.4cm,6cm,8cm
4.如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是( )
A.80° B.90° C.100° D.110°
5.如图,在△ABC中AB=AC,D是BC的中点,∠B=36°,则∠BAD=( )
A.108° B.72° C.54° D.36°
6.如图,点E,点F在直线AC上,AF=CE,AD=CB,下列条件中不能推断△ADF≌△CBE的是( )
A.∠D=∠B B.∠A=∠C C.BE=DF D.AD∥BC
7.如图,在△ABC中,AD是BC边上的高,点E、F是AD上的两点,AB=AC,BC=4,AD=3,则图中阴影部分的面积是( )
A.12 B.6 C.3 D.4
8.如图,△ABC≌△DEC,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.15° B.25° C.35° D.65°
9.如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A.4 B.3 C.2 D.1.5
10.剪纸是我国传统的民间艺术.如图①,②将一张纸片进行两次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A.B.C.D.
11.如图,在△ABC中,∠B=∠C,M,N,P分别是边AB,AC,BC上的点,且BM=CP,CN=BP,若∠MPN=44°,则∠A的度数为( )
A.44° B.88° C.92° D.136°
12.如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=10,BE=2,则AB2﹣AC2的值为( )
A.16 B.18 C.20 D.24
二、填空题(共20分)
13.若等腰三角形的一个内角为92°,则它的顶角的度数为 °.
14.如图,∠C=90°,∠1=∠2,若BC=10,BD=6,则D到AB的距离为 .
15.如图,在△ABC中,∠C=90°,∠B=30°,DE垂直平分AB交BC于点E,EC=1,则BE= .
16.一块钢板的形状如图所示,已知AB=12cm,BC=13cm,CD=4cm,AD=3cm,∠ADC=90°,则这块钢板的面积是 cm2.
17.如图,在△ABC中,已知AB=15,BC=14,AC=13,BD平分∠ABC.若P,Q分别是BD和AB上的动点,则PA+PQ的最小值是 .
三、解答题(共64分)
18.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)求证:DC=AB.
19.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点,网格中有以格点A、B、C为顶点的△ABC,请你根据所学的知识回答下列问题:
(1)判断△ABC的形状,并说明理由;
(2)求△ABC的面积.
20.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
21.如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D.
(1)求∠ADC的度数;
(2)求证:DC=2DB.
22.如图,在等腰△ABC中,AB=AC,BC=5.点D为AC上一点,且BD=4,CD=3.
(1)求证:BD⊥AC;
(2)求AB的长.
23.如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A、B、C都在格点上,
(1)在图中画出与△ABC关于直线l成轴对称的△A1B1C1;
(2)在直线l上找出一点Q,使得|QA+QC|的值最小;(保留作图痕迹并标上字母Q)
(3)在直线l上找出一点P,使得|PA﹣PC|的值最大.(保留作图痕迹并标上字母P)
24.在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,判断BD和CE的数量关系和位置关系,并说明理由;
(2)设∠BAC=α,∠DCE=β.
如图2,当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论.
参考答案
一、选择题(共36分)
1.解:如果一个三角形是轴对称图形,那么这个三角形一定是等腰三角形.
故选:D.
2.解:在△ABC中,AB边上的高线画法正确的是B,
故选:B.
3.解:A、1+2<4,不能构成三角形;
B、2+3=5,不能构成三角形;
C、5+6<12,不能够组成三角形;
D、4+6>8,能构成三角形.
故选:D.
4.解:∵∠A=30°,∠B=50°,
∴∠ACB=180°﹣30°﹣50°=100°(三角形内角和定义).
∵CD平分∠ACB,
∴∠BCD=∠ACB=×100°=50°,
∴∠ADC=∠BCD+∠B=50°+50°=100°.
故选:C.
5.解:∵AB=AC,D是BC的中点,
∴AD⊥BC,
∵∠B=36°,
∴∠BAD=90°﹣36°=54°.
故选:C.
6.解:A、SSA不能判定三角形全等,本选项符合题意.
B、根据SAS,可以推出△ADF≌△CBE,本选项不符合题意.
C、根据SSS,可以推出△ADF≌△CBE,本选项不符合题意.
D、根据SAS,可以推出△ADF≌△CBE,本选项不符合题意.
故选:A.
7.解:∵AB=AC,BC=4,AD是△ABC的中线,
∴BD=DC=BC=2,AD⊥BC,
∴△ABC关于直线AD对称,
∴B、C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF,
∵△ABC的面积是:×BC×AD=×3×4=6,
∴图中阴影部分的面积是S△ABC=3.
故选:C.
8.解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,
∴∠BCE=∠ACD,
∵∠BCE=65°,
∴∠ACD=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF=90°﹣∠ACD=25°,
故选:B.
9.解:∵AD,BE是△ABC的高线,
∴∠ADB=∠ADC=∠AEB=90°,
∵∠BFD=∠AFE,
∴∠DBF=∠CAD,
在△ACD和△BFD中,
,
∴△ACD≌△BFD(ASA),
∴DF=DC,
∵△ACD的面积为12,
∴,
∴CD=4,
∴DF=4,
∴AF=AD﹣DF=2,
故选:C.
10.解:按照图中的顺序,向右对折,向上对折,从斜边处剪去一个直角三角形,从直角顶点处剪去一个直角梯形,展开后实际是从原菱形的四边处各剪去一个直角三角形,从菱形的中心剪去一个六边形,可得:
.
故选:B.
11.解:在△BMP和△CPN中,
,
∴△BMP≌△CPN(SAS),
∴∠BMP=∠CPN,
∵∠MPN=44°,
∴∠BPM+∠CPN=136°,
∴∠BMP+∠BPM=136°,
∴∠B=44°,
∴∠C=∠B=44°,
∴∠A=180°﹣44°﹣44°=92°,
故选:C.
12.解:∵将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处,
∴∠ADC=∠ADE=90°,DE=CD=CE,
∵BC=10,BE=2
∴CE=8,
∴CD=DE=4,BD=6,
在Rt△ABD中,AB2=AD2+BD2,
在Rt△ACD中,AC2=AD2+CD2,
∴AB2﹣AC2=BD2﹣CD2=20,
故选:C.
二、填空题(共20分)
13.解:∵92°>90°,
∴92°的角是顶角,
故答案为:92.
14.解:∵BC=10,BD=6,
∴CD=4,
∵∠C=90°,∠1=∠2,
∴点D到边AB的距离等于CD=4,
故答案为:4.
15.解:∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B=30°,
∴∠AEC=30°+30°=60°,
∴∠CAE=180°﹣90°﹣60°=30°,
∴AE=2CE=2,
∴BE=AE=2.
故答案为:2.
16.解:连接AC,由勾股定理得AC==5cm,
∵AB=12cm,BC=13cm,AC2+AB2=BC2,
即52+122=132,
故△ABC是直角三角形,∠CAB=90°,
故四边形ABCD的面积=S△ABC﹣S△ACD,
=AB AC﹣AD CD,
=×12×5﹣×4×3,
=30﹣6,
=24cm2,
故答案为:24.
17.解:如图,作点Q关于直线BD的对称点Q′,作AM⊥BC于M.
∵PA+PQ=PA+PQ′,
∴根据垂线段最短可知,当A,P,Q′共线,且与AM重合时,PA+PQ的值最小,最小值=线段AM的长.
设CM=x,AM=y,
由题意:,
解得y=12,
∴PA+PQ的最小值为12.
故答案为12.
三、解答题(共64分)
18.(1)解:∵AB=AC,
∴∠C=∠B=30°,
∵∠C+∠BAC+∠B=180°,
∴∠BAC=180°﹣30°﹣30°=120°,
∵∠DAB=45°,
∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°;
(2)证明:∵∠DAB=45°,∠DAC=75°,
∴∠ADC=∠B+∠DAB=30°+45°=75°,
∴∠DAC=∠ADC,
∴DC=AC,
∵AB=AC,
∴DC=AB.
19.解:(1)△ABC是直角三角形,
理由是:由勾股定理得:AB2=12+22=5,AC2=22+42=20,BC2=32+42=25,
所以AB2+AC2=BC2,
即△ABC是直角三角形;
(2)由(1)知:AB=,AC==2,
所以△ABC的面积==×2=5.
20.(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△DCF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFD=(180°﹣40°)=70°.
21.解:(1)∵AB=AC,∠BAC=120°,
∴∠B=(180°﹣∠BAC)=(180°﹣120°)=30°,
∵AB的垂直平分线交BC于点D.
∴AD=BD,
∴∠BAD=∠B=30°,
∴∠ADC=∠B+∠BAD=30°+30°=60°;
(2)∵∠ADC=60°,∠C=30°,
∴∠DAC=90°,
∴AD=CD,∠BAD=30°,
∴∠B=∠BAD,
∴BD=AD,
∴DC=2DB.
22.(1)证明:∵CD=3,BC=5,BD=4,
∴CD2+BD2=9+16=25=BC2,
∴△BCD是直角三角形,
∴BD⊥AC;
(2)解:设AD=x,则AC=x+3.
∵AB=AC,
∴AB=x+3.
∵∠BDC=90°,
∴∠ADB=90°,
∴AB2=AD2+BD2,
即(x+3)2=x2+42,
解得:x=,
∴AB=+3=.
23.解:(1)如图,△A1B1C1即为所求.
(2)如图,点Q即为所求.
(3)如图,点P即为所求.
24.解:(1)BD=CE,BD⊥CE,
理由:∵∠DAE=∠BAC=90°,AB=AC,
∴∠ACB=∠B=45°,∠BAD=∠CAE=90°﹣∠CAD,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠B=∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=90°,
∴BD⊥CE.
(2)α+β=180°,
证明:∵∠DAE=∠BAC=α,
∴∠DAE﹣∠CAD=∠BAC﹣∠CAD,
∴∠CAE=∠BAD,
在△CAE和△BAD中,
,
∴△CAE≌△BAD(SAS),
∴∠ACE=∠B,
∵∠B=∠ACB,
∴∠ACE=∠ACB,
∴∠B+∠ACB=∠ACE+∠ACB=∠DCE=β,
∵∠BAC+∠B+∠ACB=180°,
∴α+β=180°.
