2023—2024学年人教版数学八年级上册12.2三角形全等的判定 同步练习(含答案)
文档属性
| 名称 | 2023—2024学年人教版数学八年级上册12.2三角形全等的判定 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 167.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 20:10:28 | ||
图片预览

文档简介
12.2三角形全等的判定
一、选择题
1.下列说法错误的是( )
A.有两条边和它们的夹角对应相等的两个三角形全等
B.有三个角对应相等的两个三角形全等
C.有两个角及其中一角的对边对应相等的两个三角形全等
D.有三条边对应相等的两个三角形全等
2.下图中的全等三角形是( )
A.①和② B.②和③ C.②和④ D.①和③
3.如图,已知 ,若要使得 ,则添加的一个条件不能是( )
A. B. C.AB=DC D.AC=DB
4.如图, , ,垂足分别为D、E,且 ,则直接判定 与 全等的理由是( )
A.SAS B.AAS C.SSS D.HL
5.如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为( )
A.2 B.2.5 C.3 D.4
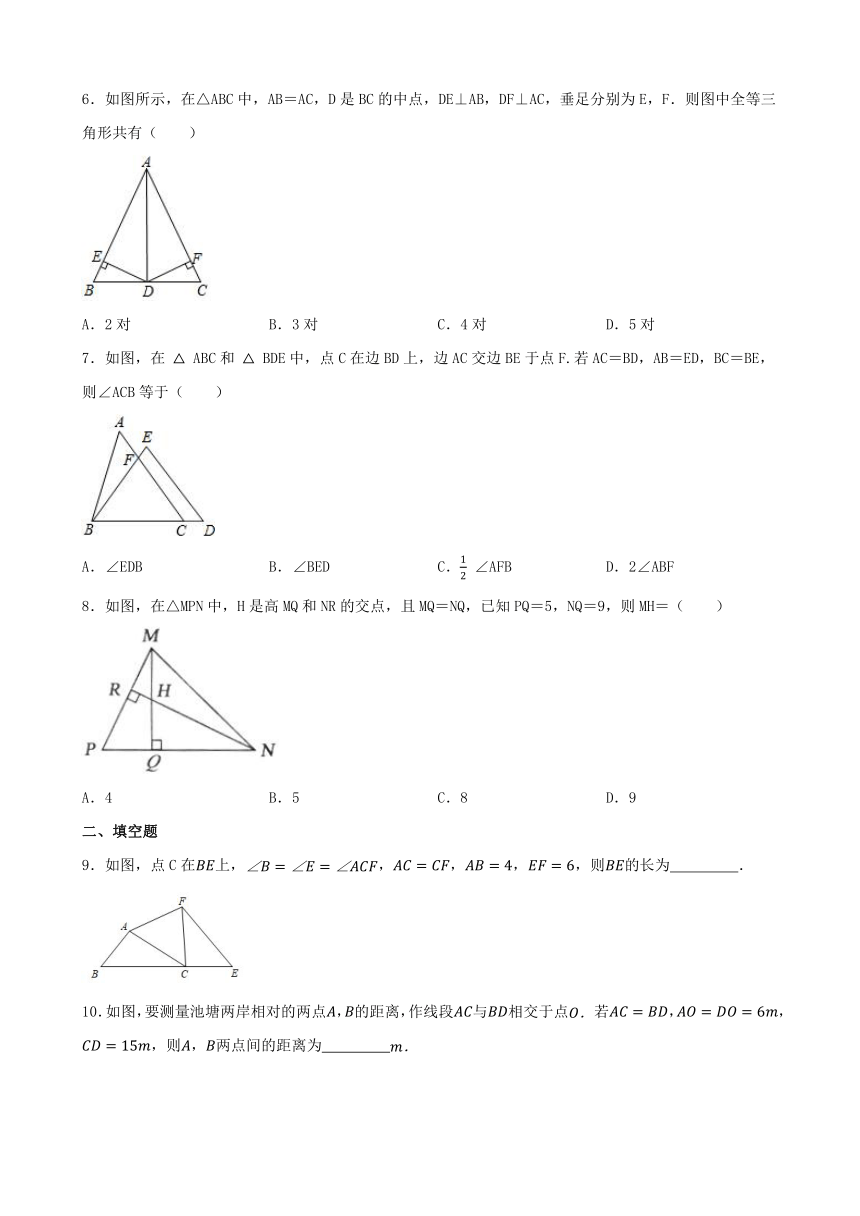
6.如图所示,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E,F.则图中全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
7.如图,在 ABC和 BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
A.∠EDB B.∠BED C. ∠AFB D.2∠ABF
8.如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH=( )
A.4 B.5 C.8 D.9
二、填空题
9.如图,点C在上,,,,,则的长为 .
10.如图,要测量池塘两岸相对的两点,的距离,作线段与相交于点若,,,则,两点间的距离为
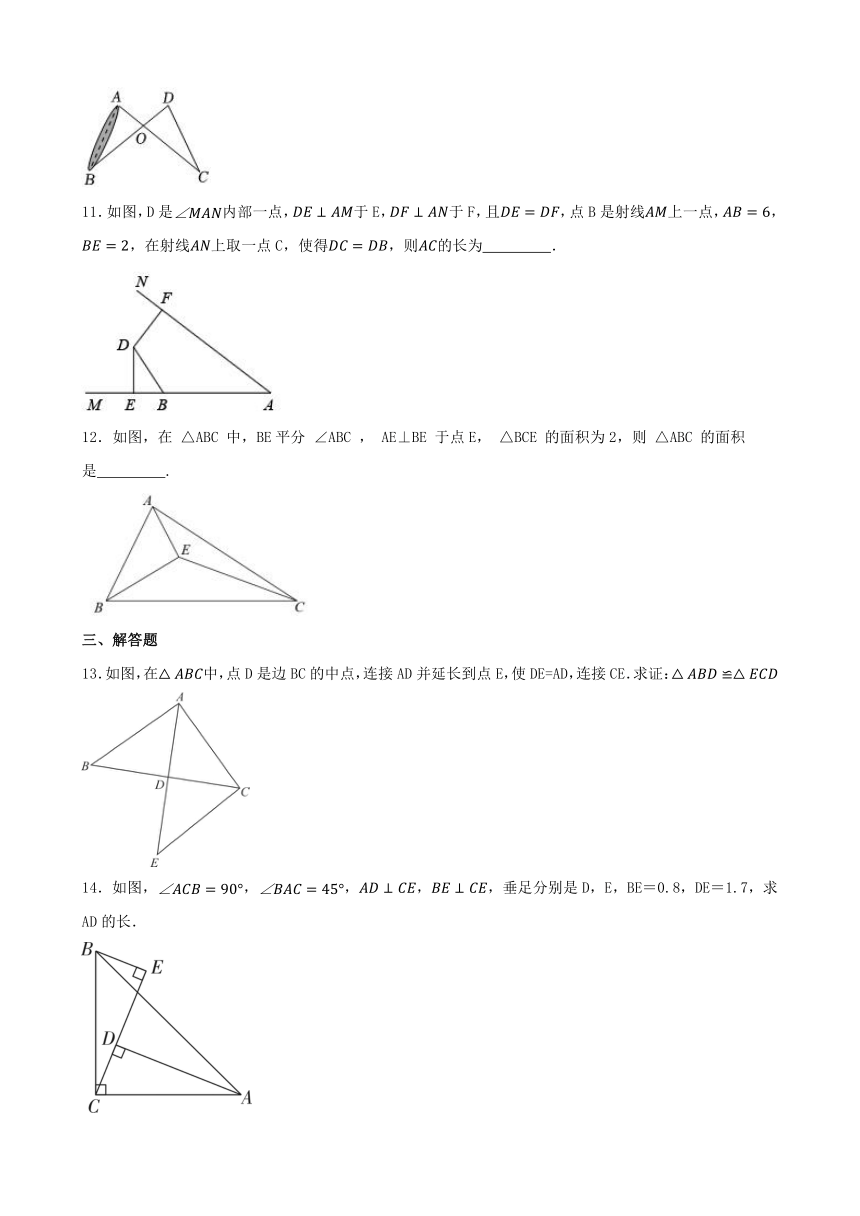
11.如图,D是内部一点,于E,于F,且,点B是射线上一点,,,在射线上取一点C,使得,则的长为 .
12.如图,在 △ABC 中,BE平分 ∠ABC , AE⊥BE 于点E, △BCE 的面积为2,则 △ABC 的面积是 .
三、解答题
13.如图,在中,点D是边BC的中点,连接AD并延长到点E,使DE=AD,连接CE.求证:
14.如图,,,,,垂足分别是D,E,BE=0.8,DE=1.7,求AD的长.
15.如图,在△ABC中,边BC,AB上的高AD,CE相交于点F,且∠ACE=45°,连接BF,求∠BFE的度数.
16.如图,为的高,E为上一点,交于点F,且有,.
(1)求证:;
(2)求的度数.
17.如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.
(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
参考答案
1.B
2.D
3.C
4.D
5.A
6.B
7.C
8.A
9.10
10.15
11.6或10
12.4
13.证明:∵D是BC的中点,
∴BD=CD,
在△ABD与△ECD中,
,
∴△ABD≌△ECD.
14.解:∵,,
∴,
∴,
∵,,
∴,
∴,
∵,
∴
在和中
,
∴,
∴,
15.解:∵AD,CE是边BC,AB上的高,
∴∠AEF=∠BEC=∠CDF=90°,
∵∠ACF=45°,
∴∠EAC=∠ACF=45°,
∴AE=CE,
∵∠DFC=∠EFA,
∴∠EAF=∠BCE,
在△EAF和△ECB中,
∠AEF=∠CEB,AE=CE,∠EAF=∠BCE,
∴△EAF≌△ECB(ASA),
∴EF=BE,
∵∠BEF=90°,
∴∠BFE=45°.
16.(1)证明:∵ 为 的高,
∴ ,
∴ ,
在 和 中,
,
∴ (HL).
(2)解:∵ ,
∴ ,
∵ ,
∴ ,
∴∠ABD的度数是 .
17.证明:(1)∵AB∥CD,∴ ∠BAG=∠G, ∠BAD=∠ADC.
∵AF平分∠BAD,∴∠BAD=2∠BAG=2∠G.
∴∠ADC=∠BAD=2∠G .
∵∠G=29°,∴∠ADC=58°.
(2)∵AF平分∠BAD,∴∠BAG=∠DAG.
∵∠BAG=∠G, ∴∠DAG=∠G.
∴AD=GD.
∵点F是BC的中点,∴BF=CF.
在△ABF和△GCF中,
∵
∴△ABF≌△GCF.
∴AB=GC.
∴AB=GD+CD=AD+CD.
一、选择题
1.下列说法错误的是( )
A.有两条边和它们的夹角对应相等的两个三角形全等
B.有三个角对应相等的两个三角形全等
C.有两个角及其中一角的对边对应相等的两个三角形全等
D.有三条边对应相等的两个三角形全等
2.下图中的全等三角形是( )
A.①和② B.②和③ C.②和④ D.①和③
3.如图,已知 ,若要使得 ,则添加的一个条件不能是( )
A. B. C.AB=DC D.AC=DB
4.如图, , ,垂足分别为D、E,且 ,则直接判定 与 全等的理由是( )
A.SAS B.AAS C.SSS D.HL
5.如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为( )
A.2 B.2.5 C.3 D.4
6.如图所示,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E,F.则图中全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
7.如图,在 ABC和 BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
A.∠EDB B.∠BED C. ∠AFB D.2∠ABF
8.如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH=( )
A.4 B.5 C.8 D.9
二、填空题
9.如图,点C在上,,,,,则的长为 .
10.如图,要测量池塘两岸相对的两点,的距离,作线段与相交于点若,,,则,两点间的距离为
11.如图,D是内部一点,于E,于F,且,点B是射线上一点,,,在射线上取一点C,使得,则的长为 .
12.如图,在 △ABC 中,BE平分 ∠ABC , AE⊥BE 于点E, △BCE 的面积为2,则 △ABC 的面积是 .
三、解答题
13.如图,在中,点D是边BC的中点,连接AD并延长到点E,使DE=AD,连接CE.求证:
14.如图,,,,,垂足分别是D,E,BE=0.8,DE=1.7,求AD的长.
15.如图,在△ABC中,边BC,AB上的高AD,CE相交于点F,且∠ACE=45°,连接BF,求∠BFE的度数.
16.如图,为的高,E为上一点,交于点F,且有,.
(1)求证:;
(2)求的度数.
17.如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.
(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
参考答案
1.B
2.D
3.C
4.D
5.A
6.B
7.C
8.A
9.10
10.15
11.6或10
12.4
13.证明:∵D是BC的中点,
∴BD=CD,
在△ABD与△ECD中,
,
∴△ABD≌△ECD.
14.解:∵,,
∴,
∴,
∵,,
∴,
∴,
∵,
∴
在和中
,
∴,
∴,
15.解:∵AD,CE是边BC,AB上的高,
∴∠AEF=∠BEC=∠CDF=90°,
∵∠ACF=45°,
∴∠EAC=∠ACF=45°,
∴AE=CE,
∵∠DFC=∠EFA,
∴∠EAF=∠BCE,
在△EAF和△ECB中,
∠AEF=∠CEB,AE=CE,∠EAF=∠BCE,
∴△EAF≌△ECB(ASA),
∴EF=BE,
∵∠BEF=90°,
∴∠BFE=45°.
16.(1)证明:∵ 为 的高,
∴ ,
∴ ,
在 和 中,
,
∴ (HL).
(2)解:∵ ,
∴ ,
∵ ,
∴ ,
∴∠ABD的度数是 .
17.证明:(1)∵AB∥CD,∴ ∠BAG=∠G, ∠BAD=∠ADC.
∵AF平分∠BAD,∴∠BAD=2∠BAG=2∠G.
∴∠ADC=∠BAD=2∠G .
∵∠G=29°,∴∠ADC=58°.
(2)∵AF平分∠BAD,∴∠BAG=∠DAG.
∵∠BAG=∠G, ∴∠DAG=∠G.
∴AD=GD.
∵点F是BC的中点,∴BF=CF.
在△ABF和△GCF中,
∵
∴△ABF≌△GCF.
∴AB=GC.
∴AB=GD+CD=AD+CD.
