2023-2024学年度北师大版数学八年级上册 第一章勾股定理检测题(含答案)
文档属性
| 名称 | 2023-2024学年度北师大版数学八年级上册 第一章勾股定理检测题(含答案) | 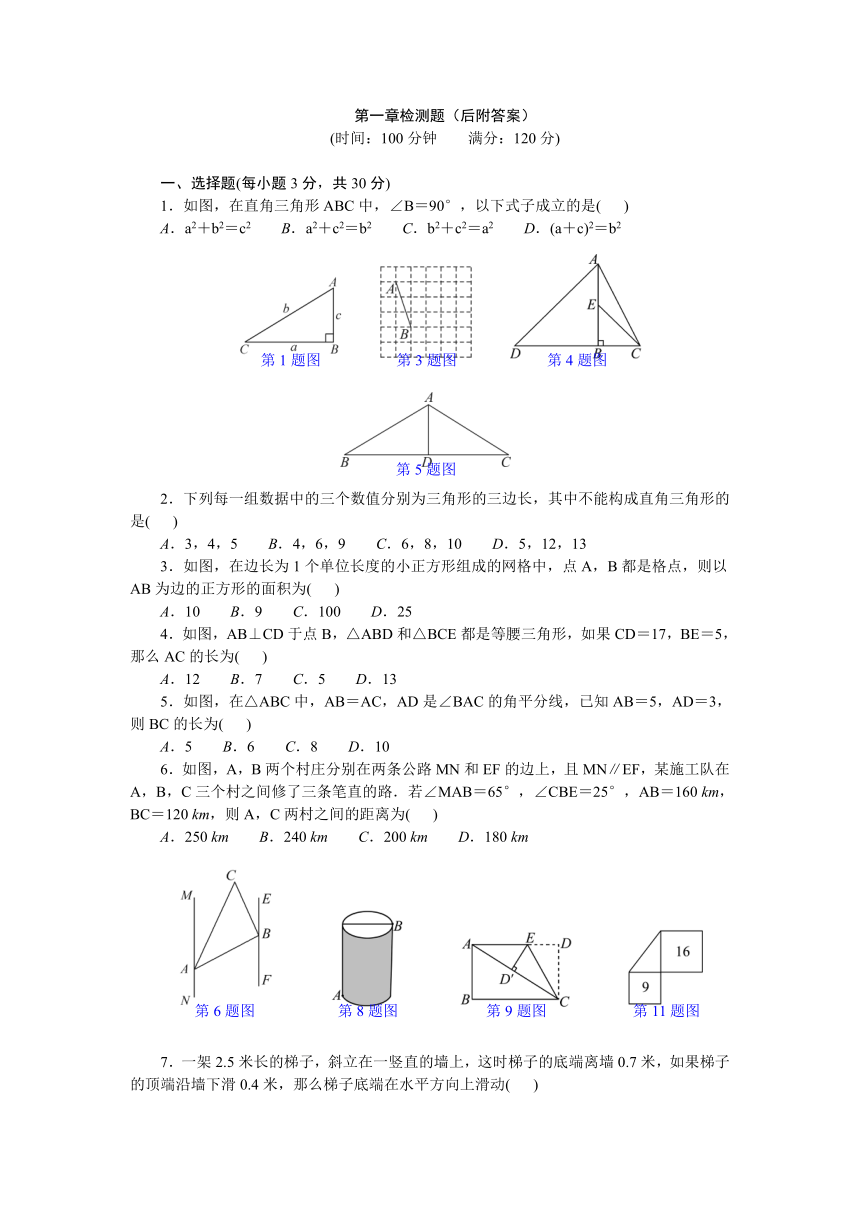 | |
| 格式 | docx | ||
| 文件大小 | 688.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 20:40:14 | ||
图片预览

文档简介
第一章检测题(后附答案)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )
A.a2+b2=c2 B.a2+c2=b2 C.b2+c2=a2 D.(a+c)2=b2
2.下列每一组数据中的三个数值分别为三角形的三边长,其中不能构成直角三角形的是( )
A.3,4,5 B.4,6,9 C.6,8,10 D.5,12,13
3.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则以AB为边的正方形的面积为( )
A.10 B.9 C.100 D.25
4.如图,AB⊥CD于点B,△ABD和△BCE都是等腰三角形,如果CD=17,BE=5,那么AC的长为( )
A.12 B.7 C.5 D.13
5.如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,已知AB=5,AD=3,则BC的长为( )
A.5 B.6 C.8 D.10
6.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160 km,BC=120 km,则A,C两村之间的距离为( )
A.250 km B.240 km C.200 km D.180 km
7.一架2.5米长的梯子,斜立在一竖直的墙上,这时梯子的底端离墙0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯子底端在水平方向上滑动( )
A.0.9米 B.0.8米 C.0.5米 D.0.4米
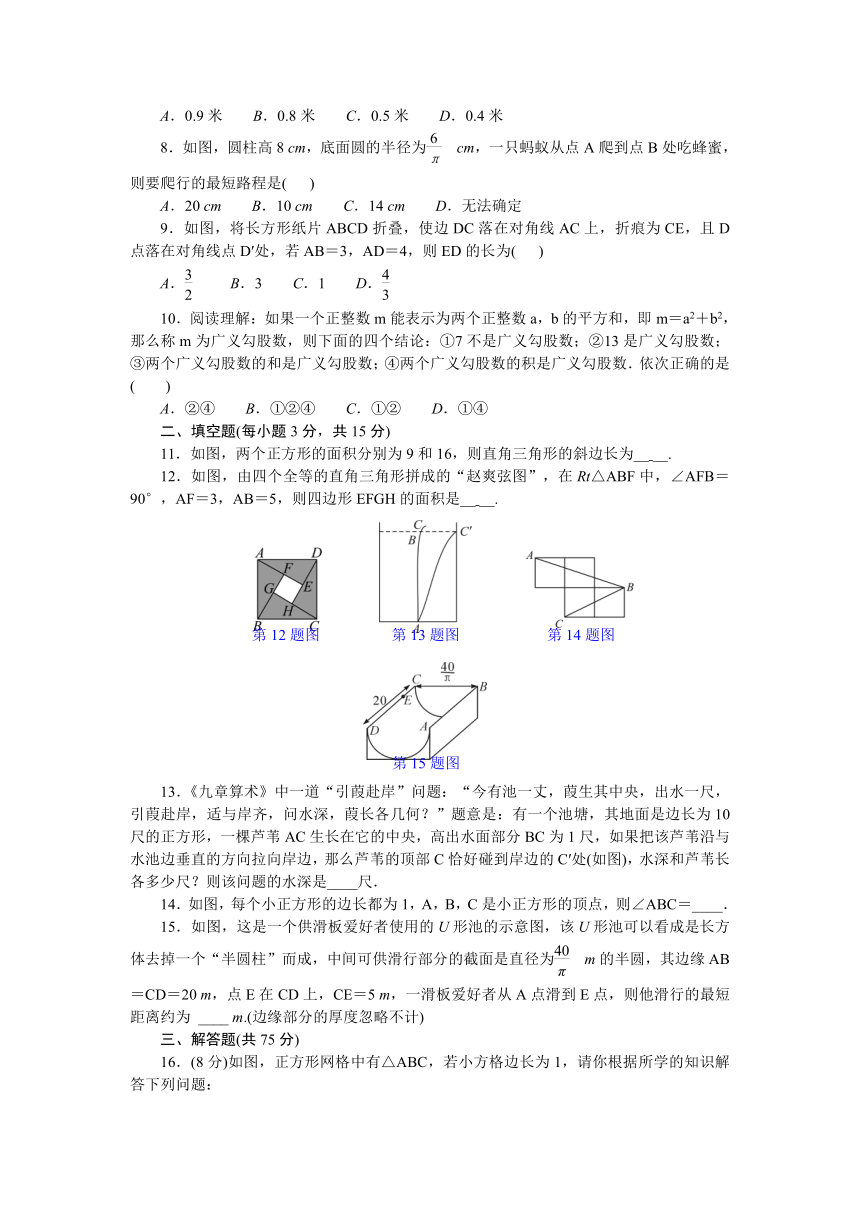
8.如图,圆柱高8 cm,底面圆的半径为 cm,一只蚂蚁从点A爬到点B处吃蜂蜜,则要爬行的最短路程是( )
A.20 cm B.10 cm C.14 cm D.无法确定
9.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线点D′处,若AB=3,AD=4,则ED的长为( )
A. B.3 C.1 D.
10.阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即m=a2+b2,那么称m为广义勾股数,则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是( )
A.②④ B.①②④ C.①② D.①④
二、填空题(每小题3分,共15分)
11.如图,两个正方形的面积分别为9和16,则直角三角形的斜边长为__ __.
12.如图,由四个全等的直角三角形拼成的“赵爽弦图”,在Rt△ABF中,∠AFB=90°,AF=3,AB=5,则四边形EFGH的面积是__ __.
13.《九章算术》中一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C′处(如图),水深和芦苇长各多少尺?则该问题的水深是____尺.
14.如图,每个小正方形的边长都为1,A,B,C是小正方形的顶点,则∠ABC=____.
15.如图,这是一个供滑板爱好者使用的U形池的示意图,该U形池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为 m的半圆,其边缘AB=CD=20 m,点E在CD上,CE=5 m,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为 ____ m.(边缘部分的厚度忽略不计)
三、解答题(共75分)
16.(8分)如图,正方形网格中有△ABC,若小方格边长为1,请你根据所学的知识解答下列问题:
(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
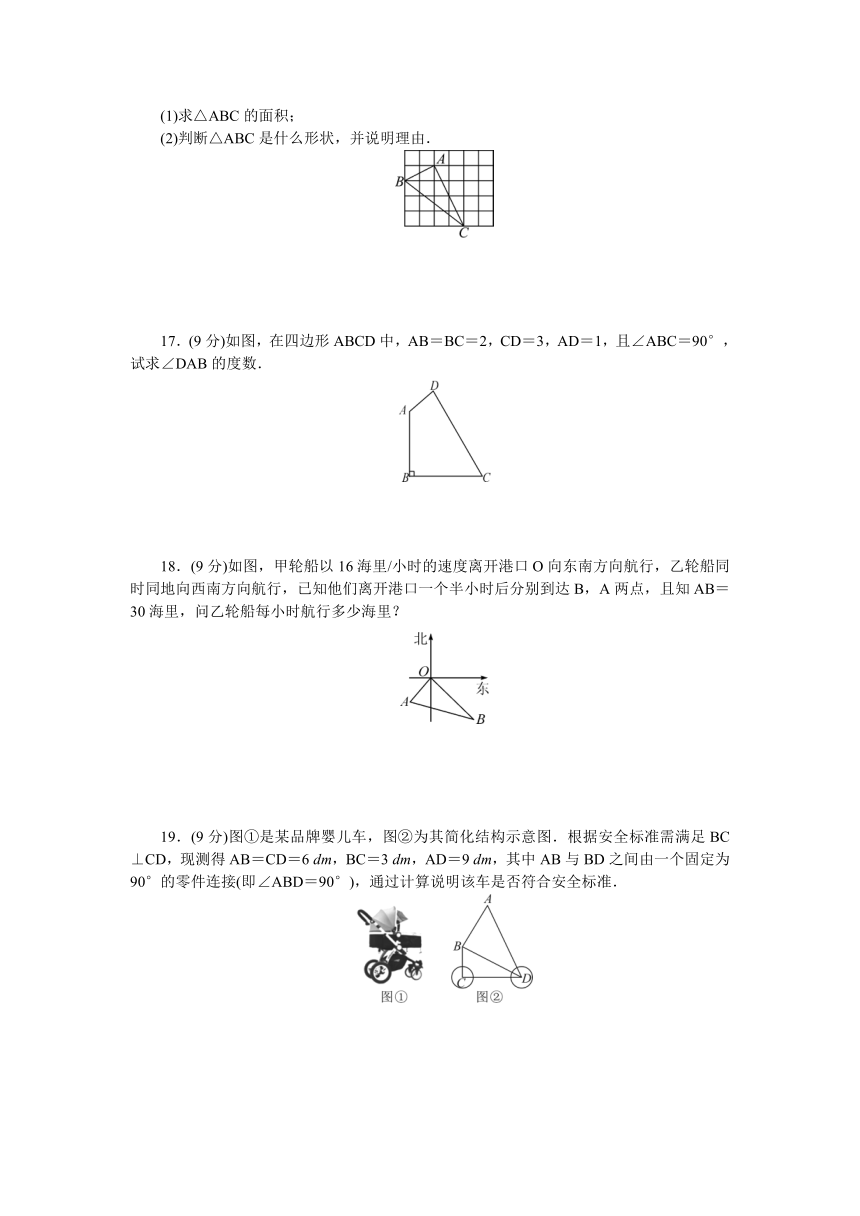
17.(9分)如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且∠ABC=90°,试求∠DAB的度数.
18.(9分)如图,甲轮船以16海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地向西南方向航行,已知他们离开港口一个半小时后分别到达B,A两点,且知AB=30海里,问乙轮船每小时航行多少海里?
19.(9分)图①是某品牌婴儿车,图②为其简化结构示意图.根据安全标准需满足BC⊥CD,现测得AB=CD=6 dm,BC=3 dm,AD=9 dm,其中AB与BD之间由一个固定为90°的零件连接(即∠ABD=90°),通过计算说明该车是否符合安全标准.
20.(9分)学校要征收一块土地,形状如图所示,已知∠B=∠D=90°,AB=20 m,BC=15 m,CD=7 m,土地价格为1000元/m2,请你计算学校征收这块地需用多少元?
21.(10分)如图,在△ABC中,AC=21,BC=13,点D是AC边上一点,BD=12,AD=16.
(1)求证:BD⊥AC;
(2)若点E是AB边上的动点,连接DE,求线段DE的最小值.
22.(10分)如图,在长方形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD.
(1)试说明DG=EP;
(2)求AP的长.
23. (11分)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图①),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)①如图④,⑤,⑥,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3的有__ __个;
②如图⑦所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为S1,S2,直角三角形面积为S3,请判断S1,S2,S3的关系并证明;
(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图⑧所示的“勾股树”.在如图⑨所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知∠1=∠2=∠3=∠α,则当∠α变化时,a2+b2+c2+d2=__ __.(结果可用含m的式子表示)
答案:
第一章检测题
(时间:100分钟 满分:120分)
1.( B )
2.( B )
3.( A )
4.( D )
5.( C )
6.( C )
7.( B )
8.( B )
9.( A )
10.( C )
11.__5__.
12.__1__.
13.__12__尺.
14.则∠ABC=__45°__.
15.__25__ m.(边缘部分的厚度忽略不计)
16.
解:(1)S△ABC=4×4-×1×2-×4×3-×2×4=16-1-6-4=5,所以△ABC的面积为5
(2)△ABC是直角三角形.理由如下:因为AB2=12+22=5,AC2=22+42=20,BC2=32+42=25,所以AC2+AB2=BC2,所以△ABC是直角三角形
17.
解:连接AC,在Rt△ABC中,∵AB=BC,∴∠BAC=∠BCA=45°,由勾股定理,得AC2=AB2+BC2=22+22=8,在△ADC中,AC2+AD2=8+1=9=CD2,所以△ADC是直角三角形,∠DAC=90°,所以∠DAB=∠BAC+∠DAC=90°+45°=135°
18.
解:甲轮船向东南方向航行,乙轮船向西南方向航行,所以AO⊥BO,因为甲轮船以16海里/小时的速度航行了一个半小时,所以OB=16×1.5=24(海里),又因为AB=30海里,所以在Rt△AOB中,AO2=AB2-OB2=324,所以AO=18海里,所以乙轮船每小时航行18÷1.5=12(海里)
19.解:在Rt△ABD中,BD2=AD2-AB2=92-62=45,在△BCD中,BC2+CD2=32+62=45,∴BC2+CD2=BD2,∴△BCD是直角三角形,∠BCD=90°,即BC⊥CD,故该车符合安全标准
20.
解:连接AC.在△ABC中,∠B=90°,AB=20,BC=15,由勾股定理,得AC2=AB2+BC2=202+152=625.在△ADC中,∠D=90°,CD=7,由勾股定理,得AD2=AC2-CD2=625-72=576,所以AD=24.所以S四边形ABCD=S△ABC+S△ACD=AB·BC+CD·AD=234 (m2),234×1000=234000(元).答:学校征收这块地需用234000元
21.
解:(1)∵AC=21,AD=16,∴CD=AC-AD=5,∵BD2+CD2=122+52=169=BC2,∴△BDC是直角三角形,∠BDC=90°,即BD⊥AC
(2)当DE⊥AB时,DE最短.∵AD=16,BD=12,BD⊥AC,∴由勾股定理可得AB=20,∵S△ABD=AD·DB=AB·DE,∴DE==9.6,∴线段DE的最小值为9.6
22.
解:(1)因为四边形ABCD是长方形,所以∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8.由折叠的性质可知EP=AP,BE=AB=8,∠E=∠A=90°,所以∠E=∠D.在△ODP和△OEG中,所以△ODP≌△OEG,所以OP=OG,PD=GE,所以DO+OG=PO+OE,所以DG=EP (2)设AP=EP=DG=x,则GE=PD=AD-AP=6-x,所以CG=DC-DG=8-x,BG=BE-GE=8-(6-x)=2+x.在Rt△CGB中,由勾股定理得BC2+CG2=BG2,即62+(8-x)2=(x+2)2,解得x=4.8,所以AP=4.8
23.
(2)①__3__个;
解:(1)①如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2(或者:在直角三角形中,两条直角边的平方和等于斜边的平方) ②证明:在图①中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和.即c2=ab×4+(b-a)2,化简,得a2+b2=c2.在图②中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和.即(a+b)2=c2+ab×4,化简,得a2+b2=c2.在图③中,梯形的面积等于三个直角三角形的面积的和.即(a+b)(a+b)=ab×2+c2,化简,得a2+b2=c2 (2)①三个图形中面积关系满足S1+S2=S3的有图④,⑤,⑥3个;故答案为:3 ②S1+S2=S3.证明如下:∵S1+S2=π()2+π()2+S3-π()2=π(a2+b2-c2)+S3,∵a2+b2=c2.∴S1+S2=S3 (3)m2
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )
A.a2+b2=c2 B.a2+c2=b2 C.b2+c2=a2 D.(a+c)2=b2
2.下列每一组数据中的三个数值分别为三角形的三边长,其中不能构成直角三角形的是( )
A.3,4,5 B.4,6,9 C.6,8,10 D.5,12,13
3.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则以AB为边的正方形的面积为( )
A.10 B.9 C.100 D.25
4.如图,AB⊥CD于点B,△ABD和△BCE都是等腰三角形,如果CD=17,BE=5,那么AC的长为( )
A.12 B.7 C.5 D.13
5.如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,已知AB=5,AD=3,则BC的长为( )
A.5 B.6 C.8 D.10
6.如图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160 km,BC=120 km,则A,C两村之间的距离为( )
A.250 km B.240 km C.200 km D.180 km
7.一架2.5米长的梯子,斜立在一竖直的墙上,这时梯子的底端离墙0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯子底端在水平方向上滑动( )
A.0.9米 B.0.8米 C.0.5米 D.0.4米
8.如图,圆柱高8 cm,底面圆的半径为 cm,一只蚂蚁从点A爬到点B处吃蜂蜜,则要爬行的最短路程是( )
A.20 cm B.10 cm C.14 cm D.无法确定
9.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线点D′处,若AB=3,AD=4,则ED的长为( )
A. B.3 C.1 D.
10.阅读理解:如果一个正整数m能表示为两个正整数a,b的平方和,即m=a2+b2,那么称m为广义勾股数,则下面的四个结论:①7不是广义勾股数;②13是广义勾股数;③两个广义勾股数的和是广义勾股数;④两个广义勾股数的积是广义勾股数.依次正确的是( )
A.②④ B.①②④ C.①② D.①④
二、填空题(每小题3分,共15分)
11.如图,两个正方形的面积分别为9和16,则直角三角形的斜边长为__ __.
12.如图,由四个全等的直角三角形拼成的“赵爽弦图”,在Rt△ABF中,∠AFB=90°,AF=3,AB=5,则四边形EFGH的面积是__ __.
13.《九章算术》中一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C′处(如图),水深和芦苇长各多少尺?则该问题的水深是____尺.
14.如图,每个小正方形的边长都为1,A,B,C是小正方形的顶点,则∠ABC=____.
15.如图,这是一个供滑板爱好者使用的U形池的示意图,该U形池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为 m的半圆,其边缘AB=CD=20 m,点E在CD上,CE=5 m,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为 ____ m.(边缘部分的厚度忽略不计)
三、解答题(共75分)
16.(8分)如图,正方形网格中有△ABC,若小方格边长为1,请你根据所学的知识解答下列问题:
(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
17.(9分)如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且∠ABC=90°,试求∠DAB的度数.
18.(9分)如图,甲轮船以16海里/小时的速度离开港口O向东南方向航行,乙轮船同时同地向西南方向航行,已知他们离开港口一个半小时后分别到达B,A两点,且知AB=30海里,问乙轮船每小时航行多少海里?
19.(9分)图①是某品牌婴儿车,图②为其简化结构示意图.根据安全标准需满足BC⊥CD,现测得AB=CD=6 dm,BC=3 dm,AD=9 dm,其中AB与BD之间由一个固定为90°的零件连接(即∠ABD=90°),通过计算说明该车是否符合安全标准.
20.(9分)学校要征收一块土地,形状如图所示,已知∠B=∠D=90°,AB=20 m,BC=15 m,CD=7 m,土地价格为1000元/m2,请你计算学校征收这块地需用多少元?
21.(10分)如图,在△ABC中,AC=21,BC=13,点D是AC边上一点,BD=12,AD=16.
(1)求证:BD⊥AC;
(2)若点E是AB边上的动点,连接DE,求线段DE的最小值.
22.(10分)如图,在长方形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD.
(1)试说明DG=EP;
(2)求AP的长.
23. (11分)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图①),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)①如图④,⑤,⑥,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3的有__ __个;
②如图⑦所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为S1,S2,直角三角形面积为S3,请判断S1,S2,S3的关系并证明;
(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图⑧所示的“勾股树”.在如图⑨所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知∠1=∠2=∠3=∠α,则当∠α变化时,a2+b2+c2+d2=__ __.(结果可用含m的式子表示)
答案:
第一章检测题
(时间:100分钟 满分:120分)
1.( B )
2.( B )
3.( A )
4.( D )
5.( C )
6.( C )
7.( B )
8.( B )
9.( A )
10.( C )
11.__5__.
12.__1__.
13.__12__尺.
14.则∠ABC=__45°__.
15.__25__ m.(边缘部分的厚度忽略不计)
16.
解:(1)S△ABC=4×4-×1×2-×4×3-×2×4=16-1-6-4=5,所以△ABC的面积为5
(2)△ABC是直角三角形.理由如下:因为AB2=12+22=5,AC2=22+42=20,BC2=32+42=25,所以AC2+AB2=BC2,所以△ABC是直角三角形
17.
解:连接AC,在Rt△ABC中,∵AB=BC,∴∠BAC=∠BCA=45°,由勾股定理,得AC2=AB2+BC2=22+22=8,在△ADC中,AC2+AD2=8+1=9=CD2,所以△ADC是直角三角形,∠DAC=90°,所以∠DAB=∠BAC+∠DAC=90°+45°=135°
18.
解:甲轮船向东南方向航行,乙轮船向西南方向航行,所以AO⊥BO,因为甲轮船以16海里/小时的速度航行了一个半小时,所以OB=16×1.5=24(海里),又因为AB=30海里,所以在Rt△AOB中,AO2=AB2-OB2=324,所以AO=18海里,所以乙轮船每小时航行18÷1.5=12(海里)
19.解:在Rt△ABD中,BD2=AD2-AB2=92-62=45,在△BCD中,BC2+CD2=32+62=45,∴BC2+CD2=BD2,∴△BCD是直角三角形,∠BCD=90°,即BC⊥CD,故该车符合安全标准
20.
解:连接AC.在△ABC中,∠B=90°,AB=20,BC=15,由勾股定理,得AC2=AB2+BC2=202+152=625.在△ADC中,∠D=90°,CD=7,由勾股定理,得AD2=AC2-CD2=625-72=576,所以AD=24.所以S四边形ABCD=S△ABC+S△ACD=AB·BC+CD·AD=234 (m2),234×1000=234000(元).答:学校征收这块地需用234000元
21.
解:(1)∵AC=21,AD=16,∴CD=AC-AD=5,∵BD2+CD2=122+52=169=BC2,∴△BDC是直角三角形,∠BDC=90°,即BD⊥AC
(2)当DE⊥AB时,DE最短.∵AD=16,BD=12,BD⊥AC,∴由勾股定理可得AB=20,∵S△ABD=AD·DB=AB·DE,∴DE==9.6,∴线段DE的最小值为9.6
22.
解:(1)因为四边形ABCD是长方形,所以∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8.由折叠的性质可知EP=AP,BE=AB=8,∠E=∠A=90°,所以∠E=∠D.在△ODP和△OEG中,所以△ODP≌△OEG,所以OP=OG,PD=GE,所以DO+OG=PO+OE,所以DG=EP (2)设AP=EP=DG=x,则GE=PD=AD-AP=6-x,所以CG=DC-DG=8-x,BG=BE-GE=8-(6-x)=2+x.在Rt△CGB中,由勾股定理得BC2+CG2=BG2,即62+(8-x)2=(x+2)2,解得x=4.8,所以AP=4.8
23.
(2)①__3__个;
解:(1)①如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2(或者:在直角三角形中,两条直角边的平方和等于斜边的平方) ②证明:在图①中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和.即c2=ab×4+(b-a)2,化简,得a2+b2=c2.在图②中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和.即(a+b)2=c2+ab×4,化简,得a2+b2=c2.在图③中,梯形的面积等于三个直角三角形的面积的和.即(a+b)(a+b)=ab×2+c2,化简,得a2+b2=c2 (2)①三个图形中面积关系满足S1+S2=S3的有图④,⑤,⑥3个;故答案为:3 ②S1+S2=S3.证明如下:∵S1+S2=π()2+π()2+S3-π()2=π(a2+b2-c2)+S3,∵a2+b2=c2.∴S1+S2=S3 (3)m2
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
