第三章 位置与坐标单元测试卷(含答案)
文档属性
| 名称 | 第三章 位置与坐标单元测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024北师版八年级数学上学期单元测试卷
第三章 位置与坐标
时间:60分钟 满分:100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·广东深圳龙华区期末)家长会前,四个孩子分别向家长描述自己在班里的座位,家长能准确找到自己孩子座位的是 ( )
A.小明说他坐在第1排
B.小白说他坐在第3列
C.小清说她坐在第2排第5列
D.小楚说他的座位靠窗
2.(2021·四川成都郫都区期末)如图,小手盖住的点的坐标可能为 ( )
A.(5,2) B.(-6,3)
C.(-3,-2) D.(3,-3)
3.(2022·广西百色期中)在图中,所画的平面直角坐标系正确的是 ( )
A B
C D
4.(2022·黑龙江哈尔滨道里区期末)在平面直角坐标系中,点A在y轴上,位于原点上方,距离原点2个单位长度,则点A的坐标为 ( )
A.(2,0) B.(-2,0)
C.(0,2) D.(0,-2)
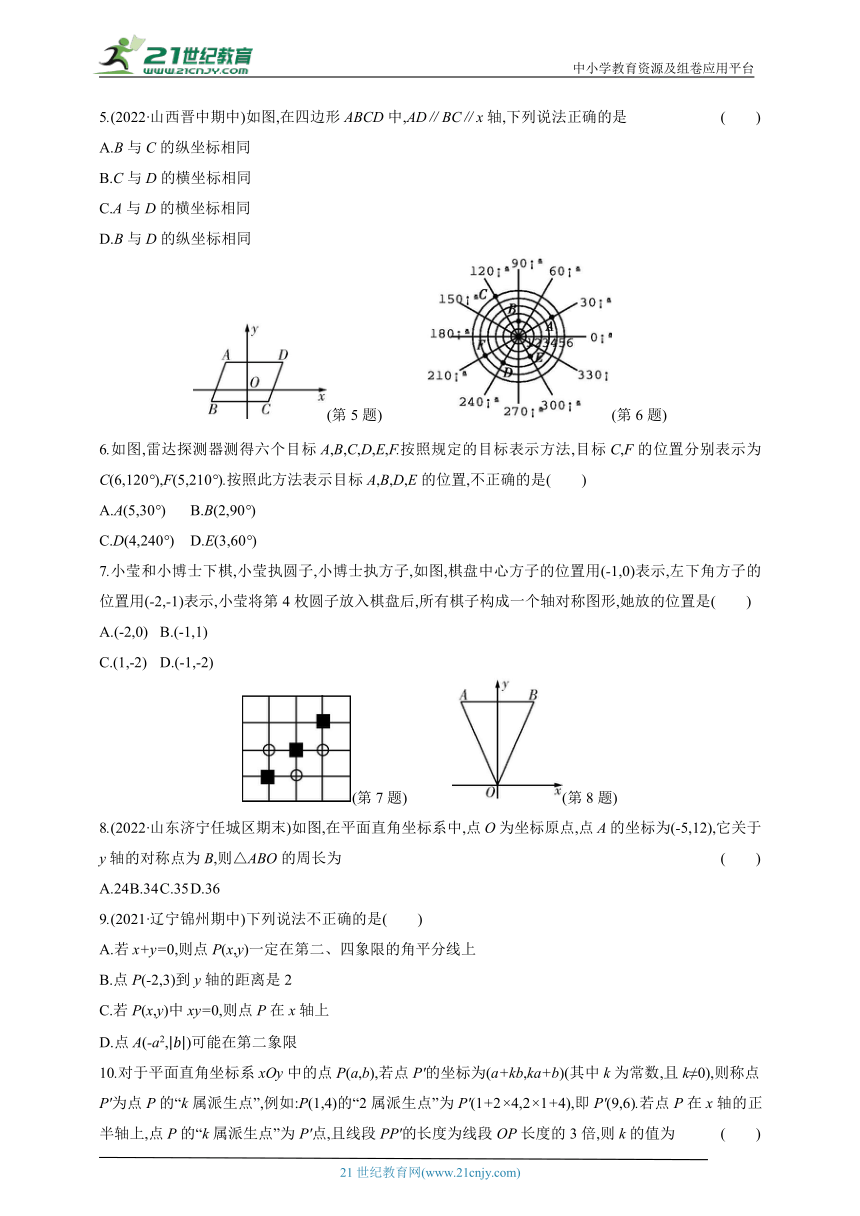
5.(2022·山西晋中期中)如图,在四边形ABCD中,AD∥BC∥x轴,下列说法正确的是 ( )
A.B与C的纵坐标相同
B.C与D的横坐标相同
C.A与D的横坐标相同
D.B与D的纵坐标相同
(第5题) (第6题)
6.如图,雷达探测器测得六个目标A,B,C,D,E,F.按照规定的目标表示方法,目标C,F的位置分别表示为C(6,120°),F(5,210°).按照此方法表示目标A,B,D,E的位置,不正确的是( )
A.A(5,30°) B.B(2,90°)
C.D(4,240°) D.E(3,60°)
7.小莹和小博士下棋,小莹执圆子,小博士执方子,如图,棋盘中心方子的位置用(-1,0)表示,左下角方子的位置用(-2,-1)表示,小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,她放的位置是( )
A.(-2,0) B.(-1,1)
C.(1,-2) D.(-1,-2)
(第7题) (第8题)
8.(2022·山东济宁任城区期末)如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(-5,12),它关于y轴的对称点为B,则△ABO的周长为 ( )
A.24 B.34 C.35 D.36
9.(2021·辽宁锦州期中)下列说法不正确的是( )
A.若x+y=0,则点P(x,y)一定在第二、四象限的角平分线上
B.点P(-2,3)到y轴的距离是2
C.若P(x,y)中xy=0,则点P在x轴上
D.点A(-a2,)可能在第二象限
10.对于平面直角坐标系xOy中的点P(a,b),若点P'的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P'为点P的“k属派生点”,例如:P(1,4)的“2属派生点”为P'(1+2×4,2×1+4),即P'(9,6).若点P在x轴的正半轴上,点P的“k属派生点”为P'点,且线段PP'的长度为线段OP长度的3倍,则k的值为 ( )
A.3 B.±3 C.6 D.±6
二、填空题(共5小题,每小题3分,共15分)
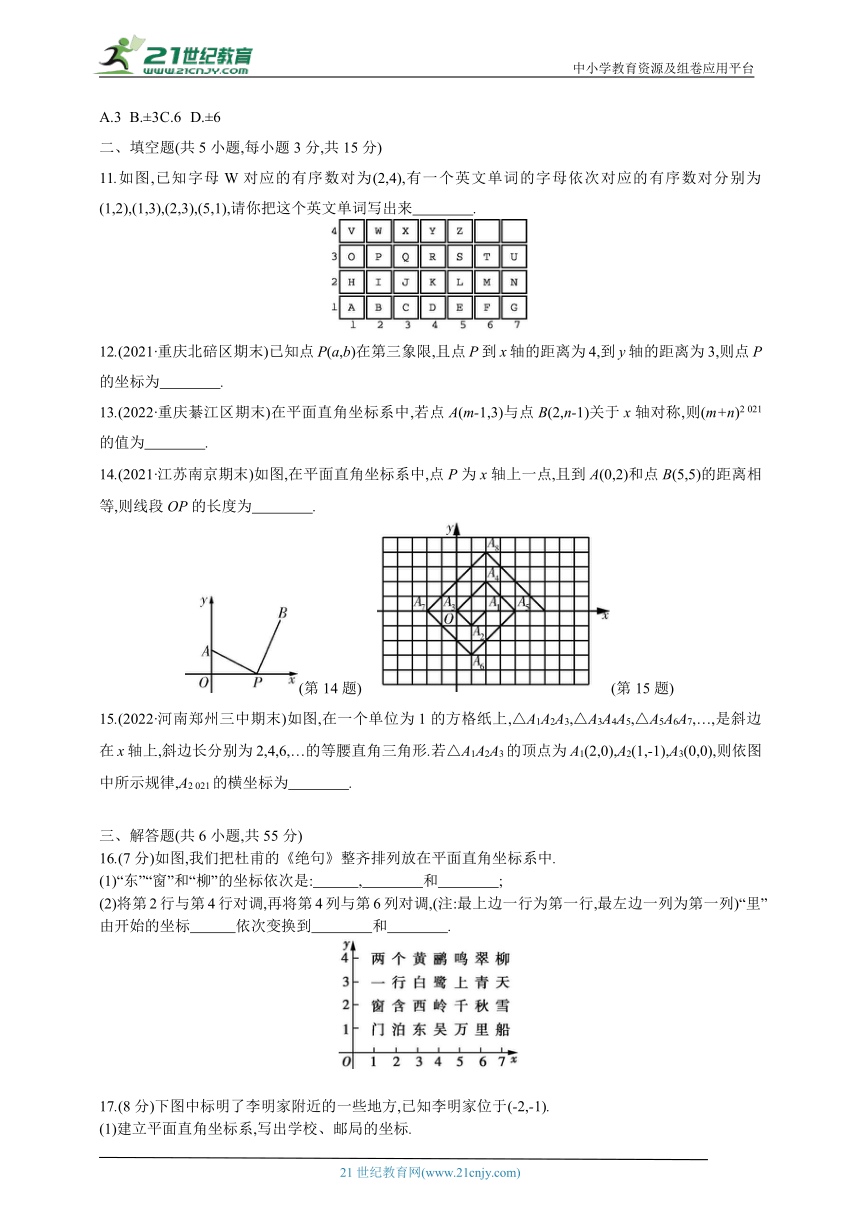
11.如图,已知字母W对应的有序数对为(2,4),有一个英文单词的字母依次对应的有序数对分别为(1,2),(1,3),(2,3),(5,1),请你把这个英文单词写出来 .
12.(2021·重庆北碚区期末)已知点P(a,b)在第三象限,且点P到x轴的距离为4,到y轴的距离为3,则点P的坐标为 .
13.(2022·重庆綦江区期末)在平面直角坐标系中,若点A(m-1,3)与点B(2,n-1)关于x轴对称,则(m+n)2 021的值为 .
14.(2021·江苏南京期末)如图,在平面直角坐标系中,点P为x轴上一点,且到A(0,2)和点B(5,5)的距离相等,则线段OP的长度为 .
(第14题) (第15题)
15.(2022·河南郑州三中期末)如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2 021的横坐标为 .
三、解答题(共6小题,共55分)
16.(7分)如图,我们把杜甫的《绝句》整齐排列放在平面直角坐标系中.
(1)“东”“窗”和“柳”的坐标依次是: , 和 ;
(2)将第2行与第4行对调,再将第4列与第6列对调,(注:最上边一行为第一行,最左边一列为第一列)“里”由开始的坐标 依次变换到 和 .
17.(8分)下图中标明了李明家附近的一些地方,已知李明家位于(-2,-1).
(1)建立平面直角坐标系,写出学校、邮局的坐标.
(2)某星期日早晨,李明从家里出发,沿着(-1,-2),(1,-2),(2,-1),(1,-1),(1,3),(-1,0),(0,-1)的路线转了一下后回到家里,用线段顺次连接李明家和他在路上经过的地点,你能得到什么图形
18.(8分)(2022·浙江宁波期末改编)已知点P(-3a-4,2+a),解答下列问题:
(1)若点P在x轴上,试求出点P的坐标;
(2)若Q(5,8),且PQ∥y轴,试求出点P的坐标.
19.(9分)(2022·河南郑州八中期末)如图,在平面直角坐标内,点A的坐标为(-4,0),点C与点A关于y轴对称.
(1)请在图中标出点A和点C;
(2)求△ABC的面积;
(3)在y轴上有一点D,且S△ACD=S△ABC,写出点D的坐标.
20.(11分)(2021·山东济南期中)如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a,b满足+|b-6|=0,点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着O—C—B—A—O的线路移动一圈停止.
(1)a= ,b= ,点B的坐标为 ;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
21.(12分)(2022·甘肃白银期末)阅读下列文字,然后回答问题.
已知在平面内有两点P1(x1,y1),P2(x2,y2),它们之间的距离P1P2=.
(1)已知A(2,4),B(-3,-8),试求A,B两点间的距离.
(2)已知△DEF各顶点为D(1,6),E(-2,2),F(4,2),请判断此三角形的形状,并说明理由.
(3)在(2)的条件下,在平面直角坐标系中的x轴上找一点P,使PD+PF的长度最短,求出PD+PF的最短长度.
第三章 位置与坐标
1 2 3 4 5 6 7 8 9 10
C D A C A D B D C B
11.HOPE 12.(-3,4) 13.1
14.4.6 15.1 012
1.C (排除法)小明说他坐在第1排,无法确定座位位置;小白说他坐在第3列,无法确定座位位置;小楚说他的座位靠窗,无法确定座位位置.故选C.
2.D
3.A
4.C ∵在平面直角坐标系中,点A在y轴上,位于原点上方,距离原点2个单位长度,∴A点的坐标是(0,2).
5.A ∵在四边形ABCD中,AD∥BC∥x轴,∴点A与D的纵坐标相同,点B与C的纵坐标相同.
6.D
7.B 棋盘中心方子的位置用(-1,0)表示,则这点所在的横线是x轴,这点向右1个单位所在的纵线是y轴,所以建立平面直角坐标系如图,故小莹将第4枚圆子放的位置是(-1,1)时所有棋子构成轴对称图形.
8.D ∵点A与点B关于y轴对称,A(-5,12),∴B(5,12),∴AB=10,OA=13,OB=13,∴△AOB的周长=OA+OB+AB=13+13+10=36.
9.C ∵x+y=0,∴x=-y,即点在第二、四象限的角平分线上;∵点P的横坐标是-2,∴点P到y轴的距离是2;若P(x,y)中xy=0,则点P可能在x轴上,也可能在y轴上;∵-a2≤0,|b|≥0,∴点A可能在第二象限,也可能在坐标轴上.故选C.
10.B ∵点P在x轴的正半轴上,∴P点的纵坐标为0,设P(a,0),a>0,则点P的“k属派生点”P'点为(a,ka),∴PP'=|ka|,OP=|a|,∵线段PP'的长度为线段OP长度的3倍,∴|ka|=3|a|,∴k=±3.
11.HOPE 由题意知(1,2)表示H,(1,3)表示O,(2,3)表示P,(5,1)表示E,所以这个英文单词为HOPE.
12.(-3,4)
13.1 ∵点A(m-1,3)与点B(2,n-1)关于x轴对称,∴m-1=2,n-1=-3,∴m=3,n=-2,∴(m+n)2 021=(3-2)2 021=1.
14.4.6 设点P(x,0),根据题意得x2+22=(5-x)2+52,解得x=4.6,∴OP=4.6.
15.1 012 ∵A3是第一与第二个等腰直角三角形的公共点,A5是第二与第三个等腰直角三角形的公共点,A7是第三与第四个等腰直角三角形的公共点,A9是第四与第五个等腰直角三角形的公共点,…,∵2 021=1 010×2+1,∴A2 021是第1 010个与第1 011个等腰直角三角形的公共点,∴A2 021在x轴正半轴上,∵OA5=4,OA9=6,OA13=8,…,∴OA2 021=(2 021+3)÷2=1 012,∴点A2 021的坐标为(1 012,0),即A2 021的横坐标为1 012.
16.【参考答案】(1)(3,1) (1,2) (7,4) (3分)
(2)(6,1) (6,3) (4,3) (7分)
17.【参考答案】(1)建立平面直角坐标系如图所示,学校和邮局的坐标分别为(1,3),(0,-1).(2分)
(5分)
(2)如图,用线段顺次连接李明家和他在路上经过的地点,得到的图形是帆船. (8分)
18.【参考答案】(1)∵点P在x轴上,
∴2+a=0,解得a=-2,
∴-3a-4=2,
∴点P的坐标为(2,0). (4分)
(2)∵Q(5,8),且PQ∥y轴,
∴-3a-4=5,解得a=-3,
∴2+a=-1,
∴点P的坐标为(5,-1). (8分)
19.【参考答案】(1)如图,点A,C即为所求. (4分)
(2)易知B(-3,4),AC=8,所以S△ABC=×8×4=16. (7分)
(3)点D的坐标为(0,4)或(0,-4). (9分)
20.【参考答案】(1)4 6 (4,6) (3分)
解法提示:∵a,b满足+|b-6|=0,
∴a-4=0,b-6=0,
解得a=4,b=6.
∵四边形OABC为长方形,
∴点B的坐标是(4,6).
(2)当点P移动4秒时,共移动了8个单位长度.
∵OA=4,OC=6,
∴此时点P在线段CB上,离点C的距离是8-6=2(个)单位长度,
∴点P的坐标是(2,6). (6分)
(3)由题意可得,在移动过程中,当点P到x轴的距离为5个单位长度时,存在两种情况:
①当点P在OC上时,
点P移动的时间是5÷2=2.5(秒); (8分)
②当点P在BA上时,
点P移动的时间是(6+4+1)÷2=5.5(秒).
故在移动过程中,当点P到x轴的距离为5个单位长度时,点P移动的时间是2.5秒或5.5秒. (11分)
21.【参考答案】(1)AB==13. (2分)
(2)等腰三角形. (3分)
理由:DE==5,
EF==6,
DF==5,
∴DE=DFEF2,
∴△DEF为等腰三角形. (6分)
(3)如图,作点F关于x轴的对称点F',连接DF'交x轴于点P,则点P即为所求.
∵F(4,2),∴F'(4,-2).
∵D(1,6),
∴DF'==,
∴PD+PF的最短长度为. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师版八年级数学上学期单元测试卷
第三章 位置与坐标
时间:60分钟 满分:100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·广东深圳龙华区期末)家长会前,四个孩子分别向家长描述自己在班里的座位,家长能准确找到自己孩子座位的是 ( )
A.小明说他坐在第1排
B.小白说他坐在第3列
C.小清说她坐在第2排第5列
D.小楚说他的座位靠窗
2.(2021·四川成都郫都区期末)如图,小手盖住的点的坐标可能为 ( )
A.(5,2) B.(-6,3)
C.(-3,-2) D.(3,-3)
3.(2022·广西百色期中)在图中,所画的平面直角坐标系正确的是 ( )
A B
C D
4.(2022·黑龙江哈尔滨道里区期末)在平面直角坐标系中,点A在y轴上,位于原点上方,距离原点2个单位长度,则点A的坐标为 ( )
A.(2,0) B.(-2,0)
C.(0,2) D.(0,-2)
5.(2022·山西晋中期中)如图,在四边形ABCD中,AD∥BC∥x轴,下列说法正确的是 ( )
A.B与C的纵坐标相同
B.C与D的横坐标相同
C.A与D的横坐标相同
D.B与D的纵坐标相同
(第5题) (第6题)
6.如图,雷达探测器测得六个目标A,B,C,D,E,F.按照规定的目标表示方法,目标C,F的位置分别表示为C(6,120°),F(5,210°).按照此方法表示目标A,B,D,E的位置,不正确的是( )
A.A(5,30°) B.B(2,90°)
C.D(4,240°) D.E(3,60°)
7.小莹和小博士下棋,小莹执圆子,小博士执方子,如图,棋盘中心方子的位置用(-1,0)表示,左下角方子的位置用(-2,-1)表示,小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,她放的位置是( )
A.(-2,0) B.(-1,1)
C.(1,-2) D.(-1,-2)
(第7题) (第8题)
8.(2022·山东济宁任城区期末)如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(-5,12),它关于y轴的对称点为B,则△ABO的周长为 ( )
A.24 B.34 C.35 D.36
9.(2021·辽宁锦州期中)下列说法不正确的是( )
A.若x+y=0,则点P(x,y)一定在第二、四象限的角平分线上
B.点P(-2,3)到y轴的距离是2
C.若P(x,y)中xy=0,则点P在x轴上
D.点A(-a2,)可能在第二象限
10.对于平面直角坐标系xOy中的点P(a,b),若点P'的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P'为点P的“k属派生点”,例如:P(1,4)的“2属派生点”为P'(1+2×4,2×1+4),即P'(9,6).若点P在x轴的正半轴上,点P的“k属派生点”为P'点,且线段PP'的长度为线段OP长度的3倍,则k的值为 ( )
A.3 B.±3 C.6 D.±6
二、填空题(共5小题,每小题3分,共15分)
11.如图,已知字母W对应的有序数对为(2,4),有一个英文单词的字母依次对应的有序数对分别为(1,2),(1,3),(2,3),(5,1),请你把这个英文单词写出来 .
12.(2021·重庆北碚区期末)已知点P(a,b)在第三象限,且点P到x轴的距离为4,到y轴的距离为3,则点P的坐标为 .
13.(2022·重庆綦江区期末)在平面直角坐标系中,若点A(m-1,3)与点B(2,n-1)关于x轴对称,则(m+n)2 021的值为 .
14.(2021·江苏南京期末)如图,在平面直角坐标系中,点P为x轴上一点,且到A(0,2)和点B(5,5)的距离相等,则线段OP的长度为 .
(第14题) (第15题)
15.(2022·河南郑州三中期末)如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2 021的横坐标为 .
三、解答题(共6小题,共55分)
16.(7分)如图,我们把杜甫的《绝句》整齐排列放在平面直角坐标系中.
(1)“东”“窗”和“柳”的坐标依次是: , 和 ;
(2)将第2行与第4行对调,再将第4列与第6列对调,(注:最上边一行为第一行,最左边一列为第一列)“里”由开始的坐标 依次变换到 和 .
17.(8分)下图中标明了李明家附近的一些地方,已知李明家位于(-2,-1).
(1)建立平面直角坐标系,写出学校、邮局的坐标.
(2)某星期日早晨,李明从家里出发,沿着(-1,-2),(1,-2),(2,-1),(1,-1),(1,3),(-1,0),(0,-1)的路线转了一下后回到家里,用线段顺次连接李明家和他在路上经过的地点,你能得到什么图形
18.(8分)(2022·浙江宁波期末改编)已知点P(-3a-4,2+a),解答下列问题:
(1)若点P在x轴上,试求出点P的坐标;
(2)若Q(5,8),且PQ∥y轴,试求出点P的坐标.
19.(9分)(2022·河南郑州八中期末)如图,在平面直角坐标内,点A的坐标为(-4,0),点C与点A关于y轴对称.
(1)请在图中标出点A和点C;
(2)求△ABC的面积;
(3)在y轴上有一点D,且S△ACD=S△ABC,写出点D的坐标.
20.(11分)(2021·山东济南期中)如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a,b满足+|b-6|=0,点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着O—C—B—A—O的线路移动一圈停止.
(1)a= ,b= ,点B的坐标为 ;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.
21.(12分)(2022·甘肃白银期末)阅读下列文字,然后回答问题.
已知在平面内有两点P1(x1,y1),P2(x2,y2),它们之间的距离P1P2=.
(1)已知A(2,4),B(-3,-8),试求A,B两点间的距离.
(2)已知△DEF各顶点为D(1,6),E(-2,2),F(4,2),请判断此三角形的形状,并说明理由.
(3)在(2)的条件下,在平面直角坐标系中的x轴上找一点P,使PD+PF的长度最短,求出PD+PF的最短长度.
第三章 位置与坐标
1 2 3 4 5 6 7 8 9 10
C D A C A D B D C B
11.HOPE 12.(-3,4) 13.1
14.4.6 15.1 012
1.C (排除法)小明说他坐在第1排,无法确定座位位置;小白说他坐在第3列,无法确定座位位置;小楚说他的座位靠窗,无法确定座位位置.故选C.
2.D
3.A
4.C ∵在平面直角坐标系中,点A在y轴上,位于原点上方,距离原点2个单位长度,∴A点的坐标是(0,2).
5.A ∵在四边形ABCD中,AD∥BC∥x轴,∴点A与D的纵坐标相同,点B与C的纵坐标相同.
6.D
7.B 棋盘中心方子的位置用(-1,0)表示,则这点所在的横线是x轴,这点向右1个单位所在的纵线是y轴,所以建立平面直角坐标系如图,故小莹将第4枚圆子放的位置是(-1,1)时所有棋子构成轴对称图形.
8.D ∵点A与点B关于y轴对称,A(-5,12),∴B(5,12),∴AB=10,OA=13,OB=13,∴△AOB的周长=OA+OB+AB=13+13+10=36.
9.C ∵x+y=0,∴x=-y,即点在第二、四象限的角平分线上;∵点P的横坐标是-2,∴点P到y轴的距离是2;若P(x,y)中xy=0,则点P可能在x轴上,也可能在y轴上;∵-a2≤0,|b|≥0,∴点A可能在第二象限,也可能在坐标轴上.故选C.
10.B ∵点P在x轴的正半轴上,∴P点的纵坐标为0,设P(a,0),a>0,则点P的“k属派生点”P'点为(a,ka),∴PP'=|ka|,OP=|a|,∵线段PP'的长度为线段OP长度的3倍,∴|ka|=3|a|,∴k=±3.
11.HOPE 由题意知(1,2)表示H,(1,3)表示O,(2,3)表示P,(5,1)表示E,所以这个英文单词为HOPE.
12.(-3,4)
13.1 ∵点A(m-1,3)与点B(2,n-1)关于x轴对称,∴m-1=2,n-1=-3,∴m=3,n=-2,∴(m+n)2 021=(3-2)2 021=1.
14.4.6 设点P(x,0),根据题意得x2+22=(5-x)2+52,解得x=4.6,∴OP=4.6.
15.1 012 ∵A3是第一与第二个等腰直角三角形的公共点,A5是第二与第三个等腰直角三角形的公共点,A7是第三与第四个等腰直角三角形的公共点,A9是第四与第五个等腰直角三角形的公共点,…,∵2 021=1 010×2+1,∴A2 021是第1 010个与第1 011个等腰直角三角形的公共点,∴A2 021在x轴正半轴上,∵OA5=4,OA9=6,OA13=8,…,∴OA2 021=(2 021+3)÷2=1 012,∴点A2 021的坐标为(1 012,0),即A2 021的横坐标为1 012.
16.【参考答案】(1)(3,1) (1,2) (7,4) (3分)
(2)(6,1) (6,3) (4,3) (7分)
17.【参考答案】(1)建立平面直角坐标系如图所示,学校和邮局的坐标分别为(1,3),(0,-1).(2分)
(5分)
(2)如图,用线段顺次连接李明家和他在路上经过的地点,得到的图形是帆船. (8分)
18.【参考答案】(1)∵点P在x轴上,
∴2+a=0,解得a=-2,
∴-3a-4=2,
∴点P的坐标为(2,0). (4分)
(2)∵Q(5,8),且PQ∥y轴,
∴-3a-4=5,解得a=-3,
∴2+a=-1,
∴点P的坐标为(5,-1). (8分)
19.【参考答案】(1)如图,点A,C即为所求. (4分)
(2)易知B(-3,4),AC=8,所以S△ABC=×8×4=16. (7分)
(3)点D的坐标为(0,4)或(0,-4). (9分)
20.【参考答案】(1)4 6 (4,6) (3分)
解法提示:∵a,b满足+|b-6|=0,
∴a-4=0,b-6=0,
解得a=4,b=6.
∵四边形OABC为长方形,
∴点B的坐标是(4,6).
(2)当点P移动4秒时,共移动了8个单位长度.
∵OA=4,OC=6,
∴此时点P在线段CB上,离点C的距离是8-6=2(个)单位长度,
∴点P的坐标是(2,6). (6分)
(3)由题意可得,在移动过程中,当点P到x轴的距离为5个单位长度时,存在两种情况:
①当点P在OC上时,
点P移动的时间是5÷2=2.5(秒); (8分)
②当点P在BA上时,
点P移动的时间是(6+4+1)÷2=5.5(秒).
故在移动过程中,当点P到x轴的距离为5个单位长度时,点P移动的时间是2.5秒或5.5秒. (11分)
21.【参考答案】(1)AB==13. (2分)
(2)等腰三角形. (3分)
理由:DE==5,
EF==6,
DF==5,
∴DE=DF
∴△DEF为等腰三角形. (6分)
(3)如图,作点F关于x轴的对称点F',连接DF'交x轴于点P,则点P即为所求.
∵F(4,2),∴F'(4,-2).
∵D(1,6),
∴DF'==,
∴PD+PF的最短长度为. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
