第一章 勾股定理单元测试卷（含答案）

中小学教育资源及组卷应用平台
2024北师版八年级数学上学期单元测试卷
第一章　勾股定理
时间:60分钟　 满分:100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
　　　　　　 　　　　　　　　　　
1.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且a2-b2=c2,则下列说法正确的是 (　　)
A.∠C是直角 B.∠B是直角
C.∠A是直角 D.∠A是钝角
2.(2021·江西临川二中月考)已知一个直角三角形的三边长的平方和为800,则斜边长为(　　)
A.10 B.20 C.30 D.40
3.(2022·山东枣庄峄城区期中)一个长方形抽屉长3 cm,宽4 cm,贴抽屉底面放一根木棒,那么这根木棒最长(不计木棒粗细)可以是 (　　)
A.4 cm B.5 cm C.6 cm D.7 cm
4.(2022·北京平谷区期末)如图,五根小木棒,其长度分别为5,9,12,13,15,现将它们摆成两个直角三角形,其中正确的是 (　　)
　　　　 　A 　　　　B
　　　　　 C 　　　　D
5.(2022·江苏无锡宜兴期中)如图,有两棵树,一棵高20米,另一棵高10米,两树相距24米.若一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行(　　)
A.26米 B.30米 C.36米 D.40米
6.(2022·江苏南京六合区期中)如图,△ABC中,若AB=20,AC=13,BC=11,AD是BC边上的高,则AD= (　　)
A.5 B.9 C.10 D.12
(第6题)　　　　(第7题)
7.(2022·陕西西安高新一中期中)为了预防新冠疫情,某中学在大门口的正上方A处装着一个红外线激光测温仪,离地AB=2.3米(如图所示),当人体进入感应范围内时,测温仪就会显示人体体温.一个身高1.6米的学生CD正对门,缓慢走到离门2.4米的地方时(BC=2.4米),测温仪自动显示体温,则人头顶离测温仪的距离AD等于 (　　)
A.2.2米 B.2.3米
C.2.4米 D.2.5米
8.(2022·湖南长沙开福区期末)如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,若AB=10 cm,AC=6 cm,则△BED的周长为 (　　)
A.10 cm B.12 cm C.14 cm D.16 cm
(第8题)　　　(第9题)
9.(2022·陕西咸阳期中)在如图所示的网格中,小正方形的边长均为1,△ABC的顶点A,B,C均在正方形顶点上,则下列结论错误的是(　　)
A.S△ABC=10
B.∠BAC=90°
C.AB2=20
D.点A到直线BC的距离是2
10.如图,在△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是 (　　)
A.3.8 B.4.8或3.8
C.4.8 D.5
二、填空题(共5小题,每小题3分,共15分)
11.(2021·山东德州陵城区期末)在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,已知∠C=90°,a∶b=3∶4,c=10,则a=　　　　.
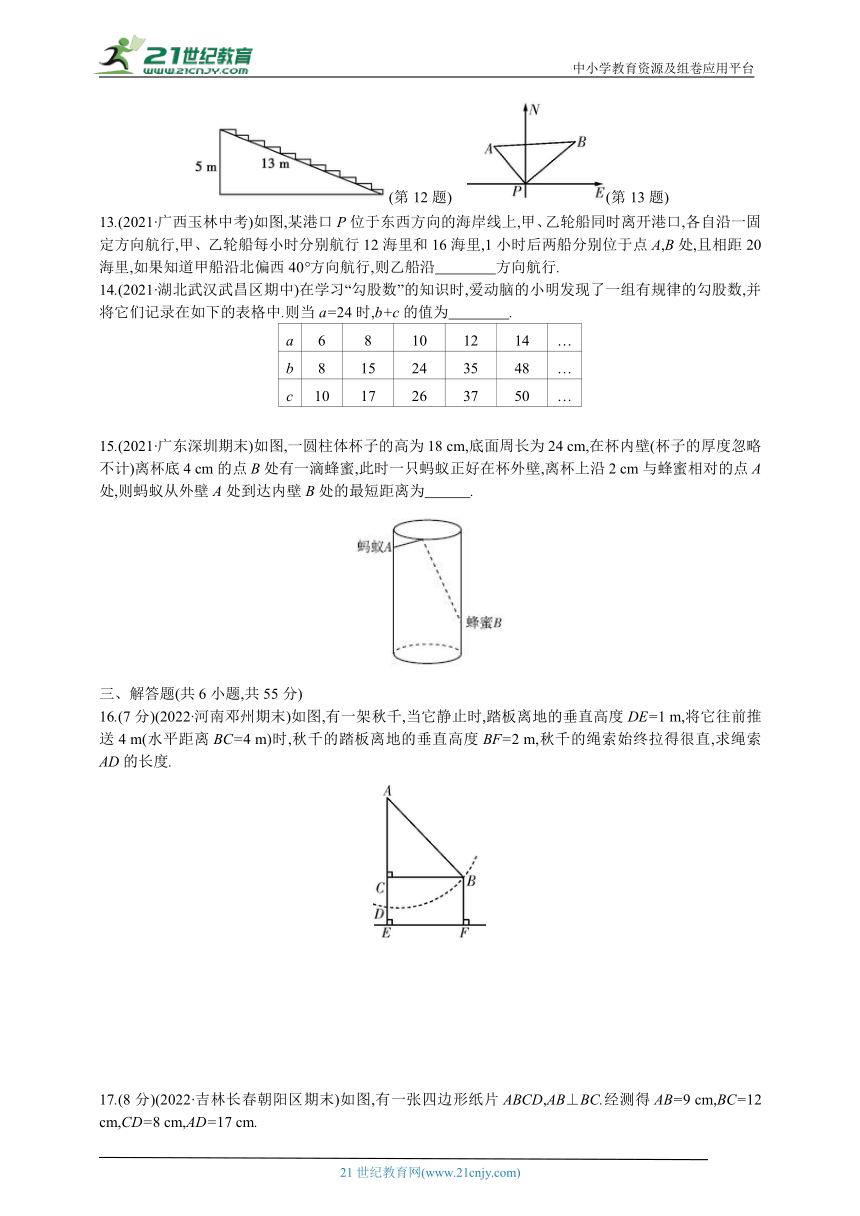
12.如图,在一个高为5 m,长为13 m的楼梯表面铺地毯,地毯的长度至少是　　　　.
(第12题)　(第13题)
13.(2021·广西玉林中考)如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果知道甲船沿北偏西40°方向航行,则乙船沿　　　　方向航行.
14.(2021·湖北武汉武昌区期中)在学习“勾股数”的知识时,爱动脑的小明发现了一组有规律的勾股数,并将它们记录在如下的表格中.则当a=24时,b+c的值为　　　　.
a 6 8 10 12 14 …
b 8 15 24 35 48 …
c 10 17 26 37 50 …
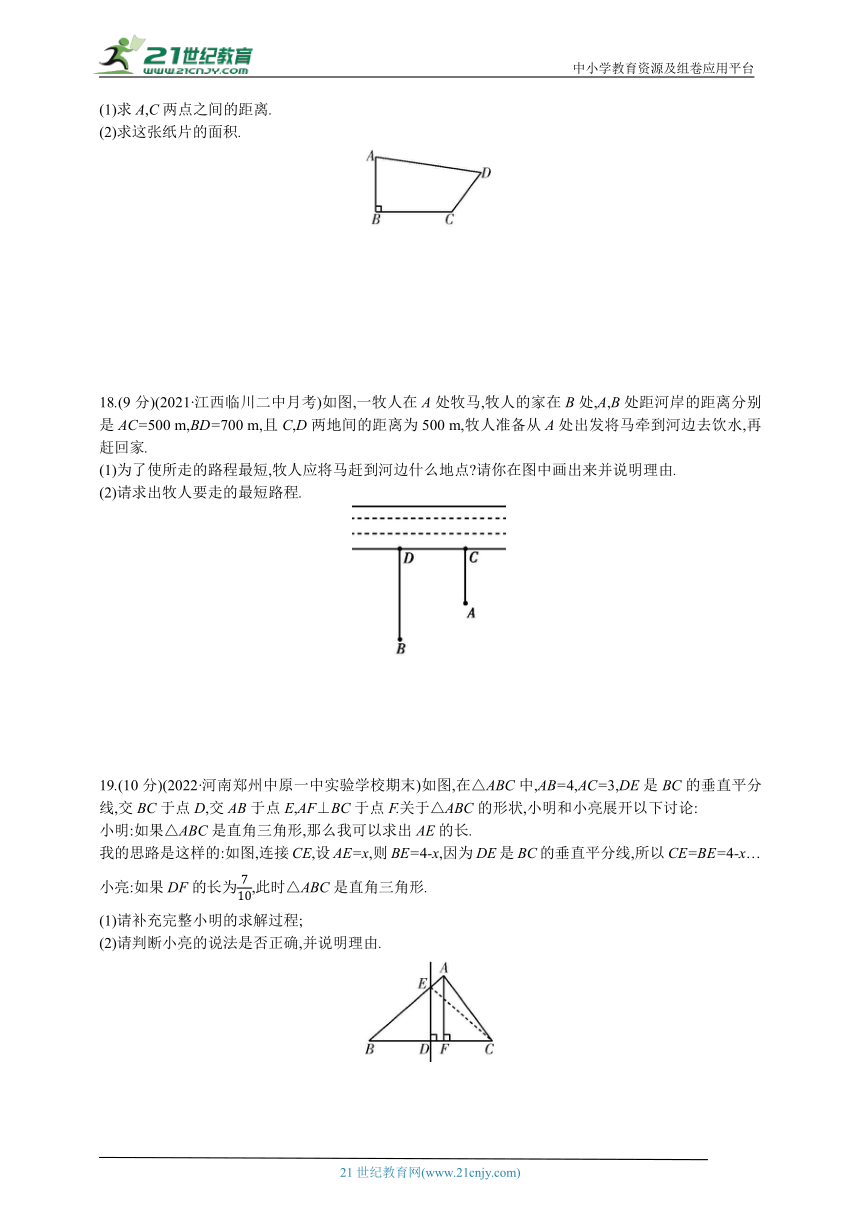
15.(2021·广东深圳期末)如图,一圆柱体杯子的高为18 cm,底面周长为24 cm,在杯内壁(杯子的厚度忽略不计)离杯底4 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为　　　.
三、解答题(共6小题,共55分)
16.(7分)(2022·河南邓州期末)如图,有一架秋千,当它静止时,踏板离地的垂直高度DE=1 m,将它往前推送4 m(水平距离BC=4 m)时,秋千的踏板离地的垂直高度BF=2 m,秋千的绳索始终拉得很直,求绳索AD的长度.
17.(8分)(2022·吉林长春朝阳区期末)如图,有一张四边形纸片ABCD,AB⊥BC.经测得AB=9 cm,BC=12 cm,CD=8 cm,AD=17 cm.
(1)求A,C两点之间的距离.
(2)求这张纸片的面积.
18.(9分)(2021·江西临川二中月考)如图,一牧人在A处牧马,牧人的家在B处,A,B处距河岸的距离分别是AC=500 m,BD=700 m,且C,D两地间的距离为500 m,牧人准备从A处出发将马牵到河边去饮水,再赶回家.
(1)为了使所走的路程最短,牧人应将马赶到河边什么地点 请你在图中画出来并说明理由.
(2)请求出牧人要走的最短路程.
19.(10分)(2022·河南郑州中原一中实验学校期末)如图,在△ABC中,AB=4,AC=3,DE是BC的垂直平分线,交BC于点D,交AB于点E,AF⊥BC于点F.关于△ABC的形状,小明和小亮展开以下讨论:
小明:如果△ABC是直角三角形,那么我可以求出AE的长.
我的思路是这样的:如图,连接CE,设AE=x,则BE=4-x,因为DE是BC的垂直平分线,所以CE=BE=4-x…
小亮:如果DF的长为,此时△ABC是直角三角形.
(1)请补充完整小明的求解过程;
(2)请判断小亮的说法是否正确,并说明理由.
20.(10分)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感,他发现,当两个全等的直角三角形如图(1)或图(2)摆放时,都可以用“面积法”来证明勾股定理.下面是小聪利用图(1)证明勾股定理的过程.
如图(1),△ACB≌△DEA,∠ACB=∠AED=∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,DC,过点D作DF⊥BC交BC的延长线于点F,则DF=EC=b-a,故=S△ACD+S△ABC=b2+ab.
又=S△ADB+S△DCB=c2+a(b-a),
∴b2+ab=c2+a(b-a),
∴a2+b2=c2.
请参照上述证法,利用图(2)进行证明.
将两个全等的直角三角形按图(2)所示摆放,连接BE,其中∠DAB=90°.求证:a2+b2=c2.
　　　　图(1)　　　　　　　　　图(2)
21.(11分)(2022·山东济南槐荫区期中)如图,在Rt△ABC中,∠ACB=90°,AB=5 cm,AC=3 cm,动点P从点B出发沿射线BC以1 cm/s的速度移动,设运动的时间为t s.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
第一章　勾股定理
1 2 3 4 5 6 7 8 9 10
C B B C A D D B A C
11.6 12.17 m 13.北偏东50°
14.288 15.20 cm
1.C　∵a2-b2=c2,∴a2=b2+c2,∴△ABC是直角三角形,且∠A=90°故选C.
2.B　设直角三角形的两条直角边长分别为a,b,斜边长为c.根据勾股定理得a2+b2=c2.∵a2+b2+c2=800,∴2c2=800,∴c2=400,∴c=20.
3.B
4.C　∵52=25,122=144,92=81,152=225,132=169,∴52+122=132,52+92≠122,92+122=152,52+132≠152故选C.
5.A
如图,建立数学模型,两棵树的高度差AC=20-10=10(米),间距AB=DE=24米,根据勾股定理可得,小鸟至少飞行的距离BC==26(米).
6.D　由题意得∠ADB=90°,∴AB2-BD2=AD2=AC2-CD2.∵AB=20,AC=13,BC=11,∴202-(11+CD)2=132-CD2,∴CD=5,∴AD===12.
7.D　如图,过点D作DE⊥AB于点E,∵AB=2.3米,BE=CD=1.6米,ED=BC=2.4米,∴AE=AB-BE=2.3-1.6=0.7(米).在Rt△ADE中,由勾股定理得AD===2.5(米).
8.B　∵AD是∠BAC的平分线,∠C=90°,DE⊥AB于点E,∴CD=DE,∠BAD=∠DAC.在△ACD和△AED中,∴△ACD≌△AED(AAS),∴AC=AE=6 cm,∴BE=AB-AE=10-6=4(cm).由勾股定理得BC===8(cm),∴△BDE的周长=BE+BD+DE=BE+BD+CD=BE+BC=4+8=12(cm).
9.A　S△ABC=4×4-×3×4-×1×2-×2×4=5,A选项中结论错误;∵AC2=12+22=5,AB2=22+42=20,BC2=32+42=25,∴AC2+AB2=BC2,∴∠BAC=90°,B,C选项中结论正确;设点A到直线BC的距离为h,∵BC2=25,∴BC=5,∴×5×h=5,解得h=2,D选项中结论正确.故选A.
10.C　如图,过点A作AF⊥BC于点F,连接AP.在△ABC中,∵AB=AC=5,BC=8,∴BF=4.在Rt△ABF中,由勾股定理易得AF=3.∵S△ABC=S△ABP+S△APC∴×8×3=×5PD+×5PE,即12=×5(PD+PE),则PD+PE=4.8.
11.6　∵在△ABC中,∠C=90°,a∶b=3∶4,∴a∶b∶c=3∶4∶5.∵c=10,∴a=6.
12.17 m　由题意得132-52=122,所以楼梯的水平长度为12 m.因为12+5=17(m),所以地毯的长度至少是17 m.
13.北偏东50°　由题意可知,AP=12,BP=16,AB=20,∵122+162=202,∴△APB是直角三角形,且∠APB=90°,由题意知∠APN=40°,∴∠BPN=90°-∠APN=90°-40°=50°,即乙船沿北偏东50°方向航行
14.288　从题表可知,b=()2-1,c=()2+1,即当a=24时,b=122-1=143,c=122+1=145,b+c=143+145=288.
15.20 cm
将杯子抽象成几何图形(圆柱),并将该圆柱的侧面展开,示意图如图所示.作点A关于EH的对称点A',连接A'B,交EH于点F,则A'B的长即为最短距离.在Rt△A'DB中,由勾股定理得A'B2=A'D2+DB2=122+162=400,∴A'B=20 cm.
16.【参考答案】在Rt△ACB中,BC=4 m,AC2+BC2=AB2.易知CD=CE-DE=BF-DE=1 m,
设AD=x m,则AC=(x-1)m,AB=x m,
故x2=(x-1)2+42,
解得x=8.5.
故绳索AD的长度是8.5 m. (7分)
17.【参考答案】(1)连接AC,如图.
在Rt△ABC中,AB⊥BC,
AB=9 cm,BC=12 cm,
∴AC===15(cm).
故A,C两点之间的距离为15 cm. (4分)
(2)∵CD2+AC2=82+152=172=AD2,
∴∠ACD=90°,
∴四边形纸片ABCD的面积=S△ABC+S△ACD=AB·BC+AC·CD=×9×12+×15×8=54+60=114(cm2).
故这张纸片的面积为114 cm2. (8分)
18.【参考答案】(1)如图(1),点P即为所求. (1分)
理由:作A点关于河岸CD的对称点A',连接BA'交河岸CD于点P,连接PA,则PA=PA'
因为PB+PA=PB+PA'=BA',所以此时路程最短.
所以牧人应将马赶到河边的点P处. (4分)
图(1)　　图(2)
(2)如图(2),过点A'作A'B'⊥BD,交BD的延长线于点B'.
易得DB'=CA'=CA=500 m,B'A'=CD=500 m.
在Rt△BB'A'中,
BB'=BD+DB'=1 200 m,A'B2=B'B2+A'B'2,
所以A'B=1 300 m.
所以牧人要走的最短路程是1 300 m. (9分)
19.【参考答案】(1)补充如下:
因为∠BAC=90°,AC=3,AB=4,
所以AE2+AC2=CE2,
即x2+32=(4-x)2,
解得x=,
即AE=. (4分)
(2)小亮的说法正确. (5分)
理由如下:
设BD=y,则CD=y,
因为DF=,
所以BF=y+,CF=y-.
因为AF⊥BC,
所以AB2-BF2=AF2=AC2-CF2,
即42-(y+)2=32-(y-)2,
解得y=,
所以BC=5.
因为AB2+AC2=42+32=52=BC2,
所以△ABC为直角三角形. (10分)
20.【解题思路】连接BD,过点B作BF⊥DE交DE的延长线于点F,利用“面积法”证明即可.
【参考答案】证明:如图,连接BD,过点B作BF⊥DE交DE的延长线于点F,则BF=b-a. (2分)
∵S四边形ABED=S△ABE+S△ADE=b2+ab,
S四边形ABED=S△ABD+S△BDE=c2+a(b-a),(7分)
∴b2+ab=c2+a(b-a),
∴a2+b2=c2. (10分)
21. 【参考答案】(1)∵∠ACB=90°,
∴在Rt△ABC中,BC2=AB2-AC2=52-32=16,
∴BC=4 cm. (3分)
(2)由题意知BP=t cm.
①如图(1),当∠APB为直角时,点P与点C重合,BP=BC=4 cm,即t=4; (4分)
②如图(2),当∠BAP为直角时,CP=(t-4)cm,
在Rt△ACP中,AP2=32+(t-4)2,
在Rt△BAP中,AB2+AP2=BP2,
即52+[32+(t-4)2]=t2,
解得t=.
　　　　　 图(1)　　　　　　　图(2)
综上所述,当△ABP为直角三角形时,t=4或t=. (7分)
(3)①如图(3),当BP=AB时,t=5;
②如图(4),当AB=AP时,BP=2BC=8 cm,
∴t=8;
③如图(5),当BP=AP时,AP=BP=t cm,CP=(4-t)cm,
在Rt△ACP中,AP2=AC2+CP2,即t2=32+(4-t)2,解得t=.
　　　　 图(3)　　　　 　图(4)　　　　　图(5)
综上所述,当△ABP为等腰三角形时,t=5或t=8或t=. (11分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)