14.2 乘法公式本节综合题(含解析)
文档属性
| 名称 | 14.2 乘法公式本节综合题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 882.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 10:11:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
14.2 乘法公式本节综合题
一、填空题
1.计算: .
2.计算:20182-2017×2019= .
二、单选题
3.已知 , ,则 等于( )
A.8 B.12 C.24 D.25
4.下列运算中,结果正确的是( )
A.2a+3b=5ab B.a2 a3=a6
C.(a+b)2=a2+b2 D.2a﹣(a+b)=a﹣b
5.下列计算正确的是( )
A.2a﹣a=2 B.a2+a=a3
C.(x﹣1)2=x2﹣1 D.(a2)3=a6
6.下列运算正确的是( )
A. B.
C. D.
7.计算: =( )
A. B. C. D.
8.下列运算结果正确的是( )
A. B.
C. D.
9.下列计算正确的是( )
A. B.
C. D.
10.下列运算正确的是( )
A. B.
C. D.(a+b)(a-b)=
11.下列计算正确的是( )
A.(a4)3=a7 B.a8÷a4=a2
C.(ab)3=a3b3 D.(a+b)2=a2+b2
12.下列运算中正确的是( )
A.2a2 a=3a3 B.(ab2)2=ab4
C.2ab2÷b2=2a D.(a+b)2=a2+b2
13.(2+1)(22+1)(24+1)…(216+1)的结果为( )
A.232-1 B.232+1 C.232 D.216
14.下列说法中:①三角形三边高线的交点一定在三角形内部;②八边形有20条对角线;③两个连续偶数的平方差一定是8的倍数;④无论x取何值,代数式的值一定是正数.正确的有( )
A.②④ B.①② C.①③ D.③④
三、解答题
15.试说明不论x,y取何值,代数式x2+y2+6x-4y+15的值总是正数.
16.证明是13的倍数.
四、计算题
17.计算
(1)(2a+1)2-(2a+1)(-1+2a)
(2)(x-y)3(x-y)2(y-x)
(3)(3mn+1)(3mn-1)-8m2n2
18.计算
(1)3ab·(-2ab)+(-3a2b)2
(2)(25m2+15m2n-20m)÷(-5m2)
(3)0.25×(-2)2+16-1-(π-3)0
(4)(a+2b+c)(a+2b-c)
五、综合题
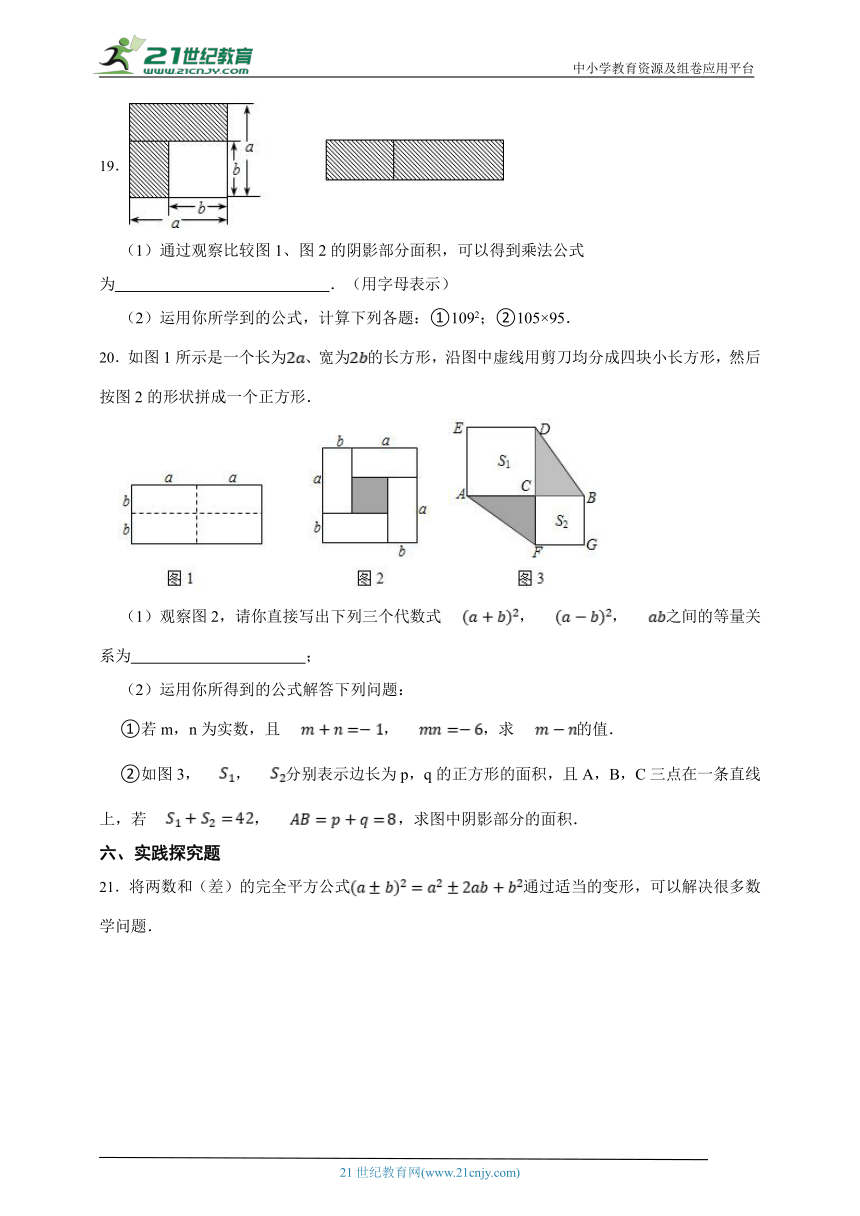
19.
(1)通过观察比较图1、图2的阴影部分面积,可以得到乘法公式为 .(用字母表示)
(2)运用你所学到的公式,计算下列各题:①1092;②105×95.
20.如图1所示是一个长为、宽为的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)观察图2,请你直接写出下列三个代数式,,之间的等量关系为 ;
(2)运用你所得到的公式解答下列问题:
①若m,n为实数,且,,求的值.
②如图3,,分别表示边长为p,q的正方形的面积,且A,B,C三点在一条直线上,若,,求图中阴影部分的面积.
六、实践探究题
21.将两数和(差)的完全平方公式通过适当的变形,可以解决很多数学问题.
例:若,求的值.
解:因为,
所以.
根据上面的解题思路和方法,解决下列问题:
(1)已知,则 ;
(2)若满足,求的值;
(3)如图,在长方形中,,点分别是上的点,且,分别以为边在长方形外侧作正方形和,若长方形的面积为35,求图中阴影部分的面积之和.
答案解析部分
1.【答案】9960
【解析】【解答】解:原式=(99.8+0.2)×(99.8-0.2)
=100×99.6
=9960.
故答案为:9960.
【分析】利用平方差公式计算即可。
2.【答案】1
【解析】【解答】解:原式=20182-(2018-1)×(2018+1)=20182-20182+1=1,
故答案为:1
【分析】将2017×2019进行分解,可转化为平方差公式,再和前面的进行计算求解即可。
3.【答案】B
【解析】【解答】解: , ,
.
.
.
故答案为:B.
【分析】将已知的等式x+2y=6两边同时平方得x2+4y2=24,然后把所求代数式用完全平方公式展开并整体代换计算即可求解.
4.【答案】D
【解析】【解答】解:A、2a+3b不是同类项不能相加减,故本选项错误,
B、a2 a3=a5,故本选项错误,
C、(a+b)2=a2+2ab+b2,故本选项错误,
D、2a﹣(a+b)=a﹣b,故本选项正确,故答案为:D.
【分析】(1)根据合并同类项法则可知,2a与3b不是同类项不能合并;
(2)根据同底数幂的乘法法则:底数不变,指数相加可得,原式=
(3)根据完全平方公式可得原式=+;
(4)根据去括号和合并同类项法则原式=a﹣b.
5.【答案】D
【解析】【解答】解:A、2a﹣a=a,故A错误,不符合题意;
B、a2与a不是同类项,不能合并成一项,故B错误,不符合题意;
C、(x﹣1)2=x2﹣2x+1,故C错误,不符合题意;
D、(a2)3=a6,故D正确,符合题意.
故选:D.
【分析】根据合并同类项的法则判断A、B;根据完全平方公式判断C;根据幂的乘方性质判断D.
6.【答案】D
【解析】【解答】解:A、 ,故本选项错误;
B、 ,故本选项错误;
C、 ,故本选项错误;
D、 ,故本选项正确.
故答案为:D.
【分析】根据合并同类项,幂的乘方,完全平方公式,单项式除法逐项分析即可.
7.【答案】A
【解析】【解答】解:原式=y2﹣y+ ,
故答案为:A.
【分析】将式子利用完全平方公式进行展开即可得到答案。
8.【答案】C
【解析】【解答】,故A不符合题意;
,故B不符合题意;
,故C符合题意;
,故D不符合题意.
故答案为:C.
【分析】根据单项式乘单项式、积的乘方、单项式除以单项式、完全平方公式分别计算,再判断即可.
9.【答案】D
【解析】【解答】解:A.a2和a3不是同类项,无法合并,故本选项错误;
B. ,故本选项错误;
C. ,故本选项错误;
D. ,故本选项正确.
故答案为:D.
【分析】(1)根据同类项的定义“所含字母相同,且相同的字母的指数也相同”可知a2和a3不是同类项,所以不能合并;
(2)由同底数幂相除底数不变指数相减可得原式=a3;
(3)根据完全平方公式可得原式=a2+2ab+b2;
(4)根据积的乘方法则“把积中的每一个因式分别乘方,再把所得的幂相乘”可得原式=4a6.
10.【答案】B
【解析】【解答】解:A、 ,故A选项不符合题意;
B、 ,故B选项符合题意;
C、 ,故C选项不符合题意;
D、(a+b)(a-b)=a2﹣b2,故D选项不符合题意,
故答案为:B.
【分析】所谓同类项,就是所含字母相同,而且相同字母的指数也分别相同的项,合并同类项的时候,只需要将系数相加减,字母和字母的指数都不变,据此判断A;根据同底数幂的乘法,底数不变,指数相加,判断B;根据单项式除以单项式,把系数与相同的字母分别相除,对于只在被除式中含有的字母,则连同指数作为商的一个因式,据此即可判断C;根据两个数的和与两个数的差的积,等于这两个数的平方差,即可判断D.
11.【答案】C
【解析】【解答】∵(a4)3=a12,
∴选项A不符合题意;
∵a8÷a4=a4,
∴选项B不符合题意;
∵(ab)3=a3b3,
∴选项C符合题意;
∵(a+b)2=a2+b2+2ab,
∴选项D不符合题意.
故答案为:C.
【分析】根据同底数幂的除法,完全平方公式的应用,以及幂的乘方与积的乘方的运算方法,逐项判定即可.
12.【答案】C
【解析】【解答】A、2a2 a=2a3 ,故A错误;
B、(ab2)2=a2b4,故B错误;
C、2ab2÷b2=2a,故C正确;
D、(a+b)2=a2+2ab+b2 ,故D错误.
故答案为:D.
【分析】根据单项式乘单项式,积的乘方,单项式除以单项式,完全平方公式分别进行计算,然后判断即可.
13.【答案】A
【解析】【解答】解:原式=(2-1)(2+1)(22+1)(24+1)…(216+1)
=(22-1)(22+1)(24+1)…(216+1)
=(24-1)(24+1)…(216+1)
=(28-1)…(216+1)
=232-1,
故答案为:A.
【分析】将原式变形为(2-1)(2+1)(22+1)(24+1)…(216+1),然后利用平方差公式计算即可.
14.【答案】A
【解析】【解答】① 钝角三角形三边高的交点在三角形外部,故①错误;
② n 边形一共有 条对角线,八边型有条对角线,故②正确;
③ 设两个连续的偶数分别为2n和2n+2,则两个连续的偶数的平方差为:
(2n+2)2-(2 n)2=(4n2+8n+4)-4n2=4n2+8n+4-4n2=8n+4=4(2n+1),不是8的倍数;故③错误;
④ 2x2-2x+1=x2+x2-2x+1=x2+(x2-2x+1)=x2+(x-1)2,因为任何数的平方的结果都是非负数,且x2和(x-1)2不可能同时为零,所以x2+(x-1)2的值一定是正数,故④正确;
故本题应选:A
【分析】①画出锐角、钝角、直角三角形的高观察不同三角形中三角条高的交点位置;② n 边形一共有 条对角线,把边数代入公式计算即可;③设两个连续的偶数分别为2n和2n+2,用式子表示两个连续的偶数的平方差,再化简判断即可;④任何数的平方结果都是非负数;
15.【答案】解答:证明:x2+y2+6x-4y+15 = x2 +6x+9+y2-4y+4+2 =(x+3)2+(y-2)2+2, 因为:(x+3)2≥0, (y-2)2≥0 所以(x+3)2+(y-2)2+2>0, 所以代数式x2+y2+6x-4y+15的值总是正数.
【解析】【分析】先利用完全平方公式将代数式变形,再根据平方的定义得出结论.
16.【答案】证明:,
,
∵26能被13整除,
∴结论成立.
【解析】【分析】利用平方差公式可得924-1=(912+1)(96+1)(93+1)(33+1)(33-1)=26(912+1)(96+1)(93+1)(33+1),据此证明.
17.【答案】解:(1)原式= 4a2+4a+1-(4a2 -1)
=4a2+4a+1-4a2+1
=4a+2
(2) 原式=-(x-y)3(x-y)2(x-y)=-(x-y)6;
(3)原式=9m2n2 -1-8m2n2 =m2n2 -1.
【解析】【分析】
(1)先根据完全平方公式、平方差公式把括号展开,再合并同类项即可求解;
(2)先把底数统一,再按照同底数幂的乘法即可求出结果;
(3)先根据平方差公式把括号展开,合并同类项即可.
18.【答案】(1)解:3a3b (﹣2ab)+(﹣3a2b)2
=﹣6a4b2+9a4b2
=3a4b2
(2)解:(25m2+15m3n﹣20m4)÷(﹣5m2).
=25m2÷(﹣5m2)+15m3n÷(﹣5m2)﹣20m4÷(﹣5m2)
=﹣5﹣3mn+4m2.
(3)解:0.25×(﹣2)﹣2÷16﹣1﹣(π﹣3)0.
=0.25× ÷ ﹣1
= ÷ ﹣1
=1﹣1
=0.
(4)解:(a+2b+c)(a+2b﹣c)
=(a+2b)2﹣c2
=a2+4ab+4b2﹣c2
【解析】【分析】(1)根据单项式乘以单项式法则,合并同类项即可;
(2)根据多项式除以单项式法则进行计算即可;
(3)利用实数运算法则计算即可;
(4)利用平方差公式进行计算即可。
19.【答案】(1)a2﹣b2=(a+b)(a﹣b)
(2)解:①1092
=(100+9)2
=1002+1800+81
=11881,
②105×95
=(100+5)(100﹣5)
=1002﹣52
=9975
【解析】【分析】(1)本题需先根据图中所给的数据,再根据面积公式进行计算,再与两边的图形进行比较,即可求出答案.(2)本题把1092看成(100+9)2,根据完全平方公式解答;105×95=(100+5)×(100﹣5),根据平方差公式的求法进行计算,即可求出答案.
20.【答案】(1)
(2)解:①,,
,
,
或.
②,,分别表示边长为,的正方形的面积,
,,
,
,
,
,
,
,
由图可知,阴影部分面积.
阴影部分面积为11.
【解析】【解答】(1)解:由图可知,
大正方形面积四个矩形的面积中间小正方形的面积,
即,
故答案为:.
【分析】(1)利用不同的表达式表示出阴影部分的面积可得;
(2)①先求出,再求出或即可;
②根据,可得,再结合,求出,最后利用阴影部分的面积求出答案即可。
21.【答案】(1)22
(2)解:设,,则
∵,
∴,
∴即
(3)解:∵,
∴,
∴.
∵长方形的面积为35,
∴,
∴
【解析】【解答】解:(1)∵
∴ 2ab=44,
∴ab=22,
故答案为:22.
【分析】(1)利用完全平方公式进行计算,即可解答;
(2)设2023- x = a,x -2020=b,则a+b = 3,a+b= 2021,然后利用完全平方公式进行计算,即可解答;
(3)根据长方形的性质可得AB =CD = 10,则CF =10-x,CE=6-x,然后设CF=10 -x= a,CE=6-x = b,则a-b = 4,ab = 35,再根据图中阴影部分的面积之和=正方形CFGH的面积+正方形CEMN的面积,以及完全平方公式进行计算,即可解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
14.2 乘法公式本节综合题
一、填空题
1.计算: .
2.计算:20182-2017×2019= .
二、单选题
3.已知 , ,则 等于( )
A.8 B.12 C.24 D.25
4.下列运算中,结果正确的是( )
A.2a+3b=5ab B.a2 a3=a6
C.(a+b)2=a2+b2 D.2a﹣(a+b)=a﹣b
5.下列计算正确的是( )
A.2a﹣a=2 B.a2+a=a3
C.(x﹣1)2=x2﹣1 D.(a2)3=a6
6.下列运算正确的是( )
A. B.
C. D.
7.计算: =( )
A. B. C. D.
8.下列运算结果正确的是( )
A. B.
C. D.
9.下列计算正确的是( )
A. B.
C. D.
10.下列运算正确的是( )
A. B.
C. D.(a+b)(a-b)=
11.下列计算正确的是( )
A.(a4)3=a7 B.a8÷a4=a2
C.(ab)3=a3b3 D.(a+b)2=a2+b2
12.下列运算中正确的是( )
A.2a2 a=3a3 B.(ab2)2=ab4
C.2ab2÷b2=2a D.(a+b)2=a2+b2
13.(2+1)(22+1)(24+1)…(216+1)的结果为( )
A.232-1 B.232+1 C.232 D.216
14.下列说法中:①三角形三边高线的交点一定在三角形内部;②八边形有20条对角线;③两个连续偶数的平方差一定是8的倍数;④无论x取何值,代数式的值一定是正数.正确的有( )
A.②④ B.①② C.①③ D.③④
三、解答题
15.试说明不论x,y取何值,代数式x2+y2+6x-4y+15的值总是正数.
16.证明是13的倍数.
四、计算题
17.计算
(1)(2a+1)2-(2a+1)(-1+2a)
(2)(x-y)3(x-y)2(y-x)
(3)(3mn+1)(3mn-1)-8m2n2
18.计算
(1)3ab·(-2ab)+(-3a2b)2
(2)(25m2+15m2n-20m)÷(-5m2)
(3)0.25×(-2)2+16-1-(π-3)0
(4)(a+2b+c)(a+2b-c)
五、综合题
19.
(1)通过观察比较图1、图2的阴影部分面积,可以得到乘法公式为 .(用字母表示)
(2)运用你所学到的公式,计算下列各题:①1092;②105×95.
20.如图1所示是一个长为、宽为的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)观察图2,请你直接写出下列三个代数式,,之间的等量关系为 ;
(2)运用你所得到的公式解答下列问题:
①若m,n为实数,且,,求的值.
②如图3,,分别表示边长为p,q的正方形的面积,且A,B,C三点在一条直线上,若,,求图中阴影部分的面积.
六、实践探究题
21.将两数和(差)的完全平方公式通过适当的变形,可以解决很多数学问题.
例:若,求的值.
解:因为,
所以.
根据上面的解题思路和方法,解决下列问题:
(1)已知,则 ;
(2)若满足,求的值;
(3)如图,在长方形中,,点分别是上的点,且,分别以为边在长方形外侧作正方形和,若长方形的面积为35,求图中阴影部分的面积之和.
答案解析部分
1.【答案】9960
【解析】【解答】解:原式=(99.8+0.2)×(99.8-0.2)
=100×99.6
=9960.
故答案为:9960.
【分析】利用平方差公式计算即可。
2.【答案】1
【解析】【解答】解:原式=20182-(2018-1)×(2018+1)=20182-20182+1=1,
故答案为:1
【分析】将2017×2019进行分解,可转化为平方差公式,再和前面的进行计算求解即可。
3.【答案】B
【解析】【解答】解: , ,
.
.
.
故答案为:B.
【分析】将已知的等式x+2y=6两边同时平方得x2+4y2=24,然后把所求代数式用完全平方公式展开并整体代换计算即可求解.
4.【答案】D
【解析】【解答】解:A、2a+3b不是同类项不能相加减,故本选项错误,
B、a2 a3=a5,故本选项错误,
C、(a+b)2=a2+2ab+b2,故本选项错误,
D、2a﹣(a+b)=a﹣b,故本选项正确,故答案为:D.
【分析】(1)根据合并同类项法则可知,2a与3b不是同类项不能合并;
(2)根据同底数幂的乘法法则:底数不变,指数相加可得,原式=
(3)根据完全平方公式可得原式=+;
(4)根据去括号和合并同类项法则原式=a﹣b.
5.【答案】D
【解析】【解答】解:A、2a﹣a=a,故A错误,不符合题意;
B、a2与a不是同类项,不能合并成一项,故B错误,不符合题意;
C、(x﹣1)2=x2﹣2x+1,故C错误,不符合题意;
D、(a2)3=a6,故D正确,符合题意.
故选:D.
【分析】根据合并同类项的法则判断A、B;根据完全平方公式判断C;根据幂的乘方性质判断D.
6.【答案】D
【解析】【解答】解:A、 ,故本选项错误;
B、 ,故本选项错误;
C、 ,故本选项错误;
D、 ,故本选项正确.
故答案为:D.
【分析】根据合并同类项,幂的乘方,完全平方公式,单项式除法逐项分析即可.
7.【答案】A
【解析】【解答】解:原式=y2﹣y+ ,
故答案为:A.
【分析】将式子利用完全平方公式进行展开即可得到答案。
8.【答案】C
【解析】【解答】,故A不符合题意;
,故B不符合题意;
,故C符合题意;
,故D不符合题意.
故答案为:C.
【分析】根据单项式乘单项式、积的乘方、单项式除以单项式、完全平方公式分别计算,再判断即可.
9.【答案】D
【解析】【解答】解:A.a2和a3不是同类项,无法合并,故本选项错误;
B. ,故本选项错误;
C. ,故本选项错误;
D. ,故本选项正确.
故答案为:D.
【分析】(1)根据同类项的定义“所含字母相同,且相同的字母的指数也相同”可知a2和a3不是同类项,所以不能合并;
(2)由同底数幂相除底数不变指数相减可得原式=a3;
(3)根据完全平方公式可得原式=a2+2ab+b2;
(4)根据积的乘方法则“把积中的每一个因式分别乘方,再把所得的幂相乘”可得原式=4a6.
10.【答案】B
【解析】【解答】解:A、 ,故A选项不符合题意;
B、 ,故B选项符合题意;
C、 ,故C选项不符合题意;
D、(a+b)(a-b)=a2﹣b2,故D选项不符合题意,
故答案为:B.
【分析】所谓同类项,就是所含字母相同,而且相同字母的指数也分别相同的项,合并同类项的时候,只需要将系数相加减,字母和字母的指数都不变,据此判断A;根据同底数幂的乘法,底数不变,指数相加,判断B;根据单项式除以单项式,把系数与相同的字母分别相除,对于只在被除式中含有的字母,则连同指数作为商的一个因式,据此即可判断C;根据两个数的和与两个数的差的积,等于这两个数的平方差,即可判断D.
11.【答案】C
【解析】【解答】∵(a4)3=a12,
∴选项A不符合题意;
∵a8÷a4=a4,
∴选项B不符合题意;
∵(ab)3=a3b3,
∴选项C符合题意;
∵(a+b)2=a2+b2+2ab,
∴选项D不符合题意.
故答案为:C.
【分析】根据同底数幂的除法,完全平方公式的应用,以及幂的乘方与积的乘方的运算方法,逐项判定即可.
12.【答案】C
【解析】【解答】A、2a2 a=2a3 ,故A错误;
B、(ab2)2=a2b4,故B错误;
C、2ab2÷b2=2a,故C正确;
D、(a+b)2=a2+2ab+b2 ,故D错误.
故答案为:D.
【分析】根据单项式乘单项式,积的乘方,单项式除以单项式,完全平方公式分别进行计算,然后判断即可.
13.【答案】A
【解析】【解答】解:原式=(2-1)(2+1)(22+1)(24+1)…(216+1)
=(22-1)(22+1)(24+1)…(216+1)
=(24-1)(24+1)…(216+1)
=(28-1)…(216+1)
=232-1,
故答案为:A.
【分析】将原式变形为(2-1)(2+1)(22+1)(24+1)…(216+1),然后利用平方差公式计算即可.
14.【答案】A
【解析】【解答】① 钝角三角形三边高的交点在三角形外部,故①错误;
② n 边形一共有 条对角线,八边型有条对角线,故②正确;
③ 设两个连续的偶数分别为2n和2n+2,则两个连续的偶数的平方差为:
(2n+2)2-(2 n)2=(4n2+8n+4)-4n2=4n2+8n+4-4n2=8n+4=4(2n+1),不是8的倍数;故③错误;
④ 2x2-2x+1=x2+x2-2x+1=x2+(x2-2x+1)=x2+(x-1)2,因为任何数的平方的结果都是非负数,且x2和(x-1)2不可能同时为零,所以x2+(x-1)2的值一定是正数,故④正确;
故本题应选:A
【分析】①画出锐角、钝角、直角三角形的高观察不同三角形中三角条高的交点位置;② n 边形一共有 条对角线,把边数代入公式计算即可;③设两个连续的偶数分别为2n和2n+2,用式子表示两个连续的偶数的平方差,再化简判断即可;④任何数的平方结果都是非负数;
15.【答案】解答:证明:x2+y2+6x-4y+15 = x2 +6x+9+y2-4y+4+2 =(x+3)2+(y-2)2+2, 因为:(x+3)2≥0, (y-2)2≥0 所以(x+3)2+(y-2)2+2>0, 所以代数式x2+y2+6x-4y+15的值总是正数.
【解析】【分析】先利用完全平方公式将代数式变形,再根据平方的定义得出结论.
16.【答案】证明:,
,
∵26能被13整除,
∴结论成立.
【解析】【分析】利用平方差公式可得924-1=(912+1)(96+1)(93+1)(33+1)(33-1)=26(912+1)(96+1)(93+1)(33+1),据此证明.
17.【答案】解:(1)原式= 4a2+4a+1-(4a2 -1)
=4a2+4a+1-4a2+1
=4a+2
(2) 原式=-(x-y)3(x-y)2(x-y)=-(x-y)6;
(3)原式=9m2n2 -1-8m2n2 =m2n2 -1.
【解析】【分析】
(1)先根据完全平方公式、平方差公式把括号展开,再合并同类项即可求解;
(2)先把底数统一,再按照同底数幂的乘法即可求出结果;
(3)先根据平方差公式把括号展开,合并同类项即可.
18.【答案】(1)解:3a3b (﹣2ab)+(﹣3a2b)2
=﹣6a4b2+9a4b2
=3a4b2
(2)解:(25m2+15m3n﹣20m4)÷(﹣5m2).
=25m2÷(﹣5m2)+15m3n÷(﹣5m2)﹣20m4÷(﹣5m2)
=﹣5﹣3mn+4m2.
(3)解:0.25×(﹣2)﹣2÷16﹣1﹣(π﹣3)0.
=0.25× ÷ ﹣1
= ÷ ﹣1
=1﹣1
=0.
(4)解:(a+2b+c)(a+2b﹣c)
=(a+2b)2﹣c2
=a2+4ab+4b2﹣c2
【解析】【分析】(1)根据单项式乘以单项式法则,合并同类项即可;
(2)根据多项式除以单项式法则进行计算即可;
(3)利用实数运算法则计算即可;
(4)利用平方差公式进行计算即可。
19.【答案】(1)a2﹣b2=(a+b)(a﹣b)
(2)解:①1092
=(100+9)2
=1002+1800+81
=11881,
②105×95
=(100+5)(100﹣5)
=1002﹣52
=9975
【解析】【分析】(1)本题需先根据图中所给的数据,再根据面积公式进行计算,再与两边的图形进行比较,即可求出答案.(2)本题把1092看成(100+9)2,根据完全平方公式解答;105×95=(100+5)×(100﹣5),根据平方差公式的求法进行计算,即可求出答案.
20.【答案】(1)
(2)解:①,,
,
,
或.
②,,分别表示边长为,的正方形的面积,
,,
,
,
,
,
,
,
由图可知,阴影部分面积.
阴影部分面积为11.
【解析】【解答】(1)解:由图可知,
大正方形面积四个矩形的面积中间小正方形的面积,
即,
故答案为:.
【分析】(1)利用不同的表达式表示出阴影部分的面积可得;
(2)①先求出,再求出或即可;
②根据,可得,再结合,求出,最后利用阴影部分的面积求出答案即可。
21.【答案】(1)22
(2)解:设,,则
∵,
∴,
∴即
(3)解:∵,
∴,
∴.
∵长方形的面积为35,
∴,
∴
【解析】【解答】解:(1)∵
∴ 2ab=44,
∴ab=22,
故答案为:22.
【分析】(1)利用完全平方公式进行计算,即可解答;
(2)设2023- x = a,x -2020=b,则a+b = 3,a+b= 2021,然后利用完全平方公式进行计算,即可解答;
(3)根据长方形的性质可得AB =CD = 10,则CF =10-x,CE=6-x,然后设CF=10 -x= a,CE=6-x = b,则a-b = 4,ab = 35,再根据图中阴影部分的面积之和=正方形CFGH的面积+正方形CEMN的面积,以及完全平方公式进行计算,即可解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
