第12章 一次函数单元测试卷（含答案）

中小学教育资源及组卷应用平台
2024沪科版八年级数学上学期单元测试卷
第12章　一次函数
时间:60分钟　 满分:100分
一、选择题(本大题共10小题,每小题3分,满分30分.每小题有四个选项,其中只有一个选项符合题意)
　　　　　　 　　　　　　　　　　
1.若直线y=kx-5和直线y=-2x+3平行,则k的值为 (　　)
A.2 B.-2 C. D.-
2.(2021·北京期末)已知P1(-3,y1),P2(2,y2)是一次函数y=x+1图象上的两个点,则y1,y2的大小关系是 (　　)
A.y1>y2 B.y1C.y1=y2 D.不能确定
3.若直线y=3x+b经过点(m,n),且n-3m=8,则b的值是 (　　)
A.-4　　　　　　 B.4　　　　　　　　 C.-8　　　　　　 D.8
4.(2021·陕西西安雁塔区期末)已知正比例函数y=kx,每当x增加2时,y就减少3,则k的值为 (　　)
A.- B. C.- D.
5.(2022·山东济南济阳区期末改编)如图,直线l1与l2的交点坐标可以看成下列哪个方程组的解 (　　)
A. B.
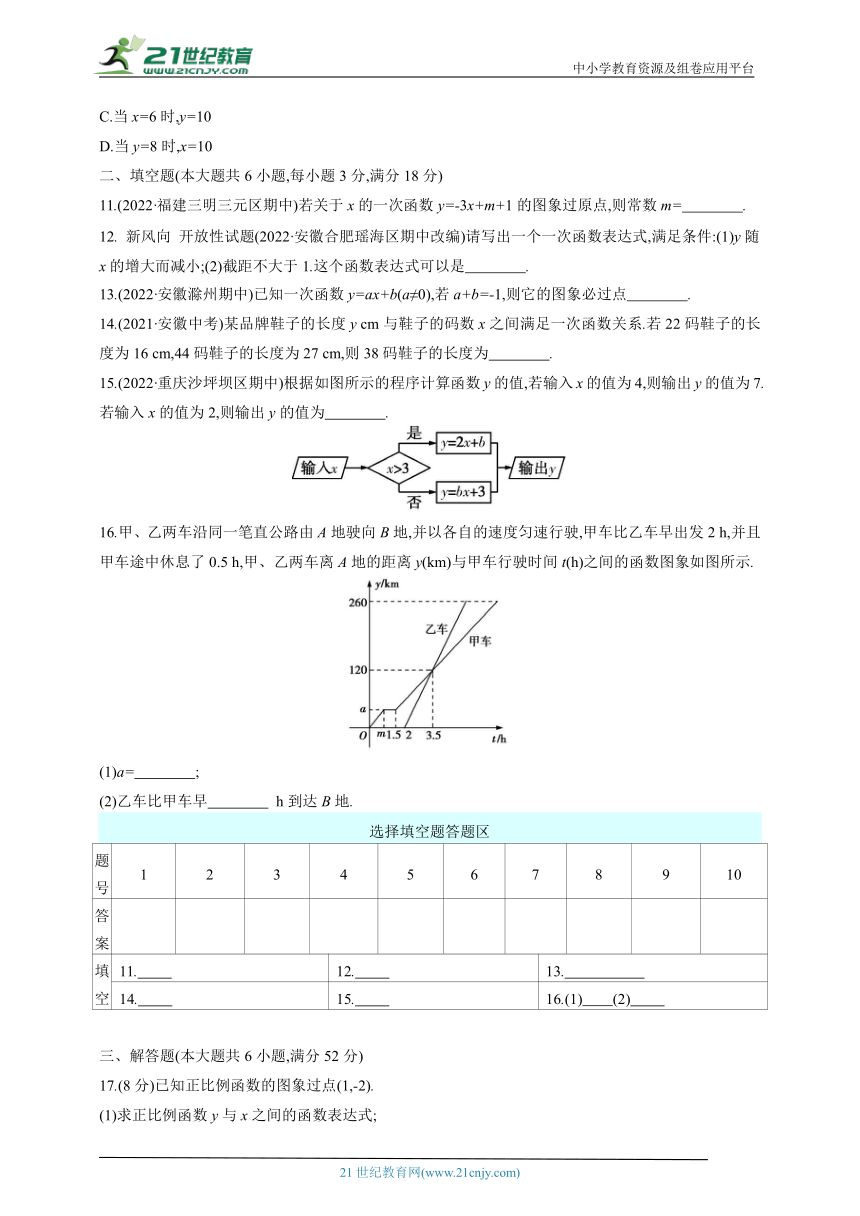
C. D.
6.(2021·陕西西安碑林区期中)已知一次函数y=k1x,y=k2x,y=k3x的图象如图所示,则k1,k2,k3的大小关系为 (　　)
A.k3>k2>k1 B.k1>k3>k2
C.k1>k2>k3 D.k2>k1>k3
7. 新风向 跨学科渗透(2022·福建三明期中改编)已知一弹簧的长度y(cm)与所挂物体的质量m(kg)之间的关系如表(在弹性限度内):
所挂物体的质量m/kg 0 1 2 3 4 5
弹簧的长度y/cm 10 12.5 15 17.5 20 22.5
下列说法错误的是 (　　)
A.在没挂物体时,弹簧的长度为10 cm
B.弹簧的长度随所挂物体的质量的变化而变化,弹簧的长度是自变量,所挂物体的质量是因变量
C.弹簧的长度y(cm)与所挂物体的质量m(kg)之间的关系可用关系式y=2.5m+10来表示
D.在弹簧能承受的范围内,当所挂物体的质量为6 kg时,弹簧的长度为 25 cm
8.若直线y=-2x-4与直线y=4x+b的交点在第三象限,则b的取值范围是 (　　)
A.-48 D.-4≤b≤8
9. 新风向 关注数学文化(2022·湖南岳阳期末改编)元朝朱世杰的《算学启蒙》一书中记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走的路程s关于行走时间t的函数图象,则两图象交点P的坐标是 (　　)
A.(32,4 800) B.(16,2 400) C.(24,3 200) D.(40,5 600)
10.[与动点综合]如图(1),在长方形MNPQ中,动点R从点N出发,沿着N→P→Q→M的方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图(2)所示,那么下列说法不正确的是 (　　)
　　 图(1)　　　　　　　　　　　图(2)
A.当x=2时,y=5
B.长方形MNPQ的周长是18
C.当x=6时,y=10
D.当y=8时,x=10
二、填空题(本大题共6小题,每小题3分,满分18分)
11.(2022·福建三明三元区期中)若关于x的一次函数y=-3x+m+1的图象过原点,则常数m=　　　　.
12. 新风向 开放性试题(2022·安徽合肥瑶海区期中改编)请写出一个一次函数表达式,满足条件:(1)y随x的增大而减小;(2)截距不大于1.这个函数表达式可以是　　　　.
13.(2022·安徽滁州期中)已知一次函数y=ax+b(a≠0),若a+b=-1,则它的图象必过点　　　　.
14.(2021·安徽中考)某品牌鞋子的长度y cm与鞋子的码数x之间满足一次函数关系.若22码鞋子的长度为16 cm,44码鞋子的长度为27 cm,则38码鞋子的长度为　　　　.
15.(2022·重庆沙坪坝区期中)根据如图所示的程序计算函数y的值,若输入x的值为4,则输出y的值为7.若输入x的值为2,则输出y的值为　　　　.
16.甲、乙两车沿同一笔直公路由A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早出发2 h,并且甲车途中休息了0.5 h,甲、乙两车离A地的距离y(km)与甲车行驶时间t(h)之间的函数图象如图所示.
(1)a=　　　　;
(2)乙车比甲车早　　　　 h到达B地.
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11.　　 12.　　 13.　　　　　
14.　　 15.　　 16.(1)　　(2)　　
三、解答题(本大题共6小题,满分52分)
17.(8分)已知正比例函数的图象过点(1,-2).
(1)求正比例函数y与x之间的函数表达式;
(2)若一次函数的图象是由(1)中正比例函数的图象平移得到的,且经过点(1,2),求此一次函数的表达式.
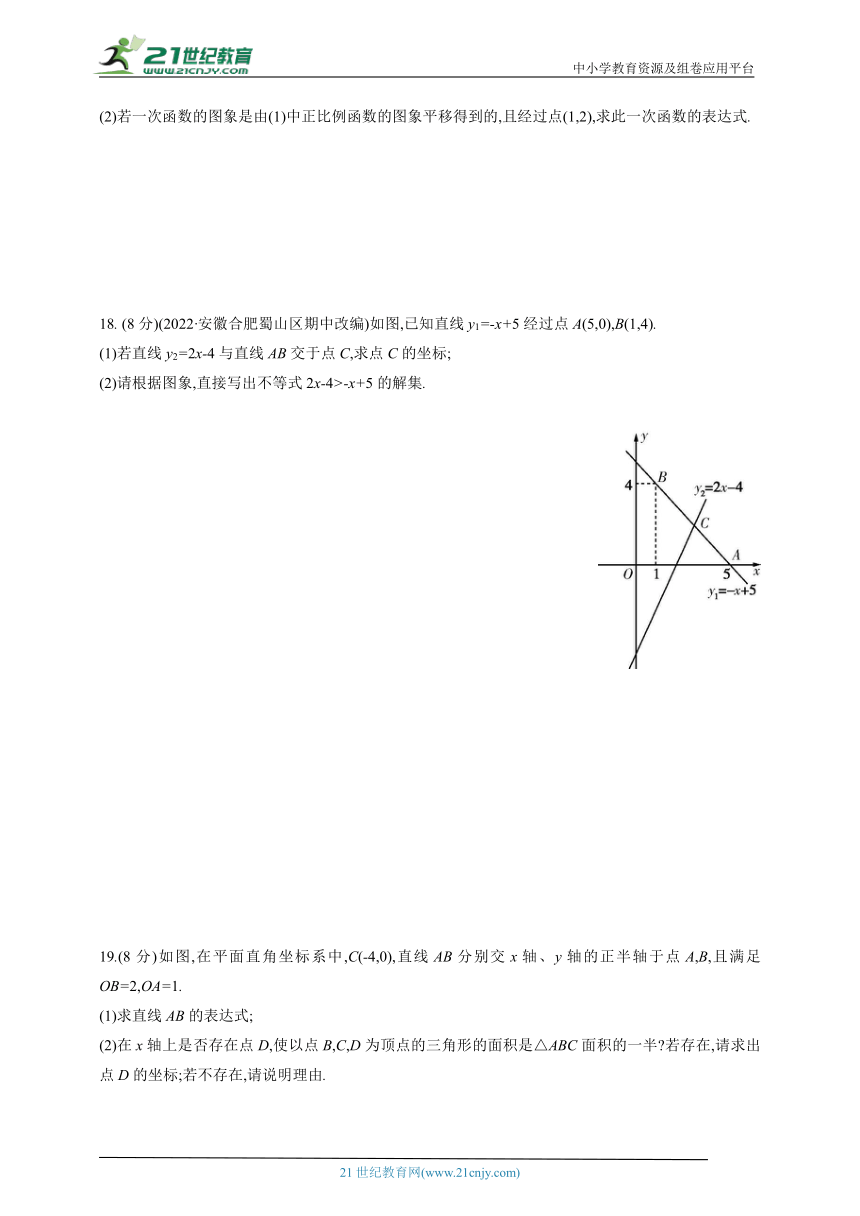
18. (8分)(2022·安徽合肥蜀山区期中改编)如图,已知直线y1=-x+5经过点A(5,0),B(1,4).
(1)若直线y2=2x-4与直线AB交于点C,求点C的坐标;
(2)请根据图象,直接写出不等式2x-4>-x+5的解集.
19.(8分)如图,在平面直角坐标系中,C(-4,0),直线AB分别交x轴、y轴的正半轴于点A,B,且满足OB=2,OA=1.
(1)求直线AB的表达式;
(2)在x轴上是否存在点D,使以点B,C,D为顶点的三角形的面积是△ABC面积的一半 若存在,请求出点D的坐标;若不存在,请说明理由.
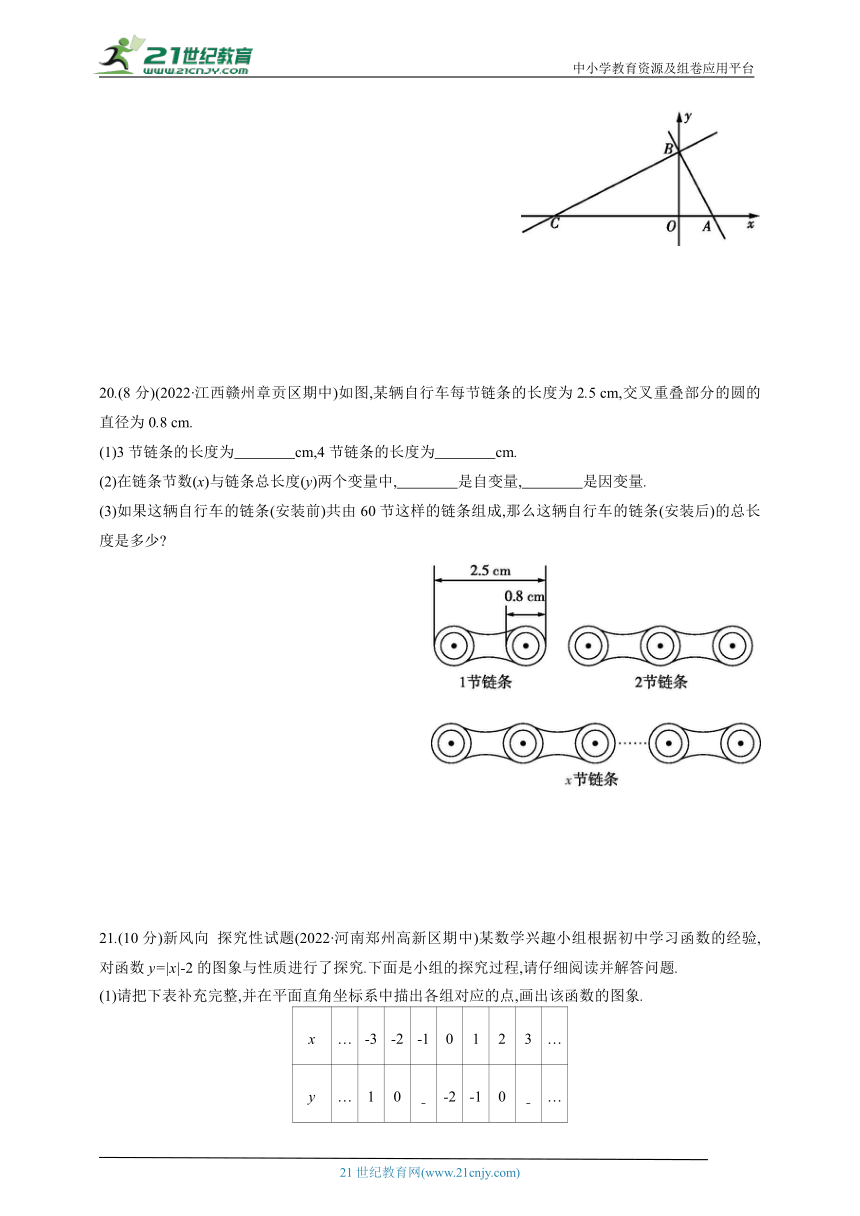
20.(8分)(2022·江西赣州章贡区期中)如图,某辆自行车每节链条的长度为2.5 cm,交叉重叠部分的圆的直径为0.8 cm.
(1)3节链条的长度为　　　　cm,4节链条的长度为　　　　cm.
(2)在链条节数(x)与链条总长度(y)两个变量中,　　　　是自变量,　　　　是因变量.
(3)如果这辆自行车的链条(安装前)共由60节这样的链条组成,那么这辆自行车的链条(安装后)的总长度是多少
21.(10分)新风向 探究性试题(2022·河南郑州高新区期中)某数学兴趣小组根据初中学习函数的经验,对函数y=|x|-2的图象与性质进行了探究.下面是小组的探究过程,请仔细阅读并解答问题.
(1)请把下表补充完整,并在平面直角坐标系中描出各组对应的点,画出该函数的图象.
x … -3 -2 -1 0 1 2 3 …
y … 1 0 -2 -1 0 …
(2)根据函数图象回答下列问题.
①当x=　　　时,y有最小值为　　　.
②请写出该函数的一条性质:　　　　　.
(3)若y=|x|-2的图象与直线y=k有两个交点,则k的取值范围是　　　　.
22.(10分)某经销商从市场得知如下信息:
A品牌手表 B品牌手表
进价/(元/块) 700 100
售价/(元/块) 900 160
该经销商计划一次性购进这两种品牌手表共100块,所用资金不超过4万元,设该经销商购进A品牌手表x块,这两种品牌手表全部销售完后获得的利润为y元.
(1)试写出y与x之间的函数表达式,并求出x的取值范围;
(2)若要求全部销售完后获得的利润不少于 1.26万元,则该经销商有哪几种进货方案
(3)选择哪种进货方案,该经销商可获利最大 最大利润是多少元
第12章　一次函数
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
B B D C A C B A A D
11.-1 12.y=-x+1(答案不唯一) 13.(1,-1)
14.24 15.1 16.(1)40　(2)1.75
1.B　2.B　3.D　4.C　
5.A　由图可知,直线l2过点(2,3),(0,-1),因此直线l2的函数表达式为y=2x-1.直线l1过点(2,3),(0,1),因此直线l1的函数表达式为y=x+1.因此所求的二元一次方程组为
一题多解
(代入验证法)因为直线l1,l2交于点(2,3),所以可将x=2,y=3代入A,B,C,D四个选项进行验证,方程组成立的即为正确选项.
6.C　由题意得,k1为正数,k3k2>k3.
【技巧】|k|越大,图象越陡
7.B　题中表格反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量,弹簧的长度是因变量,故B选项错误.
8.A　将y=-2x-4和y=4x+b联立,得方程组解得因为两直线的交点
在第三象限,所以即解得-49.A　由题意结合函数图象知,良马行走路程s关于行走时间t的函数表达式为y=240(t-12),驽马行走路程s关于行走时间t的函数表达式为y=150t.令150t=240(t-12),解得t=32,则150t=150×32=4 800,所以点P的坐标是(32,4 800).
10.D　由题图可知,MN=5,NP=4.当y=8时,设此时△MNR的高为h,则×5×h=8,则h=,所以点R在PN或QM上.当点R在PN上时,x=;当点R在QM上时,x=,故选D.
11.-1　【提示】将点(0,0)代入一次函数表达式求解
12.y=-x+1【答案不唯一,只要y=kx+b(k<0,b≤1)即可】　
13.(1,-1)　
14.24　由题意易得,y与x之间的函数关系式为y=x+5,所以当x=38时,
y=×38+5=19+5=24,所以38码鞋子的长度为 24 cm.
15.1　当x=4时,y=7,由程序图可得2×4+b=7,解得b=-1,所以当x≤3时,y=-x+3.当x=2时,y=-2+3=1.
16.(1)40　(2)1.75　(1)由题意得,甲车的速度为120÷(3.5-0.5)=40(km/h),
m=1.5-0.5=1,40×1=40(km),所以a=40.(2)因为甲车的行驶速度是40 km/h,所以甲车行驶260 km需要的时间是260÷40=6.5(h).因为甲车中途休息了0.5 h,所以甲车到达B地共用7 h.乙车的速度为120÷(3.5-2)=80(km/h),所以乙车行驶260 km需要的时间是260÷80=3.25(h).7-(2+3.25)=1.75(h),故乙车比甲车早1.75 h到达B地.
17.【参考答案】(1)设正比例函数的表达式为y=ax,将点(1,-2)代入,得a=-2.
所以正比例函数的表达式为y=-2x. (4分)
(2)设一次函数的表达式为y=kx+b. (5分)
依题意有解得
所以一次函数的表达式为y=-2x+4. (8分)
18.【参考答案】(1)因为直线y2=2x-4与直线AB交于点C,所以令y1=y2,
则-x+5=2x-4,解得x=3,所以y=2,所以点C(3,2). (4分)
(2)(数形结合思想)根据图象可得,该解集为 x>3.(8分)
19.【参考答案】(1)因为OB=2,OA=1,
所以点A的坐标为(1,0),点B的坐标为(0,2),
设直线AB的表达式为y=kx+2,
将点A的坐标代入,得0=k+2,解得k=-2,
所以直线AB的表达式为y=-2x+2. (3分)
(2)存在.
设点D的坐标为(x,0),
因为A(1,0),B(0,2),C(-4,0),所以AC=5,
所以S△ABC=×5×2=5.
因为S△BCD=S△ABC,所以S△BCD=CD·OB=,即|x-(-4)|×2=,
所以|x+4|=,所以x=-或x=-,
所以点D的坐标为(-,0)或(-,0). (8分)
20.【参考答案】(1)5.9　7.6 　 (2分)
(2)链条节数(x)　链条总长度(y) (4分)
(3)由(1)可得x节链条的长度为y=2.5x-0.8(x-1)=1.7x+0.8,
所以y与x之间的函数关系式为y=1.7x+0.8.
由题意可得,自行车链条安装后需交叉重叠 0.8 cm,
【易错】自行车链条是环形的,首尾相接会重叠
所以这辆自行车链条(安装后)的总长度为1.7×60+0.8-0.8=102(cm). (8分)
21.【参考答案】(1)补充表格如下. (2分)
x … -3 -2 -1 0 1 2 3 …
y … 1 0 -1 -2 -1 0 1 …
函数图象如图所示. (4分)
(2)①0　-2 (6分)
②函数的图象关于y轴对称(答案不唯一)(8分)
(3)k>-2 (10分)
22.【参考答案】(1)y=(900-700)x+(160-100)·(100-x)=140x+6 000. (2分)
由题意知700x+100(100-x)≤40 000,
解得x≤50,所以0(2)令y≥12 600,即140x+6 000≥12 600,
解得x≥.
又x≤50,所以≤x≤50. (5分)
所以有以下三种进货方案:
①购进A品牌手表48块,B品牌手表52块;
②购进A品牌手表49块,B品牌手表51块;
③购进A品牌手表50块,B品牌手表50块. (6分)
(3)因为y=140x+6 000中,y随x的增大而增大,
所以当x=50时,y取得最大值,最大值为13 000.
所以当购进A品牌手表50块,B品牌手表50块时,该经销商可获利最大,最大利润是13 000元. (10分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)