第14章 全等三角形单元测试卷(含答案)
文档属性
| 名称 | 第14章 全等三角形单元测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024沪科版八年级数学上学期单元测试卷
第14章 全等三角形
时间:60分钟 满分:100分
一、选择题(本大题共10小题,每小题3分,满分30分.每小题有四个选项,其中只有一个选项符合题意)
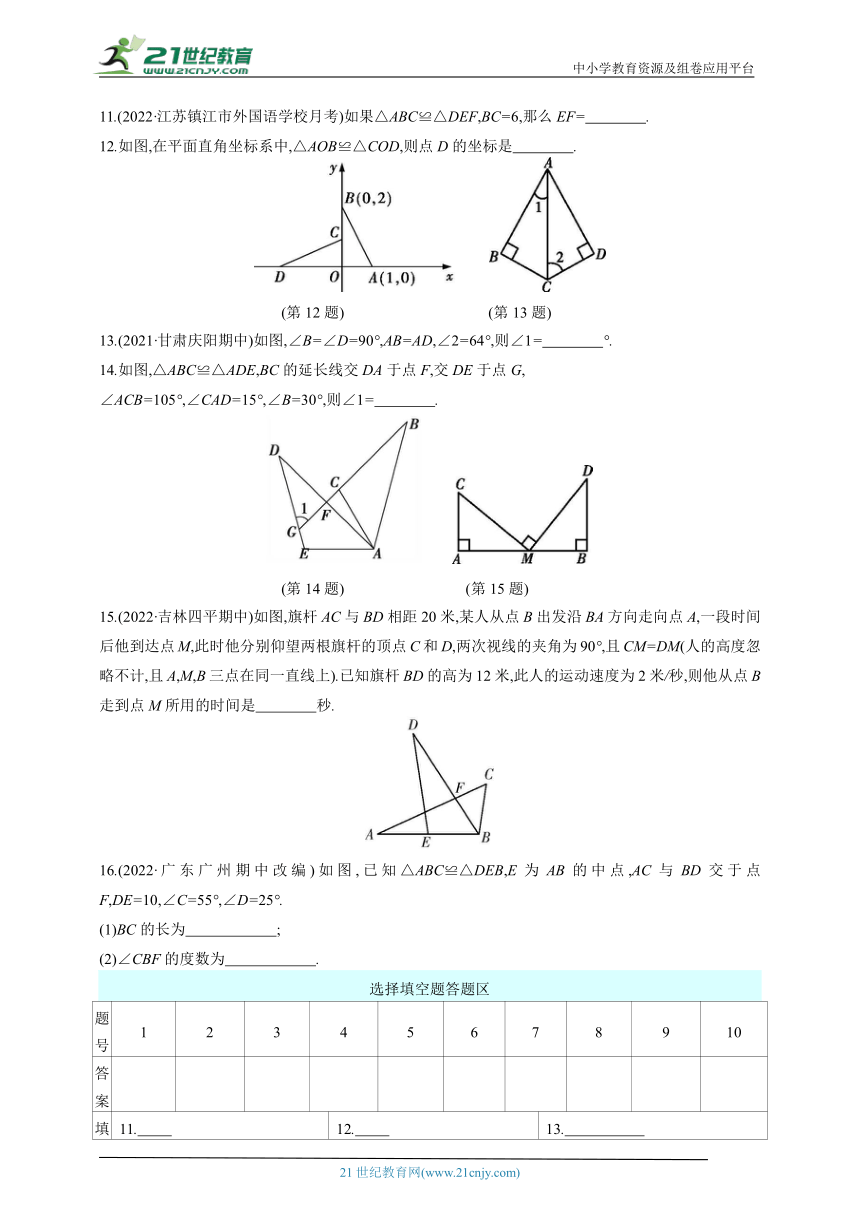
1.(2022·浙江金华期中)判定两个三角形全等有几种方法,下列不能作为判定依据的是 ( )
A.SSS B.SSA C.AAS D.SAS
2.(2022·山东烟台芝罘区期中)如图,已知△ABC≌△DEF,若∠A=80°,∠B=60°,则∠F的度数是 ( )
A.40° B.30° C.70° D.80°
3.(2021·湖北襄阳襄城区期末)如图是由4个相同的小正方形组成的网格图,其中∠1+∠2= ( )
A.150° B.180° C.210° D.225°
(第3题) (第4题)
4.如图是由边长为1的小正方形组成的网格,若△MNP≌△MEQ,则点Q(与点P不重合)可能是图中的 ( )
A.点A B.点B C.点C D.点D
5.(2022·北京丰台区期中)如图,点A,F,C,D在同一条直线上,△ABC≌△DEF,
AF=1,FD=4,则线段FC的长为 ( )
A.1.5 B.2 C.3 D.2.5
(第5题) (第7题)
6.(2022·福建福州鼓楼区期中)下列条件中,不能判定△ABC≌△DEF的是 ( )
A.∠A=∠D,AB=DE,AC=DF
B.∠A=∠D,∠B=∠E,AB=DE
C.∠B=∠E,∠C=∠F,AC=DF
D.∠B=∠E,BC=EF,AC=DF
7.(2022·山东招远期中)如图,△ABC≌△DEC,过点A作AF⊥CD,垂足为点F.若∠BCE=56°,则∠CAF的度数为 ( )
A.34° B.24° C.56° D.36°
8.如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.若∠BEC=70°,则∠EFD= ( )
A.20° B.25° C.35° D.40°
(第8题) (第9题)
9.(2022·广西贵港覃塘区期中)如图,AB=CD,且AB⊥CD,作CE⊥AD,BF⊥AD,垂足分别是E,F,若CE=m,BF=n,EF=k,则线段AD的长是 ( )
A.m+n-k B.m-n+k C.m+k D.n+k
10.(2022·山东烟台期中)如图,已知△ABC的面积为16,BP平分∠ABC,且AP⊥BP,则△BPC的面积是 ( )
A.12 B.6 C.8 D.4
二、填空题(本大题共6小题,每小题3分,满分18分)
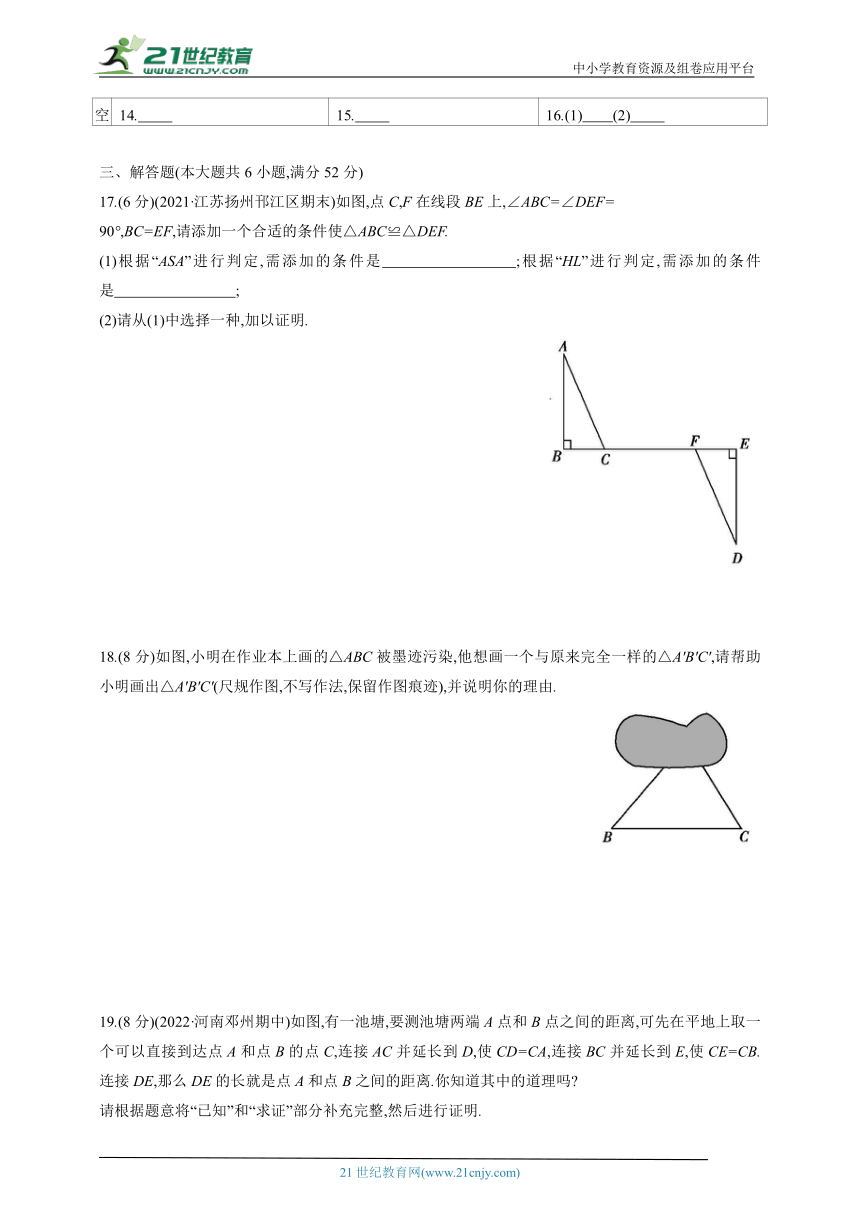
11.(2022·江苏镇江市外国语学校月考)如果△ABC≌△DEF,BC=6,那么EF= .
12.如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是 .
(第12题) (第13题)
13.(2021·甘肃庆阳期中)如图,∠B=∠D=90°,AB=AD,∠2=64°,则∠1= °.
14.如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G,
∠ACB=105°,∠CAD=15°,∠B=30°,则∠1= .
(第14题) (第15题)
15.(2022·吉林四平期中)如图,旗杆AC与BD相距20米,某人从点B出发沿BA方向走向点A,一段时间后他到达点M,此时他分别仰望两根旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM(人的高度忽略不计,且A,M,B三点在同一直线上).已知旗杆BD的高为12米,此人的运动速度为2米/秒,则他从点B走到点M所用的时间是 秒.
16.(2022·广东广州期中改编)如图,已知△ABC≌△DEB,E为AB的中点,AC与BD交于点F,DE=10,∠C=55°,∠D=25°.
(1)BC的长为 ;
(2)∠CBF的度数为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.(1) (2)
三、解答题(本大题共6小题,满分52分)
17.(6分)(2021·江苏扬州邗江区期末)如图,点C,F在线段BE上,∠ABC=∠DEF=
90°,BC=EF,请添加一个合适的条件使△ABC≌△DEF.
(1)根据“ASA”进行判定,需添加的条件是 ;根据“HL”进行判定,需添加的条件是 ;
(2)请从(1)中选择一种,加以证明.
18.(8分)如图,小明在作业本上画的△ABC被墨迹污染,他想画一个与原来完全一样的△A'B'C',请帮助小明画出△A'B'C'(尺规作图,不写作法,保留作图痕迹),并说明你的理由.
19.(8分)(2022·河南邓州期中)如图,有一池塘,要测池塘两端A点和B点之间的距离,可先在平地上取一个可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB.连接DE,那么DE的长就是点A和点B之间的距离.你知道其中的道理吗
请根据题意将“已知”和“求证”部分补充完整,然后进行证明.
(1)已知:AD与BE相交于点C, .
(2)求证: .
(3)证明:
20.(9分)如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
求证:(1)△ABD≌△ACD.
(2)BE=CE.
21.(10分)(2021·安徽合肥期末)如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,点D为AB的中点,如果点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.设运动时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,经过1 s后,△BPD与△CQP是否全等 请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等
22.(11分) 新风向 探究性试题(2022·湖北天门期中)在△ABC中,AB=AC,点D是线段CB上的一动点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图(1),当点D在线段CB上,∠BAC=90°时,∠DCE= °;
(2)设∠BAC=α,∠DCE=β.
①如图(2),当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图(3),当点D在线段CB的延长线上,∠BAC≠90°时,请将图(3)补充完整,并直接写出此时α与β之间的数量关系(不需证明).
图(1) 图(2)
图(3)
第14章 全等三角形
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
B A B D C D A B A C
11.6 12.(-2,0) 13.26
14.60° 15.4 16.(1)5 (2)45°
1.B 2.A 3.B
4.D
图示速解
5.C 6.D
7.A ∵△ABC≌△DEC,∴∠BCA=∠ECD,∴∠BCA-∠ECA=∠ECD-∠ECA,即∠BCE=∠ACF.∵∠BCE=56°,∴∠ACF=56°.∵AF⊥CD,∴∠AFC=90°,
∴∠CAF=90°-∠ACF=90°-56°=34°.
8.B ∵四边形ABCD是正方形,∴BC=CD,∠BCD=∠DCF=90°,∴易得△BCE≌△DCF, ∴∠DFC=∠BEC=70°.∵∠DCF=90°,CE=CF∴∠CFE=∠CEF=45°,∴∠EFD=70°-45°=25°. 故选B.
9.A ∵AB⊥CD,CE⊥AD,∴∠AFB=∠CED=90°,∠A+∠D=90°,∠C+∠D=90°,∴∠A=∠C,∴易证得△ABF≌△CDE(AAS),∴AF=CE=m,DE=BF=n.
∵EF=k,∴DF=ED-EF=n-k,∴AD=AF+DF=m+(n-k)=m+n-k.
C 延长AP交BC于点D.∵BP平分∠ABC,∴∠ABP=∠DBP.又AP⊥BP,
∴∠APB=∠DPB,∴易证得△APB≌△DPB(ASA),
∴AP=PD,∴S△APB=S△DPB,S△APC=S△DPC∴S△BPC=S△ABC=8.
11.6 12.(-2,0)
13.26 由题易证得Rt△ABC≌Rt△ADC(HL),∴∠ACB=∠2=64°,∴∠1=90°-∠ACB=26°.
14.60° ∵△ABC≌△ADE,∴∠D=∠B=30°.∵∠ACB=∠AFC+∠CAF∴∠AFC=∠ACB-∠CAF=105°-15°=90°,∴∠DFG=∠AFC=90°,∴∠1=180°-∠DFG-∠D=60°.
15.4 ∵∠CMD=90°,∴∠CMA+∠DMB=90°.又∠CAM=90°,
∴∠CMA+∠C=90°,∴∠C=∠DMB,∴易证得△ACM≌△BMD(AAS),∴AM=BD=12米,
∴BM=20-12=8(米).∵此人的运动速度为2米/秒,∴他从点B走到点M所用的时间为8÷2=4(秒).
【技巧】时间=路程÷速度
(1)5 (2)45° (1)∵△ABC≌△DEB,DE=10,∴AB=DE=10,BC=BE.∵E为AB的中点,∴BE=AB=5,∴BC=5.(2)∵△ABC≌△DEB,∠C=55°,∠D=25°,∴∠A=∠D=25°,∠DBE=∠C=55°,∴∠ABC=180°-∠A-∠C=180°-25°-55°=100°,∴∠CBF=
∠ABC-∠DBE=100°-55°=45°.
17.【参考答案】(1)∠ACB=∠DFE AC=DF (4分)
(2)选择添加条件AC=DF.
证明:∵∠ABC=∠DEF=90°,
∴在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL). (6分)
一题多解
(2)选择添加条件∠ACB=∠DFE.
证明:在△ABC和△DEF中,
∴△ABC≌△DEF(ASA). (6分)
18.【参考答案】作图如图所示. (4分)
理由:在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(ASA). (8分)
19.【参考答案】(1)CD=CA,CE=CB (2分)
(2)AB=DE (4分)
(3)证明:在△ACB与△DCE中,
∴△ACB≌△DCE(SAS),(6分)
∴AB=DE,
即DE的长就是点A和点B之间的距离. (8分)
20.思路导图
BD=CD△ABD≌△ACD(1)→∠BAE=∠CAE
BE=CE(2)△ABE≌△ACE
【参考答案】证明:(1)∵点D是BC的中点,
∴BD=CD. (1分)
在△ABD和△ACD中,
∴△ABD≌△ACD. (4分)
(2)由(1)知△ABD≌△ACD,
∴∠BAD=∠CAD, 即∠BAE=∠CAE. (5分)
在△ABE和△ACE中, (8分)
∴△ABE≌△ACE,∴BE=CE. (9分)
21.思路导图
(1)速度相同BP=CQ△BPD≌△CQP
(2)△BPD与△CQP全等-
【参考答案】 (1)全等. (1分)
理由:∵t=1,∴BP=CQ=3×1=3(cm). (2分)
∵AB=10 cm,点D为AB的中点,
∴BD=5 cm. (3分)
又PC=BC-BP,BC=8 cm,
∴PC=8-3=5(cm),∴DB=PC. (4分)
又∠B=∠C,∴△BPD≌△CQP. (5分)
(2)设点Q的运动速度为x cm/s,则BD=5 cm,BP=3t cm,CP=(8-3t)cm,CQ=xt cm.
∵点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ.
若使△BPD与△CPQ全等, (7分)
只能是BP=CP,BD=CQ,∴3t=8-3t,xt=5,
∴点P,点Q的运动时间 t= s, (9分)
∴点Q的运动速度为5÷= (cm/s).
即当点Q的运动速度为 cm/s时,能够使△BPD与△CQP全等. (10分)
22.【参考答案】(“手拉手”模型)(1)90 (2分)
(2)①α+β=180°.
证明:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE. (3分)
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),∴∠B=∠ACE. (5分)
∵∠B+∠ACB=180°-α,
∴∠DCE=∠ACE+∠ACB=∠B+∠ACB=180°-α=β,∴α+β=180°. (7分)
②如图所示. (9分)
α=β. (11分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024沪科版八年级数学上学期单元测试卷
第14章 全等三角形
时间:60分钟 满分:100分
一、选择题(本大题共10小题,每小题3分,满分30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·浙江金华期中)判定两个三角形全等有几种方法,下列不能作为判定依据的是 ( )
A.SSS B.SSA C.AAS D.SAS
2.(2022·山东烟台芝罘区期中)如图,已知△ABC≌△DEF,若∠A=80°,∠B=60°,则∠F的度数是 ( )
A.40° B.30° C.70° D.80°
3.(2021·湖北襄阳襄城区期末)如图是由4个相同的小正方形组成的网格图,其中∠1+∠2= ( )
A.150° B.180° C.210° D.225°
(第3题) (第4题)
4.如图是由边长为1的小正方形组成的网格,若△MNP≌△MEQ,则点Q(与点P不重合)可能是图中的 ( )
A.点A B.点B C.点C D.点D
5.(2022·北京丰台区期中)如图,点A,F,C,D在同一条直线上,△ABC≌△DEF,
AF=1,FD=4,则线段FC的长为 ( )
A.1.5 B.2 C.3 D.2.5
(第5题) (第7题)
6.(2022·福建福州鼓楼区期中)下列条件中,不能判定△ABC≌△DEF的是 ( )
A.∠A=∠D,AB=DE,AC=DF
B.∠A=∠D,∠B=∠E,AB=DE
C.∠B=∠E,∠C=∠F,AC=DF
D.∠B=∠E,BC=EF,AC=DF
7.(2022·山东招远期中)如图,△ABC≌△DEC,过点A作AF⊥CD,垂足为点F.若∠BCE=56°,则∠CAF的度数为 ( )
A.34° B.24° C.56° D.36°
8.如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.若∠BEC=70°,则∠EFD= ( )
A.20° B.25° C.35° D.40°
(第8题) (第9题)
9.(2022·广西贵港覃塘区期中)如图,AB=CD,且AB⊥CD,作CE⊥AD,BF⊥AD,垂足分别是E,F,若CE=m,BF=n,EF=k,则线段AD的长是 ( )
A.m+n-k B.m-n+k C.m+k D.n+k
10.(2022·山东烟台期中)如图,已知△ABC的面积为16,BP平分∠ABC,且AP⊥BP,则△BPC的面积是 ( )
A.12 B.6 C.8 D.4
二、填空题(本大题共6小题,每小题3分,满分18分)
11.(2022·江苏镇江市外国语学校月考)如果△ABC≌△DEF,BC=6,那么EF= .
12.如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是 .
(第12题) (第13题)
13.(2021·甘肃庆阳期中)如图,∠B=∠D=90°,AB=AD,∠2=64°,则∠1= °.
14.如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G,
∠ACB=105°,∠CAD=15°,∠B=30°,则∠1= .
(第14题) (第15题)
15.(2022·吉林四平期中)如图,旗杆AC与BD相距20米,某人从点B出发沿BA方向走向点A,一段时间后他到达点M,此时他分别仰望两根旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM(人的高度忽略不计,且A,M,B三点在同一直线上).已知旗杆BD的高为12米,此人的运动速度为2米/秒,则他从点B走到点M所用的时间是 秒.
16.(2022·广东广州期中改编)如图,已知△ABC≌△DEB,E为AB的中点,AC与BD交于点F,DE=10,∠C=55°,∠D=25°.
(1)BC的长为 ;
(2)∠CBF的度数为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.(1) (2)
三、解答题(本大题共6小题,满分52分)
17.(6分)(2021·江苏扬州邗江区期末)如图,点C,F在线段BE上,∠ABC=∠DEF=
90°,BC=EF,请添加一个合适的条件使△ABC≌△DEF.
(1)根据“ASA”进行判定,需添加的条件是 ;根据“HL”进行判定,需添加的条件是 ;
(2)请从(1)中选择一种,加以证明.
18.(8分)如图,小明在作业本上画的△ABC被墨迹污染,他想画一个与原来完全一样的△A'B'C',请帮助小明画出△A'B'C'(尺规作图,不写作法,保留作图痕迹),并说明你的理由.
19.(8分)(2022·河南邓州期中)如图,有一池塘,要测池塘两端A点和B点之间的距离,可先在平地上取一个可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB.连接DE,那么DE的长就是点A和点B之间的距离.你知道其中的道理吗
请根据题意将“已知”和“求证”部分补充完整,然后进行证明.
(1)已知:AD与BE相交于点C, .
(2)求证: .
(3)证明:
20.(9分)如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
求证:(1)△ABD≌△ACD.
(2)BE=CE.
21.(10分)(2021·安徽合肥期末)如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,点D为AB的中点,如果点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.设运动时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,经过1 s后,△BPD与△CQP是否全等 请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等
22.(11分) 新风向 探究性试题(2022·湖北天门期中)在△ABC中,AB=AC,点D是线段CB上的一动点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图(1),当点D在线段CB上,∠BAC=90°时,∠DCE= °;
(2)设∠BAC=α,∠DCE=β.
①如图(2),当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论;
②如图(3),当点D在线段CB的延长线上,∠BAC≠90°时,请将图(3)补充完整,并直接写出此时α与β之间的数量关系(不需证明).
图(1) 图(2)
图(3)
第14章 全等三角形
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
B A B D C D A B A C
11.6 12.(-2,0) 13.26
14.60° 15.4 16.(1)5 (2)45°
1.B 2.A 3.B
4.D
图示速解
5.C 6.D
7.A ∵△ABC≌△DEC,∴∠BCA=∠ECD,∴∠BCA-∠ECA=∠ECD-∠ECA,即∠BCE=∠ACF.∵∠BCE=56°,∴∠ACF=56°.∵AF⊥CD,∴∠AFC=90°,
∴∠CAF=90°-∠ACF=90°-56°=34°.
8.B ∵四边形ABCD是正方形,∴BC=CD,∠BCD=∠DCF=90°,∴易得△BCE≌△DCF, ∴∠DFC=∠BEC=70°.∵∠DCF=90°,CE=CF∴∠CFE=∠CEF=45°,∴∠EFD=70°-45°=25°. 故选B.
9.A ∵AB⊥CD,CE⊥AD,∴∠AFB=∠CED=90°,∠A+∠D=90°,∠C+∠D=90°,∴∠A=∠C,∴易证得△ABF≌△CDE(AAS),∴AF=CE=m,DE=BF=n.
∵EF=k,∴DF=ED-EF=n-k,∴AD=AF+DF=m+(n-k)=m+n-k.
C 延长AP交BC于点D.∵BP平分∠ABC,∴∠ABP=∠DBP.又AP⊥BP,
∴∠APB=∠DPB,∴易证得△APB≌△DPB(ASA),
∴AP=PD,∴S△APB=S△DPB,S△APC=S△DPC∴S△BPC=S△ABC=8.
11.6 12.(-2,0)
13.26 由题易证得Rt△ABC≌Rt△ADC(HL),∴∠ACB=∠2=64°,∴∠1=90°-∠ACB=26°.
14.60° ∵△ABC≌△ADE,∴∠D=∠B=30°.∵∠ACB=∠AFC+∠CAF∴∠AFC=∠ACB-∠CAF=105°-15°=90°,∴∠DFG=∠AFC=90°,∴∠1=180°-∠DFG-∠D=60°.
15.4 ∵∠CMD=90°,∴∠CMA+∠DMB=90°.又∠CAM=90°,
∴∠CMA+∠C=90°,∴∠C=∠DMB,∴易证得△ACM≌△BMD(AAS),∴AM=BD=12米,
∴BM=20-12=8(米).∵此人的运动速度为2米/秒,∴他从点B走到点M所用的时间为8÷2=4(秒).
【技巧】时间=路程÷速度
(1)5 (2)45° (1)∵△ABC≌△DEB,DE=10,∴AB=DE=10,BC=BE.∵E为AB的中点,∴BE=AB=5,∴BC=5.(2)∵△ABC≌△DEB,∠C=55°,∠D=25°,∴∠A=∠D=25°,∠DBE=∠C=55°,∴∠ABC=180°-∠A-∠C=180°-25°-55°=100°,∴∠CBF=
∠ABC-∠DBE=100°-55°=45°.
17.【参考答案】(1)∠ACB=∠DFE AC=DF (4分)
(2)选择添加条件AC=DF.
证明:∵∠ABC=∠DEF=90°,
∴在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL). (6分)
一题多解
(2)选择添加条件∠ACB=∠DFE.
证明:在△ABC和△DEF中,
∴△ABC≌△DEF(ASA). (6分)
18.【参考答案】作图如图所示. (4分)
理由:在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(ASA). (8分)
19.【参考答案】(1)CD=CA,CE=CB (2分)
(2)AB=DE (4分)
(3)证明:在△ACB与△DCE中,
∴△ACB≌△DCE(SAS),(6分)
∴AB=DE,
即DE的长就是点A和点B之间的距离. (8分)
20.思路导图
BD=CD△ABD≌△ACD(1)→∠BAE=∠CAE
BE=CE(2)△ABE≌△ACE
【参考答案】证明:(1)∵点D是BC的中点,
∴BD=CD. (1分)
在△ABD和△ACD中,
∴△ABD≌△ACD. (4分)
(2)由(1)知△ABD≌△ACD,
∴∠BAD=∠CAD, 即∠BAE=∠CAE. (5分)
在△ABE和△ACE中, (8分)
∴△ABE≌△ACE,∴BE=CE. (9分)
21.思路导图
(1)速度相同BP=CQ△BPD≌△CQP
(2)△BPD与△CQP全等-
【参考答案】 (1)全等. (1分)
理由:∵t=1,∴BP=CQ=3×1=3(cm). (2分)
∵AB=10 cm,点D为AB的中点,
∴BD=5 cm. (3分)
又PC=BC-BP,BC=8 cm,
∴PC=8-3=5(cm),∴DB=PC. (4分)
又∠B=∠C,∴△BPD≌△CQP. (5分)
(2)设点Q的运动速度为x cm/s,则BD=5 cm,BP=3t cm,CP=(8-3t)cm,CQ=xt cm.
∵点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ.
若使△BPD与△CPQ全等, (7分)
只能是BP=CP,BD=CQ,∴3t=8-3t,xt=5,
∴点P,点Q的运动时间 t= s, (9分)
∴点Q的运动速度为5÷= (cm/s).
即当点Q的运动速度为 cm/s时,能够使△BPD与△CQP全等. (10分)
22.【参考答案】(“手拉手”模型)(1)90 (2分)
(2)①α+β=180°.
证明:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE. (3分)
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),∴∠B=∠ACE. (5分)
∵∠B+∠ACB=180°-α,
∴∠DCE=∠ACE+∠ACB=∠B+∠ACB=180°-α=β,∴α+β=180°. (7分)
②如图所示. (9分)
α=β. (11分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
