沪科版2023-2024学年度上学期八年级期中测试数学卷(含答案)
文档属性
| 名称 | 沪科版2023-2024学年度上学期八年级期中测试数学卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 13:14:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024沪科版八年级数学上学期单元测试卷
八年级上学期期中综合测评卷
时间:120分钟 满分:150分
一、选择题(本大题共10小题,每小题4分,满分40分.每小题有四个选项,其中只有一个选项符合题意)
1.若y=mx|m-1|是正比例函数,则m的值是 ( )
A.0 B.1 C.2 D.0或-2
2.三角形的一个外角小于与它相邻的内角,这个三角形是 ( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不确定
3.已知点A(m,n)在第三象限,则点B(|m|,-n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.下列选项中,可以用来证明命题“若a2>4,则a>2”是假命题的反例是 ( )
A.a=-3 B.a=-2 C.a=2 D.a=3
5.已知三角形三边长分别为a,b,c,其中a,b满足|a-3|+(b-7)2=0,那么这个三角形的最大边长c的值可以是 ( )
A.10 B.8 C.5 D.6
6.已知点A(1,-3),点B(2,-1),将线段AB平移至A1B1.若点A1(a,1),点B1(3,-b),则a-b的值为 ( )
A.1 B.-1 C.5 D.-5
7.已知正比例函数y=kx(k≠0)的图象过点(-2,-3),把正比例函数的图象平移,使它过点(1,-1),则平移后的函数图象大致是 ( )
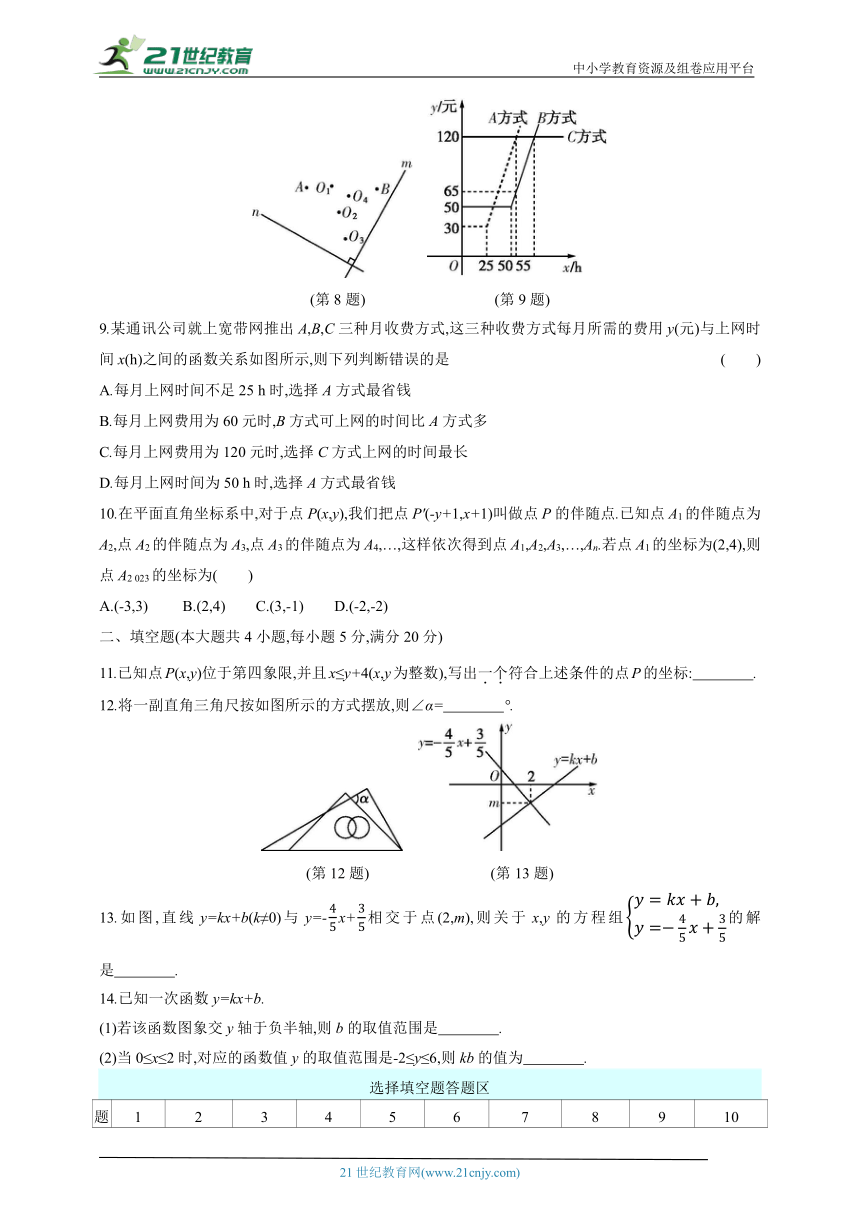
8.如图,直线m⊥n,在平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(-1,2),点B的坐标为(2,-4),则坐标原点为 ( )
A.O1 B.O2 C.O3 D.O4
(第8题) (第9题)
9.某通讯公司就上宽带网推出A,B,C三种月收费方式,这三种收费方式每月所需的费用y(元)与上网时间x(h)之间的函数关系如图所示,则下列判断错误的是 ( )
A.每月上网时间不足25 h时,选择A方式最省钱
B.每月上网费用为60元时,B方式可上网的时间比A方式多
C.每月上网费用为120元时,选择C方式上网的时间最长
D.每月上网时间为50 h时,选择A方式最省钱
10.在平面直角坐标系中,对于点P(x,y),我们把点P'(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.若点A1的坐标为(2,4),则点A2 023的坐标为( )
A.(-3,3) B.(2,4) C.(3,-1) D.(-2,-2)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),写出一个符合上述条件的点P的坐标: .
12.将一副直角三角尺按如图所示的方式摆放,则∠α= °.
(第12题) (第13题)
13.如图,直线y=kx+b(k≠0)与y=-x+相交于点(2,m),则关于x,y的方程组的解是 .
14.已知一次函数y=kx+b.
(1)若该函数图象交y轴于负半轴,则b的取值范围是 .
(2)当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤6,则kb的值为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14.(1) (2)
三、(本大题共2小题,每小题8分,满分16分)
15.已知一次函数y=(3-k)x-2k+18.
(1)当k为何值时,这个一次函数的图象经过原点
(2)当k为何值时,y随x的增大而减小
16.已知点P(2a+3,a-1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3.
(2)点P在过点A(2,-3)且与x轴平行的直线上.
四、(本大题共2小题,每小题8分,满分16分)
17.如图所示,AE为△ABC的角平分线,CD为△ABC的高.若∠B=30°,∠ACB=70°.
(1)求∠CAF的度数.
(2)求∠AFC的度数.
18.象棋在中国有近三千年的历史,中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“馬”走的规则是沿“日”形的对角线走.例如:图中“馬”由所在的位置可以直接走到点A,B处.
(1)若“帥”位于点(0,0),“相”位于点(4,2),则“馬”所在的点的坐标为 ,点C的坐标为 ,点D的坐标为 .
(2)若“馬”的位置在C点,为了到达D点,请按“馬”走的规则,写出一种你认为合理的行走路线(用坐标表示).
五、(本大题共2小题,每小题10分,满分20分)
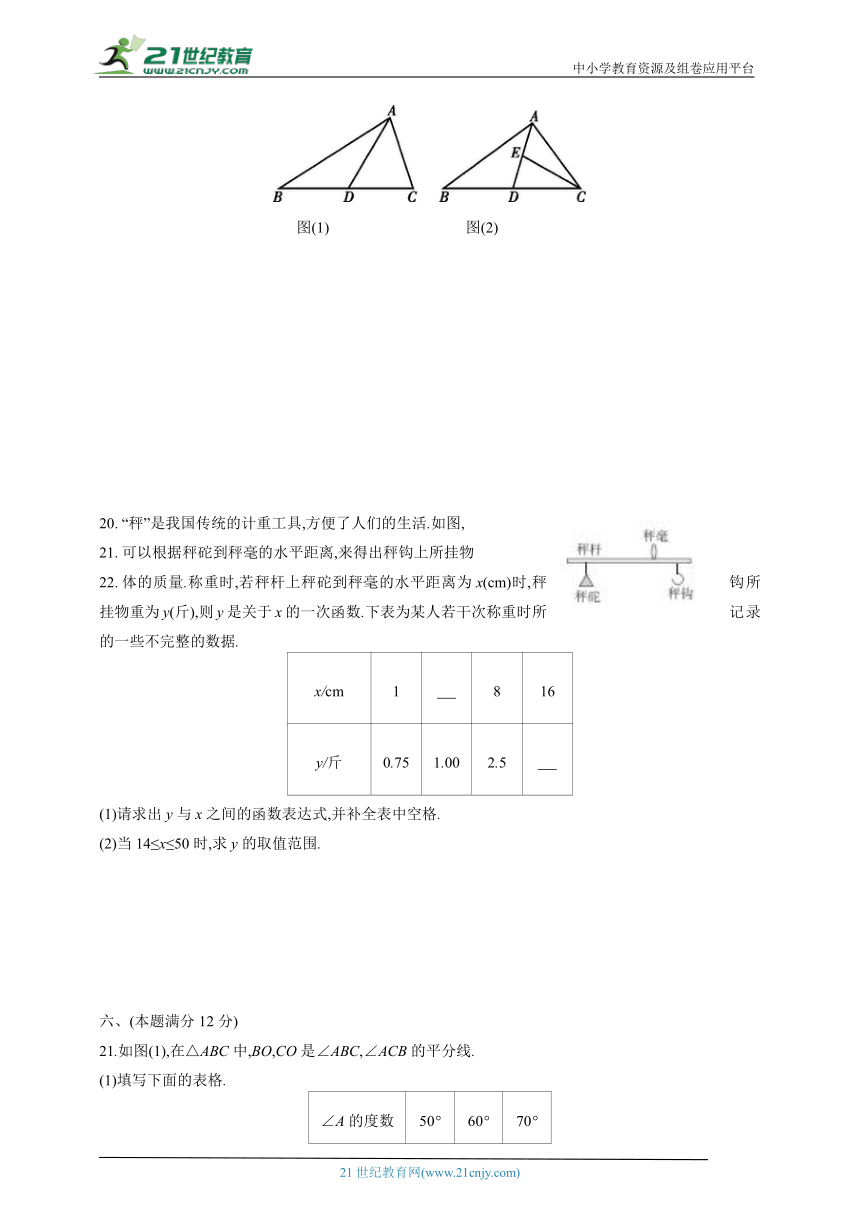
19.如图(1),在△ABC中,AD是BC边上的中线,AB>AC,△ABD和△ADC的周长之差为2,且AB与AC的和为14.
(1)求AB和AC的长;
(2)如图(2),若∠BAC=90°,E是AD的中点,连接CE,求△CDE的面积.
图(1) 图(2)
“秤”是我国传统的计重工具,方便了人们的生活.如图,
可以根据秤砣到秤毫的水平距离,来得出秤钩上所挂物
体的质量.称重时,若秤杆上秤砣到秤毫的水平距离为x(cm)时,秤钩所挂物重为y(斤),则y是关于x的一次函数.下表为某人若干次称重时所记录的一些不完整的数据.
x/cm 1 8 16
y/斤 0.75 1.00 2.5
(1)请求出y与x之间的函数表达式,并补全表中空格.
(2)当14≤x≤50时,求y的取值范围.
六、(本题满分12分)
21.如图(1),在△ABC中,BO,CO是∠ABC,∠ACB的平分线.
(1)填写下面的表格.
∠A的度数 50° 60° 70°
∠BOC的度数
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想.
(3)如图(2),△ABC的高BE,CD交于点O,试说明图中∠A与∠BOD之间的数量关系.
图(1) 图(2)
七、(本题满分12分)
22.阅读理解:在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;
若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.
例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
已知点A(-,0),B为y轴上的一个动点.
(1)若点B(0,3),则点A与点B的“非常距离”为 ;
(2)若点A与点B的“非常距离”为2,求出点B的坐标;
(3)点A与点B的“非常距离”的最小值为 .
八、(本题满分14分)
23.某电脑经销商,今年八、九月份销售A型和B型电脑的情况如下表.
A型电脑/台 B型电脑/台 总利润/元
八月份 15 20 4 500
九月份 20 10 3 500
(1)求每台A型电脑和B型电脑的销售利润.
(2)该商店计划购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.求该商店购进A型、B型电脑各多少台,才能使销售总利润最大.
(3)实际进货时,厂家对A型电脑出厂价下调m(0八年级上学期期中综合测评卷
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
C B A A B C C A D D
11.(1,-2)(答案不唯一) 12.75
13. 14.(1)b<0 (2)-8或-24
1.C 【易错】易忽略m≠0的条件
2.B 3.A 4.A
5.B 根据题意得a-3=0,b-7=0解得a=3,b=7.因为c是最大边长,所以 76.C 由题意得1-a=2-3,-3-1=-1+b,∴a=2,b=-3,∴a-b=5.
7.C 由题意易得,正比例函数的表达式为y=x.设正比例函数平移后的函数表达式为y=x+b,把点(1,-1)代入y=x+b,得-1=+b,解得 b=-,∴平移后的函数表达式为y=x-,∴函数图象大致为
.
8.A
图示速解
如图,∵A(-1,2),∴A在第二象限,∴原点在点A的右方1个单位,下方2个单位处.
∵B(2,-4),∴点B在第四象限,∴原点在点B的左方2个单位,上方4个单位处,由此可知点O1为坐标原点.
9.D
10.D 根据题意,得A1(2,4),A2(-3,3),A3(-2,-2),A4(3,-1),A5(2,4),A6(-3,3),….可以发现,每4个点为一个循环周期.∵2 023÷4=505……3,∴点的坐标与点A3的坐标相同,为(-2,-2).故选D.
11.(1,-2)【答案不唯一,或(1,-1),(2,-1)等】
图示速解 所有符合条件的点P如图所示.
12.75 【技巧】结合三角形外角和三角板的特殊角度求解
13.
14.(1)b<0 (2)-8或-24 (1)∵一次函数y=kx+b的图象交y轴于负半轴,∴b<0.
(2)(分类讨论思想)①当k>0时,y随x的增大而增大,∴当x=0时,y=-2,当x=2时,y=6,代入y=kx+b,得解得
∴kb=4×(-2)=-8.②当k<0时,y随x的增大而减小,∴当x=0时,y=6,当x=2时,y=-2,代入y=kx+b,得解得
∴kb=-4×6=-24.综上,kb的值为-8或-24.
15.【参考答案】(1)k=9.
【提示】将原点(0,0)代入即可(4分)
(2)当k>3时,y随x的增大而减小. (8分)
16.【参考答案】(1)∵点P(2a+3,a-1),点P的纵坐标比横坐标大3,
∴a-1-(2a+3)=3,解得a=-7.
∵2a+3=-11,a-1=-8,
∴点P的坐标为(-11,-8). (4分)
(2)∵点P在过点A(2,-3)且与x轴平行的直线上,∴a-1=-3,解得a=-2.
∵2a+3=-1,∴点P的坐标为(-1,-3).(8分)
17.【参考答案】(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°-30°-70°=80°.
又AE平分∠BAC,
∴∠CAF=∠CAB=×80°=40°. (4分)
(2)∵CD为△ABC的高,∠CAD=80°,
∴∠ACD=10°,
∴∠AFC=180°-∠ACF-∠CAF=180°-10°-40°=130°. (8分)
18.【参考答案】(1)(-3,0) (1,3) (3,1) (6分)
(2)若“馬”的位置在C点,为了到达D点,则所走路线可以为(1,3)→(2,1)→(3,3)→(1,2)→(3,1)(答案不唯一,正确即可得分). (8分)
19.【参考答案】(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长-△ADC的周长=(AB+AD+BD)-(AC+AD+CD)=AB-AC=2. (2分)
又AB+AC=14,∴AB=8,
∴AC=14-AB=6. (5分)
(2)∵∠BAC=90°,AB=8,AC=6,
∴S△ABC=AB·AC=×8×6=24. (7分)
∵AD是BC边上的中线,E为AD的中点,
∴S△ACD=S△ABC,S△CDE=S△ACD,
∴S△CDE=S△ABC=×24=6. (10分)
20.【参考答案】(1)设y与x之间的函数表达式为y=kx+b.
由题表可知,当x=1时,y=0.75,当x=8时,y=2.5,
∴解得
即y与x之间的函数表达式为y=0.25x+0.5. (3分)
计算易得空格从上到下分别为2,4.5. (5分)
(2)由(1)可知y=0.25x+0.5,k=0.25>0,
∴y随x的增大而增大.
令x=14,得y=4.令x=50,得y=13,
∴y的取值范围是4≤y≤13. (10分)
21.【参考答案】(1)填表如下: (3分)
∠A的度数 50° 60° 70°
∠BOC的度数 115° 120° 125°
(2)猜想:∠BOC=90°+∠A.
证明:∵在△ABC中,BO,CO是∠ABC,∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB.
∵∠ABC+∠ACB=180°-∠A,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=90°-∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-∠A)=90°+∠A. (8分)
(3)∠A=∠BOD.
证明:∵△ABC的高BE,CD交于点O,
∴∠BDC=∠BEA=90°,
∴∠ABE+∠BOD=90°,∠ABE+∠A=90°,
∴∠A=∠BOD. (12分)
22.【参考答案】(1)3 (3分)
(2)∵B为y轴上的一个动点,
∴设点B的坐标为(0,b).
∵|--0|=≠2,∴|0-b|=2,
解得b=2或b=-2,
∴点B的坐标是(0,2)或(0,-2). (9分)
(3) (12分)
23.【参考答案】(1)设每台A型电脑的销售利润是a元,每台B型电脑的销售利润是b元,根据题意可得解得
答:每台A型电脑的销售利润是100元,每台B型电脑的销售利润是150元. (3分)
(2)由购进A型电脑x台,得购进B型电脑(100-x)台,
由题意得y=100x+150(100-x)=-50x+15 000.
∵B型电脑的进货量不超过A型电脑的2倍,
∴100-x≤2x,解得x≥33.
∵y=-50x+15 000,x为正整数,
∴y随x的增大而减小,
∴当x=34时,y取最大值,100-x=66.
答:商店购进34台A型电脑和66台B型电脑,才能使销售总利润最大. (8分)
(3)设这100台电脑的销售总利润为w元,
根据题意得w=(100+m)x+150(100-x)=(m-50)x+15 000,
∵销售B型电脑的利润不低于9 000元,
∴150(100-x)≥9 000,解得x≤40,
∴33≤x≤40.
∵0∴x=34时,w取得最大值,
即商店购进34台A型电脑和66台B型电脑的销售利润最大. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024沪科版八年级数学上学期单元测试卷
八年级上学期期中综合测评卷
时间:120分钟 满分:150分
一、选择题(本大题共10小题,每小题4分,满分40分.每小题有四个选项,其中只有一个选项符合题意)
1.若y=mx|m-1|是正比例函数,则m的值是 ( )
A.0 B.1 C.2 D.0或-2
2.三角形的一个外角小于与它相邻的内角,这个三角形是 ( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不确定
3.已知点A(m,n)在第三象限,则点B(|m|,-n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.下列选项中,可以用来证明命题“若a2>4,则a>2”是假命题的反例是 ( )
A.a=-3 B.a=-2 C.a=2 D.a=3
5.已知三角形三边长分别为a,b,c,其中a,b满足|a-3|+(b-7)2=0,那么这个三角形的最大边长c的值可以是 ( )
A.10 B.8 C.5 D.6
6.已知点A(1,-3),点B(2,-1),将线段AB平移至A1B1.若点A1(a,1),点B1(3,-b),则a-b的值为 ( )
A.1 B.-1 C.5 D.-5
7.已知正比例函数y=kx(k≠0)的图象过点(-2,-3),把正比例函数的图象平移,使它过点(1,-1),则平移后的函数图象大致是 ( )
8.如图,直线m⊥n,在平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(-1,2),点B的坐标为(2,-4),则坐标原点为 ( )
A.O1 B.O2 C.O3 D.O4
(第8题) (第9题)
9.某通讯公司就上宽带网推出A,B,C三种月收费方式,这三种收费方式每月所需的费用y(元)与上网时间x(h)之间的函数关系如图所示,则下列判断错误的是 ( )
A.每月上网时间不足25 h时,选择A方式最省钱
B.每月上网费用为60元时,B方式可上网的时间比A方式多
C.每月上网费用为120元时,选择C方式上网的时间最长
D.每月上网时间为50 h时,选择A方式最省钱
10.在平面直角坐标系中,对于点P(x,y),我们把点P'(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.若点A1的坐标为(2,4),则点A2 023的坐标为( )
A.(-3,3) B.(2,4) C.(3,-1) D.(-2,-2)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),写出一个符合上述条件的点P的坐标: .
12.将一副直角三角尺按如图所示的方式摆放,则∠α= °.
(第12题) (第13题)
13.如图,直线y=kx+b(k≠0)与y=-x+相交于点(2,m),则关于x,y的方程组的解是 .
14.已知一次函数y=kx+b.
(1)若该函数图象交y轴于负半轴,则b的取值范围是 .
(2)当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤6,则kb的值为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14.(1) (2)
三、(本大题共2小题,每小题8分,满分16分)
15.已知一次函数y=(3-k)x-2k+18.
(1)当k为何值时,这个一次函数的图象经过原点
(2)当k为何值时,y随x的增大而减小
16.已知点P(2a+3,a-1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3.
(2)点P在过点A(2,-3)且与x轴平行的直线上.
四、(本大题共2小题,每小题8分,满分16分)
17.如图所示,AE为△ABC的角平分线,CD为△ABC的高.若∠B=30°,∠ACB=70°.
(1)求∠CAF的度数.
(2)求∠AFC的度数.
18.象棋在中国有近三千年的历史,中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“馬”走的规则是沿“日”形的对角线走.例如:图中“馬”由所在的位置可以直接走到点A,B处.
(1)若“帥”位于点(0,0),“相”位于点(4,2),则“馬”所在的点的坐标为 ,点C的坐标为 ,点D的坐标为 .
(2)若“馬”的位置在C点,为了到达D点,请按“馬”走的规则,写出一种你认为合理的行走路线(用坐标表示).
五、(本大题共2小题,每小题10分,满分20分)
19.如图(1),在△ABC中,AD是BC边上的中线,AB>AC,△ABD和△ADC的周长之差为2,且AB与AC的和为14.
(1)求AB和AC的长;
(2)如图(2),若∠BAC=90°,E是AD的中点,连接CE,求△CDE的面积.
图(1) 图(2)
“秤”是我国传统的计重工具,方便了人们的生活.如图,
可以根据秤砣到秤毫的水平距离,来得出秤钩上所挂物
体的质量.称重时,若秤杆上秤砣到秤毫的水平距离为x(cm)时,秤钩所挂物重为y(斤),则y是关于x的一次函数.下表为某人若干次称重时所记录的一些不完整的数据.
x/cm 1 8 16
y/斤 0.75 1.00 2.5
(1)请求出y与x之间的函数表达式,并补全表中空格.
(2)当14≤x≤50时,求y的取值范围.
六、(本题满分12分)
21.如图(1),在△ABC中,BO,CO是∠ABC,∠ACB的平分线.
(1)填写下面的表格.
∠A的度数 50° 60° 70°
∠BOC的度数
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想.
(3)如图(2),△ABC的高BE,CD交于点O,试说明图中∠A与∠BOD之间的数量关系.
图(1) 图(2)
七、(本题满分12分)
22.阅读理解:在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;
若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.
例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
已知点A(-,0),B为y轴上的一个动点.
(1)若点B(0,3),则点A与点B的“非常距离”为 ;
(2)若点A与点B的“非常距离”为2,求出点B的坐标;
(3)点A与点B的“非常距离”的最小值为 .
八、(本题满分14分)
23.某电脑经销商,今年八、九月份销售A型和B型电脑的情况如下表.
A型电脑/台 B型电脑/台 总利润/元
八月份 15 20 4 500
九月份 20 10 3 500
(1)求每台A型电脑和B型电脑的销售利润.
(2)该商店计划购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.求该商店购进A型、B型电脑各多少台,才能使销售总利润最大.
(3)实际进货时,厂家对A型电脑出厂价下调m(0
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
C B A A B C C A D D
11.(1,-2)(答案不唯一) 12.75
13. 14.(1)b<0 (2)-8或-24
1.C 【易错】易忽略m≠0的条件
2.B 3.A 4.A
5.B 根据题意得a-3=0,b-7=0解得a=3,b=7.因为c是最大边长,所以 7
7.C 由题意易得,正比例函数的表达式为y=x.设正比例函数平移后的函数表达式为y=x+b,把点(1,-1)代入y=x+b,得-1=+b,解得 b=-,∴平移后的函数表达式为y=x-,∴函数图象大致为
.
8.A
图示速解
如图,∵A(-1,2),∴A在第二象限,∴原点在点A的右方1个单位,下方2个单位处.
∵B(2,-4),∴点B在第四象限,∴原点在点B的左方2个单位,上方4个单位处,由此可知点O1为坐标原点.
9.D
10.D 根据题意,得A1(2,4),A2(-3,3),A3(-2,-2),A4(3,-1),A5(2,4),A6(-3,3),….可以发现,每4个点为一个循环周期.∵2 023÷4=505……3,∴点的坐标与点A3的坐标相同,为(-2,-2).故选D.
11.(1,-2)【答案不唯一,或(1,-1),(2,-1)等】
图示速解 所有符合条件的点P如图所示.
12.75 【技巧】结合三角形外角和三角板的特殊角度求解
13.
14.(1)b<0 (2)-8或-24 (1)∵一次函数y=kx+b的图象交y轴于负半轴,∴b<0.
(2)(分类讨论思想)①当k>0时,y随x的增大而增大,∴当x=0时,y=-2,当x=2时,y=6,代入y=kx+b,得解得
∴kb=4×(-2)=-8.②当k<0时,y随x的增大而减小,∴当x=0时,y=6,当x=2时,y=-2,代入y=kx+b,得解得
∴kb=-4×6=-24.综上,kb的值为-8或-24.
15.【参考答案】(1)k=9.
【提示】将原点(0,0)代入即可(4分)
(2)当k>3时,y随x的增大而减小. (8分)
16.【参考答案】(1)∵点P(2a+3,a-1),点P的纵坐标比横坐标大3,
∴a-1-(2a+3)=3,解得a=-7.
∵2a+3=-11,a-1=-8,
∴点P的坐标为(-11,-8). (4分)
(2)∵点P在过点A(2,-3)且与x轴平行的直线上,∴a-1=-3,解得a=-2.
∵2a+3=-1,∴点P的坐标为(-1,-3).(8分)
17.【参考答案】(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°-30°-70°=80°.
又AE平分∠BAC,
∴∠CAF=∠CAB=×80°=40°. (4分)
(2)∵CD为△ABC的高,∠CAD=80°,
∴∠ACD=10°,
∴∠AFC=180°-∠ACF-∠CAF=180°-10°-40°=130°. (8分)
18.【参考答案】(1)(-3,0) (1,3) (3,1) (6分)
(2)若“馬”的位置在C点,为了到达D点,则所走路线可以为(1,3)→(2,1)→(3,3)→(1,2)→(3,1)(答案不唯一,正确即可得分). (8分)
19.【参考答案】(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长-△ADC的周长=(AB+AD+BD)-(AC+AD+CD)=AB-AC=2. (2分)
又AB+AC=14,∴AB=8,
∴AC=14-AB=6. (5分)
(2)∵∠BAC=90°,AB=8,AC=6,
∴S△ABC=AB·AC=×8×6=24. (7分)
∵AD是BC边上的中线,E为AD的中点,
∴S△ACD=S△ABC,S△CDE=S△ACD,
∴S△CDE=S△ABC=×24=6. (10分)
20.【参考答案】(1)设y与x之间的函数表达式为y=kx+b.
由题表可知,当x=1时,y=0.75,当x=8时,y=2.5,
∴解得
即y与x之间的函数表达式为y=0.25x+0.5. (3分)
计算易得空格从上到下分别为2,4.5. (5分)
(2)由(1)可知y=0.25x+0.5,k=0.25>0,
∴y随x的增大而增大.
令x=14,得y=4.令x=50,得y=13,
∴y的取值范围是4≤y≤13. (10分)
21.【参考答案】(1)填表如下: (3分)
∠A的度数 50° 60° 70°
∠BOC的度数 115° 120° 125°
(2)猜想:∠BOC=90°+∠A.
证明:∵在△ABC中,BO,CO是∠ABC,∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB.
∵∠ABC+∠ACB=180°-∠A,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=90°-∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-∠A)=90°+∠A. (8分)
(3)∠A=∠BOD.
证明:∵△ABC的高BE,CD交于点O,
∴∠BDC=∠BEA=90°,
∴∠ABE+∠BOD=90°,∠ABE+∠A=90°,
∴∠A=∠BOD. (12分)
22.【参考答案】(1)3 (3分)
(2)∵B为y轴上的一个动点,
∴设点B的坐标为(0,b).
∵|--0|=≠2,∴|0-b|=2,
解得b=2或b=-2,
∴点B的坐标是(0,2)或(0,-2). (9分)
(3) (12分)
23.【参考答案】(1)设每台A型电脑的销售利润是a元,每台B型电脑的销售利润是b元,根据题意可得解得
答:每台A型电脑的销售利润是100元,每台B型电脑的销售利润是150元. (3分)
(2)由购进A型电脑x台,得购进B型电脑(100-x)台,
由题意得y=100x+150(100-x)=-50x+15 000.
∵B型电脑的进货量不超过A型电脑的2倍,
∴100-x≤2x,解得x≥33.
∵y=-50x+15 000,x为正整数,
∴y随x的增大而减小,
∴当x=34时,y取最大值,100-x=66.
答:商店购进34台A型电脑和66台B型电脑,才能使销售总利润最大. (8分)
(3)设这100台电脑的销售总利润为w元,
根据题意得w=(100+m)x+150(100-x)=(m-50)x+15 000,
∵销售B型电脑的利润不低于9 000元,
∴150(100-x)≥9 000,解得x≤40,
∴33≤x≤40.
∵0
即商店购进34台A型电脑和66台B型电脑的销售利润最大. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
