13.1.1 轴对称同步讲练(含答案)
图片预览


文档简介
13.1 轴对称
第1课时 轴对称
【知识重点】
知识点1 轴对称图形
定义 如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴. 我们也说这个图形关于这条直线(成轴)对称.
特别解读
轴对称图形的三个条件:1. 一个整体图形. 2. 一条直线——对称轴. 3. 直线两旁的部分完全重合.
温馨提示
1. 轴对称图形是一个图形自身的特性,它被对称轴分成的两部分能够互相重合,其对称点在同一图形上.
2. 对称轴是一条直线,而不是射线或线段.
3. 一个轴对称图形的对称轴可能有1 条,也可能有多条,还可能有无数条.
知识点2 轴对称
1. 定义 把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
特别解读
●轴对称的三个条件:1. 有两个图形;2. 存在一条直线;3. 一个图形沿着这条直线折叠后与另一个图形重合.
●轴对称的两个特性:
1. 成轴对称的两个图形全等. 但全等的两个图形不一定成轴对称. 2. 轴对称是图形的一种全等变换.
2. 轴对称与轴对称图形的区别与联系
知识点3 成轴对称和轴对称图形的性质
1. 成轴对称的性质 如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线,如图所示.
特别地:成轴对称的两个图形的对应线段所在直线平行或者重合或者相交于某一点,且该点一定在对称轴上.
2. 经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
3. 轴对称图形的性质 轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线,
如图所示.
特别解读
1. 轴对称图形或成轴对称的两个图形的对应线段、对应角相等;
2. 轴对称图形被对称轴分成的两部分全等,并且这两部分关于对称轴成轴对称. 成轴对称的两个图形也全等,但全等的两个图形不一定成轴对称.
【经典例题】
【例1】如图,下列交通标志中,是轴对称图形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
解题秘方:根据轴对称图形的定义识别.
归纳:判断轴对称图形的方法
根据图形的特征,如果能找到一条直线,沿着这条直线折叠,直线两旁的部分能够互相重合,即可确定这个图形是轴对称图形,否则就不是轴对称图形.
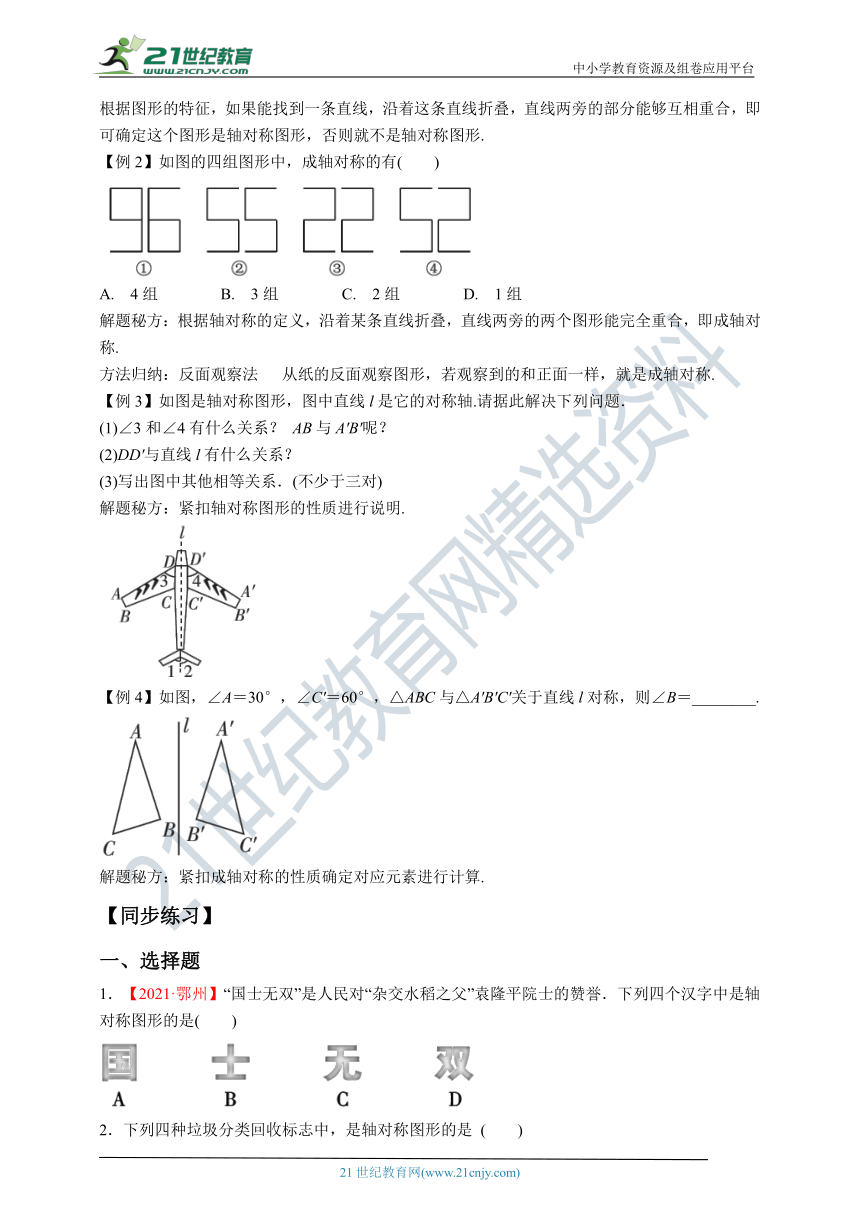
【例2】如图的四组图形中,成轴对称的有( )
A. 4组 B. 3组 C. 2组 D. 1组
解题秘方:根据轴对称的定义,沿着某条直线折叠,直线两旁的两个图形能完全重合,即成轴对称.
方法归纳:反面观察法 从纸的反面观察图形,若观察到的和正面一样,就是成轴对称.
【例3】如图是轴对称图形,图中直线l是它的对称轴.请据此解决下列问题.
(1)∠3和∠4有什么关系? AB与A′B′呢?
(2)DD′与直线l有什么关系?
(3)写出图中其他相等关系.(不少于三对)
解题秘方:紧扣轴对称图形的性质进行说明.
【例4】如图,∠A=30°,∠C′=60°,△ABC与△A′B′C′关于直线l对称,则∠B=________.
解题秘方:紧扣成轴对称的性质确定对应元素进行计算.
【同步练习】
一、选择题
1.【2021·鄂州】“国士无双”是人民对“杂交水稻之父”袁隆平院士的赞誉.下列四个汉字中是轴对称图形的是( )
2.下列四种垃圾分类回收标志中,是轴对称图形的是 ( )
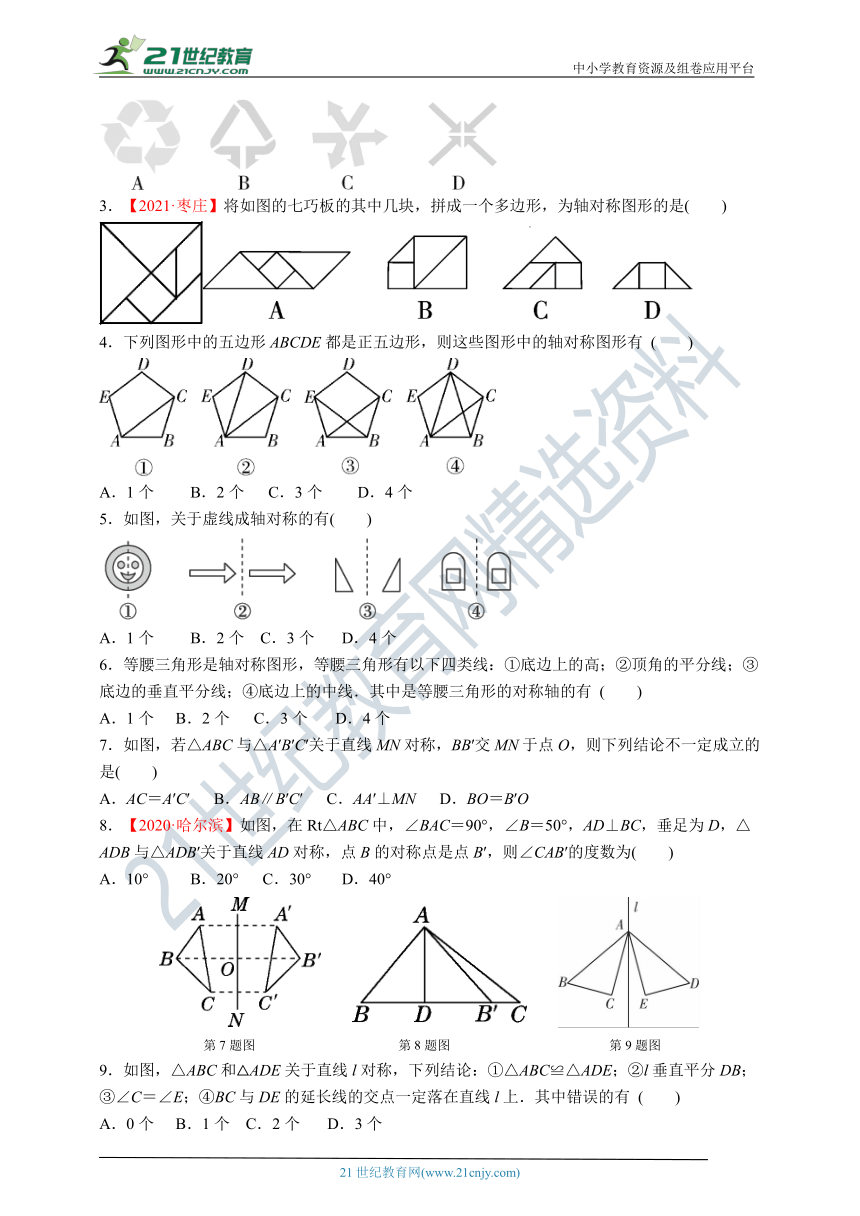
3.【2021·枣庄】将如图的七巧板的其中几块,拼成一个多边形,为轴对称图形的是( )
4.下列图形中的五边形ABCDE都是正五边形,则这些图形中的轴对称图形有 ( )
A.1个 B.2个 C.3个 D.4个
5.如图,关于虚线成轴对称的有( )
A.1个 B.2个 C.3个 D.4个
6.等腰三角形是轴对称图形,等腰三角形有以下四类线:①底边上的高;②顶角的平分线;③底边的垂直平分线;④底边上的中线.其中是等腰三角形的对称轴的有 ( )
A.1个 B.2个 C.3个 D.4个
7.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定成立的是( )
A.AC=A′C′ B.AB∥B′C′ C.AA′⊥MN D.BO=B′O
8.【2020·哈尔滨】如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为( )
A.10° B.20° C.30° D.40°
第7题图 第8题图 第9题图
9.如图,△ABC和△ADE关于直线l对称,下列结论:①△ABC≌△ADE;②l垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上.其中错误的有 ( )
A.0个 B.1个 C.2个 D.3个
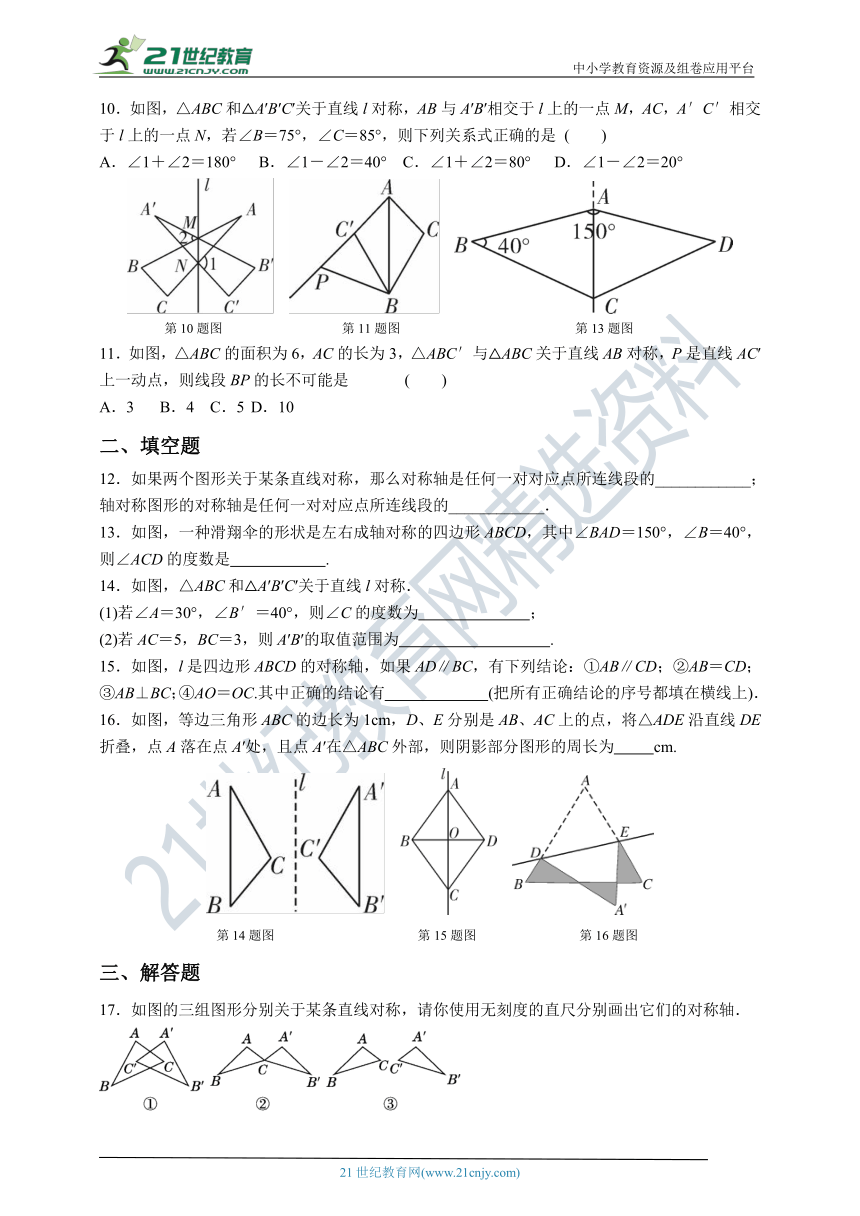
10.如图,△ABC和△A′B′C′关于直线l对称,AB与A′B′相交于l上的一点M,AC,A′C′相交于l上的一点N,若∠B=75°,∠C=85°,则下列关系式正确的是 ( )
A.∠1+∠2=180° B.∠1-∠2=40° C.∠1+∠2=80° D.∠1-∠2=20°
第10题图 第11题图 第13题图
11.如图,△ABC的面积为6,AC的长为3,△ABC′与△ABC关于直线AB对称,P是直线AC′上一动点,则线段BP的长不可能是 ( )
A.3 B.4 C.5 D.10
二、填空题
12.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的____________;轴对称图形的对称轴是任何一对对应点所连线段的____________.
13.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠ACD的度数是 .
14.如图,△ABC和△A′B′C′关于直线l对称.
(1)若∠A=30°,∠B′=40°,则∠C的度数为 ;
(2)若AC=5,BC=3,则A′B′的取值范围为 .
15.如图,l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=CD;③AB⊥BC;④AO=OC.其中正确的结论有 (把所有正确结论的序号都填在横线上).
16.如图,等边三角形ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 cm.
第14题图 第15题图 第16题图
三、解答题
17.如图的三组图形分别关于某条直线对称,请你使用无刻度的直尺分别画出它们的对称轴.
18.如图的阴影三角形与哪些三角形分别成轴对称?整个图形是轴对称图形吗?如果是,它共有几条对称轴?
19.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
20.【教学运算】如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4 cm,FC=1 cm,∠BAC=76°,∠EAC=58°.
(1)求BF的长度;
(2)求∠CAD的度数;
(3)连接EC,线段EC与直线MN有什么关系?并说明理由.
21.如图,已知△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)若直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹角α的数量关系.
22.如图,在直线MN上求作一点P,使∠MPA=∠NPB.(要求:写出作法)
23.如图,P是△ABC内一点,点D,E,F分别是点P关于直线AB,BC,CA的对称点,求∠ADB+∠BEC+∠CFA的度数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,下列交通标志中,是轴对称图形的有( A )
A. 1个 B. 2个 C. 3个 D. 4个
解题秘方:根据轴对称图形的定义识别.
归纳:判断轴对称图形的方法
根据图形的特征,如果能找到一条直线,沿着这条直线折叠,直线两旁的部分能够互相重合,即可确定这个图形是轴对称图形,否则就不是轴对称图形.
【例2】如图的四组图形中,成轴对称的有( D )
A. 4组 B. 3组 C. 2组 D. 1组
解题秘方:根据轴对称的定义,沿着某条直线折叠,直线两旁的两个图形能完全重合,即成轴对称.
解:根据轴对称的定义,可以判断只有④中的两个图形沿着某一条直线折叠后,两个图形能够重合,所以成轴对称的只有1组.
方法归纳:反面观察法 从纸的反面观察图形,若观察到的和正面一样,就是成轴对称.
【例3】如图是轴对称图形,图中直线l是它的对称轴.请据此解决下列问题.
解题秘方:紧扣轴对称图形的性质进行说明.
(1)∠3和∠4有什么关系? AB与A′B′呢?
解:∠3=∠4, AB=A′B′.
(2)DD′与直线l有什么关系?
直线l是DD′的垂直平分线.
(3)写出图中其他相等关系.(不少于三对)
AD=A′D′,∠1=∠2,DC=D′C′.(答案不唯一)
【例4】如图,∠A=30°,∠C′=60°,△ABC与△A′B′C′关于直线l对称,则∠B=________.
解题秘方:紧扣成轴对称的性质确定对应元素进行计算.
解:∵△ ABC与△A′B′C′关于直线l对称,∠C′=60°,
∴∠C=∠C′=60°,
在△ABC中,
∠B=180°-∠A-∠C=180°-30°-60°=90°.
【同步练习】
一、选择题
1.【2021·鄂州】“国士无双”是人民对“杂交水稻之父”袁隆平院士的赞誉.下列四个汉字中是轴对称图形的是( B )
2.下列四种垃圾分类回收标志中,是轴对称图形的是 ( D )
3.【2021·枣庄】将如图的七巧板的其中几块,拼成一个多边形,为轴对称图形的是( D )
4.下列图形中的五边形ABCDE都是正五边形,则这些图形中的轴对称图形有 ( D )
A.1个 B.2个 C.3个 D.4个
5.如图,关于虚线成轴对称的有( C )
A.1个 B.2个 C.3个 D.4个
6.等腰三角形是轴对称图形,等腰三角形有以下四类线:①底边上的高;②顶角的平分线;③底边的垂直平分线;④底边上的中线.其中是等腰三角形的对称轴的有 ( A )
A.1个 B.2个 C.3个 D.4个
7.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定成立的是( B )
A.AC=A′C′ B.AB∥B′C′ C.AA′⊥MN D.BO=B′O
8.【2020·哈尔滨】如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为( A )
A.10° B.20° C.30° D.40°
第7题图 第8题图 第9题图
9.如图,△ABC和△ADE关于直线l对称,下列结论:①△ABC≌△ADE;②l垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上.其中错误的有 ( A )
A.0个 B.1个 C.2个 D.3个
10.如图,△ABC和△A′B′C′关于直线l对称,AB与A′B′相交于l上的一点M,AC,A′C′相交于l上的一点N,若∠B=75°,∠C=85°,则下列关系式正确的是 ( B )
A.∠1+∠2=180° B.∠1-∠2=40° C.∠1+∠2=80° D.∠1-∠2=20°
第10题图 第11题图 第13题图
11.如图,△ABC的面积为6,AC的长为3,△ABC′与△ABC关于直线AB对称,P是直线AC′上一动点,则线段BP的长不可能是 ( A )
A.3 B.4 C.5 D.10
二、填空题
12.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的____________;轴对称图形的对称轴是任何一对对应点所连线段的____________.
【答案】垂直平分线 垂直平分线
13.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠ACD的度数是 .
【答案】65°
14.如图,△ABC和△A′B′C′关于直线l对称.
(1)若∠A=30°,∠B′=40°,则∠C的度数为 ;
(2)若AC=5,BC=3,则A′B′的取值范围为 .
【答案】110° 2<A′B′<8
15.如图,l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=CD;③AB⊥BC;④AO=OC.其中正确的结论有 (把所有正确结论的序号都填在横线上).
【答案】①②④
16.如图,等边三角形ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 cm.
【答案】3
第14题图 第15题图 第16题图
三、解答题
17.如图的三组图形分别关于某条直线对称,请你使用无刻度的直尺分别画出它们的对称轴.
解:如图.
18.如图的阴影三角形与哪些三角形分别成轴对称?整个图形是轴对称图形吗?如果是,它共有几条对称轴?
解:题图中的阴影三角形与三角形2,3,4分别成轴对称.整个图形是轴对称图形.它共有4条对称轴.
19.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在G处,EF为折痕.
(1)求证:△FGC≌△EBC;
证明:由题意知
∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,
∴∠GCF=∠BCE.
∵∠G=∠D=∠B=90°,GC=AD=BC,
∴△FGC≌△EBC(ASA).
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
解:∵△FGC≌△EBC,∴GF=BE.
∵DF=GF,∴DF=BE.
∴四边形ECGF的面积=四边形AEFD的面积
=====16.
20.【教学运算】如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4 cm,FC=1 cm,∠BAC=76°,∠EAC=58°.
(1)求BF的长度;
解:∵△ABC与△ADE关于直线MN对称,ED=4 cm,
∴BC=ED=4 cm.
∵FC=1 cm,
∴BF=BC-FC=4-1=3(cm).
(2)求∠CAD的度数;
解:∵△ABC与△ADE关于直线MN对称,
∠BAC=76°,∴∠EAD=∠BAC=76°.
∵∠EAC=58°,
∴∠CAD=∠EAD-∠EAC=76°-58°=18°.
(3)连接EC,线段EC与直线MN有什么关系?并说明理由.
解:直线MN垂直平分线段EC.理由如下:
∵E,C关于直线MN对称,
∴直线MN垂直平分线段EC.
21.如图,已知△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
解:如图,连接B′B″,
画线段B′B″的垂直平分线EF,
则直线EF是△A′B′C′和△A″B″C″的对称轴.
(2)若直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹角α的数量关系.
解:如图,连接B′O.
∵△ABC和△A′B′C′关于直线MN对称,
∴∠BOM=∠B′OM.
∵△A′B′C′和△A″B″C″关于直线EF对称,
∴∠B′OE=∠B″OE.
∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE
=2(∠B′OM+∠B′OE)=2∠MOE,即∠BOB″=2α.
22.如图,在直线MN上求作一点P,使∠MPA=∠NPB.(要求:写出作法)
【思路点拨】在直线MN上求作一点P,使∠MPA=∠NPB,其实质是利用轴对称的性质在直线上找一点P使它到点A,B的距离之和最小.
解:①作点A关于直线MN的对称点A′;②连接BA′交直线MN于点P,连接AP,则∠MPA=∠NPB.
如图所示.
23.如图,P是△ABC内一点,点D,E,F分别是点P关于直线AB,BC,CA的对称点,求∠ADB+∠BEC+∠CFA的度数.
解:连接PA,PC.
∵点P,D关于直线AB对称,
∴AP=AD,BP=BD.
在△APB和△ADB中,
∴△APB≌△ADB(SSS).∴∠APB=∠ADB.
同理可证:∠BPC=∠BEC,∠APC=∠AFC.
∴∠ADB+∠BEC+∠CFA
=∠APB+∠BPC+∠APC
=360°.
第1课时 轴对称
【知识重点】
知识点1 轴对称图形
定义 如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴. 我们也说这个图形关于这条直线(成轴)对称.
特别解读
轴对称图形的三个条件:1. 一个整体图形. 2. 一条直线——对称轴. 3. 直线两旁的部分完全重合.
温馨提示
1. 轴对称图形是一个图形自身的特性,它被对称轴分成的两部分能够互相重合,其对称点在同一图形上.
2. 对称轴是一条直线,而不是射线或线段.
3. 一个轴对称图形的对称轴可能有1 条,也可能有多条,还可能有无数条.
知识点2 轴对称
1. 定义 把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
特别解读
●轴对称的三个条件:1. 有两个图形;2. 存在一条直线;3. 一个图形沿着这条直线折叠后与另一个图形重合.
●轴对称的两个特性:
1. 成轴对称的两个图形全等. 但全等的两个图形不一定成轴对称. 2. 轴对称是图形的一种全等变换.
2. 轴对称与轴对称图形的区别与联系
知识点3 成轴对称和轴对称图形的性质
1. 成轴对称的性质 如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线,如图所示.
特别地:成轴对称的两个图形的对应线段所在直线平行或者重合或者相交于某一点,且该点一定在对称轴上.
2. 经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
3. 轴对称图形的性质 轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线,
如图所示.
特别解读
1. 轴对称图形或成轴对称的两个图形的对应线段、对应角相等;
2. 轴对称图形被对称轴分成的两部分全等,并且这两部分关于对称轴成轴对称. 成轴对称的两个图形也全等,但全等的两个图形不一定成轴对称.
【经典例题】
【例1】如图,下列交通标志中,是轴对称图形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
解题秘方:根据轴对称图形的定义识别.
归纳:判断轴对称图形的方法
根据图形的特征,如果能找到一条直线,沿着这条直线折叠,直线两旁的部分能够互相重合,即可确定这个图形是轴对称图形,否则就不是轴对称图形.
【例2】如图的四组图形中,成轴对称的有( )
A. 4组 B. 3组 C. 2组 D. 1组
解题秘方:根据轴对称的定义,沿着某条直线折叠,直线两旁的两个图形能完全重合,即成轴对称.
方法归纳:反面观察法 从纸的反面观察图形,若观察到的和正面一样,就是成轴对称.
【例3】如图是轴对称图形,图中直线l是它的对称轴.请据此解决下列问题.
(1)∠3和∠4有什么关系? AB与A′B′呢?
(2)DD′与直线l有什么关系?
(3)写出图中其他相等关系.(不少于三对)
解题秘方:紧扣轴对称图形的性质进行说明.
【例4】如图,∠A=30°,∠C′=60°,△ABC与△A′B′C′关于直线l对称,则∠B=________.
解题秘方:紧扣成轴对称的性质确定对应元素进行计算.
【同步练习】
一、选择题
1.【2021·鄂州】“国士无双”是人民对“杂交水稻之父”袁隆平院士的赞誉.下列四个汉字中是轴对称图形的是( )
2.下列四种垃圾分类回收标志中,是轴对称图形的是 ( )
3.【2021·枣庄】将如图的七巧板的其中几块,拼成一个多边形,为轴对称图形的是( )
4.下列图形中的五边形ABCDE都是正五边形,则这些图形中的轴对称图形有 ( )
A.1个 B.2个 C.3个 D.4个
5.如图,关于虚线成轴对称的有( )
A.1个 B.2个 C.3个 D.4个
6.等腰三角形是轴对称图形,等腰三角形有以下四类线:①底边上的高;②顶角的平分线;③底边的垂直平分线;④底边上的中线.其中是等腰三角形的对称轴的有 ( )
A.1个 B.2个 C.3个 D.4个
7.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定成立的是( )
A.AC=A′C′ B.AB∥B′C′ C.AA′⊥MN D.BO=B′O
8.【2020·哈尔滨】如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为( )
A.10° B.20° C.30° D.40°
第7题图 第8题图 第9题图
9.如图,△ABC和△ADE关于直线l对称,下列结论:①△ABC≌△ADE;②l垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上.其中错误的有 ( )
A.0个 B.1个 C.2个 D.3个
10.如图,△ABC和△A′B′C′关于直线l对称,AB与A′B′相交于l上的一点M,AC,A′C′相交于l上的一点N,若∠B=75°,∠C=85°,则下列关系式正确的是 ( )
A.∠1+∠2=180° B.∠1-∠2=40° C.∠1+∠2=80° D.∠1-∠2=20°
第10题图 第11题图 第13题图
11.如图,△ABC的面积为6,AC的长为3,△ABC′与△ABC关于直线AB对称,P是直线AC′上一动点,则线段BP的长不可能是 ( )
A.3 B.4 C.5 D.10
二、填空题
12.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的____________;轴对称图形的对称轴是任何一对对应点所连线段的____________.
13.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠ACD的度数是 .
14.如图,△ABC和△A′B′C′关于直线l对称.
(1)若∠A=30°,∠B′=40°,则∠C的度数为 ;
(2)若AC=5,BC=3,则A′B′的取值范围为 .
15.如图,l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=CD;③AB⊥BC;④AO=OC.其中正确的结论有 (把所有正确结论的序号都填在横线上).
16.如图,等边三角形ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 cm.
第14题图 第15题图 第16题图
三、解答题
17.如图的三组图形分别关于某条直线对称,请你使用无刻度的直尺分别画出它们的对称轴.
18.如图的阴影三角形与哪些三角形分别成轴对称?整个图形是轴对称图形吗?如果是,它共有几条对称轴?
19.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
20.【教学运算】如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4 cm,FC=1 cm,∠BAC=76°,∠EAC=58°.
(1)求BF的长度;
(2)求∠CAD的度数;
(3)连接EC,线段EC与直线MN有什么关系?并说明理由.
21.如图,已知△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)若直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹角α的数量关系.
22.如图,在直线MN上求作一点P,使∠MPA=∠NPB.(要求:写出作法)
23.如图,P是△ABC内一点,点D,E,F分别是点P关于直线AB,BC,CA的对称点,求∠ADB+∠BEC+∠CFA的度数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例1】如图,下列交通标志中,是轴对称图形的有( A )
A. 1个 B. 2个 C. 3个 D. 4个
解题秘方:根据轴对称图形的定义识别.
归纳:判断轴对称图形的方法
根据图形的特征,如果能找到一条直线,沿着这条直线折叠,直线两旁的部分能够互相重合,即可确定这个图形是轴对称图形,否则就不是轴对称图形.
【例2】如图的四组图形中,成轴对称的有( D )
A. 4组 B. 3组 C. 2组 D. 1组
解题秘方:根据轴对称的定义,沿着某条直线折叠,直线两旁的两个图形能完全重合,即成轴对称.
解:根据轴对称的定义,可以判断只有④中的两个图形沿着某一条直线折叠后,两个图形能够重合,所以成轴对称的只有1组.
方法归纳:反面观察法 从纸的反面观察图形,若观察到的和正面一样,就是成轴对称.
【例3】如图是轴对称图形,图中直线l是它的对称轴.请据此解决下列问题.
解题秘方:紧扣轴对称图形的性质进行说明.
(1)∠3和∠4有什么关系? AB与A′B′呢?
解:∠3=∠4, AB=A′B′.
(2)DD′与直线l有什么关系?
直线l是DD′的垂直平分线.
(3)写出图中其他相等关系.(不少于三对)
AD=A′D′,∠1=∠2,DC=D′C′.(答案不唯一)
【例4】如图,∠A=30°,∠C′=60°,△ABC与△A′B′C′关于直线l对称,则∠B=________.
解题秘方:紧扣成轴对称的性质确定对应元素进行计算.
解:∵△ ABC与△A′B′C′关于直线l对称,∠C′=60°,
∴∠C=∠C′=60°,
在△ABC中,
∠B=180°-∠A-∠C=180°-30°-60°=90°.
【同步练习】
一、选择题
1.【2021·鄂州】“国士无双”是人民对“杂交水稻之父”袁隆平院士的赞誉.下列四个汉字中是轴对称图形的是( B )
2.下列四种垃圾分类回收标志中,是轴对称图形的是 ( D )
3.【2021·枣庄】将如图的七巧板的其中几块,拼成一个多边形,为轴对称图形的是( D )
4.下列图形中的五边形ABCDE都是正五边形,则这些图形中的轴对称图形有 ( D )
A.1个 B.2个 C.3个 D.4个
5.如图,关于虚线成轴对称的有( C )
A.1个 B.2个 C.3个 D.4个
6.等腰三角形是轴对称图形,等腰三角形有以下四类线:①底边上的高;②顶角的平分线;③底边的垂直平分线;④底边上的中线.其中是等腰三角形的对称轴的有 ( A )
A.1个 B.2个 C.3个 D.4个
7.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列结论不一定成立的是( B )
A.AC=A′C′ B.AB∥B′C′ C.AA′⊥MN D.BO=B′O
8.【2020·哈尔滨】如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为( A )
A.10° B.20° C.30° D.40°
第7题图 第8题图 第9题图
9.如图,△ABC和△ADE关于直线l对称,下列结论:①△ABC≌△ADE;②l垂直平分DB;③∠C=∠E;④BC与DE的延长线的交点一定落在直线l上.其中错误的有 ( A )
A.0个 B.1个 C.2个 D.3个
10.如图,△ABC和△A′B′C′关于直线l对称,AB与A′B′相交于l上的一点M,AC,A′C′相交于l上的一点N,若∠B=75°,∠C=85°,则下列关系式正确的是 ( B )
A.∠1+∠2=180° B.∠1-∠2=40° C.∠1+∠2=80° D.∠1-∠2=20°
第10题图 第11题图 第13题图
11.如图,△ABC的面积为6,AC的长为3,△ABC′与△ABC关于直线AB对称,P是直线AC′上一动点,则线段BP的长不可能是 ( A )
A.3 B.4 C.5 D.10
二、填空题
12.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的____________;轴对称图形的对称轴是任何一对对应点所连线段的____________.
【答案】垂直平分线 垂直平分线
13.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠ACD的度数是 .
【答案】65°
14.如图,△ABC和△A′B′C′关于直线l对称.
(1)若∠A=30°,∠B′=40°,则∠C的度数为 ;
(2)若AC=5,BC=3,则A′B′的取值范围为 .
【答案】110° 2<A′B′<8
15.如图,l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=CD;③AB⊥BC;④AO=OC.其中正确的结论有 (把所有正确结论的序号都填在横线上).
【答案】①②④
16.如图,等边三角形ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 cm.
【答案】3
第14题图 第15题图 第16题图
三、解答题
17.如图的三组图形分别关于某条直线对称,请你使用无刻度的直尺分别画出它们的对称轴.
解:如图.
18.如图的阴影三角形与哪些三角形分别成轴对称?整个图形是轴对称图形吗?如果是,它共有几条对称轴?
解:题图中的阴影三角形与三角形2,3,4分别成轴对称.整个图形是轴对称图形.它共有4条对称轴.
19.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在G处,EF为折痕.
(1)求证:△FGC≌△EBC;
证明:由题意知
∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,
∴∠GCF=∠BCE.
∵∠G=∠D=∠B=90°,GC=AD=BC,
∴△FGC≌△EBC(ASA).
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
解:∵△FGC≌△EBC,∴GF=BE.
∵DF=GF,∴DF=BE.
∴四边形ECGF的面积=四边形AEFD的面积
=====16.
20.【教学运算】如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4 cm,FC=1 cm,∠BAC=76°,∠EAC=58°.
(1)求BF的长度;
解:∵△ABC与△ADE关于直线MN对称,ED=4 cm,
∴BC=ED=4 cm.
∵FC=1 cm,
∴BF=BC-FC=4-1=3(cm).
(2)求∠CAD的度数;
解:∵△ABC与△ADE关于直线MN对称,
∠BAC=76°,∴∠EAD=∠BAC=76°.
∵∠EAC=58°,
∴∠CAD=∠EAD-∠EAC=76°-58°=18°.
(3)连接EC,线段EC与直线MN有什么关系?并说明理由.
解:直线MN垂直平分线段EC.理由如下:
∵E,C关于直线MN对称,
∴直线MN垂直平分线段EC.
21.如图,已知△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
解:如图,连接B′B″,
画线段B′B″的垂直平分线EF,
则直线EF是△A′B′C′和△A″B″C″的对称轴.
(2)若直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹角α的数量关系.
解:如图,连接B′O.
∵△ABC和△A′B′C′关于直线MN对称,
∴∠BOM=∠B′OM.
∵△A′B′C′和△A″B″C″关于直线EF对称,
∴∠B′OE=∠B″OE.
∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE
=2(∠B′OM+∠B′OE)=2∠MOE,即∠BOB″=2α.
22.如图,在直线MN上求作一点P,使∠MPA=∠NPB.(要求:写出作法)
【思路点拨】在直线MN上求作一点P,使∠MPA=∠NPB,其实质是利用轴对称的性质在直线上找一点P使它到点A,B的距离之和最小.
解:①作点A关于直线MN的对称点A′;②连接BA′交直线MN于点P,连接AP,则∠MPA=∠NPB.
如图所示.
23.如图,P是△ABC内一点,点D,E,F分别是点P关于直线AB,BC,CA的对称点,求∠ADB+∠BEC+∠CFA的度数.
解:连接PA,PC.
∵点P,D关于直线AB对称,
∴AP=AD,BP=BD.
在△APB和△ADB中,
∴△APB≌△ADB(SSS).∴∠APB=∠ADB.
同理可证:∠BPC=∠BEC,∠APC=∠AFC.
∴∠ADB+∠BEC+∠CFA
=∠APB+∠BPC+∠APC
=360°.
