13.1.2.2 线段的垂直平分线的有关作图同步讲练(含答案)
文档属性
| 名称 | 13.1.2.2 线段的垂直平分线的有关作图同步讲练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 13:18:47 | ||
图片预览




文档简介
13.1 轴对称
13.1.2 线段的垂直平分线的性质
第2课时 线段的垂直平分线的有关作图
【知识重点】
知识点 画对称轴
1. 画对称轴的依据 画对称轴的依据是成轴对称和轴对称图形的性质,即对称轴就是任何一对对应点所连线段的垂直平分线.
2. 画对称轴的步骤
(1)找:找到任意一对对应点. (2)连:连接这对对应点.
(3)画:画出对应点所连线段的垂直平分线.这条垂直平分线就是对称轴.
特别解读
画轴对称图形的对称轴时,由于对称轴不一定只有一条,所以要注意选取不同的对应点,作出其所有的对称轴.
【经典例题】
【例】画出如图的图形的对称轴.
解题秘方:根据对称轴是轴对称图形中任意一对对应点所连线段的垂直平分线作对称轴.
【同步练习】
一、选择题
1.下列说法中,错误的是( )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个四边形对称
D.轴对称指的是两个图形沿着某一条直线对折后能完全重合
2.下列图形中,对称轴最多的是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
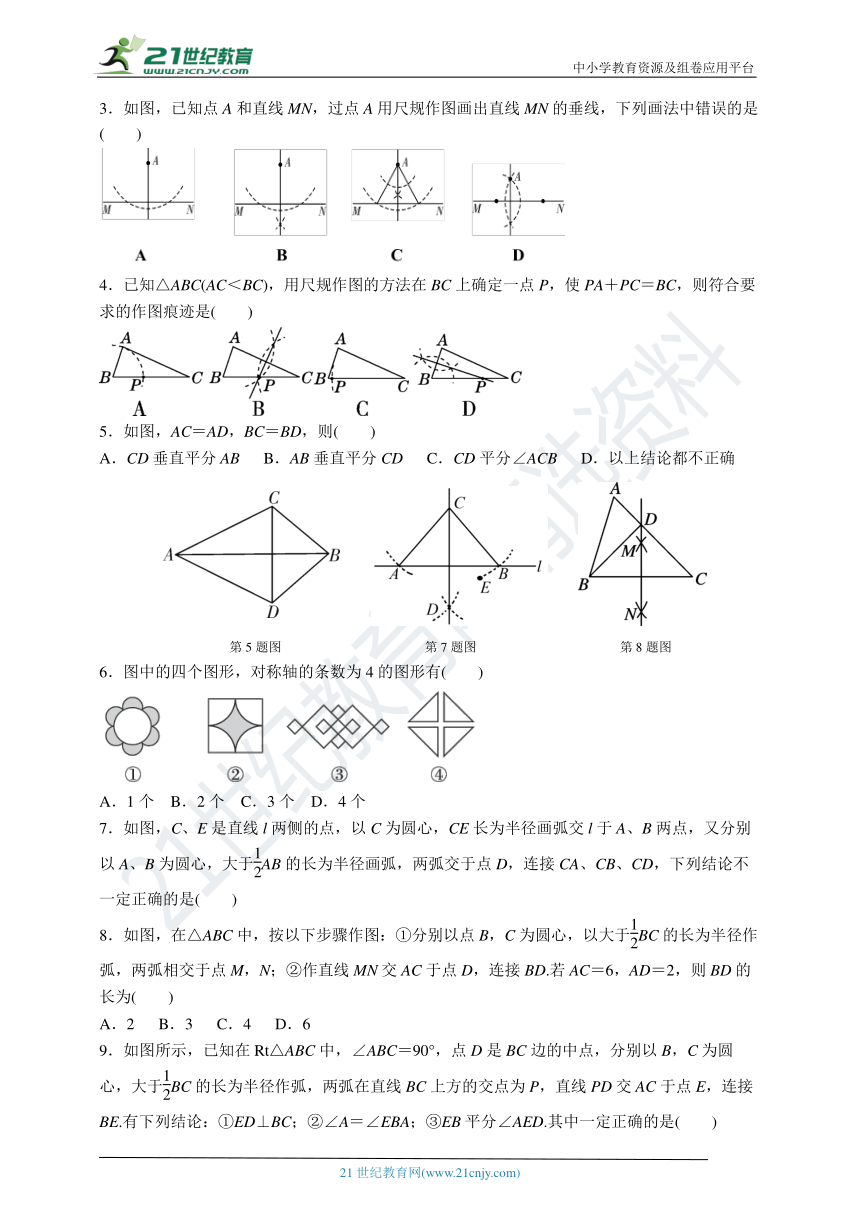
3.如图,已知点A和直线MN,过点A用尺规作图画出直线MN的垂线,下列画法中错误的是( )
4.已知△ABC(AC<BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )
5.如图,AC=AD,BC=BD,则( )
A.CD垂直平分AB B.AB垂直平分CD C.CD平分∠ACB D.以上结论都不正确
第5题图 第7题图 第8题图
6.图中的四个图形,对称轴的条数为4的图形有( )
A.1个 B.2个 C.3个 D.4个
7.如图,C、E是直线l两侧的点,以C为圆心,CE长为半径画弧交l于A、B两点,又分别以A、B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA、CB、CD,下列结论不一定正确的是( )
8.如图,在△ABC中,按以下步骤作图:①分别以点B,C为圆心,以大于BC的长为半径作弧,两弧相交于点M,N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( )
A.2 B.3 C.4 D.6
9.如图所示,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B,C为圆心,大于BC的长为半径作弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE.有下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED.其中一定正确的是( )
A.①②③ B.①② C.①③ D.②③
第9题图 第10题图 第13题图
10.如图,已知△ABC中,AC<BC,分别以点A,B为圆心,大于AB长为半径作弧,两弧交于点D,E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )
A.PA+PC=BC B.PA=PB C.DE⊥AB D.PA=PC
二、填空题
11.作线段AB的垂直平分线的方法:
(1)分别以__________为圆心,____________为半径作弧,两弧相交于C,D两点;
(2)作__________,即CD就是所求作的直线.
12.画对称轴就是作对称点所连线段的___________.
13.如图,在△ABC中,AB=6cm,AC=4cm,BC的垂直平分线分别交AB,BC于D,E,则△ACD的周长为 cm.
三、解答题
14.如图,在某河道l的同侧有两个村庄A,B,想要在河道上建一个水泵站,这个水泵站建在什么位置,能使两个村庄到水泵站的距离相等?
15.如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置 在图上标出它的位置.
16.请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,BC=CD,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.
17.如图,在△ABC中,点P是AC上一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等(不写作法,保留作图痕迹).
18.试找出如图所示的每个正多边形对称轴的条数,并填入表格中.
正多边形的边数 3 4 5 6 7 8
对称轴的条数
根据上表,请就一个正n边形对称轴的条数提出一个猜想:_________________________.
19.如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例】画出如图的图形的对称轴.
解题秘方:根据对称轴是轴对称图形中任意一对对应点所连线段的垂直平分线作对称轴.
解:作法:如图.
(1)连接BE;
(2)作线段BE的垂直平分线l,则直线l即为所求作的对称轴.
方法点拨:作轴对称图形的对称轴的两种方法
一是折叠法,将轴对称图形对折,折痕所在的直线为对称轴;二是先找到轴对称图形的一对对应点,再作连接这对对应点的线段的垂直平分线.
【同步练习】
一、选择题
1.下列说法中,错误的是( C )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个四边形对称
D.轴对称指的是两个图形沿着某一条直线对折后能完全重合
2.下列图形中,对称轴最多的是( B )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
3.如图,已知点A和直线MN,过点A用尺规作图画出直线MN的垂线,下列画法中错误的是( A )
4.已知△ABC(AC<BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( D )
5.如图,AC=AD,BC=BD,则( B )
A.CD垂直平分AB B.AB垂直平分CD C.CD平分∠ACB D.以上结论都不正确
第5题图 第7题图 第8题图
6.图中的四个图形,对称轴的条数为4的图形有( B )
A.1个 B.2个 C.3个 D.4个
7.如图,C、E是直线l两侧的点,以C为圆心,CE长为半径画弧交l于A、B两点,又分别以A、B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA、CB、CD,下列结论不一定正确的是( C )
8.如图,在△ABC中,按以下步骤作图:①分别以点B,C为圆心,以大于BC的长为半径作弧,两弧相交于点M,N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( C )
A.2 B.3 C.4 D.6
9.如图所示,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B,C为圆心,大于BC的长为半径作弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE.有下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED.其中一定正确的是( B )
A.①②③ B.①② C.①③ D.②③
第9题图 第10题图 第13题图
10.如图,已知△ABC中,AC<BC,分别以点A,B为圆心,大于AB长为半径作弧,两弧交于点D,E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( D )
A.PA+PC=BC B.PA=PB C.DE⊥AB D.PA=PC
二、填空题
11.作线段AB的垂直平分线的方法:
(1)分别以__________为圆心,____________为半径作弧,两弧相交于C,D两点;
(2)作__________,即CD就是所求作的直线.
【答案】点A和点B 大于AB的长 直线CD
12.画对称轴就是作对称点所连线段的___________.
【答案】垂直平分线
13.如图,在△ABC中,AB=6cm,AC=4cm,BC的垂直平分线分别交AB,BC于D,E,则△ACD的周长为 cm.
【答案】10
三、解答题
14.如图,在某河道l的同侧有两个村庄A,B,想要在河道上建一个水泵站,这个水泵站建在什么位置,能使两个村庄到水泵站的距离相等?
解:作线段AB的垂直平分线交l于点P,P即为水泵站的位置,作图略.
15.如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置 在图上标出它的位置.
解:如图,发射塔应修建在点P的位置.
16.请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,BC=CD,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.
【方法归纳】作轴对称图形的对称轴的两种方法.
一是折叠法,将轴对称图形对折,折痕所在的直线为对称轴;二是先找到轴对称图形的一对对应点,再作连接这对对应点的线段的垂直平分线.
解:(1)如图①,直线m即为所求.
(2)如图②,直线n即为所求.
17.如图,在△ABC中,点P是AC上一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等(不写作法,保留作图痕迹).
解:如图,点M即为所求.
18.试找出如图所示的每个正多边形对称轴的条数,并填入表格中.
正多边形的边数 3 4 5 6 7 8
对称轴的条数
【答案】3 4 5 6 7 8
根据上表,请就一个正n边形对称轴的条数提出一个猜想:_________________________.
【答案】正n边形有n条对称轴
19.如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
解:(1)如图所示; (2)∵△ABC和△A′B′C′关于直线MN对称,∴∠BOM=∠B′OM.又∵△A′B′C′和△A″B″C″关于直线EF对称,∴∠B′OE=∠B″OE.∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=2(∠B′OM+∠B′OE)=2α,即∠BOB″=2α.
13.1.2 线段的垂直平分线的性质
第2课时 线段的垂直平分线的有关作图
【知识重点】
知识点 画对称轴
1. 画对称轴的依据 画对称轴的依据是成轴对称和轴对称图形的性质,即对称轴就是任何一对对应点所连线段的垂直平分线.
2. 画对称轴的步骤
(1)找:找到任意一对对应点. (2)连:连接这对对应点.
(3)画:画出对应点所连线段的垂直平分线.这条垂直平分线就是对称轴.
特别解读
画轴对称图形的对称轴时,由于对称轴不一定只有一条,所以要注意选取不同的对应点,作出其所有的对称轴.
【经典例题】
【例】画出如图的图形的对称轴.
解题秘方:根据对称轴是轴对称图形中任意一对对应点所连线段的垂直平分线作对称轴.
【同步练习】
一、选择题
1.下列说法中,错误的是( )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个四边形对称
D.轴对称指的是两个图形沿着某一条直线对折后能完全重合
2.下列图形中,对称轴最多的是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
3.如图,已知点A和直线MN,过点A用尺规作图画出直线MN的垂线,下列画法中错误的是( )
4.已知△ABC(AC<BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )
5.如图,AC=AD,BC=BD,则( )
A.CD垂直平分AB B.AB垂直平分CD C.CD平分∠ACB D.以上结论都不正确
第5题图 第7题图 第8题图
6.图中的四个图形,对称轴的条数为4的图形有( )
A.1个 B.2个 C.3个 D.4个
7.如图,C、E是直线l两侧的点,以C为圆心,CE长为半径画弧交l于A、B两点,又分别以A、B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA、CB、CD,下列结论不一定正确的是( )
8.如图,在△ABC中,按以下步骤作图:①分别以点B,C为圆心,以大于BC的长为半径作弧,两弧相交于点M,N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( )
A.2 B.3 C.4 D.6
9.如图所示,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B,C为圆心,大于BC的长为半径作弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE.有下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED.其中一定正确的是( )
A.①②③ B.①② C.①③ D.②③
第9题图 第10题图 第13题图
10.如图,已知△ABC中,AC<BC,分别以点A,B为圆心,大于AB长为半径作弧,两弧交于点D,E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )
A.PA+PC=BC B.PA=PB C.DE⊥AB D.PA=PC
二、填空题
11.作线段AB的垂直平分线的方法:
(1)分别以__________为圆心,____________为半径作弧,两弧相交于C,D两点;
(2)作__________,即CD就是所求作的直线.
12.画对称轴就是作对称点所连线段的___________.
13.如图,在△ABC中,AB=6cm,AC=4cm,BC的垂直平分线分别交AB,BC于D,E,则△ACD的周长为 cm.
三、解答题
14.如图,在某河道l的同侧有两个村庄A,B,想要在河道上建一个水泵站,这个水泵站建在什么位置,能使两个村庄到水泵站的距离相等?
15.如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置 在图上标出它的位置.
16.请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,BC=CD,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.
17.如图,在△ABC中,点P是AC上一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等(不写作法,保留作图痕迹).
18.试找出如图所示的每个正多边形对称轴的条数,并填入表格中.
正多边形的边数 3 4 5 6 7 8
对称轴的条数
根据上表,请就一个正n边形对称轴的条数提出一个猜想:_________________________.
19.如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【经典例题】
【例】画出如图的图形的对称轴.
解题秘方:根据对称轴是轴对称图形中任意一对对应点所连线段的垂直平分线作对称轴.
解:作法:如图.
(1)连接BE;
(2)作线段BE的垂直平分线l,则直线l即为所求作的对称轴.
方法点拨:作轴对称图形的对称轴的两种方法
一是折叠法,将轴对称图形对折,折痕所在的直线为对称轴;二是先找到轴对称图形的一对对应点,再作连接这对对应点的线段的垂直平分线.
【同步练习】
一、选择题
1.下列说法中,错误的是( C )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个四边形对称
D.轴对称指的是两个图形沿着某一条直线对折后能完全重合
2.下列图形中,对称轴最多的是( B )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
3.如图,已知点A和直线MN,过点A用尺规作图画出直线MN的垂线,下列画法中错误的是( A )
4.已知△ABC(AC<BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( D )
5.如图,AC=AD,BC=BD,则( B )
A.CD垂直平分AB B.AB垂直平分CD C.CD平分∠ACB D.以上结论都不正确
第5题图 第7题图 第8题图
6.图中的四个图形,对称轴的条数为4的图形有( B )
A.1个 B.2个 C.3个 D.4个
7.如图,C、E是直线l两侧的点,以C为圆心,CE长为半径画弧交l于A、B两点,又分别以A、B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA、CB、CD,下列结论不一定正确的是( C )
8.如图,在△ABC中,按以下步骤作图:①分别以点B,C为圆心,以大于BC的长为半径作弧,两弧相交于点M,N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( C )
A.2 B.3 C.4 D.6
9.如图所示,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B,C为圆心,大于BC的长为半径作弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE.有下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED.其中一定正确的是( B )
A.①②③ B.①② C.①③ D.②③
第9题图 第10题图 第13题图
10.如图,已知△ABC中,AC<BC,分别以点A,B为圆心,大于AB长为半径作弧,两弧交于点D,E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( D )
A.PA+PC=BC B.PA=PB C.DE⊥AB D.PA=PC
二、填空题
11.作线段AB的垂直平分线的方法:
(1)分别以__________为圆心,____________为半径作弧,两弧相交于C,D两点;
(2)作__________,即CD就是所求作的直线.
【答案】点A和点B 大于AB的长 直线CD
12.画对称轴就是作对称点所连线段的___________.
【答案】垂直平分线
13.如图,在△ABC中,AB=6cm,AC=4cm,BC的垂直平分线分别交AB,BC于D,E,则△ACD的周长为 cm.
【答案】10
三、解答题
14.如图,在某河道l的同侧有两个村庄A,B,想要在河道上建一个水泵站,这个水泵站建在什么位置,能使两个村庄到水泵站的距离相等?
解:作线段AB的垂直平分线交l于点P,P即为水泵站的位置,作图略.
15.如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置 在图上标出它的位置.
解:如图,发射塔应修建在点P的位置.
16.请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,BC=CD,画出四边形ABCD的对称轴m;
(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.
【方法归纳】作轴对称图形的对称轴的两种方法.
一是折叠法,将轴对称图形对折,折痕所在的直线为对称轴;二是先找到轴对称图形的一对对应点,再作连接这对对应点的线段的垂直平分线.
解:(1)如图①,直线m即为所求.
(2)如图②,直线n即为所求.
17.如图,在△ABC中,点P是AC上一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等(不写作法,保留作图痕迹).
解:如图,点M即为所求.
18.试找出如图所示的每个正多边形对称轴的条数,并填入表格中.
正多边形的边数 3 4 5 6 7 8
对称轴的条数
【答案】3 4 5 6 7 8
根据上表,请就一个正n边形对称轴的条数提出一个猜想:_________________________.
【答案】正n边形有n条对称轴
19.如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
解:(1)如图所示; (2)∵△ABC和△A′B′C′关于直线MN对称,∴∠BOM=∠B′OM.又∵△A′B′C′和△A″B″C″关于直线EF对称,∴∠B′OE=∠B″OE.∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=2(∠B′OM+∠B′OE)=2α,即∠BOB″=2α.
