12.2.3 用“ASA”“AAS”判定三角形全等(共23张PPT)
文档属性
| 名称 | 12.2.3 用“ASA”“AAS”判定三角形全等(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 771.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-03 10:40:28 | ||
图片预览





文档简介
(共23张PPT)
第十二章 全等三角形
12.2.3用“ASA”“AAS”判定三角形全等
目录页
讲授新课
当堂练习
课堂小结
新课导入
学习目标
1.掌握三角形全等的“角边角”“角角边”条件.(重点)
2.能运用全等三角形的条件,解决简单的推理证明问题.(难点)
新课导入
【复习】(1)三角形中已知三个元素,包括哪几种情况?
三个角、三个边、两边一角、两角一边.
(2)到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?
三种:①定义;②SSS;③SAS.
【思考】 在三角形中,已知三个元素的四种情况中,我们研究了三种,
今天我们接着探究已知两角一边是否可以判断两三角形全等呢?
新课导入
【问题】 三角形中已知两角一边有几种可能?
1.两角和它们的夹边.
2.两角和其中一角的对边.
【作图验证】(用直尺和圆规)
先任意画出一个△ABC,再画一个△A′B′C′,使AB=A′B′、∠A=∠A′、∠B=∠B′(即两角和它们的夹边分别相等).把画出的△A′B′C′剪下来,放在△ABC上,它们能完全重合吗?(即全等吗)
A
C
B
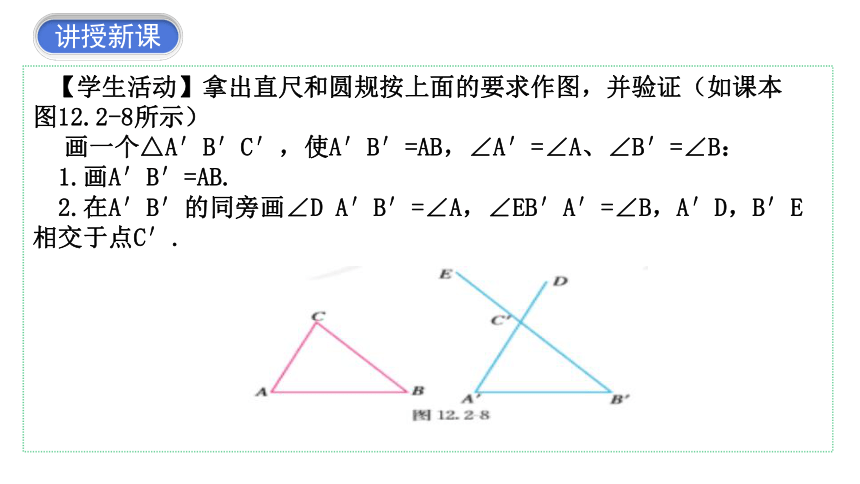
【学生活动】拿出直尺和圆规按上面的要求作图,并验证(如课本 图12.2-8所示)
画一个△A′B′C′,使A′B′=AB,∠A′=∠A、∠B′=∠B:
1.画A′B′=AB.
2.在A′B′的同旁画∠D A′B′=∠A,∠EB′A′=∠B,A′D,B′E相交于点C′.
讲授新课
【学生活动】在思考、实践的基础上可以归纳出下面判定两个三角形全等的定理.
(1)判定方法:两角和它们的夹边分别相等的两三角形全等(可以简写成“角边角”或“ASA”).
(2)判断两个三角形全等的推理过程,叫做证明三角形全等.
讲授新课
【思考】 在一个三角形中两角确定,第三个角一定确定.我们是不是可以不作图,用“ASA”推出“两角和其中一角的对边对应相等的两三角形全等”呢?
【探究问题】
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
讲授新课
讲授新课
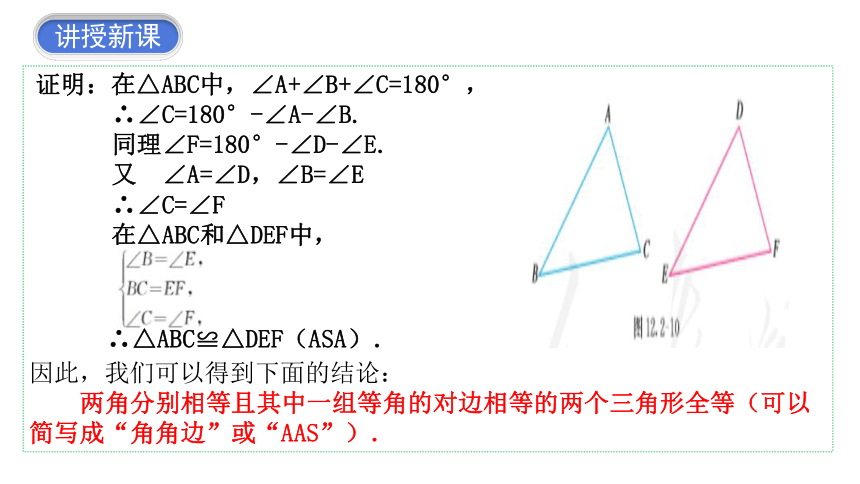
证明:在△ABC中,∠A+∠B+∠C=180°,
∴∠C=180°-∠A-∠B.
同理∠F=180°-∠D-∠E.
又 ∠A=∠D,∠B=∠E
∴∠C=∠F
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
因此,我们可以得到下面的结论:
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
讲授新课
已知:∠ABC=∠DCB,∠ACB= ∠DBC,求证:△ABC≌△DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
证明:
在△ABC和△DCB中,
∴△ABC≌△DCB(ASA ).
B
C
A
D
判定方法:两角和它们的夹边对应相等两个三角形全等.
例1
讲授新课
在证两三角形全等所需要的角相等时,目前通常采用的方法有:
(1)公共角、对顶角分别相等;
(2)等角加(减)等角,其和(差)相等,即等式的性质;
(3)同角或等角的余(补)角相等;
(4)角平分线得到相等角;
(5)平行线的同位角、内错角相等;
(6)直角都相等;
(7)全等三角形对应角相等;
(8)第三角代换,即等量代换等.
总结
2. 如图,AD⊥BC于点D,AD平分∠BAC.求证:△ABD ≌△ACD.
证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∴△ABD≌△ACD(ASA).
在△ABD和△ACD中,
例2
讲授新课
判定两三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法看缺什么条件,再去证什么条件,简言之:即综合利用分析法和综合法寻找证明途径.
利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
方法总结
1、全等三角形的判定(3):
_________________分别相等的两个三角形全等(ASA).
几何语言:
如图,在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
两角和它们的夹边
BC=EF
∠C=∠F
当堂练习
2、全等三角形的判定(4):
__________________相等的两个三角形全等(AAS).
几何语言:
如图,在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
两角及一角所对边
∠A=∠D
BC=EF
当堂练习
3. 如图,AB和CD相交于点O,∠A=∠C,OA=OC.求证:△AOD ≌△COB.
∴△AOD≌△COB(ASA).
证明:在△AOD和△COB中,
当堂练习
4、如图,∠BAC=∠DAE=90°,∠B=∠C,AD=AE.求证:△ABD ≌△ACE.
证明:∵∠BAC=∠DAE=90°,
∴∠BAC-∠CAD=∠DAE-∠CAD.
即∠BAD=∠CAE.
∴△ABD≌△ACE(AAS).
在△ABD和△ACE中,
当堂练习
5、如图,B是AC的中点,BD∥CE,AD∥BE. 求证:BD=CE.
证明:∵BD∥CE,
∴∠ABD=∠BCE.
∵AD∥BE,∴∠A=∠CBE.
又AB=BC,
∴△ABD≌△BCE(ASA).
∴BD=CE.
当堂练习
当堂练习
6、如图,E,F 在线段AC上,AD∥CB,AE = CF.若∠B =∠D,求证:DF =BE.
A
B
C
D
E
F
证明:∵AD∥CB ,
∴∠A =∠C.
∵AE =CF ,
∴AF =CE.
在△ADF 和△CBE 中,
∠A =∠C,
∠D =∠B ,
AF =CE ,
∴△ADF ≌△CBE(AAS).
∴DF =BE.
当堂练习
7、如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE. 求证:△ABC与△DEC全等.
证明: ∵∠BCE=∠ACD=90°,
∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,
∴∠1=∠D,
在△ABC和△DEC中,
∴△ABC≌△DEC(AAS).
课堂小结
边角边
角角边
内 容
有两角及夹边对应相等的两个三角形全等(简写成 “ASA”)
应用
为证明线段和角相等提供了新的证法
注意
注意“角角边”、“角边角”中两角与边的区别
【必做作业】
课时分层作业本第14页的A组与B组.
【选做作业】
课时分层作业本第14页的C组.
作业布置
THANKS!
第十二章 全等三角形
12.2.3用“ASA”“AAS”判定三角形全等
目录页
讲授新课
当堂练习
课堂小结
新课导入
学习目标
1.掌握三角形全等的“角边角”“角角边”条件.(重点)
2.能运用全等三角形的条件,解决简单的推理证明问题.(难点)
新课导入
【复习】(1)三角形中已知三个元素,包括哪几种情况?
三个角、三个边、两边一角、两角一边.
(2)到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?
三种:①定义;②SSS;③SAS.
【思考】 在三角形中,已知三个元素的四种情况中,我们研究了三种,
今天我们接着探究已知两角一边是否可以判断两三角形全等呢?
新课导入
【问题】 三角形中已知两角一边有几种可能?
1.两角和它们的夹边.
2.两角和其中一角的对边.
【作图验证】(用直尺和圆规)
先任意画出一个△ABC,再画一个△A′B′C′,使AB=A′B′、∠A=∠A′、∠B=∠B′(即两角和它们的夹边分别相等).把画出的△A′B′C′剪下来,放在△ABC上,它们能完全重合吗?(即全等吗)
A
C
B
【学生活动】拿出直尺和圆规按上面的要求作图,并验证(如课本 图12.2-8所示)
画一个△A′B′C′,使A′B′=AB,∠A′=∠A、∠B′=∠B:
1.画A′B′=AB.
2.在A′B′的同旁画∠D A′B′=∠A,∠EB′A′=∠B,A′D,B′E相交于点C′.
讲授新课
【学生活动】在思考、实践的基础上可以归纳出下面判定两个三角形全等的定理.
(1)判定方法:两角和它们的夹边分别相等的两三角形全等(可以简写成“角边角”或“ASA”).
(2)判断两个三角形全等的推理过程,叫做证明三角形全等.
讲授新课
【思考】 在一个三角形中两角确定,第三个角一定确定.我们是不是可以不作图,用“ASA”推出“两角和其中一角的对边对应相等的两三角形全等”呢?
【探究问题】
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
讲授新课
讲授新课
证明:在△ABC中,∠A+∠B+∠C=180°,
∴∠C=180°-∠A-∠B.
同理∠F=180°-∠D-∠E.
又 ∠A=∠D,∠B=∠E
∴∠C=∠F
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
因此,我们可以得到下面的结论:
两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
讲授新课
已知:∠ABC=∠DCB,∠ACB= ∠DBC,求证:△ABC≌△DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
证明:
在△ABC和△DCB中,
∴△ABC≌△DCB(ASA ).
B
C
A
D
判定方法:两角和它们的夹边对应相等两个三角形全等.
例1
讲授新课
在证两三角形全等所需要的角相等时,目前通常采用的方法有:
(1)公共角、对顶角分别相等;
(2)等角加(减)等角,其和(差)相等,即等式的性质;
(3)同角或等角的余(补)角相等;
(4)角平分线得到相等角;
(5)平行线的同位角、内错角相等;
(6)直角都相等;
(7)全等三角形对应角相等;
(8)第三角代换,即等量代换等.
总结
2. 如图,AD⊥BC于点D,AD平分∠BAC.求证:△ABD ≌△ACD.
证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∴△ABD≌△ACD(ASA).
在△ABD和△ACD中,
例2
讲授新课
判定两三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法看缺什么条件,再去证什么条件,简言之:即综合利用分析法和综合法寻找证明途径.
利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
方法总结
1、全等三角形的判定(3):
_________________分别相等的两个三角形全等(ASA).
几何语言:
如图,在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
两角和它们的夹边
BC=EF
∠C=∠F
当堂练习
2、全等三角形的判定(4):
__________________相等的两个三角形全等(AAS).
几何语言:
如图,在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
两角及一角所对边
∠A=∠D
BC=EF
当堂练习
3. 如图,AB和CD相交于点O,∠A=∠C,OA=OC.求证:△AOD ≌△COB.
∴△AOD≌△COB(ASA).
证明:在△AOD和△COB中,
当堂练习
4、如图,∠BAC=∠DAE=90°,∠B=∠C,AD=AE.求证:△ABD ≌△ACE.
证明:∵∠BAC=∠DAE=90°,
∴∠BAC-∠CAD=∠DAE-∠CAD.
即∠BAD=∠CAE.
∴△ABD≌△ACE(AAS).
在△ABD和△ACE中,
当堂练习
5、如图,B是AC的中点,BD∥CE,AD∥BE. 求证:BD=CE.
证明:∵BD∥CE,
∴∠ABD=∠BCE.
∵AD∥BE,∴∠A=∠CBE.
又AB=BC,
∴△ABD≌△BCE(ASA).
∴BD=CE.
当堂练习
当堂练习
6、如图,E,F 在线段AC上,AD∥CB,AE = CF.若∠B =∠D,求证:DF =BE.
A
B
C
D
E
F
证明:∵AD∥CB ,
∴∠A =∠C.
∵AE =CF ,
∴AF =CE.
在△ADF 和△CBE 中,
∠A =∠C,
∠D =∠B ,
AF =CE ,
∴△ADF ≌△CBE(AAS).
∴DF =BE.
当堂练习
7、如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE. 求证:△ABC与△DEC全等.
证明: ∵∠BCE=∠ACD=90°,
∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,
∴∠1=∠D,
在△ABC和△DEC中,
∴△ABC≌△DEC(AAS).
课堂小结
边角边
角角边
内 容
有两角及夹边对应相等的两个三角形全等(简写成 “ASA”)
应用
为证明线段和角相等提供了新的证法
注意
注意“角角边”、“角边角”中两角与边的区别
【必做作业】
课时分层作业本第14页的A组与B组.
【选做作业】
课时分层作业本第14页的C组.
作业布置
THANKS!
