2023-2024学年人教版(五四制)八年级数学上册 20.1—22.1 阶段性综合练习题(含解析)
文档属性
| 名称 | 2023-2024学年人教版(五四制)八年级数学上册 20.1—22.1 阶段性综合练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 304.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-03 00:00:00 | ||
图片预览




文档简介
2023-2024学年人教版(五四学制)八年级数学上册《20.1—22.1》
阶段性综合练习题
一、选择题(共30分)
1.下列运算中,正确的是( )
A.a a2=a3 B.(ab2)2=a2b2 C.3a6÷a3=3a2 D.4a﹣3a=1
2.下列图形不是轴对称图形的是( )
A. B. C. D.
3.下列四个式子:,x2+x,m,,其中分式的个数有( )
A.1个 B.2个 C.3个 D.4个
4.点M(1,2)关于x轴对称点的坐标为( )
A.(﹣1,2) B.(﹣1,﹣2) C.(2,﹣1) D.(1,﹣2)
5.在Rt△ABC中,∠C=90°,∠B=30°,AB=8cm,则AC的长为( )
A.2cm B.3cm C.4cm D.5cm
6.下列多项式中,能用平方差公式因式分解的是( )
A.a2+(﹣b)2 B.﹣x2﹣y2 C.﹣m2+9 D.3x2y﹣27xy2
7.计算(﹣2)2022×()2022的值是( )
A.﹣1 B.1 C. D.2
8.直接依据图中图形面积之间的关系,通过计算可以表示的等式是( )
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)2=a2+2ab+b2
C.2a(a+b)=2a2+2ab D.(a+b)(a﹣b)=a2﹣b2
9.如图,在△ABC中,AB=AC=8,∠ABC=30°,AD是△ABC的高,AE平分∠BAD,过点D作DF∥AB交AE的延长线于点F,则DF的长是( )
A.2 B.4 C.6 D.8
10.下列命题:①有一个外角等于120°的等腰三角形是等边三角形;②等腰三角形的一边长为4,另一边长为9,则这个等腰三角形的周长为17或22;③两个单项式的积仍是单项式;④形如的式子是分式;⑤三角形两边垂直平分线的交点到三角形三边的距离相等.其中正确的命题有( )个.
A.1个 B.2个 C.3个 D.4个
二、填空题(共18分)
11.当x 时,分式有意义.
12.分解因式:ma2﹣4mb2= .
13.计算:(12a3﹣6a2+3a)÷3a= .
14.在△ABC中,AB=AC,∠C=80°,则∠A= .
15.如果多项式x2+mx+9是一个完全平方式,则m的值是 .
16.如图,在△ABC中,点D为BC边的中点,过点D作DP⊥BC,连接CP并延长交边AB于点F,连接BP并延长交边AC于点E,∠A=∠CPE=60°,,则S△PBF+S△PCE的值为 .
三、解答题(满分72分)
17.因式分解:
(1)p(a2+b2)﹣q(a2+b2);
(2)(a+b)2﹣12(a+b)+36.
18.计算:
(1)(﹣a2)5 (b4)2÷(ab)3;
(2)982+98×4+4(用简便算法计算).
19.先化简,再求值:
x2(x﹣1)﹣x(x2+x﹣1),其中x=20220﹣.
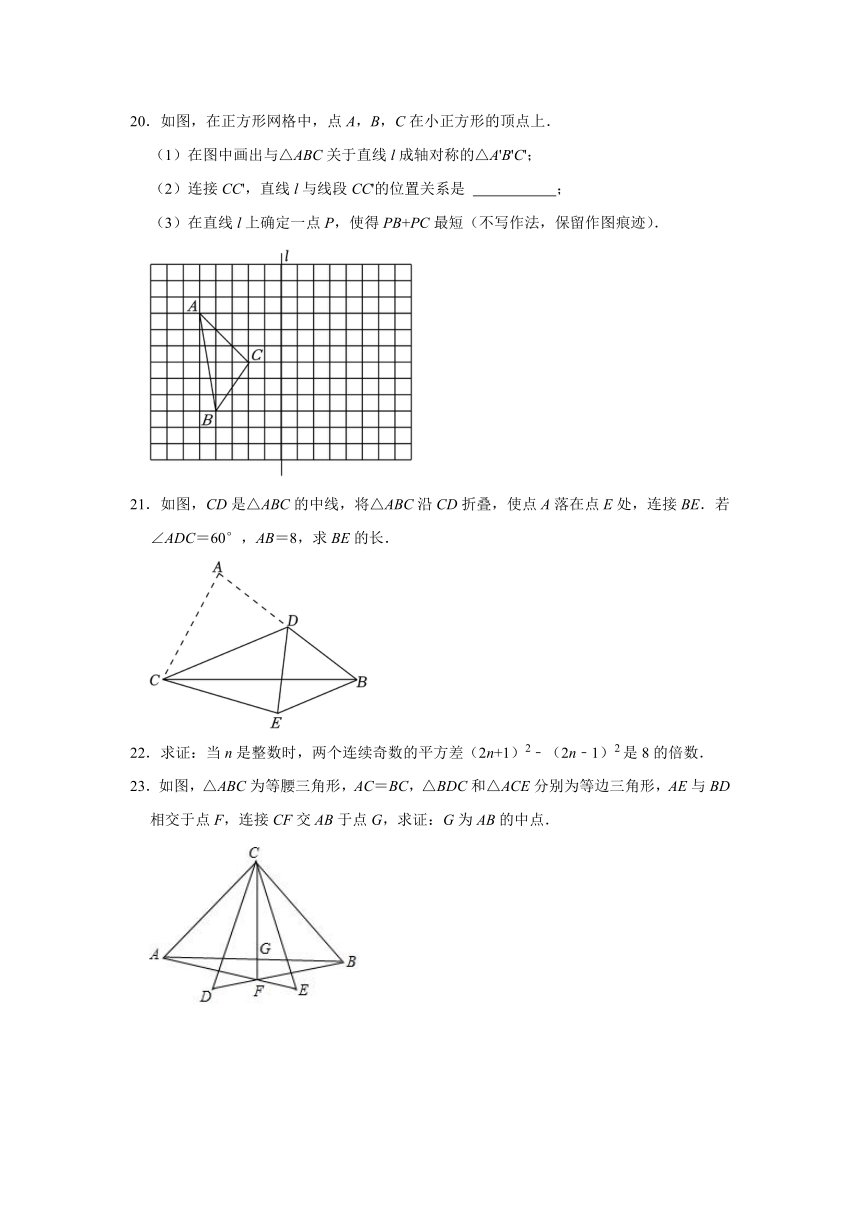
20.如图,在正方形网格中,点A,B,C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△A'B'C';
(2)连接CC',直线l与线段CC'的位置关系是 ;
(3)在直线l上确定一点P,使得PB+PC最短(不写作法,保留作图痕迹).
21.如图,CD是△ABC的中线,将△ABC沿CD折叠,使点A落在点E处,连接BE.若∠ADC=60°,AB=8,求BE的长.
22.求证:当n是整数时,两个连续奇数的平方差(2n+1)2﹣(2n﹣1)2是8的倍数.
23.如图,△ABC为等腰三角形,AC=BC,△BDC和△ACE分别为等边三角形,AE与BD相交于点F,连接CF交AB于点G,求证:G为AB的中点.
24.在学习《因式分解》时,邹老师给同学们发了很多硬纸片(a×a的正方形A,b×b的正方形B,a×b的长方形C).
(1)在探究中,小明用1张A和1张C组成如图1所示的长方形可以说明b2+ab可以分解为 ;
(2)继续探究中,小明用1张A,2张B和3张C再次拼得一个长方形,请在框1中画出示意图,并将长方形面积表达式的因式分解结果写在横线上;
(3)尝试应用:请你仿照小明同学的探究方法,尝试用1张A,4张B和若干张C拼成一个长方形或者正方形,请你设计两种不同的拼法,在框2和框3中分别画出示意图,并在相应的横线上写出所拼长方形的面积表达式及因式分解的结果.
25.如图1,等边△ABC中,点D在BC上,点E在AC上,连接AD,BE交于点F,CD=AE.
(1)求∠BFD的度数;
(2)如图2,连接CF,若CF⊥BE,求证:BF=2AF;
(3)如图3,在(2)的条件下,将AD沿CF翻折交AC于点G,过点C作CF的垂线交直线FG于点H,若BF=4,求GH的长.
参考答案
一、选择题(共30分)
1.解:A、原式=a3,符合题意;
B、原式=a2b4,不符合题意;
C、原式=3a3,不符合题意;
D、原式=a,不符合题意.
故选:A.
2.解:A、是轴对称图形,故选项错误;
B、不是轴对称图形,故选项正确;
C、是轴对称图形,故选项错误;
D、是轴对称图形,故选项错误.
故选:B.
3.解:分母上含有字母的式子是分式,题目中所给的式子中只有,两个分母中都含有字母,所以这两个是分式,
故选:B.
4.解:∵2的相反数是﹣2,
∴点M(1,2)关于x轴对称点的坐标为 (1,﹣2).
故选:D.
5.解:Rt△ABC中,∠C=90°,∠B=30°,AB=8cm,
AC=AB=×8=4(cm).
故选:C.
6.解:A:a2+(﹣b)2=a2+b2是两数的平方和,故A错;
B:﹣x2﹣y2=﹣(x2+y2)是两数平方和的相反数,故B错;
C:﹣m2+9=32﹣m2平方差,故C正确;
D:3x2y﹣27xy2=3xy(x﹣9y),没有平方差,故D错,
故选:C.
7.解:(﹣2)2022×()2022
=(﹣2×)2022
=(﹣1)2022
=1.
故选:B.
8.解:从整体上看是边长为a+b的正方形,因此面积为(a+b)2,
从各个部分看,整个图形由是边长为a的正方形,边长为b的正方形以及两个长为a、宽为b的长方形拼成,因此面积为a2+2ab+b2,
所以(a+b)2=a2+2ab+b2,
故选:B.
9.解:∵AD⊥BC,
∴∠ADB=90°,
AD=AB=4(根据直角三角形30度角的性质),
∵AE平分∠BAD,
∴∠BAF=∠DAF,
∵DF∥AB,
∴∠F=∠BAF,
∴∠F=∠DAF,
∴DF=AD=4.
故选:B.
10.解:有一个外角等于120°,即有一个内角等于60°,这样的等腰三角形是等边三角形,故①正确;
等腰三角形的一边长为4,另一边长为9,则第三边只能为9,这个等腰三角形的周长为22,故②错误;
两个单项式的积仍是单项式,故③正确;
形如的式子,当B中不含有字母时,不是分式,故④错误;
三角形两边垂直平分线的交点到三角形三个顶点的距离相等,故⑤错误;
∴正确的命题有①③,共2个,
故选:B.
二、填空题(共18分)
11.解:∵分式有意义的条件是分母不等于0,
∴x﹣1≠0,解得x≠1,
故答案为:x≠1.
12.解:ma2﹣4mb2
=m(a2﹣4b2)
=m(a+2b)(a﹣2b),
故答案为:m(a+2b)(a﹣2b).
13.解:原式=4a2﹣2a+1.
故答案为:4a2﹣2a+1.
14.解:∵AB=AC,
∴∠B=∠C=80°,
∴∠A=180°﹣∠B﹣∠C=20°,
故答案为:20°.
15.解:∵x2+mx+9
=x2+mx+(±3)2
=(x±3)2,
∴m=2×1×(±#)=±6,
故答案为:±6.
16.解:作BM⊥CF于点M,CN⊥BN于点N,
∴∠BMF=∠CNE=90°,
∵点D为BC边的中点,DP⊥BC,
∴PB=PC,
∴∠PBC=∠PCB,
∵BP=CP,∠BMP=∠CNP,且∠BPM=∠CPN,
∴△BPM≌△CPN(AAS),
∴BM=CN,PM=PN,S△BPM=S△CPN,
∵∠A=∠BPF=60°,
∴∠BFP=∠BEA,
∵∠BEA=∠CEN,
∴∠CEN=∠BFP,
在△BFM和△CEN中,
,
∴△BFM≌△CEN(AAS),
∴FM=NE,S△BFM=S△CEN,
∴S△PBF+S△PCE=2S△BPM,
∵∠BPF=60°,BP=CP,
∴∠PBD=∠PCD=30°,
∴∠MBP=∠PBD=30°,且BP=BP,∠BMP=∠BDP=90°,
∴△BMP≌△BDP(AAS),
∴,
∴,
故答案为:.
三、解答题(满分72分)
17.解:(1)p(a2+b2)﹣q(a2+b2)
=(a2+b2)(p﹣q);
(2)(a+b)2﹣12(a+b)+36
=(a+b﹣6)2.
18.解:(1)原式=﹣a10b8÷a3b3
=﹣a7b5;
(2)原式=982+2×98×2+22
=(98+2)2
=1002
=10000.
19.解:原式=x3﹣x2﹣x3﹣x2+x
=﹣2x2+x,
∵x=20220﹣=1﹣=,
∴原式=﹣2×()2+=0.
20.解:(1)如图所示,△A'B'C'即为所求;
(2)线段CC′被直线l垂直平分.
故答案为:垂直平分;
(3)连接BC′交直线l于点P,则点P即为所求点.
21.解:∵CD是△ABC的中线,AB=8,
∴AD=BD=AB=×8=4,
∵△ABC沿CD折叠,使点A落在点E处,
∴AD=DE,∠ADC=∠EDC=60°,
∴DE=DB,
∵∠BDE=180°﹣∠ADC﹣∠EDC=60°,
∴△EDB是等边三角形,
∴BE=BD=4.
22.解:∵(2n+1)2﹣(2n﹣1)2=[(2n+1)+(2n﹣1)][(2n+1)﹣(2n﹣1)]
=4n×2
=8n,
∴当n是整数时,两个连续奇数的平方差(2n+1)2﹣(2n﹣1)2是8的倍数.
23.证明:∵AC=BC,
∴∠CAB=∠CBA,
∵△AEC和△BCD为等边三角形,
∴∠CAE=∠CBD,∠FAG=∠FBG,
∴AF=BF.
在△AFC和△BFC中,
,
∴△AFC≌△BFC(SSS),
∴∠ACF=∠BCF,
即CF平分∠ACB,
又∵AC=BC,
∴AG=BG,
即G为AB的中点.
24.解:(1)b2+ab=b(b+a),
故答案为:b(b+a);
(2)a2+3ab+2b2=(a+b)(a+2b),
故答案为:(a+b)(a+2b);
(3)a2+4b2+4ab=(a+2b)2,
a2+4b2+5ab=(a+b)(a+4b),
25.(1)解:∵等边△ABC,
∴AB=CA,∠BAE=∠ACD=60°,
在△ACD与△BAE中,
,
∴△ACD≌△BAE(SAS),
∴∠DAC=∠EBA,
∵∠BFD=∠BAF+∠ABF,
∴∠BFD=∠BAF+∠CAD=∠BAC=60°.
(2)证明:在BF上截取BQ=AF,连接AQ,
在△QBA与△FAC中,
,
∴△QBA≌△FAC(SAS),
∴∠BAQ=∠ACF,
∴∠QBA+∠BAQ=∠DAC+∠BAQ=∠DAC+∠ACF,
∵∠AQF=∠QBA+∠BAQ,∠DFC=∠DAC+∠ACF,
∴∠AQF=∠DFC=∠BAQ+∠DAC.
∵CF⊥BE,∠BFD=60°,
∴∠AQF=∠DFC=∠BAQ+∠DAC=30°,
∴∠AQF=∠DFC=∠QAF=30°,
∴AF=FQ,
∴AF=FQ=BQ,
∵BF=FQ+BQ=2FQ,
∴BF=2AF.
(3)解:如图,延长BE到点N,使得AF=FN,连接AN,连接CN,交FH于点M,
∵∠BFD=∠AFN=60°,
∴△AFN是等边三角形,
∴AF=AN=FN,∠FAN=∠FNA=∠AFN=60°,
∴∠BAF=60°﹣∠FAE=∠CAN,
在△BAF与△CAN中,
,
∴△BAF≌△CAN(SAS),
∴BF=CN,∠ABF=∠ACN,
∵∠DAC=∠EBA,
∴∠DAC=∠ACN,
∴CN∥AD,
∴∠AFN=∠FNM=60°,
∵CF⊥BE,
∴∠FCN=30°,
∵∠DFC=30°,AD沿CF翻折交AC于点G,CF⊥CH,
∴∠DFC=∠MFC=∠MCF=30°,∠MFN=∠MCH=∠MHC=60°,
∴MF=MC,∠CMH=∠FMN=60°,
∴△MCF是等腰三角形,△CMH,△MFN是等边三角形,
∴AF=AN=CM=HM=MF=MN=FN,
∵BF=4,BF=2AF,
∴AF=2=AN=CM=HM=MF=MN=FN;
在△AGF与△CGM中,
,
∴△AGF≌△CGM(SAS),
∴,
∴GH=HM+MG=2+1=3.
阶段性综合练习题
一、选择题(共30分)
1.下列运算中,正确的是( )
A.a a2=a3 B.(ab2)2=a2b2 C.3a6÷a3=3a2 D.4a﹣3a=1
2.下列图形不是轴对称图形的是( )
A. B. C. D.
3.下列四个式子:,x2+x,m,,其中分式的个数有( )
A.1个 B.2个 C.3个 D.4个
4.点M(1,2)关于x轴对称点的坐标为( )
A.(﹣1,2) B.(﹣1,﹣2) C.(2,﹣1) D.(1,﹣2)
5.在Rt△ABC中,∠C=90°,∠B=30°,AB=8cm,则AC的长为( )
A.2cm B.3cm C.4cm D.5cm
6.下列多项式中,能用平方差公式因式分解的是( )
A.a2+(﹣b)2 B.﹣x2﹣y2 C.﹣m2+9 D.3x2y﹣27xy2
7.计算(﹣2)2022×()2022的值是( )
A.﹣1 B.1 C. D.2
8.直接依据图中图形面积之间的关系,通过计算可以表示的等式是( )
A.(a﹣b)2=a2﹣2ab+b2 B.(a+b)2=a2+2ab+b2
C.2a(a+b)=2a2+2ab D.(a+b)(a﹣b)=a2﹣b2
9.如图,在△ABC中,AB=AC=8,∠ABC=30°,AD是△ABC的高,AE平分∠BAD,过点D作DF∥AB交AE的延长线于点F,则DF的长是( )
A.2 B.4 C.6 D.8
10.下列命题:①有一个外角等于120°的等腰三角形是等边三角形;②等腰三角形的一边长为4,另一边长为9,则这个等腰三角形的周长为17或22;③两个单项式的积仍是单项式;④形如的式子是分式;⑤三角形两边垂直平分线的交点到三角形三边的距离相等.其中正确的命题有( )个.
A.1个 B.2个 C.3个 D.4个
二、填空题(共18分)
11.当x 时,分式有意义.
12.分解因式:ma2﹣4mb2= .
13.计算:(12a3﹣6a2+3a)÷3a= .
14.在△ABC中,AB=AC,∠C=80°,则∠A= .
15.如果多项式x2+mx+9是一个完全平方式,则m的值是 .
16.如图,在△ABC中,点D为BC边的中点,过点D作DP⊥BC,连接CP并延长交边AB于点F,连接BP并延长交边AC于点E,∠A=∠CPE=60°,,则S△PBF+S△PCE的值为 .
三、解答题(满分72分)
17.因式分解:
(1)p(a2+b2)﹣q(a2+b2);
(2)(a+b)2﹣12(a+b)+36.
18.计算:
(1)(﹣a2)5 (b4)2÷(ab)3;
(2)982+98×4+4(用简便算法计算).
19.先化简,再求值:
x2(x﹣1)﹣x(x2+x﹣1),其中x=20220﹣.
20.如图,在正方形网格中,点A,B,C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△A'B'C';
(2)连接CC',直线l与线段CC'的位置关系是 ;
(3)在直线l上确定一点P,使得PB+PC最短(不写作法,保留作图痕迹).
21.如图,CD是△ABC的中线,将△ABC沿CD折叠,使点A落在点E处,连接BE.若∠ADC=60°,AB=8,求BE的长.
22.求证:当n是整数时,两个连续奇数的平方差(2n+1)2﹣(2n﹣1)2是8的倍数.
23.如图,△ABC为等腰三角形,AC=BC,△BDC和△ACE分别为等边三角形,AE与BD相交于点F,连接CF交AB于点G,求证:G为AB的中点.
24.在学习《因式分解》时,邹老师给同学们发了很多硬纸片(a×a的正方形A,b×b的正方形B,a×b的长方形C).
(1)在探究中,小明用1张A和1张C组成如图1所示的长方形可以说明b2+ab可以分解为 ;
(2)继续探究中,小明用1张A,2张B和3张C再次拼得一个长方形,请在框1中画出示意图,并将长方形面积表达式的因式分解结果写在横线上;
(3)尝试应用:请你仿照小明同学的探究方法,尝试用1张A,4张B和若干张C拼成一个长方形或者正方形,请你设计两种不同的拼法,在框2和框3中分别画出示意图,并在相应的横线上写出所拼长方形的面积表达式及因式分解的结果.
25.如图1,等边△ABC中,点D在BC上,点E在AC上,连接AD,BE交于点F,CD=AE.
(1)求∠BFD的度数;
(2)如图2,连接CF,若CF⊥BE,求证:BF=2AF;
(3)如图3,在(2)的条件下,将AD沿CF翻折交AC于点G,过点C作CF的垂线交直线FG于点H,若BF=4,求GH的长.
参考答案
一、选择题(共30分)
1.解:A、原式=a3,符合题意;
B、原式=a2b4,不符合题意;
C、原式=3a3,不符合题意;
D、原式=a,不符合题意.
故选:A.
2.解:A、是轴对称图形,故选项错误;
B、不是轴对称图形,故选项正确;
C、是轴对称图形,故选项错误;
D、是轴对称图形,故选项错误.
故选:B.
3.解:分母上含有字母的式子是分式,题目中所给的式子中只有,两个分母中都含有字母,所以这两个是分式,
故选:B.
4.解:∵2的相反数是﹣2,
∴点M(1,2)关于x轴对称点的坐标为 (1,﹣2).
故选:D.
5.解:Rt△ABC中,∠C=90°,∠B=30°,AB=8cm,
AC=AB=×8=4(cm).
故选:C.
6.解:A:a2+(﹣b)2=a2+b2是两数的平方和,故A错;
B:﹣x2﹣y2=﹣(x2+y2)是两数平方和的相反数,故B错;
C:﹣m2+9=32﹣m2平方差,故C正确;
D:3x2y﹣27xy2=3xy(x﹣9y),没有平方差,故D错,
故选:C.
7.解:(﹣2)2022×()2022
=(﹣2×)2022
=(﹣1)2022
=1.
故选:B.
8.解:从整体上看是边长为a+b的正方形,因此面积为(a+b)2,
从各个部分看,整个图形由是边长为a的正方形,边长为b的正方形以及两个长为a、宽为b的长方形拼成,因此面积为a2+2ab+b2,
所以(a+b)2=a2+2ab+b2,
故选:B.
9.解:∵AD⊥BC,
∴∠ADB=90°,
AD=AB=4(根据直角三角形30度角的性质),
∵AE平分∠BAD,
∴∠BAF=∠DAF,
∵DF∥AB,
∴∠F=∠BAF,
∴∠F=∠DAF,
∴DF=AD=4.
故选:B.
10.解:有一个外角等于120°,即有一个内角等于60°,这样的等腰三角形是等边三角形,故①正确;
等腰三角形的一边长为4,另一边长为9,则第三边只能为9,这个等腰三角形的周长为22,故②错误;
两个单项式的积仍是单项式,故③正确;
形如的式子,当B中不含有字母时,不是分式,故④错误;
三角形两边垂直平分线的交点到三角形三个顶点的距离相等,故⑤错误;
∴正确的命题有①③,共2个,
故选:B.
二、填空题(共18分)
11.解:∵分式有意义的条件是分母不等于0,
∴x﹣1≠0,解得x≠1,
故答案为:x≠1.
12.解:ma2﹣4mb2
=m(a2﹣4b2)
=m(a+2b)(a﹣2b),
故答案为:m(a+2b)(a﹣2b).
13.解:原式=4a2﹣2a+1.
故答案为:4a2﹣2a+1.
14.解:∵AB=AC,
∴∠B=∠C=80°,
∴∠A=180°﹣∠B﹣∠C=20°,
故答案为:20°.
15.解:∵x2+mx+9
=x2+mx+(±3)2
=(x±3)2,
∴m=2×1×(±#)=±6,
故答案为:±6.
16.解:作BM⊥CF于点M,CN⊥BN于点N,
∴∠BMF=∠CNE=90°,
∵点D为BC边的中点,DP⊥BC,
∴PB=PC,
∴∠PBC=∠PCB,
∵BP=CP,∠BMP=∠CNP,且∠BPM=∠CPN,
∴△BPM≌△CPN(AAS),
∴BM=CN,PM=PN,S△BPM=S△CPN,
∵∠A=∠BPF=60°,
∴∠BFP=∠BEA,
∵∠BEA=∠CEN,
∴∠CEN=∠BFP,
在△BFM和△CEN中,
,
∴△BFM≌△CEN(AAS),
∴FM=NE,S△BFM=S△CEN,
∴S△PBF+S△PCE=2S△BPM,
∵∠BPF=60°,BP=CP,
∴∠PBD=∠PCD=30°,
∴∠MBP=∠PBD=30°,且BP=BP,∠BMP=∠BDP=90°,
∴△BMP≌△BDP(AAS),
∴,
∴,
故答案为:.
三、解答题(满分72分)
17.解:(1)p(a2+b2)﹣q(a2+b2)
=(a2+b2)(p﹣q);
(2)(a+b)2﹣12(a+b)+36
=(a+b﹣6)2.
18.解:(1)原式=﹣a10b8÷a3b3
=﹣a7b5;
(2)原式=982+2×98×2+22
=(98+2)2
=1002
=10000.
19.解:原式=x3﹣x2﹣x3﹣x2+x
=﹣2x2+x,
∵x=20220﹣=1﹣=,
∴原式=﹣2×()2+=0.
20.解:(1)如图所示,△A'B'C'即为所求;
(2)线段CC′被直线l垂直平分.
故答案为:垂直平分;
(3)连接BC′交直线l于点P,则点P即为所求点.
21.解:∵CD是△ABC的中线,AB=8,
∴AD=BD=AB=×8=4,
∵△ABC沿CD折叠,使点A落在点E处,
∴AD=DE,∠ADC=∠EDC=60°,
∴DE=DB,
∵∠BDE=180°﹣∠ADC﹣∠EDC=60°,
∴△EDB是等边三角形,
∴BE=BD=4.
22.解:∵(2n+1)2﹣(2n﹣1)2=[(2n+1)+(2n﹣1)][(2n+1)﹣(2n﹣1)]
=4n×2
=8n,
∴当n是整数时,两个连续奇数的平方差(2n+1)2﹣(2n﹣1)2是8的倍数.
23.证明:∵AC=BC,
∴∠CAB=∠CBA,
∵△AEC和△BCD为等边三角形,
∴∠CAE=∠CBD,∠FAG=∠FBG,
∴AF=BF.
在△AFC和△BFC中,
,
∴△AFC≌△BFC(SSS),
∴∠ACF=∠BCF,
即CF平分∠ACB,
又∵AC=BC,
∴AG=BG,
即G为AB的中点.
24.解:(1)b2+ab=b(b+a),
故答案为:b(b+a);
(2)a2+3ab+2b2=(a+b)(a+2b),
故答案为:(a+b)(a+2b);
(3)a2+4b2+4ab=(a+2b)2,
a2+4b2+5ab=(a+b)(a+4b),
25.(1)解:∵等边△ABC,
∴AB=CA,∠BAE=∠ACD=60°,
在△ACD与△BAE中,
,
∴△ACD≌△BAE(SAS),
∴∠DAC=∠EBA,
∵∠BFD=∠BAF+∠ABF,
∴∠BFD=∠BAF+∠CAD=∠BAC=60°.
(2)证明:在BF上截取BQ=AF,连接AQ,
在△QBA与△FAC中,
,
∴△QBA≌△FAC(SAS),
∴∠BAQ=∠ACF,
∴∠QBA+∠BAQ=∠DAC+∠BAQ=∠DAC+∠ACF,
∵∠AQF=∠QBA+∠BAQ,∠DFC=∠DAC+∠ACF,
∴∠AQF=∠DFC=∠BAQ+∠DAC.
∵CF⊥BE,∠BFD=60°,
∴∠AQF=∠DFC=∠BAQ+∠DAC=30°,
∴∠AQF=∠DFC=∠QAF=30°,
∴AF=FQ,
∴AF=FQ=BQ,
∵BF=FQ+BQ=2FQ,
∴BF=2AF.
(3)解:如图,延长BE到点N,使得AF=FN,连接AN,连接CN,交FH于点M,
∵∠BFD=∠AFN=60°,
∴△AFN是等边三角形,
∴AF=AN=FN,∠FAN=∠FNA=∠AFN=60°,
∴∠BAF=60°﹣∠FAE=∠CAN,
在△BAF与△CAN中,
,
∴△BAF≌△CAN(SAS),
∴BF=CN,∠ABF=∠ACN,
∵∠DAC=∠EBA,
∴∠DAC=∠ACN,
∴CN∥AD,
∴∠AFN=∠FNM=60°,
∵CF⊥BE,
∴∠FCN=30°,
∵∠DFC=30°,AD沿CF翻折交AC于点G,CF⊥CH,
∴∠DFC=∠MFC=∠MCF=30°,∠MFN=∠MCH=∠MHC=60°,
∴MF=MC,∠CMH=∠FMN=60°,
∴△MCF是等腰三角形,△CMH,△MFN是等边三角形,
∴AF=AN=CM=HM=MF=MN=FN,
∵BF=4,BF=2AF,
∴AF=2=AN=CM=HM=MF=MN=FN;
在△AGF与△CGM中,
,
∴△AGF≌△CGM(SAS),
∴,
∴GH=HM+MG=2+1=3.
