苏科版八年级数学上册2.5等腰三角形的轴对称性 学案(无答案)
文档属性
| 名称 | 苏科版八年级数学上册2.5等腰三角形的轴对称性 学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 631.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-03 18:59:18 | ||
图片预览


文档简介
2.5等腰三角形的轴对称性
(压轴题型提优练习)
【学习目标】
掌握等腰(边)三角形的综合求边长关系
2.掌握等腰三角形的动点问题
3. 掌握等腰三角形的新定义题型
【典型例题】
类型一、等腰(边)三角形的综合求边长关系
【例1】【观察发现】
如图1,△ABC和△CDE都是等腰直角三角形,连接BD和AE,BD、AE相交于点P,猜想线段BD与AE的数量关系,以及BD与AE相交构成角的度数.请说明理由.
【深入探究】
如图2,△ABC和△CDE都是等腰直角三角形,且∠ACB=∠DCE=90°,连接AD、BE,Q为AD中点,连接QC.试探究线段CQ与BE的关系,并加以证明.
举一反三:
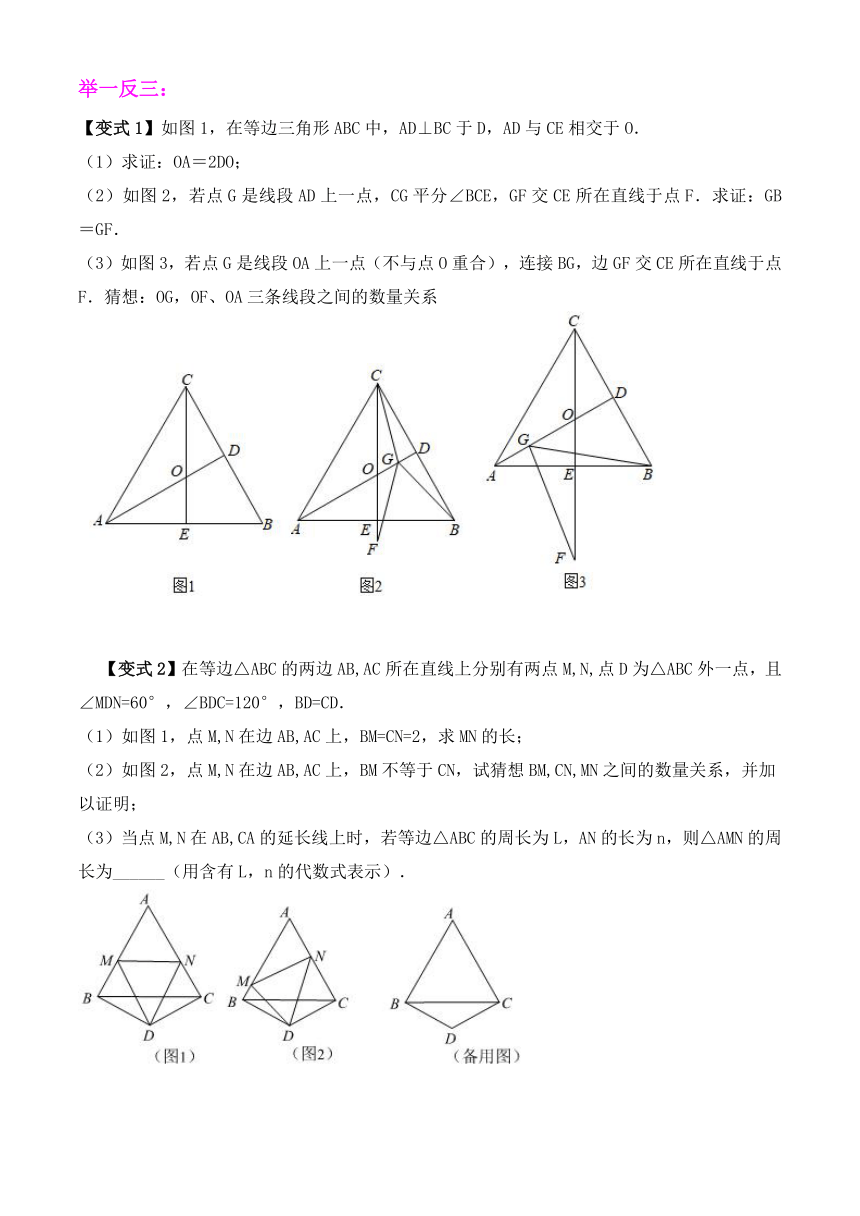
【变式1】如图1,在等边三角形ABC中,AD⊥BC于D,AD与CE相交于O.
(1)求证:OA=2DO;
(2)如图2,若点G是线段AD上一点,CG平分∠BCE,GF交CE所在直线于点F.求证:GB=GF.
(3)如图3,若点G是线段OA上一点(不与点O重合),连接BG,边GF交CE所在直线于点F.猜想:OG,OF、OA三条线段之间的数量关系
【变式2】在等边△ABC的两边AB,AC所在直线上分别有两点M,N,点D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=CD.
(1)如图1,点M,N在边AB,AC上,BM=CN=2,求MN的长;
(2)如图2,点M,N在边AB,AC上,BM不等于CN,试猜想BM,CN,MN之间的数量关系,并加以证明;
(3)当点M,N在AB,CA的延长线上时,若等边△ABC的周长为L,AN的长为n,则△AMN的周长为______(用含有L,n的代数式表示).
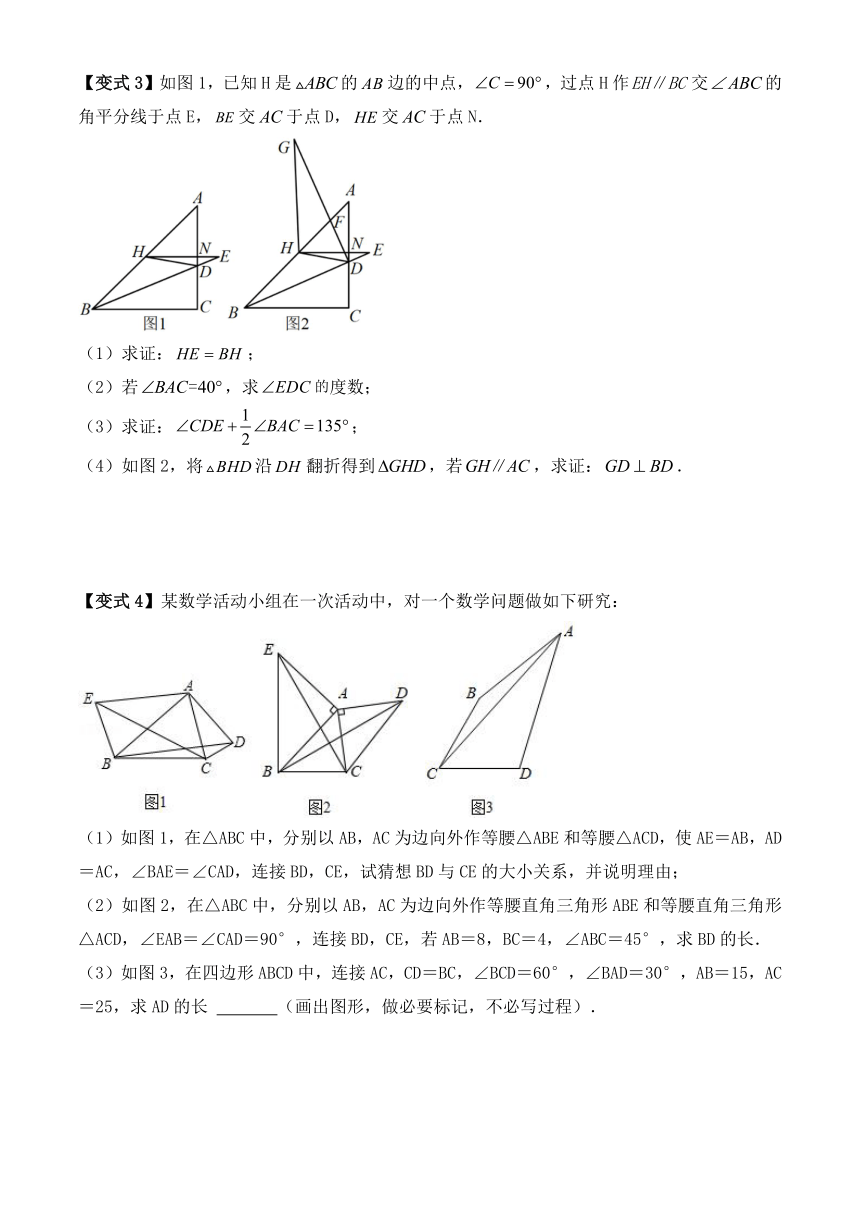
【变式3】如图1,已知H是的边的中点,,过点H作交的角平分线于点E,交于点D,交于点N.
(1)求证:;
(2)若,求度数;
(3)求证:;
(4)如图2,将沿翻折得到,若,求证:.
【变式4】某数学活动小组在一次活动中,对一个数学问题做如下研究:
(1)如图1,在△ABC中,分别以AB,AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由;
(2)如图2,在△ABC中,分别以AB,AC为边向外作等腰直角三角形ABE和等腰直角三角形△ACD,∠EAB=∠CAD=90°,连接BD,CE,若AB=8,BC=4,∠ABC=45°,求BD的长.
(3)如图3,在四边形ABCD中,连接AC,CD=BC,∠BCD=60°,∠BAD=30°,AB=15,AC=25,求AD的长 (画出图形,做必要标记,不必写过程).
类型二、等腰三角形的动点问题
【例1】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1)当t=1s时,求△ACP的面积.
(2)t为何值时,线段AP是∠CAB的平分线?
(3)请利用备用图2继续探索:当△ACP是等腰三角形时,求t的值.
举一反三:
【变式1】 如图1,中,于D,且,
(1)试说明是等腰三角形;
(2)已知,如图2,动点M从点B出发以每秒的速度沿线段向点A运动,同时动点N从点A出发以相同速度沿线段向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),
①若的边与平行,求t的值;
②若点E是边的中点,问在点M运动的过程中,能否成为等腰三角形?若能,求出t的值;若不能,请说明理
【变式2】如图,在中,,点从点出发,以每秒个单位长度的速度沿折线运动,运动到点时停止.设点的运动时间为秒().
(1)求斜边上高.
(2)①当点在上时,长为_______.(用含的代数式表示)
②若点在的角平分线上,则的值为_______.
(3)在整个运动过程中,直接写出是等腰三角形时的值.
【变式3】如图,在△ABC中,∠B=90°,AB=16cm,BC=12cm,AC=20cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)BP=______(用t的代数式表示)
(2)当点Q在边BC上运动时,出发几秒后,△PQB是等腰三角形?
(3)当点Q在边CA上运动时,出发__________________秒后,△BCQ是以BC或BQ为底边等腰三角形?
【变式4】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.
类型三、等腰三角形的新定义题型
【例1】如果一条线段将一个三角形分割成 2 个小等腰三角形,我们把这条线段叫做这个三角形的“好线”;如果两条线段将一个三角形分割成 3 个小等腰三角形,我们把这两条线段叫做这个三角形的“好好线”.
(1)如图,在 中,,点 D 在边上,且,则_____度;
(2)在 中,和是 的“好好线”,点 D 在 边上,点 E 在 边上,且,,则的度数为____________.
举一反三:
【变式1】定义:如果两条线段将一个三角形分成 3个等腰三角形,我们把这两条线段叫做这个三角形的“三分线”.例如:如图①,线段、把一个顶角为的等腰分成了 3个等腰三角形,则线段、就是等腰的“三分线”.
(1)图②是一个顶角为 45°的等腰三角形,在图中画出“三分线”,并标出每个等腰三角形顶角的度数.
(2)如图③,在边上取一点,令可以分割出第一个等腰,接着又需要考虑如何将分成2个等腰三角形,即可画出所需要的“三分线”,类比该方法,在图④中画出的“三分线”,并标出每个等腰三角形顶角的度数;
【变式2】数学课上,同学们探究下面命题的正确性,顶角为36°的等腰三角形我们称之为黄金三角形,“黄金三角形“具有一种特性,即经过它某一顶点的一条直线可以把它分成两个小等腰三角形,为此,请你,解答问题:
(1)已知如图1:黄金三角形△ABC中,∠A=36°,直线BD平分∠ABC交AC于点D,求证:△ABD和△DBC都是等腰三角形;
(2)如图,在△ABC中,AB=AC,∠A=36°,请你设计三种不同的方法,将△ABC分割成三个等腰三角形,不要求写出画法,不要求证明,但是要标出所分得的每个三角形的各内角的度数.
(3)已知一个三角形可以被分成两个等腰三角形,若原三角形的一个内角为36°,求原三角形的最大内角的所有可能值.
【变式3】若和△ADE均为等腰三角形,且,当和互余时,称与△ADE互为“底余等腰三角形”,的边上的高叫做△ADE的“余高”如图,与△ADE互为“底余等腰三角形”.
(1)若连接,,判断与是否互为“底余等腰三角形”:______(填“是”或“否”);
(2)当时,若△ADE的“余高”,则______;
(3)当时,判断与之间的数量关系,并说明理由.
(压轴题型提优练习)
【学习目标】
掌握等腰(边)三角形的综合求边长关系
2.掌握等腰三角形的动点问题
3. 掌握等腰三角形的新定义题型
【典型例题】
类型一、等腰(边)三角形的综合求边长关系
【例1】【观察发现】
如图1,△ABC和△CDE都是等腰直角三角形,连接BD和AE,BD、AE相交于点P,猜想线段BD与AE的数量关系,以及BD与AE相交构成角的度数.请说明理由.
【深入探究】
如图2,△ABC和△CDE都是等腰直角三角形,且∠ACB=∠DCE=90°,连接AD、BE,Q为AD中点,连接QC.试探究线段CQ与BE的关系,并加以证明.
举一反三:
【变式1】如图1,在等边三角形ABC中,AD⊥BC于D,AD与CE相交于O.
(1)求证:OA=2DO;
(2)如图2,若点G是线段AD上一点,CG平分∠BCE,GF交CE所在直线于点F.求证:GB=GF.
(3)如图3,若点G是线段OA上一点(不与点O重合),连接BG,边GF交CE所在直线于点F.猜想:OG,OF、OA三条线段之间的数量关系
【变式2】在等边△ABC的两边AB,AC所在直线上分别有两点M,N,点D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=CD.
(1)如图1,点M,N在边AB,AC上,BM=CN=2,求MN的长;
(2)如图2,点M,N在边AB,AC上,BM不等于CN,试猜想BM,CN,MN之间的数量关系,并加以证明;
(3)当点M,N在AB,CA的延长线上时,若等边△ABC的周长为L,AN的长为n,则△AMN的周长为______(用含有L,n的代数式表示).
【变式3】如图1,已知H是的边的中点,,过点H作交的角平分线于点E,交于点D,交于点N.
(1)求证:;
(2)若,求度数;
(3)求证:;
(4)如图2,将沿翻折得到,若,求证:.
【变式4】某数学活动小组在一次活动中,对一个数学问题做如下研究:
(1)如图1,在△ABC中,分别以AB,AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由;
(2)如图2,在△ABC中,分别以AB,AC为边向外作等腰直角三角形ABE和等腰直角三角形△ACD,∠EAB=∠CAD=90°,连接BD,CE,若AB=8,BC=4,∠ABC=45°,求BD的长.
(3)如图3,在四边形ABCD中,连接AC,CD=BC,∠BCD=60°,∠BAD=30°,AB=15,AC=25,求AD的长 (画出图形,做必要标记,不必写过程).
类型二、等腰三角形的动点问题
【例1】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1)当t=1s时,求△ACP的面积.
(2)t为何值时,线段AP是∠CAB的平分线?
(3)请利用备用图2继续探索:当△ACP是等腰三角形时,求t的值.
举一反三:
【变式1】 如图1,中,于D,且,
(1)试说明是等腰三角形;
(2)已知,如图2,动点M从点B出发以每秒的速度沿线段向点A运动,同时动点N从点A出发以相同速度沿线段向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),
①若的边与平行,求t的值;
②若点E是边的中点,问在点M运动的过程中,能否成为等腰三角形?若能,求出t的值;若不能,请说明理
【变式2】如图,在中,,点从点出发,以每秒个单位长度的速度沿折线运动,运动到点时停止.设点的运动时间为秒().
(1)求斜边上高.
(2)①当点在上时,长为_______.(用含的代数式表示)
②若点在的角平分线上,则的值为_______.
(3)在整个运动过程中,直接写出是等腰三角形时的值.
【变式3】如图,在△ABC中,∠B=90°,AB=16cm,BC=12cm,AC=20cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)BP=______(用t的代数式表示)
(2)当点Q在边BC上运动时,出发几秒后,△PQB是等腰三角形?
(3)当点Q在边CA上运动时,出发__________________秒后,△BCQ是以BC或BQ为底边等腰三角形?
【变式4】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.
类型三、等腰三角形的新定义题型
【例1】如果一条线段将一个三角形分割成 2 个小等腰三角形,我们把这条线段叫做这个三角形的“好线”;如果两条线段将一个三角形分割成 3 个小等腰三角形,我们把这两条线段叫做这个三角形的“好好线”.
(1)如图,在 中,,点 D 在边上,且,则_____度;
(2)在 中,和是 的“好好线”,点 D 在 边上,点 E 在 边上,且,,则的度数为____________.
举一反三:
【变式1】定义:如果两条线段将一个三角形分成 3个等腰三角形,我们把这两条线段叫做这个三角形的“三分线”.例如:如图①,线段、把一个顶角为的等腰分成了 3个等腰三角形,则线段、就是等腰的“三分线”.
(1)图②是一个顶角为 45°的等腰三角形,在图中画出“三分线”,并标出每个等腰三角形顶角的度数.
(2)如图③,在边上取一点,令可以分割出第一个等腰,接着又需要考虑如何将分成2个等腰三角形,即可画出所需要的“三分线”,类比该方法,在图④中画出的“三分线”,并标出每个等腰三角形顶角的度数;
【变式2】数学课上,同学们探究下面命题的正确性,顶角为36°的等腰三角形我们称之为黄金三角形,“黄金三角形“具有一种特性,即经过它某一顶点的一条直线可以把它分成两个小等腰三角形,为此,请你,解答问题:
(1)已知如图1:黄金三角形△ABC中,∠A=36°,直线BD平分∠ABC交AC于点D,求证:△ABD和△DBC都是等腰三角形;
(2)如图,在△ABC中,AB=AC,∠A=36°,请你设计三种不同的方法,将△ABC分割成三个等腰三角形,不要求写出画法,不要求证明,但是要标出所分得的每个三角形的各内角的度数.
(3)已知一个三角形可以被分成两个等腰三角形,若原三角形的一个内角为36°,求原三角形的最大内角的所有可能值.
【变式3】若和△ADE均为等腰三角形,且,当和互余时,称与△ADE互为“底余等腰三角形”,的边上的高叫做△ADE的“余高”如图,与△ADE互为“底余等腰三角形”.
(1)若连接,,判断与是否互为“底余等腰三角形”:______(填“是”或“否”);
(2)当时,若△ADE的“余高”,则______;
(3)当时,判断与之间的数量关系,并说明理由.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
