人教版数学九年级上册第二十四章圆 检测题(含答案)
文档属性
| 名称 | 人教版数学九年级上册第二十四章圆 检测题(含答案) | 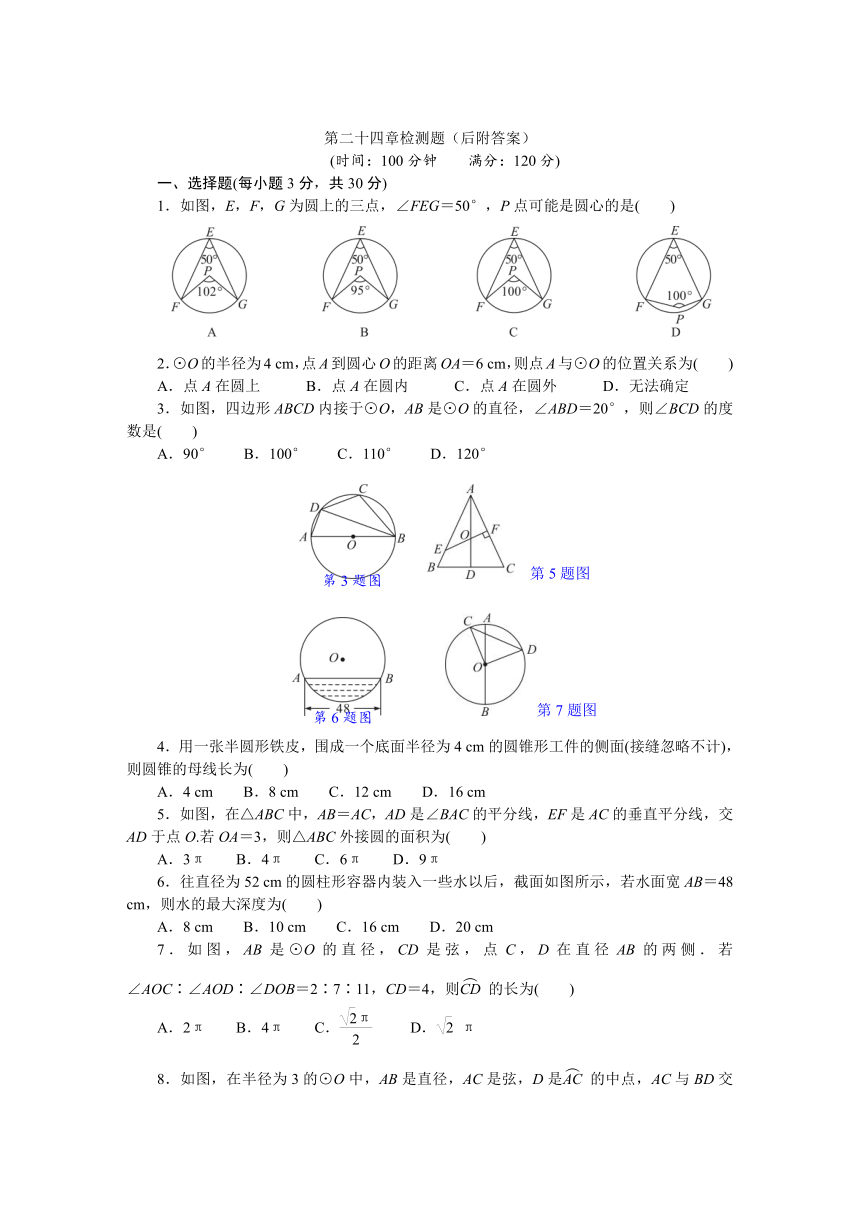 | |
| 格式 | DOC | ||
| 文件大小 | 815.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-03 19:18:44 | ||
图片预览

文档简介
第二十四章检测题(后附答案)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如图,E,F,G为圆上的三点,∠FEG=50°,P点可能是圆心的是( )
2.⊙O的半径为4 cm,点A到圆心O的距离OA=6 cm,则点A与⊙O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
3.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠ABD=20°,则∠BCD的度数是( )
A.90° B.100° C.110° D.120°
eq \o(\s\up7(),\s\do5(第3题图)) 第5题图
eq \o(\s\up7(),\s\do5(第6题图)) 第7题图
4.用一张半圆形铁皮,围成一个底面半径为4 cm的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为( )
A.4 cm B.8 cm C.12 cm D.16 cm
5.如图,在△ABC中,AB=AC,AD是∠BAC的平分线,EF是AC的垂直平分线,交AD于点O.若OA=3,则△ABC外接圆的面积为( )
A.3π B.4π C.6π D.9π
6.往直径为52 cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48 cm,则水的最大深度为( )
A.8 cm B.10 cm C.16 cm D.20 cm
7.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC∶∠AOD∶∠DOB=2∶7∶11,CD=4,则的长为( )
A.2π B.4π C. D.π
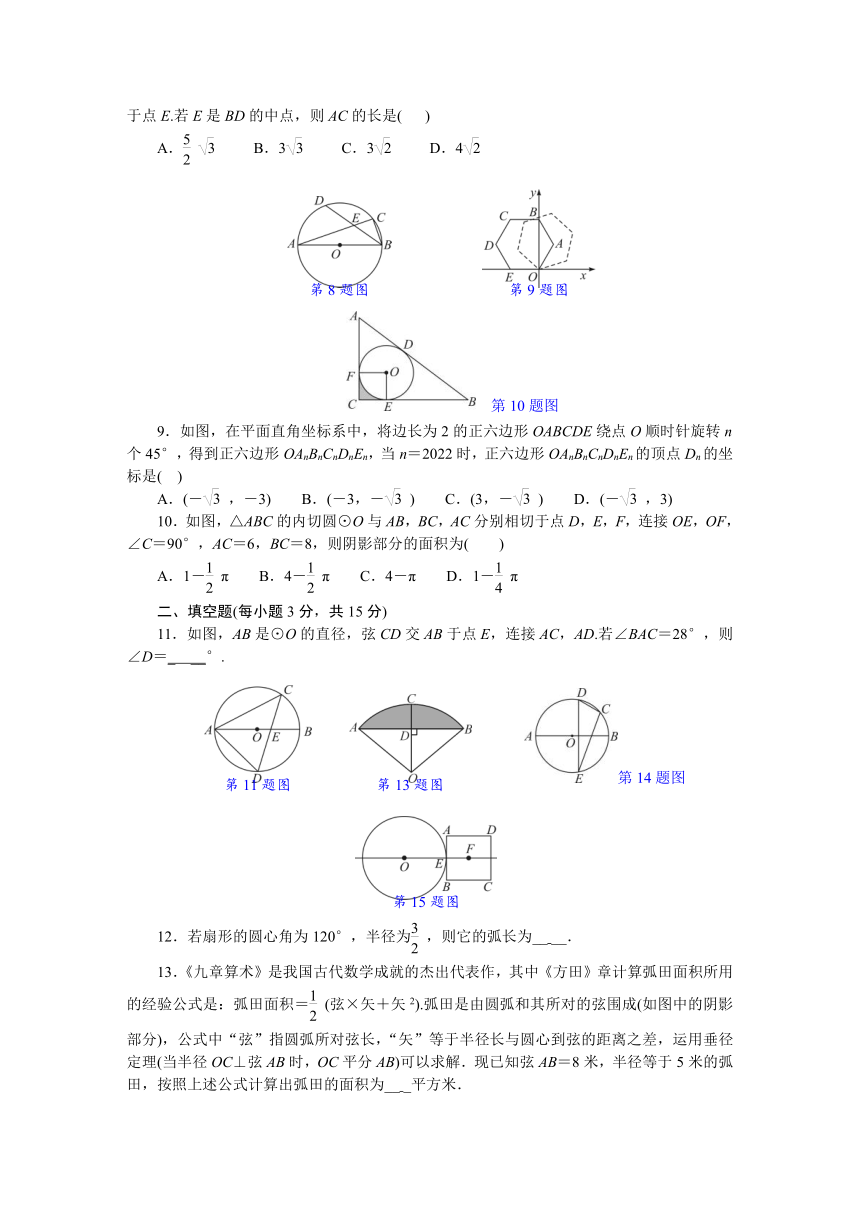
8.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A. B.3 C.3 D.4
eq \o(\s\up7(),\s\do5(第8题图)) eq \o(\s\up7(),\s\do5(第9题图))
第10题图
9.如图,在平面直角坐标系中,将边长为2的正六边形OABCDE绕点O顺时针旋转n个45°,得到正六边形OAnBnCnDnEn,当n=2022时,正六边形OAnBnCnDnEn的顶点Dn的坐标是( )
A.(-,-3) B.(-3,-) C.(3,-) D.(-,3)
10.如图,△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,连接OE,OF,∠C=90°,AC=6,BC=8,则阴影部分的面积为( )
A.1-π B.4-π C.4-π D.1-π
二、填空题(每小题3分,共15分)
11.如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD.若∠BAC=28°,则∠D=_ __°.
eq \o(\s\up7(),\s\do5(第11题图)) eq \o(\s\up7(),\s\do5(第13题图)) 第14题图 eq \o(\s\up7(),\s\do5(第15题图))
12.若扇形的圆心角为120°,半径为,则它的弧长为__ __.
13.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积=(弦×矢+矢2).弧田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径OC⊥弦AB时,OC平分AB)可以求解.现已知弦AB=8米,半径等于5米的弧田,按照上述公式计算出弧田的面积为__ _平方米.
14.如图,点A,B,C,D均在⊙O上,直径AB=4,点C是的中点,点D关于AB对称的点为E,若∠DCE=100°,则弦CE的长是__ __.
15.如图,半径为2 cm的⊙O与边长为2 cm的正方形ABCD的边AB相切于点E,点F为正方形的中心,直线OE过F点.当正方形ABCD沿直线OF以每秒(2-)cm的速度向左运动__ __秒时,⊙O与正方形重叠部分的面积为(π-)cm2.
三、解答题(共75分)
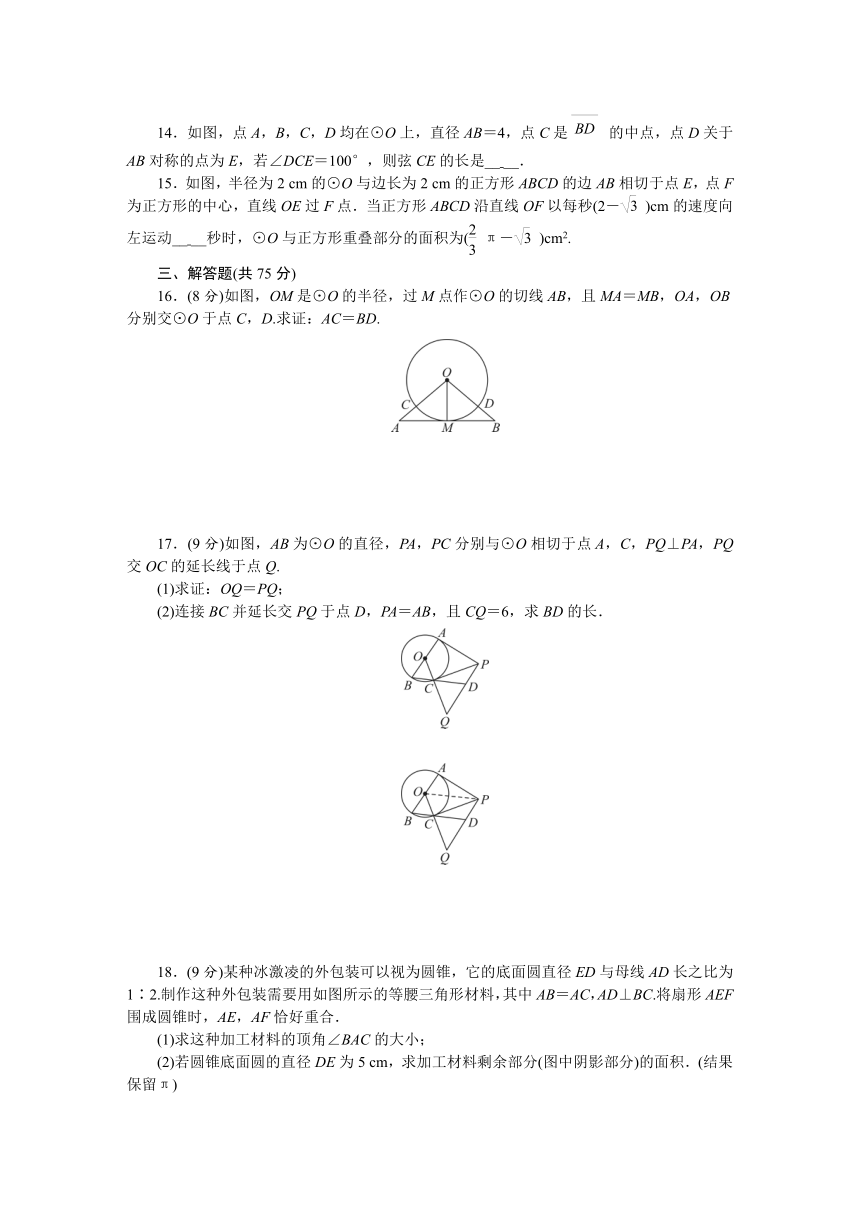
16.(8分)如图,OM是⊙O的半径,过M点作⊙O的切线AB,且MA=MB,OA,OB分别交⊙O于点C,D.求证:AC=BD.
17.(9分)如图,AB为⊙O的直径,PA,PC分别与⊙O相切于点A,C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连接BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
18.(9分)某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED与母线AD长之比为1∶2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB=AC,AD⊥BC.将扇形AEF围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小;
(2)若圆锥底面圆的直径DE为5 cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)
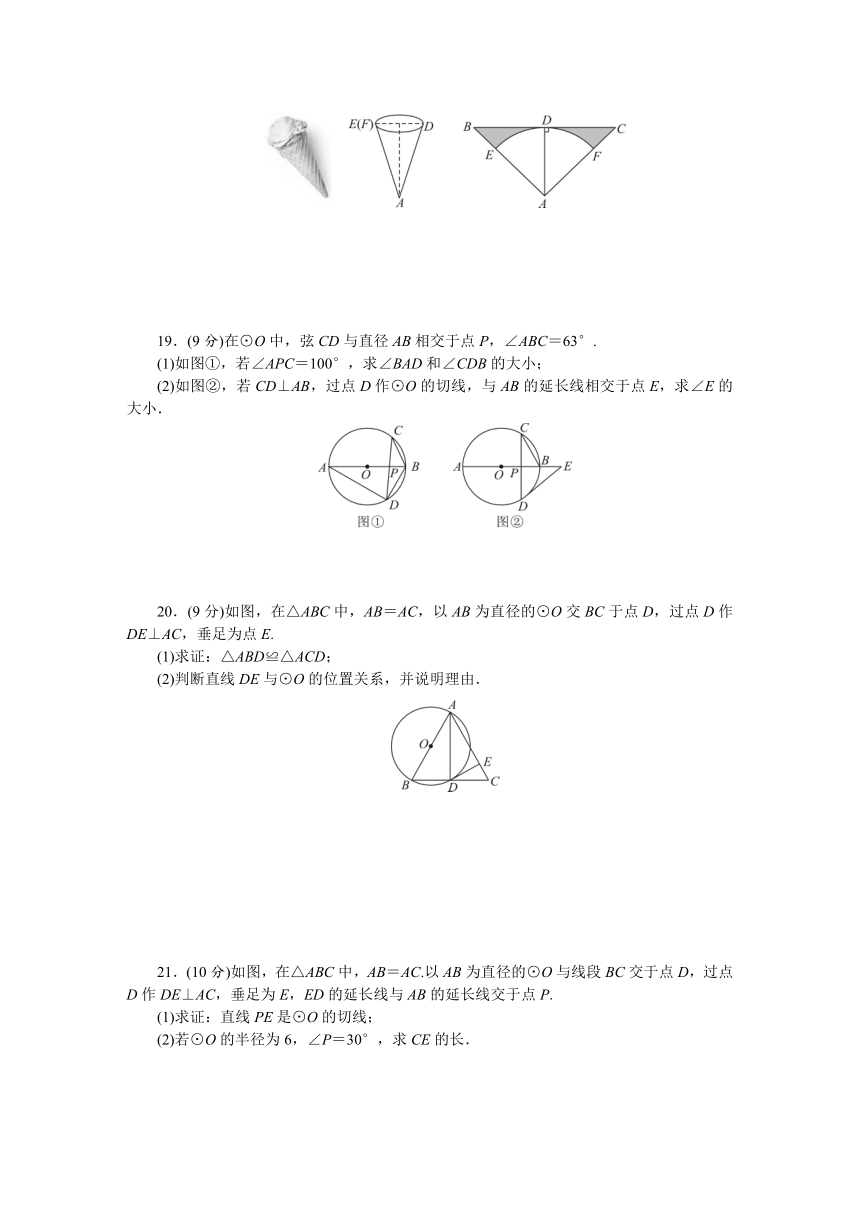
19.(9分)在⊙O中,弦CD与直径AB相交于点P,∠ABC=63°.
(1)如图①,若∠APC=100°,求∠BAD和∠CDB的大小;
(2)如图②,若CD⊥AB,过点D作⊙O的切线,与AB的延长线相交于点E,求∠E的大小.
20.(9分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为点E.
(1)求证:△ABD≌△ACD;
(2)判断直线DE与⊙O的位置关系,并说明理由.
21.(10分)如图,在△ABC中,AB=AC.以AB为直径的⊙O与线段BC交于点D,过点D作DE⊥AC,垂足为E,ED的延长线与AB的延长线交于点P.
(1)求证:直线PE是⊙O的切线;
(2)若⊙O的半径为6,∠P=30°,求CE的长.
22.(10分)如图,AB为半圆O的直径,点C为半圆上任一点.
(1)若∠BAC=30°,过点C作半圆O的切线交直线AB于点P.求证:△PBC≌△AOC;
(2)若AB=6,过点C作AB的平行线交半圆O于点D.当以点A,O,C,D为顶点的四边形为菱形时,求的长.
23.(11分)在平面直角坐标系xOy中,⊙O的半径为1.对于点A和线段BC,给出如下定义:若将线段BC绕点A旋转可以得到⊙O的弦B′C′(B′,C′分别是B,C的对应点),则称线段BC是⊙O的以点A为中心的“关联线段”.
(1)如图,点A,B1,C1,B2,C2,B3,C3的横、纵坐标都是整数.在线段B1C1,B2C2,B3C3中,⊙O的以点A为中心的“关联线段”是 __ _;
(2)△ABC是边长为1的等边三角形,点A(0,t),其中t≠0.若BC是⊙O的以点A为中心的“关联线段”,求t的值;
(3)在△ABC中,AB=1,AC=2.若BC是⊙O的以点A为中心的“关联线段”,直接写出OA的最小值和最大值,以及相应的BC长.
答案:
第二十四章检测题
(时间:100分钟 满分:120分)
1.( C )
2.( C )
3.( C )
4.( B )
5.( D )
6.( C )
7.( D )
8.( D )
9.( A )
10.( C )
11.__62__°.
12.__π__.
13.__10__平方米.
14.__2__.
15.__1或(11+6)__
16.
证明:∵OM是⊙O的半径,AB是⊙O的切线,∴OM⊥AB,∵MA=MB,∴OA=OB,∵OC=OD,∴OA-OC=OB-OD,即AC=BD
17.
解:(1)连接OP.∵PA,PC分别与⊙O相切于点A,C,∴PA=PC,OA⊥PA,∵OA=OC,OP=OP,∴△OPA≌△OPC(SSS),∴∠AOP=∠POC,∵QP⊥PA,∴QP∥BA,∴∠QPO=∠AOP,∴∠QOP=∠QPO,∴OQ=PQ
(2)设OA=r.∵OB=OC,∴∠OBC=∠OCB,∵OB∥QD,∴∠QDC=∠B,∵∠OCB=∠QCD,∴∠QCD=∠QDC,∴QC=QD=6,∵QO=QP,∴OC=DP=r,∵PC是⊙O的切线,∴OC⊥PC,∴∠OCP=∠PCQ=90°,在Rt△PCQ中,∵PQ2=PC2+QC2,∴(6+r)2=62+(2r)2,r=4(r=0舍去),∴OP==4,∵OB=PD,OB∥PD,∴四边形OBDP是平行四边形,∴BD=OP=4
18.
解:(1)设∠BAC=n°.由题意得π·DE=,AD=2DE,∴n=90,∴∠BAC=90°
(2)∵AD=2DE=10 cm,∴BC=2AD=20 cm,S阴影=S△ABC-S扇形AEF=×20×10-=(100-25π) cm2
19.
解:(1)∵∠APC是△PBC的一个外角,∴∠C=∠APC-∠ABC=100°-63°=37°,由圆周角定理得:∠BAD=∠C=37°,∠ADC=∠ABC=63°,∵AB是⊙O的直径,∴∠ADB=90°,∴∠CDB=∠ADB-∠ADC=90°-63°=27°
(2)连接OD,∵CD⊥AB,∴∠CPB=90°,∴∠PCB=90°-∠ABC=90°-63°=27°,∵DE是⊙O的切线,∴DE⊥OD,∴∠ODE=90°,∵∠BOD=2∠PCB=54°,∴∠E=90°-∠BOD=90°-54°=36°
20.
解:
(1)∵AB为⊙O的直径,∴AD⊥BC,在Rt△ADB和Rt△ADC中,∴Rt△ABD≌Rt△ACD(HL)
(2)直线DE与⊙O相切,理由如下:连接OD,如图所示.由△ABD≌△ACD知:BD=DC,又∵OA=OB,∴OD为△ABC的中位线,∴OD∥AC,∵DE⊥AC,∴OD⊥DE,∵OD为⊙O的半径,∴DE与⊙O相切
21.
解:
(1)连接OD,如图.∵AB=AC,∴∠ABC=∠ACB,∵OB=OD,∴∠ABC=∠ODB,∴∠ACB=∠ODB,∴OD∥AC,∵DE⊥AC,∴DE⊥OD,即PE⊥OD,∵OD是⊙O的半径,∴PE是⊙O的切线
(2)连接AD,如图.∵DE⊥AC,∴∠AEP=90°,∵∠P=30°,∴∠PAE=60°,∵AB=AC,∴△ABC是等边三角形,∵⊙O的半径为6,∴BC=AB=12,∠C=60°,∵AB是⊙O的直径,∴∠ADB=90°,∴BD=CD=BC=6,在Rt△CDE中,∠C=60°,∴∠CDE=30°,∴CE=CD=3.答:CE的长是3
22.
解:(1)如图①,∵AB为半圆O的直径,∴∠ACB=90°,∵∠BAC=30°,∴∠ABC=60°,∵OB=OC,∴△OBC是等边三角形,∴OC=BC,∠OBC=∠BOC=60°,∴∠AOC=∠PBC=120°,∵CP是⊙O的切线,∴OC⊥PC,∴∠OCP=90°,∴∠ACO=∠PCB,在△AOC和△PBC中,∴△AOC≌△PBC(ASA)
(2)如图①,连接OD,AD,CD,∵四边形AOCD是菱形,∴OA=AD=CD=OC,∵OA=OD=OC,∴△AOD与△COD是等边三角形,∴∠AOD=∠COD=60°,∴∠BOC=60°,∴的长==π;如图②,同理∠BOC=120°,∴的长==2π,综上所述,的长为π或2π
23.(11分)(北京中考)在平面直角坐标系xOy中,⊙O的半径为1.对于点A和线段BC,给出如下定义:若将线段BC绕点A旋转可以得到⊙O的弦B′C′(B′,C′分别是B,C的对应点),则称线段BC是⊙O的以点A为中心的“关联线段”.
(1)如图,点A,B1,C1,B2,C2,B3,C3的横、纵坐标都是整数.在线段B1C1,B2C2,B3C3中,⊙O的以点A为中心的“关联线段”是 __B2C2__;
(2)△ABC是边长为1的等边三角形,点A(0,t),其中t≠0.若BC是⊙O的以点A为中心的“关联线段”,求t的值;
(3)在△ABC中,AB=1,AC=2.若BC是⊙O的以点A为中心的“关联线段”,直接写出OA的最小值和最大值,以及相应的BC长.
解:(2)设BC绕点A旋转后得到⊙O的弦B′C′,则B′C′=BC,AB′=AB,AC′=AC.∵△ABC是边长为1的等边三角形,∵△AB′C′也是边长为1的等边三角形.∵OB′=OC′=1,∴△OB′C′是边长为1的等边三角形.∵t≠0,∴点A与点O不重合.∴四边形AB′OC′是菱形.由OB′=1,∠B′OC′=60°,可得OA=.∴t=±
(3)OA的最小值是1,相应的BC长为;OA的最大值是2,相应的BC长为.理由:若BC是⊙O的以点A为中心的“关联线段”,则点B′,C′都在⊙O上,且AB′=AB=1,AC′=AC=2.易知当点A在⊙O上,OA的值最小且最小值为1,此时AC′为⊙O的直径,∴∠AB′C′=90°,∵AB′=1,∴BC=B′C′==.易知,当点A,B′,O三点共线时,OA的值最大且最大值为2,如图所示.
连接OC′,过点C′作C′P⊥OA于点P,∴OC′=1,AC′=OA=2.设OP=x(x>0),则AP=2-x,由勾股定理得C′P2=AC′2-AP2=OC′2-OP2,即22-(2-x)2=1-x2,解得x=,∴C′P==,B′P=OB′-OP=.在Rt△B′PC′中,B′C′==,∴BC=.综上所述,OA的最小值为1,此时BC=;OA的最大值为2,此时BC=
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如图,E,F,G为圆上的三点,∠FEG=50°,P点可能是圆心的是( )
2.⊙O的半径为4 cm,点A到圆心O的距离OA=6 cm,则点A与⊙O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
3.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠ABD=20°,则∠BCD的度数是( )
A.90° B.100° C.110° D.120°
eq \o(\s\up7(),\s\do5(第3题图)) 第5题图
eq \o(\s\up7(),\s\do5(第6题图)) 第7题图
4.用一张半圆形铁皮,围成一个底面半径为4 cm的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为( )
A.4 cm B.8 cm C.12 cm D.16 cm
5.如图,在△ABC中,AB=AC,AD是∠BAC的平分线,EF是AC的垂直平分线,交AD于点O.若OA=3,则△ABC外接圆的面积为( )
A.3π B.4π C.6π D.9π
6.往直径为52 cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48 cm,则水的最大深度为( )
A.8 cm B.10 cm C.16 cm D.20 cm
7.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC∶∠AOD∶∠DOB=2∶7∶11,CD=4,则的长为( )
A.2π B.4π C. D.π
8.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E.若E是BD的中点,则AC的长是( )
A. B.3 C.3 D.4
eq \o(\s\up7(),\s\do5(第8题图)) eq \o(\s\up7(),\s\do5(第9题图))
第10题图
9.如图,在平面直角坐标系中,将边长为2的正六边形OABCDE绕点O顺时针旋转n个45°,得到正六边形OAnBnCnDnEn,当n=2022时,正六边形OAnBnCnDnEn的顶点Dn的坐标是( )
A.(-,-3) B.(-3,-) C.(3,-) D.(-,3)
10.如图,△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,连接OE,OF,∠C=90°,AC=6,BC=8,则阴影部分的面积为( )
A.1-π B.4-π C.4-π D.1-π
二、填空题(每小题3分,共15分)
11.如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD.若∠BAC=28°,则∠D=_ __°.
eq \o(\s\up7(),\s\do5(第11题图)) eq \o(\s\up7(),\s\do5(第13题图)) 第14题图 eq \o(\s\up7(),\s\do5(第15题图))
12.若扇形的圆心角为120°,半径为,则它的弧长为__ __.
13.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积=(弦×矢+矢2).弧田是由圆弧和其所对的弦围成(如图中的阴影部分),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,运用垂径定理(当半径OC⊥弦AB时,OC平分AB)可以求解.现已知弦AB=8米,半径等于5米的弧田,按照上述公式计算出弧田的面积为__ _平方米.
14.如图,点A,B,C,D均在⊙O上,直径AB=4,点C是的中点,点D关于AB对称的点为E,若∠DCE=100°,则弦CE的长是__ __.
15.如图,半径为2 cm的⊙O与边长为2 cm的正方形ABCD的边AB相切于点E,点F为正方形的中心,直线OE过F点.当正方形ABCD沿直线OF以每秒(2-)cm的速度向左运动__ __秒时,⊙O与正方形重叠部分的面积为(π-)cm2.
三、解答题(共75分)
16.(8分)如图,OM是⊙O的半径,过M点作⊙O的切线AB,且MA=MB,OA,OB分别交⊙O于点C,D.求证:AC=BD.
17.(9分)如图,AB为⊙O的直径,PA,PC分别与⊙O相切于点A,C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连接BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
18.(9分)某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED与母线AD长之比为1∶2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB=AC,AD⊥BC.将扇形AEF围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小;
(2)若圆锥底面圆的直径DE为5 cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)
19.(9分)在⊙O中,弦CD与直径AB相交于点P,∠ABC=63°.
(1)如图①,若∠APC=100°,求∠BAD和∠CDB的大小;
(2)如图②,若CD⊥AB,过点D作⊙O的切线,与AB的延长线相交于点E,求∠E的大小.
20.(9分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为点E.
(1)求证:△ABD≌△ACD;
(2)判断直线DE与⊙O的位置关系,并说明理由.
21.(10分)如图,在△ABC中,AB=AC.以AB为直径的⊙O与线段BC交于点D,过点D作DE⊥AC,垂足为E,ED的延长线与AB的延长线交于点P.
(1)求证:直线PE是⊙O的切线;
(2)若⊙O的半径为6,∠P=30°,求CE的长.
22.(10分)如图,AB为半圆O的直径,点C为半圆上任一点.
(1)若∠BAC=30°,过点C作半圆O的切线交直线AB于点P.求证:△PBC≌△AOC;
(2)若AB=6,过点C作AB的平行线交半圆O于点D.当以点A,O,C,D为顶点的四边形为菱形时,求的长.
23.(11分)在平面直角坐标系xOy中,⊙O的半径为1.对于点A和线段BC,给出如下定义:若将线段BC绕点A旋转可以得到⊙O的弦B′C′(B′,C′分别是B,C的对应点),则称线段BC是⊙O的以点A为中心的“关联线段”.
(1)如图,点A,B1,C1,B2,C2,B3,C3的横、纵坐标都是整数.在线段B1C1,B2C2,B3C3中,⊙O的以点A为中心的“关联线段”是 __ _;
(2)△ABC是边长为1的等边三角形,点A(0,t),其中t≠0.若BC是⊙O的以点A为中心的“关联线段”,求t的值;
(3)在△ABC中,AB=1,AC=2.若BC是⊙O的以点A为中心的“关联线段”,直接写出OA的最小值和最大值,以及相应的BC长.
答案:
第二十四章检测题
(时间:100分钟 满分:120分)
1.( C )
2.( C )
3.( C )
4.( B )
5.( D )
6.( C )
7.( D )
8.( D )
9.( A )
10.( C )
11.__62__°.
12.__π__.
13.__10__平方米.
14.__2__.
15.__1或(11+6)__
16.
证明:∵OM是⊙O的半径,AB是⊙O的切线,∴OM⊥AB,∵MA=MB,∴OA=OB,∵OC=OD,∴OA-OC=OB-OD,即AC=BD
17.
解:(1)连接OP.∵PA,PC分别与⊙O相切于点A,C,∴PA=PC,OA⊥PA,∵OA=OC,OP=OP,∴△OPA≌△OPC(SSS),∴∠AOP=∠POC,∵QP⊥PA,∴QP∥BA,∴∠QPO=∠AOP,∴∠QOP=∠QPO,∴OQ=PQ
(2)设OA=r.∵OB=OC,∴∠OBC=∠OCB,∵OB∥QD,∴∠QDC=∠B,∵∠OCB=∠QCD,∴∠QCD=∠QDC,∴QC=QD=6,∵QO=QP,∴OC=DP=r,∵PC是⊙O的切线,∴OC⊥PC,∴∠OCP=∠PCQ=90°,在Rt△PCQ中,∵PQ2=PC2+QC2,∴(6+r)2=62+(2r)2,r=4(r=0舍去),∴OP==4,∵OB=PD,OB∥PD,∴四边形OBDP是平行四边形,∴BD=OP=4
18.
解:(1)设∠BAC=n°.由题意得π·DE=,AD=2DE,∴n=90,∴∠BAC=90°
(2)∵AD=2DE=10 cm,∴BC=2AD=20 cm,S阴影=S△ABC-S扇形AEF=×20×10-=(100-25π) cm2
19.
解:(1)∵∠APC是△PBC的一个外角,∴∠C=∠APC-∠ABC=100°-63°=37°,由圆周角定理得:∠BAD=∠C=37°,∠ADC=∠ABC=63°,∵AB是⊙O的直径,∴∠ADB=90°,∴∠CDB=∠ADB-∠ADC=90°-63°=27°
(2)连接OD,∵CD⊥AB,∴∠CPB=90°,∴∠PCB=90°-∠ABC=90°-63°=27°,∵DE是⊙O的切线,∴DE⊥OD,∴∠ODE=90°,∵∠BOD=2∠PCB=54°,∴∠E=90°-∠BOD=90°-54°=36°
20.
解:
(1)∵AB为⊙O的直径,∴AD⊥BC,在Rt△ADB和Rt△ADC中,∴Rt△ABD≌Rt△ACD(HL)
(2)直线DE与⊙O相切,理由如下:连接OD,如图所示.由△ABD≌△ACD知:BD=DC,又∵OA=OB,∴OD为△ABC的中位线,∴OD∥AC,∵DE⊥AC,∴OD⊥DE,∵OD为⊙O的半径,∴DE与⊙O相切
21.
解:
(1)连接OD,如图.∵AB=AC,∴∠ABC=∠ACB,∵OB=OD,∴∠ABC=∠ODB,∴∠ACB=∠ODB,∴OD∥AC,∵DE⊥AC,∴DE⊥OD,即PE⊥OD,∵OD是⊙O的半径,∴PE是⊙O的切线
(2)连接AD,如图.∵DE⊥AC,∴∠AEP=90°,∵∠P=30°,∴∠PAE=60°,∵AB=AC,∴△ABC是等边三角形,∵⊙O的半径为6,∴BC=AB=12,∠C=60°,∵AB是⊙O的直径,∴∠ADB=90°,∴BD=CD=BC=6,在Rt△CDE中,∠C=60°,∴∠CDE=30°,∴CE=CD=3.答:CE的长是3
22.
解:(1)如图①,∵AB为半圆O的直径,∴∠ACB=90°,∵∠BAC=30°,∴∠ABC=60°,∵OB=OC,∴△OBC是等边三角形,∴OC=BC,∠OBC=∠BOC=60°,∴∠AOC=∠PBC=120°,∵CP是⊙O的切线,∴OC⊥PC,∴∠OCP=90°,∴∠ACO=∠PCB,在△AOC和△PBC中,∴△AOC≌△PBC(ASA)
(2)如图①,连接OD,AD,CD,∵四边形AOCD是菱形,∴OA=AD=CD=OC,∵OA=OD=OC,∴△AOD与△COD是等边三角形,∴∠AOD=∠COD=60°,∴∠BOC=60°,∴的长==π;如图②,同理∠BOC=120°,∴的长==2π,综上所述,的长为π或2π
23.(11分)(北京中考)在平面直角坐标系xOy中,⊙O的半径为1.对于点A和线段BC,给出如下定义:若将线段BC绕点A旋转可以得到⊙O的弦B′C′(B′,C′分别是B,C的对应点),则称线段BC是⊙O的以点A为中心的“关联线段”.
(1)如图,点A,B1,C1,B2,C2,B3,C3的横、纵坐标都是整数.在线段B1C1,B2C2,B3C3中,⊙O的以点A为中心的“关联线段”是 __B2C2__;
(2)△ABC是边长为1的等边三角形,点A(0,t),其中t≠0.若BC是⊙O的以点A为中心的“关联线段”,求t的值;
(3)在△ABC中,AB=1,AC=2.若BC是⊙O的以点A为中心的“关联线段”,直接写出OA的最小值和最大值,以及相应的BC长.
解:(2)设BC绕点A旋转后得到⊙O的弦B′C′,则B′C′=BC,AB′=AB,AC′=AC.∵△ABC是边长为1的等边三角形,∵△AB′C′也是边长为1的等边三角形.∵OB′=OC′=1,∴△OB′C′是边长为1的等边三角形.∵t≠0,∴点A与点O不重合.∴四边形AB′OC′是菱形.由OB′=1,∠B′OC′=60°,可得OA=.∴t=±
(3)OA的最小值是1,相应的BC长为;OA的最大值是2,相应的BC长为.理由:若BC是⊙O的以点A为中心的“关联线段”,则点B′,C′都在⊙O上,且AB′=AB=1,AC′=AC=2.易知当点A在⊙O上,OA的值最小且最小值为1,此时AC′为⊙O的直径,∴∠AB′C′=90°,∵AB′=1,∴BC=B′C′==.易知,当点A,B′,O三点共线时,OA的值最大且最大值为2,如图所示.
连接OC′,过点C′作C′P⊥OA于点P,∴OC′=1,AC′=OA=2.设OP=x(x>0),则AP=2-x,由勾股定理得C′P2=AC′2-AP2=OC′2-OP2,即22-(2-x)2=1-x2,解得x=,∴C′P==,B′P=OB′-OP=.在Rt△B′PC′中,B′C′==,∴BC=.综上所述,OA的最小值为1,此时BC=;OA的最大值为2,此时BC=
同课章节目录
