第三章整式及其加减复习课件
图片预览











文档简介
课件56张PPT。
第三章 整式的加减
复习课
用字母表示数1.长方形的周长是2a,宽为b,则它的面积为__________b(a-b)2. 将n减少5,再扩大4倍,最后结果为__________4(n-5)3.如果m是整数,那么与m相邻的两个整数的和为___________(m-1)+(m+1)7.一根绳子原长为1米,从第一天起每天折断它
的一半。推断第一天剩余的长度_____,第二天剩
余的长度_____…第n天剩余的长度_____米米米4.用字母n表示偶数为________奇数为___________5. a与b的差的平方的 是______ 6. a的立方与b的立方的和的2倍是______2n2n+11._____________________________________ 叫做代数式。用运算符号把数字与字母连接起来的式子2. 运算符号包括_________________加,减,乘,除,乘方判断哪些是代数式代数式的定义注意: 单独一个数或一个字母也是代数式。数字与数字相乘不能省乘号。例如:3×4一、书写含乘法运算的代数式
1.乘号省,要酌情
2.数相乘,不能省
3.数在前,字母后
4.带分数,要化假(a+b)×(m+n)=(a+b)(m+n)t×3常写作3t
(2a+b)×3常写作3(2a+b)二、书写含除法运算的代数式除号变,分数线
当代数式中出现含有字母的除法运算时,结果一般不用“÷”,而应改用分数线,其中被除数作分子,除数作分母。
如ah ÷7=三.书写带有单位名称的代数式
1.遇和差,括号加
如(3a-2b)千克不能写作3a-2b千克;
(t-2) ℃ 不能写作t -2 ℃.
2.是积商,直接放 若代数式是积或商的形式,无需加括号,直接在代数式后写上单位名称即可。
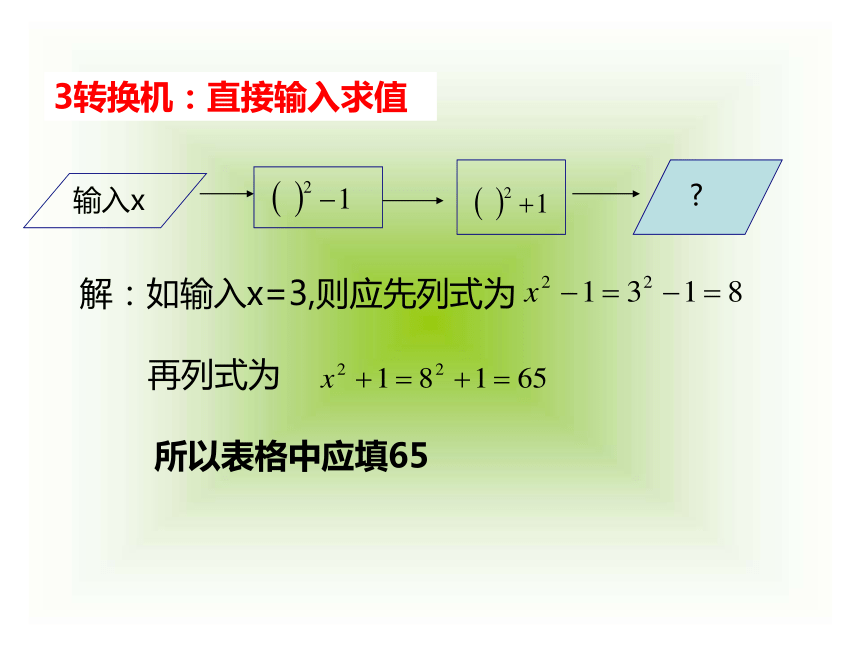
如(1+a%)a米,mn元。1、直接代入求值例1:当x=-2,y=-3时,求代数式 的值。解:当x=-2,y=-3时,2、整体代入求值1.解:2.已知 求代数式 的值。输入x解:如输入x=3,则应先列式为再列式为所以表格中应填653转换机:直接输入求值定义:单项式中的_________。次数:1.当单项式的系数是1或-1时,“1”通常省略不写。单项式:系数:数字或字母的乘积由_________________组成的式子。
单独的______或________也是单项式。单项式中的__________________.数字因数所有字母的指数和一个数一个字母注意的问题:2.当式子分母中出现字母时不是单项式。3.圆周率π是常数,不要看成字母。4.当单项式的系数是带分数时,通常写成假分数。5.单项式的系数应包括它前面的性质符号。6.单项式次数是指所有字母的次数的和,与数字的次数没有关系。7.单独的数字不含字母, 规定它的次数是零次.定义:几个__________.常数项:多项式中_______________.多项式的次数:_________________________.
项: 组成多项式中的_____________.
有几项,就叫做_________.1.在确定多项式的项时,要连同它前面的符号,
2.一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式。
3.在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念。多项式单项式的和每一个单项式几项式不含字母的项多项式中次数最高的项的次数。注意的问题:3、 的项是( ),次数是( ),
的项是( ),次数是( ),是( )次( )项式。2、 的系数是( ),次数是( ), 的系数是
( ),次数是( );1、在式子: 中,哪些是单项式,哪些是多项式?哪些是整式?y2、1-x-5xy2 、-x练 一练:y21-x-5xy2 21、-x、-5xy2 返回同类项的定义:(两相同)合并同类项概念:_________________________.合并同类项法则:2._________________不变。2._________________相同。1.____相同,字母相同的字母的指数也1.______相加减;字母和字母的指数系数同类项注意:几个常数项也是______同类项。(两无关)2.与__________无关。1.与____无关系数 字母的位置把多项式中的同类项合并成一项3、若5x2 y与是 x m yn同类项,则m=( ) n=( )
若5x2 y与 x m yn同的和是单项式, m=( ) n=( )1、下列各组是不是同类项:练一练:(1) 4abc 与 4ab (2) -5 m2 n3 与 2n3 m2(3) -0.3 x2 y 与 y x22、合并下列同类项:(1) 3xy – 4 xy – xy = ( ) (2) -a-a-2a=( ) 不是是是 –2xy –4a 2 12 12.若 与 是同类项,则m+n=___.4.若 ,则m+n-p=______543.若 与 的和是一个单项式,则 =___.-41.下列各式中,是同类项的是:___________① 与 ② 与 ③ 与 ⑤ 与 ⑥-125与③⑤⑥④ 与 整式的加减混合运算步骤(有括号先去括号)1.找同类项,做好标记。
2.利用加法的交换律和结合律把同类项放在一起。
3.利用乘法分配律计算结果。
4.按要求按“升”或“降”幂排列。找般并排 1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
“去括号,看符号。是‘+’号,不变号,是‘-’号,全变号”一:去括号二:计算(按照先小括号,再中括号,最后大括号的顺序)3、多项式 与 的和是 ,它们的差
是 ,多项式 减去一个多项 后是 ,则
这个多项式是 。1、去括号: 1) +(x-3)= 2) -(x-3)=
3)-(x+5y-2)= 4)+(3x-5y+6z)= 练一练:x-3-x+3- x- 5y+2 3x-5y+6z2、计算:(1)x-(-y -z+1)= ( 2 ) m+(-n+q)= ;
( 3 ) a - ( b+c-3)= ; ( 4 ) x+(5-3y)= 。
x-5xy2 -3x+xy2 -5a+4ab32ax+y +z -1m-n+qa-b-c+3x+5-3y-2x-4xy2 4x-6xy2 -7a+4ab34、化简已知,求解:跟踪练习:已知求2、已知1、求:(1)(2)例:两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50千米/时,水流速度是a千米/时。
(1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?解:顺水航速=船速+水速=50+a(千米/时)
顺水航速=船速-水速=50-a(千米/时)
跟踪练习:飞机的无风航速为a千米/时,风速为20千米/时,飞机顺风飞行6小时的行程是多少?飞机逆风飞行3小时的行程是多少?两个行程的相差是多少?(2)2小时后甲船比乙船多航行
2(50+a)-2(50-a)
=100+2a-100+2a
=4a(千米)(1) 2小时后两船相距
2(50+a)+2(50-a)
=100+2a+100-2a
=200(千米)一、填空:
1、a的倒数与b的相反数的差,用代数式表示是______.
2、a、b两数的平方差除a、b两数和的平方,所得商为_______.
3、一个两位数,个位上数字是x,十位上数字是个位数字的两倍,这个两位数是_______.
4、若3x 2m-1 y2与-2xy n-1是同类项,则2m-n= _______.
5、若x+y=6,则2- x-y的值是_______.
6、甲、乙两辆车同时从A、B两地相向而行,甲车速度为v千米/时,乙车速度是甲车的2倍还多2千米,若两车出发后4小时相遇,则A、B两地路程可以表示成__ _____ ;若v=40,则A、B两地路程是_____ 千米.巩固练习二、列代数式:1、已知长方形的宽为(2a-b)cm,长比宽多(a-b)cm,求这个长方形的周长。 3a2b - [2a2b -(2abc - a2c)- 4a2c ] – abc 四、求代数式
3a2b - [2a2b -(2abc - a2c)- 4a2c ] – abc的值,
其中a=-2,b=-3,c=1.三、化简:1.观察一列数:3,8,13,18,23,28,……,
依次规律,在数列中第2004个数是_____.2.下面一组按规律排列的数:2,4,8,16,
……,第2005个数应是_______.10018220053.按规律填数:(1)2,7,12,17,( ),( ),……(2)1,2,4,8,16,( ),( ),……4.观察下列算式:(1)第5个等式是___ ___ ;
(2)第n个等式是_______ _______ .-=4=1×4-=12=3×4-=20=5×4-=28=7×4按规律回答:22273264-=36=9×4-=(2n-1) ×45.如图,在2005年3月的日历上: 任意圈出一竖
列上相邻的三个
数,设中间的一个
数为x,则其余两
个数分别为
. x-7,x+7用火柴棒按下图的方式搭三角形 。③②①练一练⑴填写下表 :⑵照这样的规律搭下去,搭n个 这样的三角形需要多少根火柴棒?4n+159131721做一做:用棋子摆出下列一组图形:⑴摆第1个图形用_____枚棋子,摆第2个图形用_____枚棋子,摆第3个图形用______枚棋子;
⑵按照这种方式摆下去,摆第n个图形用_____枚棋子,摆第100个图形用_______枚棋子。3693n3001.探索规律并填空:
(1) .....
。 思考:(2)计算: .1.求当x= 时,多项式的值。解:原式===把x= 带入 中,得 ∴ 原式=5补充例题:化简下列式子:∴原式=-a-2[-(a+b)]-3(b-a)解:由题意知:a<0,b>0且|a|>|b|=-a+2[a+b]-3b+3a=-a+2a+2b-3b+3a=(-a+2a+3a)+(2b-3b)=4a-b3.当x=1时, 则当x=-1时,解:将x=1代入 中得:
a+b-2=3
∴ a+b=5;
当x=-1时
=-a-b-2
=-(a+b)-2
=-7 =-5-2解:原式====5.如果关于x的多项式 的值与x
无关,则a的取值为_____.解:原式=由题意知,则:6a-6=0∴a=116.如果关于x,y的多项式 的差
不含有二次项,求 的值。解:原式=由题意知,则: m-3=0
2+2n=0∴m=3,n=-1;∴ = = -1一、概念中的易错题二、运算中的易错题易错点总结:1.单项式的定义例1.下列各式子中,是单项式的有______________(填序号)①、②、④、⑦ 注意:1.单个的字母或数字也是单项式;
2.用加减号把数字或字母连接在一起
的式子不是单项式;
3.只用乘号把数字或字母连接在一起
的式子仍是单项式;
4.当式子中出现分母时,要留意分母里有
没有字母,有字母的就不是单项式,如
果分母没有字母的仍有可能是单项式
(注:“π”当作数字,而不是字母)2.单项式的系数与次数例2 指出下列单项式的系数和次数;注意:1.字母的系数“1” 可以省略的,但不代表没有系
数(次数也是同样道理);
2.有分母的单项式,分母中的数字也是单项式系
数的一部分;
3.注意“π”不是字母,而是数字,属于系数的一
部分;
4.计算次数的时候并不是简单的见到指数就相
加,注意单项式的次数指的是字母的指数和;3.多项式的项数与次数例3 下列多项式次数为3的是( )C例4 请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项;注意(1)多项式的次数不是所有项的次数的和,而是它的最高
次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次, “π”当作数字,而不是字母4.书写格式中的易错点例5 下列各个式子中,书写格式正确的是( )1.代数式中用到乘法时,若是数字与数字乘,要用“×”
若是数字与字母乘,乘号通常写成”.”或省略不写,如
3×y应写成3·y或3y,且数字与字母相乘时,字母与
字母相乘,乘号通常写成“·”或省略不写。
2.带分数与字母相乘,要写成假分数
3.代数式中出现除法运算时,一般用分数写,即用分数
线代替除号。
4.系数一般写在字母的前面,且系数“1”往往会省略;F例6 王强班上有男生m人,女生比男生的一半多5人,王强班上的总人数(用m表示)为______人。易错点:结果不进行化简,直接写点拨:结果中有 它们是同类项,应合并以保证最后的结果最简.正确的写法是二、运算过程中的易错题1.同类项的判定与合并同类项的法则:例1 判断下列各式是否是同类项?点拨:对于(1)、(3),考察的是同类项的定义,所含字母相同,相同字母的指数也相同的称为同类项;所以(1)、(3)不是同类项;
对于(2),虽然好像它们的次数不一样,但其实它们都是常数项,所以,它们都是同类项;
对于(4),虽然它们的系数不同,字母的顺序也不同,但它依然满足同类项的定义,是同类项;答:(2)、(4)是同类项,(1)(3)不是同类项;例2 下列合并同类项的结果错误的有_______________.①、②、③、④、⑤注意:1,合并同类项的法则是把同类项的系数相加,字母和字母的次数不变;
2,合并同类项后也要注意书写格式;
3,如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;0例3 合并同类项:小明的解法:(1)错在把所有项都当作同类项了;正确的解法:例3 合并同类项:小明的解法:(2)错在把结合同类项时弄错了符号;正确的解法:总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的。2.去括号中的易错题: 判断下列各式是否正确:√××( )( )( )×( )去括号时,1.注意括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2.注意外面有系数的,各项都要乘以那个系数;练一练: 化简下列各式:整式的加减一般步骤是(1)如果有括号就先去括号,
(2)然后再合并同类项.3.化简求值中的易错题:(先去括号)(降幂排列)(合并同类项,化简完成)当x=-2时(代入)(代入时注意添上括号,乘号改回“×”)4.多重括号化简的易错题注意:有多重括号的,一般先去小括号,再去中括号,最后再去大括号;1.去掉下列各式中的括号。(1)8m-(3n+5)(2)n-4(3-2m)(3)2(a-2b)-3(2m-n)=8m-3n-5=n-12+8m=2a-4b-6m+3n2.化简:-(3x-2y+z)-[5x-x+2y-z-3x]解:原式=-(3x-2y+z)-[5x-(x-2y+z)-3x]=-(3x-2y+z)-[x+2y-z]=-(3x-2y+z)-[(5x-x-3x)+2y-z]=-3x+2y-z-x-2y+z=(-3x-x)+(2y-2y)+(-z+z)=-4x练一练:5.“A+2B”类型的易错题:例1 若多项式 计算多项式A-2B;注意:列式时要先加上括号,再去括号;例2 一个多项式A加上 得 ,求这个多项式A?注意:我们在移项的时候是整体移项,不要漏了添上括号;6.实际问题中的易错题:例1 某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在再次下调20%,使收费标准为n元/分钟,那么原收费标准为 ( ).B点拨:为了弄清各数之间的关系,我们可以借助方程来求解.假设原收费标准为每分钟x元,可得:
解得 .应选B.例2 若长方形的一边长为a+2b,另一边长比它的3倍少a-b,求这个长方形的周长?分析:如果直接列式的话,非常麻烦,我们可以先求出另一边长,再求周长,这样就比较容易求出答案;解:一边长为:a+2b;
另一边长为:3(a+2b)-(a-b)
=3a+6b-a+b
=3a-a+6b+b
=2a+7b;
周长为:2(a+2b+2a+7b)
=2(a+2a+2b+7b)
=2(3a+9b)
=6a+18b;答:长方形的周长为6a+18b计算与求值:作业:实际问题(1)小明在实践课中做一个长方形模型,一边为3a+2b,另一边比它小a-b,则长方形的周长为多少?(2)大众超市出售一种商品其原价为a元,现三种调价方案: 1.先提价格上涨20%,再降价格20%
2. 先降价格上涨20%,再提价格20%
3. 先提价格上涨15%,再降价格15%
问用这三种方案调价结果是否一样?最后是不是都恢复了原价?
的一半。推断第一天剩余的长度_____,第二天剩
余的长度_____…第n天剩余的长度_____米米米4.用字母n表示偶数为________奇数为___________5. a与b的差的平方的 是______ 6. a的立方与b的立方的和的2倍是______2n2n+11._____________________________________ 叫做代数式。用运算符号把数字与字母连接起来的式子2. 运算符号包括_________________加,减,乘,除,乘方判断哪些是代数式代数式的定义注意: 单独一个数或一个字母也是代数式。数字与数字相乘不能省乘号。例如:3×4一、书写含乘法运算的代数式
1.乘号省,要酌情
2.数相乘,不能省
3.数在前,字母后
4.带分数,要化假(a+b)×(m+n)=(a+b)(m+n)t×3常写作3t
(2a+b)×3常写作3(2a+b)二、书写含除法运算的代数式除号变,分数线
当代数式中出现含有字母的除法运算时,结果一般不用“÷”,而应改用分数线,其中被除数作分子,除数作分母。
如ah ÷7=三.书写带有单位名称的代数式
1.遇和差,括号加
如(3a-2b)千克不能写作3a-2b千克;
(t-2) ℃ 不能写作t -2 ℃.
2.是积商,直接放 若代数式是积或商的形式,无需加括号,直接在代数式后写上单位名称即可。
如(1+a%)a米,mn元。1、直接代入求值例1:当x=-2,y=-3时,求代数式 的值。解:当x=-2,y=-3时,2、整体代入求值1.解:2.已知 求代数式 的值。输入x解:如输入x=3,则应先列式为再列式为所以表格中应填653转换机:直接输入求值定义:单项式中的_________。次数:1.当单项式的系数是1或-1时,“1”通常省略不写。单项式:系数:数字或字母的乘积由_________________组成的式子。
单独的______或________也是单项式。单项式中的__________________.数字因数所有字母的指数和一个数一个字母注意的问题:2.当式子分母中出现字母时不是单项式。3.圆周率π是常数,不要看成字母。4.当单项式的系数是带分数时,通常写成假分数。5.单项式的系数应包括它前面的性质符号。6.单项式次数是指所有字母的次数的和,与数字的次数没有关系。7.单独的数字不含字母, 规定它的次数是零次.定义:几个__________.常数项:多项式中_______________.多项式的次数:_________________________.
项: 组成多项式中的_____________.
有几项,就叫做_________.1.在确定多项式的项时,要连同它前面的符号,
2.一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式。
3.在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念。多项式单项式的和每一个单项式几项式不含字母的项多项式中次数最高的项的次数。注意的问题:3、 的项是( ),次数是( ),
的项是( ),次数是( ),是( )次( )项式。2、 的系数是( ),次数是( ), 的系数是
( ),次数是( );1、在式子: 中,哪些是单项式,哪些是多项式?哪些是整式?y2、1-x-5xy2 、-x练 一练:y21-x-5xy2 21、-x、-5xy2 返回同类项的定义:(两相同)合并同类项概念:_________________________.合并同类项法则:2._________________不变。2._________________相同。1.____相同,字母相同的字母的指数也1.______相加减;字母和字母的指数系数同类项注意:几个常数项也是______同类项。(两无关)2.与__________无关。1.与____无关系数 字母的位置把多项式中的同类项合并成一项3、若5x2 y与是 x m yn同类项,则m=( ) n=( )
若5x2 y与 x m yn同的和是单项式, m=( ) n=( )1、下列各组是不是同类项:练一练:(1) 4abc 与 4ab (2) -5 m2 n3 与 2n3 m2(3) -0.3 x2 y 与 y x22、合并下列同类项:(1) 3xy – 4 xy – xy = ( ) (2) -a-a-2a=( ) 不是是是 –2xy –4a 2 12 12.若 与 是同类项,则m+n=___.4.若 ,则m+n-p=______543.若 与 的和是一个单项式,则 =___.-41.下列各式中,是同类项的是:___________① 与 ② 与 ③ 与 ⑤ 与 ⑥-125与③⑤⑥④ 与 整式的加减混合运算步骤(有括号先去括号)1.找同类项,做好标记。
2.利用加法的交换律和结合律把同类项放在一起。
3.利用乘法分配律计算结果。
4.按要求按“升”或“降”幂排列。找般并排 1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
“去括号,看符号。是‘+’号,不变号,是‘-’号,全变号”一:去括号二:计算(按照先小括号,再中括号,最后大括号的顺序)3、多项式 与 的和是 ,它们的差
是 ,多项式 减去一个多项 后是 ,则
这个多项式是 。1、去括号: 1) +(x-3)= 2) -(x-3)=
3)-(x+5y-2)= 4)+(3x-5y+6z)= 练一练:x-3-x+3- x- 5y+2 3x-5y+6z2、计算:(1)x-(-y -z+1)= ( 2 ) m+(-n+q)= ;
( 3 ) a - ( b+c-3)= ; ( 4 ) x+(5-3y)= 。
x-5xy2 -3x+xy2 -5a+4ab32ax+y +z -1m-n+qa-b-c+3x+5-3y-2x-4xy2 4x-6xy2 -7a+4ab34、化简已知,求解:跟踪练习:已知求2、已知1、求:(1)(2)例:两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50千米/时,水流速度是a千米/时。
(1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?解:顺水航速=船速+水速=50+a(千米/时)
顺水航速=船速-水速=50-a(千米/时)
跟踪练习:飞机的无风航速为a千米/时,风速为20千米/时,飞机顺风飞行6小时的行程是多少?飞机逆风飞行3小时的行程是多少?两个行程的相差是多少?(2)2小时后甲船比乙船多航行
2(50+a)-2(50-a)
=100+2a-100+2a
=4a(千米)(1) 2小时后两船相距
2(50+a)+2(50-a)
=100+2a+100-2a
=200(千米)一、填空:
1、a的倒数与b的相反数的差,用代数式表示是______.
2、a、b两数的平方差除a、b两数和的平方,所得商为_______.
3、一个两位数,个位上数字是x,十位上数字是个位数字的两倍,这个两位数是_______.
4、若3x 2m-1 y2与-2xy n-1是同类项,则2m-n= _______.
5、若x+y=6,则2- x-y的值是_______.
6、甲、乙两辆车同时从A、B两地相向而行,甲车速度为v千米/时,乙车速度是甲车的2倍还多2千米,若两车出发后4小时相遇,则A、B两地路程可以表示成__ _____ ;若v=40,则A、B两地路程是_____ 千米.巩固练习二、列代数式:1、已知长方形的宽为(2a-b)cm,长比宽多(a-b)cm,求这个长方形的周长。 3a2b - [2a2b -(2abc - a2c)- 4a2c ] – abc 四、求代数式
3a2b - [2a2b -(2abc - a2c)- 4a2c ] – abc的值,
其中a=-2,b=-3,c=1.三、化简:1.观察一列数:3,8,13,18,23,28,……,
依次规律,在数列中第2004个数是_____.2.下面一组按规律排列的数:2,4,8,16,
……,第2005个数应是_______.10018220053.按规律填数:(1)2,7,12,17,( ),( ),……(2)1,2,4,8,16,( ),( ),……4.观察下列算式:(1)第5个等式是___ ___ ;
(2)第n个等式是_______ _______ .-=4=1×4-=12=3×4-=20=5×4-=28=7×4按规律回答:22273264-=36=9×4-=(2n-1) ×45.如图,在2005年3月的日历上: 任意圈出一竖
列上相邻的三个
数,设中间的一个
数为x,则其余两
个数分别为
. x-7,x+7用火柴棒按下图的方式搭三角形 。③②①练一练⑴填写下表 :⑵照这样的规律搭下去,搭n个 这样的三角形需要多少根火柴棒?4n+159131721做一做:用棋子摆出下列一组图形:⑴摆第1个图形用_____枚棋子,摆第2个图形用_____枚棋子,摆第3个图形用______枚棋子;
⑵按照这种方式摆下去,摆第n个图形用_____枚棋子,摆第100个图形用_______枚棋子。3693n3001.探索规律并填空:
(1) .....
。 思考:(2)计算: .1.求当x= 时,多项式的值。解:原式===把x= 带入 中,得 ∴ 原式=5补充例题:化简下列式子:∴原式=-a-2[-(a+b)]-3(b-a)解:由题意知:a<0,b>0且|a|>|b|=-a+2[a+b]-3b+3a=-a+2a+2b-3b+3a=(-a+2a+3a)+(2b-3b)=4a-b3.当x=1时, 则当x=-1时,解:将x=1代入 中得:
a+b-2=3
∴ a+b=5;
当x=-1时
=-a-b-2
=-(a+b)-2
=-7 =-5-2解:原式====5.如果关于x的多项式 的值与x
无关,则a的取值为_____.解:原式=由题意知,则:6a-6=0∴a=116.如果关于x,y的多项式 的差
不含有二次项,求 的值。解:原式=由题意知,则: m-3=0
2+2n=0∴m=3,n=-1;∴ = = -1一、概念中的易错题二、运算中的易错题易错点总结:1.单项式的定义例1.下列各式子中,是单项式的有______________(填序号)①、②、④、⑦ 注意:1.单个的字母或数字也是单项式;
2.用加减号把数字或字母连接在一起
的式子不是单项式;
3.只用乘号把数字或字母连接在一起
的式子仍是单项式;
4.当式子中出现分母时,要留意分母里有
没有字母,有字母的就不是单项式,如
果分母没有字母的仍有可能是单项式
(注:“π”当作数字,而不是字母)2.单项式的系数与次数例2 指出下列单项式的系数和次数;注意:1.字母的系数“1” 可以省略的,但不代表没有系
数(次数也是同样道理);
2.有分母的单项式,分母中的数字也是单项式系
数的一部分;
3.注意“π”不是字母,而是数字,属于系数的一
部分;
4.计算次数的时候并不是简单的见到指数就相
加,注意单项式的次数指的是字母的指数和;3.多项式的项数与次数例3 下列多项式次数为3的是( )C例4 请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项;注意(1)多项式的次数不是所有项的次数的和,而是它的最高
次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次, “π”当作数字,而不是字母4.书写格式中的易错点例5 下列各个式子中,书写格式正确的是( )1.代数式中用到乘法时,若是数字与数字乘,要用“×”
若是数字与字母乘,乘号通常写成”.”或省略不写,如
3×y应写成3·y或3y,且数字与字母相乘时,字母与
字母相乘,乘号通常写成“·”或省略不写。
2.带分数与字母相乘,要写成假分数
3.代数式中出现除法运算时,一般用分数写,即用分数
线代替除号。
4.系数一般写在字母的前面,且系数“1”往往会省略;F例6 王强班上有男生m人,女生比男生的一半多5人,王强班上的总人数(用m表示)为______人。易错点:结果不进行化简,直接写点拨:结果中有 它们是同类项,应合并以保证最后的结果最简.正确的写法是二、运算过程中的易错题1.同类项的判定与合并同类项的法则:例1 判断下列各式是否是同类项?点拨:对于(1)、(3),考察的是同类项的定义,所含字母相同,相同字母的指数也相同的称为同类项;所以(1)、(3)不是同类项;
对于(2),虽然好像它们的次数不一样,但其实它们都是常数项,所以,它们都是同类项;
对于(4),虽然它们的系数不同,字母的顺序也不同,但它依然满足同类项的定义,是同类项;答:(2)、(4)是同类项,(1)(3)不是同类项;例2 下列合并同类项的结果错误的有_______________.①、②、③、④、⑤注意:1,合并同类项的法则是把同类项的系数相加,字母和字母的次数不变;
2,合并同类项后也要注意书写格式;
3,如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;0例3 合并同类项:小明的解法:(1)错在把所有项都当作同类项了;正确的解法:例3 合并同类项:小明的解法:(2)错在把结合同类项时弄错了符号;正确的解法:总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的。2.去括号中的易错题: 判断下列各式是否正确:√××( )( )( )×( )去括号时,1.注意括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2.注意外面有系数的,各项都要乘以那个系数;练一练: 化简下列各式:整式的加减一般步骤是(1)如果有括号就先去括号,
(2)然后再合并同类项.3.化简求值中的易错题:(先去括号)(降幂排列)(合并同类项,化简完成)当x=-2时(代入)(代入时注意添上括号,乘号改回“×”)4.多重括号化简的易错题注意:有多重括号的,一般先去小括号,再去中括号,最后再去大括号;1.去掉下列各式中的括号。(1)8m-(3n+5)(2)n-4(3-2m)(3)2(a-2b)-3(2m-n)=8m-3n-5=n-12+8m=2a-4b-6m+3n2.化简:-(3x-2y+z)-[5x-x+2y-z-3x]解:原式=-(3x-2y+z)-[5x-(x-2y+z)-3x]=-(3x-2y+z)-[x+2y-z]=-(3x-2y+z)-[(5x-x-3x)+2y-z]=-3x+2y-z-x-2y+z=(-3x-x)+(2y-2y)+(-z+z)=-4x练一练:5.“A+2B”类型的易错题:例1 若多项式 计算多项式A-2B;注意:列式时要先加上括号,再去括号;例2 一个多项式A加上 得 ,求这个多项式A?注意:我们在移项的时候是整体移项,不要漏了添上括号;6.实际问题中的易错题:例1 某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在再次下调20%,使收费标准为n元/分钟,那么原收费标准为 ( ).B点拨:为了弄清各数之间的关系,我们可以借助方程来求解.假设原收费标准为每分钟x元,可得:
解得 .应选B.例2 若长方形的一边长为a+2b,另一边长比它的3倍少a-b,求这个长方形的周长?分析:如果直接列式的话,非常麻烦,我们可以先求出另一边长,再求周长,这样就比较容易求出答案;解:一边长为:a+2b;
另一边长为:3(a+2b)-(a-b)
=3a+6b-a+b
=3a-a+6b+b
=2a+7b;
周长为:2(a+2b+2a+7b)
=2(a+2a+2b+7b)
=2(3a+9b)
=6a+18b;答:长方形的周长为6a+18b计算与求值:作业:实际问题(1)小明在实践课中做一个长方形模型,一边为3a+2b,另一边比它小a-b,则长方形的周长为多少?(2)大众超市出售一种商品其原价为a元,现三种调价方案: 1.先提价格上涨20%,再降价格20%
2. 先降价格上涨20%,再提价格20%
3. 先提价格上涨15%,再降价格15%
问用这三种方案调价结果是否一样?最后是不是都恢复了原价?
