第1章反比例函数单元检测题(有答案)湘教版数学九年级上册
文档属性
| 名称 | 第1章反比例函数单元检测题(有答案)湘教版数学九年级上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 545.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-03 19:20:13 | ||
图片预览



文档简介
第1章 单元检测题(后附答案)
(时间:100分钟 满分:120分)
一、选择题(本题共12小题,每题3分,共36分)
1.下列函数中,y与x不是反比例函数的是( )
A.y=- B.y= C.y= D.3xy=2
2.反比例函数y=(k>0)的大致图象是( )
3.函数y=的图象经过( )
A.(2,1) B.(1,1) C.(-1,2) D.(2,2)
4.已知反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
eq \o(\s\up7(),\s\do5(第4题图)) eq \o(\s\up7(),\s\do5(第5题图))
第9题图 eq \o(\s\up7(),\s\do5(第11题图))
5.反比例函数y=-(x<0)的图象如图所示,随着x值的增大,y值( )
A.不变 B.减小 C.增大 D.先减小后增大
6.一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
7.已知正比例函数y=ax的图象与反比例函数y=的图象的一个交点坐标是(1,3),则另一个交点的坐标是( )
A.(-1,-3) B.(-3,-1) C.(-1,-2) D.(-2,-3)
8.下列说法正确的是( )
①反比例函数y=中自变量x的取值范围是x≠0;
②点P(-3,2)在反比例函数y=-的图象上;
③反比例函数y=的图象,在每一个象限内,y随x的增大而增大.
A.①② B.①③ C.②③ D.①②③
9.在同一平面直角坐标系中,一次函数y1=k1x+b与反比例函数y2=(x>0)的图象如图所示,当y1>y2时,自变量x的取值范围为( )
A.x<1 B.x>3 C.0<x<1 D.1<x<3
10.在同一直角坐标系中,函数y=kx-k与y=(k≠0)的大致图象是( )
A.①② B.②③ C.②④ D.③④
11.如图,点A是反比例函数y=(x>0)上的一点,过点A作AC⊥y轴,垂足为点C,AC交反比例函数y=的图象于点B,点P是x轴上的动点,则△PAB的面积为( )
A.2 B.4 C.6 D.8
12.如图所示,在平面直角坐标系xOy中,点A,B,C为反比例函数y=(k>0)上不同的三点,连接OA,OB,OC,过点A作AD⊥y轴于点D,过点B,C分别作BE,CF垂直x轴于点E,F,OC与BE相交于点M,记△AOD,△BOM,四边形CMEF的面积分别为S1,S2,S3,则( )
A.S1=S2+S3 B.S2=S3 C.S3>S2>S1 D.S1S2<S32
二、填空题(本大题共6小题,每小题3分,共18分)
13.反比例函数y=的图象经过点P(-2,3),则k=__ __.
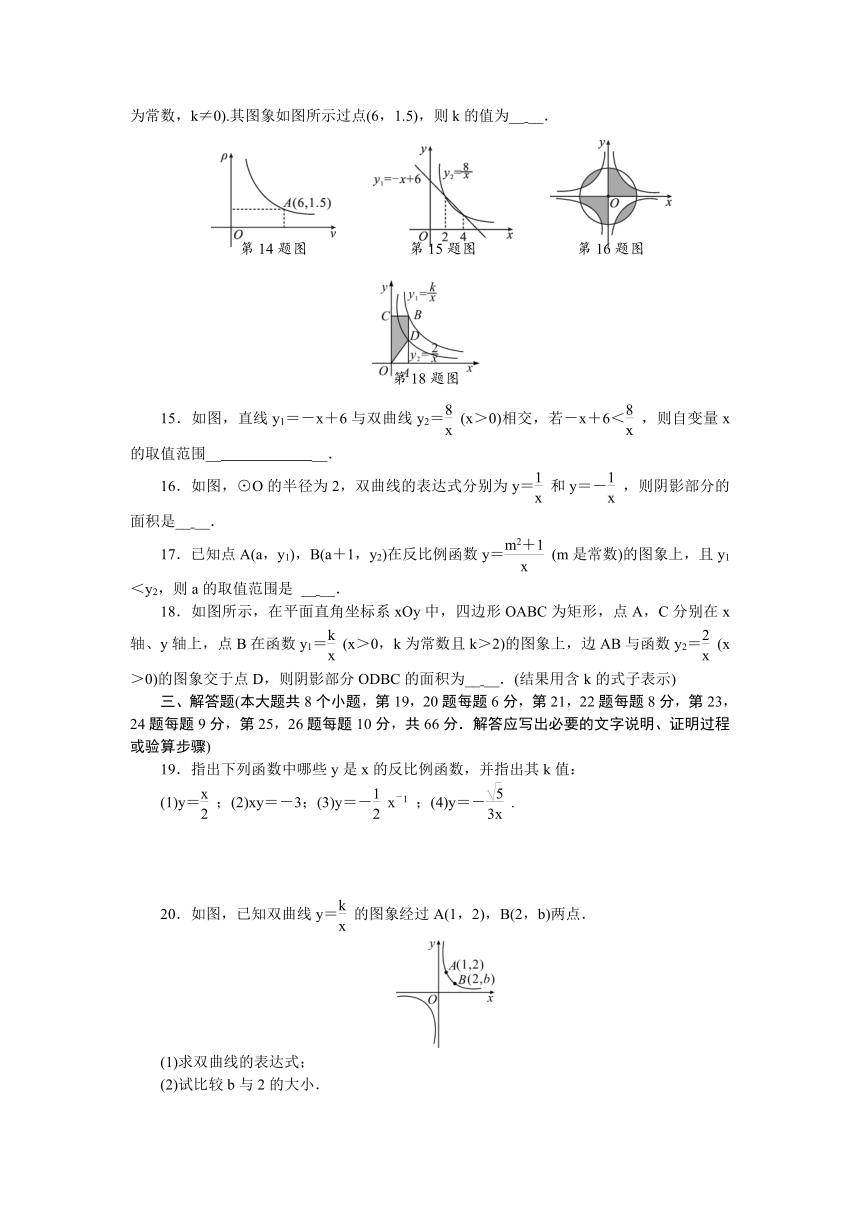
14.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)与体积v(单位:m3)满足函数关系式ρ=(k为常数,k≠0).其图象如图所示过点(6,1.5),则k的值为__ __.
eq \o(\s\up7(),\s\do5(第14题图)) eq \o(\s\up7(),\s\do5(第15题图)) eq \o(\s\up7(),\s\do5(第16题图)) eq \o(\s\up7(),\s\do5(第18题图))
15.如图,直线y1=-x+6与双曲线y2=(x>0)相交,若-x+6<,则自变量x的取值范围__ __.
16.如图,⊙O的半径为2,双曲线的表达式分别为y=和y=-,则阴影部分的面积是__ __.
17.已知点A(a,y1),B(a+1,y2)在反比例函数y=(m是常数)的图象上,且y1<y2,则a的取值范围是 __ __.
18.如图所示,在平面直角坐标系xOy中,四边形OABC为矩形,点A,C分别在x轴、y轴上,点B在函数y1=(x>0,k为常数且k>2)的图象上,边AB与函数y2=(x>0)的图象交于点D,则阴影部分ODBC的面积为__ __.(结果用含k的式子表示)
三、解答题(本大题共8个小题,第19,20题每题6分,第21,22题每题8分,第23,24题每题9分,第25,26题每题10分,共66分.解答应写出必要的文字说明、证明过程或验算步骤)
19.指出下列函数中哪些y是x的反比例函数,并指出其k值:
(1)y=;(2)xy=-3;(3)y=-x-1 ;(4)y=-.
20.如图,已知双曲线y=的图象经过A(1,2),B(2,b)两点.
(1)求双曲线的表达式;
(2)试比较b与2的大小.
21.已知反比例函数y=图象的两个分支分别位于第一、三象限.
(1)求k的取值范围;
(2)取一个你认为符合条件的k值,写出反比例函数的表达式,并求出当x=-6时反比例函数y的值.
22.如图,在平面直角坐标系中,四边形OABC为矩形,点C,A分别在x轴和y轴的正半轴上,点D为AB的中点.已知实数k≠0,一次函数y=-3x+k的图象经过点C,D,反比例函数y=(x>0)的图象经过点B,求k的值.
23.如图,在平面直角坐标系中,一次函数y=x-2的图象与y轴相交于点A,与反比例函数y=在第一象限内的图象相交于点B(m,2),过点B作BC⊥y轴于点C.
(1)求反比例函数的表达式;
(2)求△ABC的面积.
24.阅读下面的材料:
如果函数y=f(x)满足:对于自变量x取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)=x2(x>0)是增函数.
证明:任取x1<x2,且x1>0,x2>0.
则f(x1)-f(x2)=x12-x22=(x1+x2)(x1-x2).
∵x1<x2且x1>0,x2>0,
∴x1+x2>0,x1-x2<0.
∴(x1+x2)(x1-x2)<0,即f(x1)-f(x2)<0,f(x1)<f(x2).
∴函数f(x)=x2(x>0)是增函数.
根据以上材料解答下列问题:
(1)函数f(x)=(x>0),f(1)==1,f(2)=,
f(3)=________,f(4)=________;
(2)猜想f(x)=(x>0)是 ________函数(填“增”或“减”),并证明你的猜想.
25.如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=相交于A(-2,3),B(m,-2)两点.
(1)求y1,y2对应的函数表达式;
(2)过点B作BP∥x轴交y轴于点P,求△ABP的面积;
(3)根据函数图象,直接写出关于x的不等式k1x+b<的解集.
26.电子体重秤读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻R1,R1与踏板上人的质量m之间的函数关系式为R1=km+b(其中k,b为常数,0≤m≤120),其图象如图1所示;图2的电路中,电源电压恒为8伏,定值电阻R0的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为U0,该读数可以换算为人的质量m,
温馨提示:①导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式I=;②串联电路中电流处处相等,各电阻两端的电压之和等于总电压.
(1)求k,b的值;
(2)求R1关于U0的函数表达式;
(3)用含U0的代数式表示m;
(4)若电压表量程为0~6伏,为保护电压表,请确定该电子体重秤可称的最大质量.
答案:
第1章 单元检测题
(时间:100分钟 满分:120分)
1.( C )
2.( A )
3.( A )
4.( C )
5.( C )
6.( A )
7.( A )
8.( A )
9.( D )
10.( B )
11.( A )
12.( B )
13.则k=__-5__.
14.则k的值为__9__.
15.__0<x<2或x>4__.
16.__2π__.
17. __-1<a<0__.
18.__k-1__.
19.
(1)y=;(2)xy=-3;(3)y=-x-1 ;(4)y=-.
解:(1)y不是x的反比例函数 (2)由xy=-3得到:y=-,y是x的反比例函数,k=-3 (3)y是x的反比例函数,k=- (4)y是x的反比例函数,k=-
20.
(1)求双曲线的表达式;
(2)试比较b与2的大小.
解:(1)因为点A(1,2)在函数y=上,所以2=,即k=2,所以双曲线的表达式为y= (2)由函数y=的性质可知在第一象限,y随x的增大而减小,因为2>1,所以b<2
21.
解:(1)∵反比例函数图象分别位于第一、三象限,∴k-1>0,解得k>1
(2)∵k>1,∴若取k=2,则反比例函数的表达式为y=,把x=-6代入,得y=-
22.
解:把y=0代入y=-3x+k,得x=,∴C(,0),.∵BC⊥x轴,∴点B的横坐标为,把x=代入y=,得y=3,∴B(,3),∵点D为AB的中点,∴D(,3),∵点D在直线y=-3x+k上,∴3=-3×+k,∴k=6
23.
解:(1)把B(m,2)代入一次函数y=x-2中,得m-2=2,∴m=3,∴B(3,2),把B(3,2)代入反比例函数y=中,得k=6,∴反比例函数的表达式为y= (2)∵BC⊥y轴,∴C(0,2),BC∥x轴,∴BC=3,令x=0,则y=x-2=-2,∴A(0,-2),∴AC=4,∴S△ABC=AC·BC=6,∴△ABC的面积为6
24.
解:(1)f(3)=,f(4)=,故答案为:, (2)猜想:f(x)=(x>0)是减函数,证明:任取x1<x2,x1>0,x2>0,则f(x1)-f(x2)=-=,∵x1<x2且x1>0,x2>0,∴x2-x1>0,x1x2>0,∴>0,即f(x1)-f(x2)>0,f(x1)>f(x2),∴函数f(x)=(x>0)是减函数
25.
解:(1)把A(-2,3)代入y2=中,得3=,解得k2=-6,∴双曲线的表达式为:y2=-,∴把B(m,-2)代入y2=-,得-2=,解得m=3,∴B(3,-2),把A(-2,3)和B(3,-2)代入y1=k1x+b中,得解得∴直线AB的表达式为:y1=-x+1
(2)过点A作AD⊥BP,交BP的延长线于点D,如图,∵BP∥x轴,∴AD⊥x轴,BP⊥y轴,∵A(-2,3),B(3,-2),∴BP=3,AD=3-(-2)=5,∴S△ABP=BP·AD=×3×5=
(3)由函数图象可知,不等式k1x+b<的解集为:-2<x<0或x>3
26.
解:(1)将(0,240),(120,0)代入R1=km+b,得解得 (2)由题意得:可变电阻两端的电压=电源电压-电表电压,即可变电阻电压=8-U0,∵I=,可变电阻和定值电阻的电流大小相等,∴=.化简得:R1=R0(-1),∵R0=30,∴R1=-30 (3)由(1)可得R1=-2m+240(0≤m≤120),将R1=-2m+240代入R1=-30,得-2m+240=-30,化简得m=-+135(0≤m≤120) (4)∵m=-+135,令y=-,则m=y+135,m随y的增大而增大,而y=-中,∵0≤U0≤6,∴y随U0的增大而增大,∴m随U0的增大而增大,∴U0取最大值6的时候,mmax=-+135=115,∴电子体重秤可称的最大质量为115千克
(时间:100分钟 满分:120分)
一、选择题(本题共12小题,每题3分,共36分)
1.下列函数中,y与x不是反比例函数的是( )
A.y=- B.y= C.y= D.3xy=2
2.反比例函数y=(k>0)的大致图象是( )
3.函数y=的图象经过( )
A.(2,1) B.(1,1) C.(-1,2) D.(2,2)
4.已知反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
eq \o(\s\up7(),\s\do5(第4题图)) eq \o(\s\up7(),\s\do5(第5题图))
第9题图 eq \o(\s\up7(),\s\do5(第11题图))
5.反比例函数y=-(x<0)的图象如图所示,随着x值的增大,y值( )
A.不变 B.减小 C.增大 D.先减小后增大
6.一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
7.已知正比例函数y=ax的图象与反比例函数y=的图象的一个交点坐标是(1,3),则另一个交点的坐标是( )
A.(-1,-3) B.(-3,-1) C.(-1,-2) D.(-2,-3)
8.下列说法正确的是( )
①反比例函数y=中自变量x的取值范围是x≠0;
②点P(-3,2)在反比例函数y=-的图象上;
③反比例函数y=的图象,在每一个象限内,y随x的增大而增大.
A.①② B.①③ C.②③ D.①②③
9.在同一平面直角坐标系中,一次函数y1=k1x+b与反比例函数y2=(x>0)的图象如图所示,当y1>y2时,自变量x的取值范围为( )
A.x<1 B.x>3 C.0<x<1 D.1<x<3
10.在同一直角坐标系中,函数y=kx-k与y=(k≠0)的大致图象是( )
A.①② B.②③ C.②④ D.③④
11.如图,点A是反比例函数y=(x>0)上的一点,过点A作AC⊥y轴,垂足为点C,AC交反比例函数y=的图象于点B,点P是x轴上的动点,则△PAB的面积为( )
A.2 B.4 C.6 D.8
12.如图所示,在平面直角坐标系xOy中,点A,B,C为反比例函数y=(k>0)上不同的三点,连接OA,OB,OC,过点A作AD⊥y轴于点D,过点B,C分别作BE,CF垂直x轴于点E,F,OC与BE相交于点M,记△AOD,△BOM,四边形CMEF的面积分别为S1,S2,S3,则( )
A.S1=S2+S3 B.S2=S3 C.S3>S2>S1 D.S1S2<S32
二、填空题(本大题共6小题,每小题3分,共18分)
13.反比例函数y=的图象经过点P(-2,3),则k=__ __.
14.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)与体积v(单位:m3)满足函数关系式ρ=(k为常数,k≠0).其图象如图所示过点(6,1.5),则k的值为__ __.
eq \o(\s\up7(),\s\do5(第14题图)) eq \o(\s\up7(),\s\do5(第15题图)) eq \o(\s\up7(),\s\do5(第16题图)) eq \o(\s\up7(),\s\do5(第18题图))
15.如图,直线y1=-x+6与双曲线y2=(x>0)相交,若-x+6<,则自变量x的取值范围__ __.
16.如图,⊙O的半径为2,双曲线的表达式分别为y=和y=-,则阴影部分的面积是__ __.
17.已知点A(a,y1),B(a+1,y2)在反比例函数y=(m是常数)的图象上,且y1<y2,则a的取值范围是 __ __.
18.如图所示,在平面直角坐标系xOy中,四边形OABC为矩形,点A,C分别在x轴、y轴上,点B在函数y1=(x>0,k为常数且k>2)的图象上,边AB与函数y2=(x>0)的图象交于点D,则阴影部分ODBC的面积为__ __.(结果用含k的式子表示)
三、解答题(本大题共8个小题,第19,20题每题6分,第21,22题每题8分,第23,24题每题9分,第25,26题每题10分,共66分.解答应写出必要的文字说明、证明过程或验算步骤)
19.指出下列函数中哪些y是x的反比例函数,并指出其k值:
(1)y=;(2)xy=-3;(3)y=-x-1 ;(4)y=-.
20.如图,已知双曲线y=的图象经过A(1,2),B(2,b)两点.
(1)求双曲线的表达式;
(2)试比较b与2的大小.
21.已知反比例函数y=图象的两个分支分别位于第一、三象限.
(1)求k的取值范围;
(2)取一个你认为符合条件的k值,写出反比例函数的表达式,并求出当x=-6时反比例函数y的值.
22.如图,在平面直角坐标系中,四边形OABC为矩形,点C,A分别在x轴和y轴的正半轴上,点D为AB的中点.已知实数k≠0,一次函数y=-3x+k的图象经过点C,D,反比例函数y=(x>0)的图象经过点B,求k的值.
23.如图,在平面直角坐标系中,一次函数y=x-2的图象与y轴相交于点A,与反比例函数y=在第一象限内的图象相交于点B(m,2),过点B作BC⊥y轴于点C.
(1)求反比例函数的表达式;
(2)求△ABC的面积.
24.阅读下面的材料:
如果函数y=f(x)满足:对于自变量x取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)=x2(x>0)是增函数.
证明:任取x1<x2,且x1>0,x2>0.
则f(x1)-f(x2)=x12-x22=(x1+x2)(x1-x2).
∵x1<x2且x1>0,x2>0,
∴x1+x2>0,x1-x2<0.
∴(x1+x2)(x1-x2)<0,即f(x1)-f(x2)<0,f(x1)<f(x2).
∴函数f(x)=x2(x>0)是增函数.
根据以上材料解答下列问题:
(1)函数f(x)=(x>0),f(1)==1,f(2)=,
f(3)=________,f(4)=________;
(2)猜想f(x)=(x>0)是 ________函数(填“增”或“减”),并证明你的猜想.
25.如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=相交于A(-2,3),B(m,-2)两点.
(1)求y1,y2对应的函数表达式;
(2)过点B作BP∥x轴交y轴于点P,求△ABP的面积;
(3)根据函数图象,直接写出关于x的不等式k1x+b<的解集.
26.电子体重秤读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻R1,R1与踏板上人的质量m之间的函数关系式为R1=km+b(其中k,b为常数,0≤m≤120),其图象如图1所示;图2的电路中,电源电压恒为8伏,定值电阻R0的阻值为30欧,接通开关,人站上踏板,电压表显示的读数为U0,该读数可以换算为人的质量m,
温馨提示:①导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式I=;②串联电路中电流处处相等,各电阻两端的电压之和等于总电压.
(1)求k,b的值;
(2)求R1关于U0的函数表达式;
(3)用含U0的代数式表示m;
(4)若电压表量程为0~6伏,为保护电压表,请确定该电子体重秤可称的最大质量.
答案:
第1章 单元检测题
(时间:100分钟 满分:120分)
1.( C )
2.( A )
3.( A )
4.( C )
5.( C )
6.( A )
7.( A )
8.( A )
9.( D )
10.( B )
11.( A )
12.( B )
13.则k=__-5__.
14.则k的值为__9__.
15.__0<x<2或x>4__.
16.__2π__.
17. __-1<a<0__.
18.__k-1__.
19.
(1)y=;(2)xy=-3;(3)y=-x-1 ;(4)y=-.
解:(1)y不是x的反比例函数 (2)由xy=-3得到:y=-,y是x的反比例函数,k=-3 (3)y是x的反比例函数,k=- (4)y是x的反比例函数,k=-
20.
(1)求双曲线的表达式;
(2)试比较b与2的大小.
解:(1)因为点A(1,2)在函数y=上,所以2=,即k=2,所以双曲线的表达式为y= (2)由函数y=的性质可知在第一象限,y随x的增大而减小,因为2>1,所以b<2
21.
解:(1)∵反比例函数图象分别位于第一、三象限,∴k-1>0,解得k>1
(2)∵k>1,∴若取k=2,则反比例函数的表达式为y=,把x=-6代入,得y=-
22.
解:把y=0代入y=-3x+k,得x=,∴C(,0),.∵BC⊥x轴,∴点B的横坐标为,把x=代入y=,得y=3,∴B(,3),∵点D为AB的中点,∴D(,3),∵点D在直线y=-3x+k上,∴3=-3×+k,∴k=6
23.
解:(1)把B(m,2)代入一次函数y=x-2中,得m-2=2,∴m=3,∴B(3,2),把B(3,2)代入反比例函数y=中,得k=6,∴反比例函数的表达式为y= (2)∵BC⊥y轴,∴C(0,2),BC∥x轴,∴BC=3,令x=0,则y=x-2=-2,∴A(0,-2),∴AC=4,∴S△ABC=AC·BC=6,∴△ABC的面积为6
24.
解:(1)f(3)=,f(4)=,故答案为:, (2)猜想:f(x)=(x>0)是减函数,证明:任取x1<x2,x1>0,x2>0,则f(x1)-f(x2)=-=,∵x1<x2且x1>0,x2>0,∴x2-x1>0,x1x2>0,∴>0,即f(x1)-f(x2)>0,f(x1)>f(x2),∴函数f(x)=(x>0)是减函数
25.
解:(1)把A(-2,3)代入y2=中,得3=,解得k2=-6,∴双曲线的表达式为:y2=-,∴把B(m,-2)代入y2=-,得-2=,解得m=3,∴B(3,-2),把A(-2,3)和B(3,-2)代入y1=k1x+b中,得解得∴直线AB的表达式为:y1=-x+1
(2)过点A作AD⊥BP,交BP的延长线于点D,如图,∵BP∥x轴,∴AD⊥x轴,BP⊥y轴,∵A(-2,3),B(3,-2),∴BP=3,AD=3-(-2)=5,∴S△ABP=BP·AD=×3×5=
(3)由函数图象可知,不等式k1x+b<的解集为:-2<x<0或x>3
26.
解:(1)将(0,240),(120,0)代入R1=km+b,得解得 (2)由题意得:可变电阻两端的电压=电源电压-电表电压,即可变电阻电压=8-U0,∵I=,可变电阻和定值电阻的电流大小相等,∴=.化简得:R1=R0(-1),∵R0=30,∴R1=-30 (3)由(1)可得R1=-2m+240(0≤m≤120),将R1=-2m+240代入R1=-30,得-2m+240=-30,化简得m=-+135(0≤m≤120) (4)∵m=-+135,令y=-,则m=y+135,m随y的增大而增大,而y=-中,∵0≤U0≤6,∴y随U0的增大而增大,∴m随U0的增大而增大,∴U0取最大值6的时候,mmax=-+135=115,∴电子体重秤可称的最大质量为115千克
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
