第七章平行线的证明检测题(有答案)北师大版数学八年级上册
文档属性
| 名称 | 第七章平行线的证明检测题(有答案)北师大版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 292.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-03 19:28:42 | ||
图片预览


文档简介
第七章检测题(后附答案)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列语句中,是命题的是( )
A.直线AB和CD垂直吗 B.过线段AB的中点C画AB的垂线
C.同旁内角不互补,两直线不平行 D.连接A,B两点
2.如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是( )
A.65° B.60° C.55° D.75°
3.如图,直线m∥n,AC⊥BC于点C,∠1=30°,则∠2的度数为( )
A.140° B.130° C.120° D.110°
4.如图,在△ABC中,点D在AC上,延长BC至点E,连接DE,则下列结论不成立的是( )
A.∠DCE>∠ADB B.∠ADB>∠DBC
C.∠ADB>∠ACB D.∠ADB>∠DEC
5.如图,直线a∥b,将含30°角的直角三角板ABC(∠ABC=30°)按图中位置摆放,若∠1=110°,则∠2的度数为( )
A.30° B.36° C.40° D.50°
6.如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )
A.(2,3) B.(3,3) C.(4,2) D.(5,1)
第6题图 第7题图
第8题图
7.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
证法1:
∵∠A+∠B+∠ACB=180°(三角形内角和定理),
又∵∠ACD+∠ACB=180°(平角定义),
∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).
∴∠ACD=∠A+∠B(等式性质). 证法2:
∵∠A=76°,∠B=59°,且∠ACD=135°(量角器测量所得),
又∵135°=76°+59°(计算所得),
∴∠ACD=∠A+∠B(等量代换).
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
8.如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=40°时,∠DCN的度数为( )
A.40° B.50° C.60° D.80°
9.如图,直线l1∥l2,直线l3交l1于点A,交l2于点B,过点B的直线l4交l1于点C.若∠3=50°,∠1+∠2+∠3=240°,则∠4等于( )
A.80° B.70° C.60° D.50°
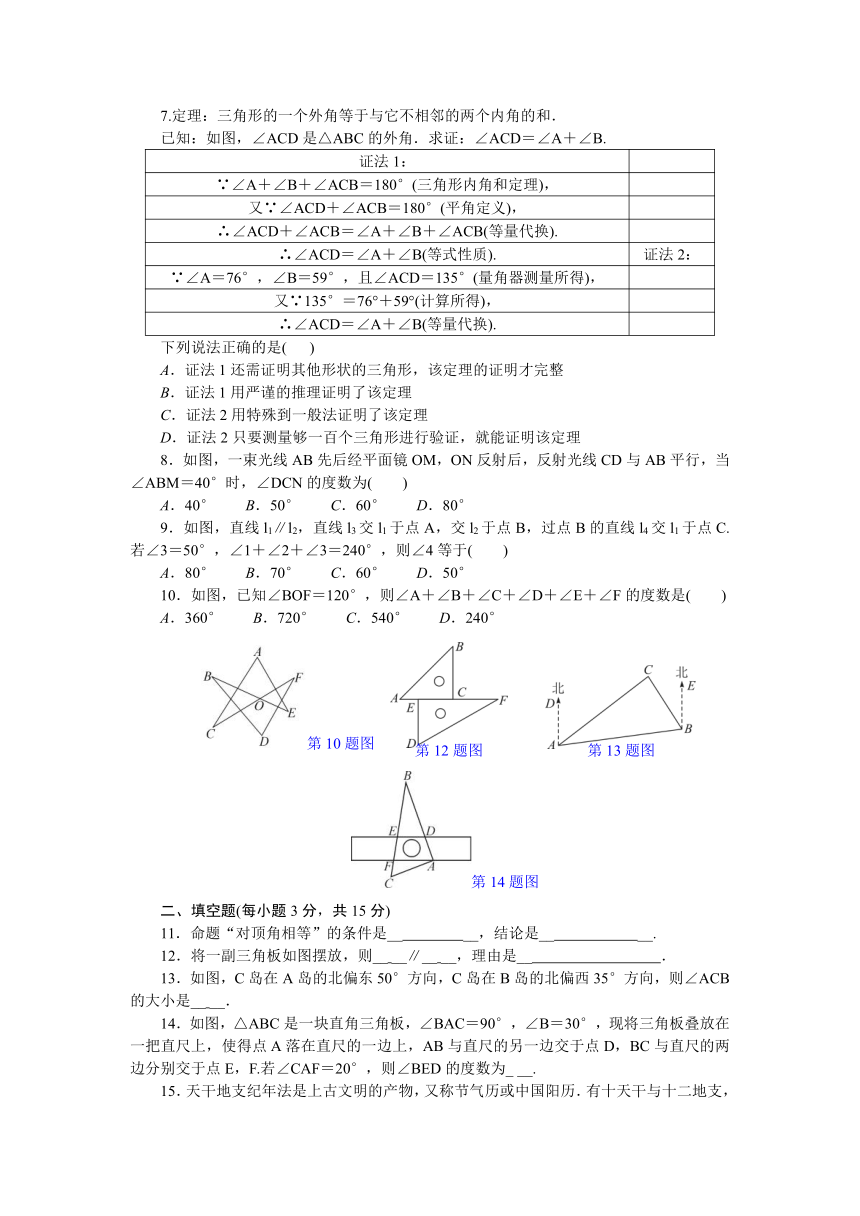
10.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
A.360° B.720° C.540° D.240°
第10题图
第14题图
二、填空题(每小题3分,共15分)
11.命题“对顶角相等”的条件是__ __,结论是__ __.
12.将一副三角板如图摆放,则__ __∥__ __,理由是__ .
13.如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西35°方向,则∠ACB的大小是__ __.
14.如图,△ABC是一块直角三角板,∠BAC=90°,∠B=30°,现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED的度数为_ __.
15.天干地支纪年法是上古文明的产物,又称节气历或中国阳历.有十天干与十二地支,如下表:
天干 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
4 5 6 7 8 9 0 1 2 3
地支 子 丑 寅 卯 辰 巳 午 未 申 酉 戌 亥
4 5 6 7 8 9 10 11 12 1 2 3
算法如下:先用年份的尾数查出天干,再用年份除以12的余数查出地支.如2008年,尾数8为戊,2008除以12余数为4,4为子,那么2008年就是戊子年.
2021年是伟大、光荣、正确的中国共产党成立100周年,则2021年是__ __年.(用天干地支纪年法表示)
三、解答题(共75分)
16.(8分)如图,请完成下列各题:
(1)如果∠1=__ __,那么DE∥AC(__ __);
(2)如果∠1=__ _,那么EF∥BC(__ _);
(3)如果∠FED+__ _=180°,那么AC∥ED(_ __);
(4)如果∠2+__ __=180°,那么AB∥DF(__ __).
17.(9分)一天,爸爸带着小刚到建筑工地去玩,看见有如图所示的人字架,爸爸说:“小刚,我考考你,这个人字架的夹角∠1等于130°,你能求出∠3比∠2大多少吗?”小刚马上得到了正确答案,他的答案是多少?请说明理由.
18.(9分)如图,点A,C,B,D在同一条直线上,BE∥DF,∠A=∠F,AB=FD,求证:AE=FC.
19.(9分)如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F.
20.(9分)如图,BCE,AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,问AD与BE平行吗?说说你的理由.
21.(10分)如图,△ABC中,D为BC上一点,∠C=∠BAD,△ABC的角平分线BE交AD于点F.
(1)求证:∠AEF=∠AFE;
(2)G为BC上一点,当FE平分∠AFG且∠C=30°时,求∠CGF的度数.
22.(10分)如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得△AED,AE与BC交于点F.
(1)填空:∠AFC=__ _度;
(2)求∠EDF的度数.
23.(11分)问题1:
如图①,一张三角形纸片ABC,点D,E分别是△ABC边上的两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是__ _;
研究(2):如果折成图②的形状,猜想∠BDA′,∠CEA′和∠A的数量关系是__ _;
研究(3):如果折成图③的形状,猜想∠BDA′,∠CEA′和∠A的数量关系,并说明理由.
问题2:
研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A,B落在四边形EFCD的内部时,∠1+∠2与∠A,∠B之间的数量关系是__ __.
答案;
第七章检测题
(时间:100分钟 满分:120分)
1.( C )
2.( C )
3.( C )
4.( A )
5.( C )
6.( C )
7.( B )
8.( B )
9.( B )
10.( D )
11.__两个角是对顶角__,结论是__这两个角相等__.
12.则__BC__∥__ED__,__内错角相等,两直线平行__.
13.__85°__.
14.__80°__.
15._辛丑__
16.
(1)如果∠1=__∠C__,那么DE∥AC(__同位角相等,两直线平行__);
(2)如果∠1=__∠FED__,那么EF∥BC(__内错角相等,两直线平行__);
(3)如果∠FED+__∠EFC__=180°,那么AC∥ED(__同旁内角互补,两直线平行__);
(4)如果∠2+__∠AED__=180°,那么AB∥DF(__同旁内角互补,两直线平行__).
17.
解:50°,因为∠1=130°,所以与∠1相邻的内角为50°,所以∠3-∠2=50°
18.
证明:∵BE∥DF,∴∠ABE=∠D,又∵AB=FD,∠A=∠F,∴△ABE≌△FDC(ASA),∴AE=FC
19.
证明:∵CE∥DF,∴∠ACE=∠D,∵∠A=∠1,∴180°-∠ACE-∠A=180°-∠D-∠1,又∵∠E=180°-∠ACE-∠A,∠F=180°-∠D-∠1,∴∠E=∠F
20.
解:AD∥BE.理由:∵AB∥CD,∴∠1=∠ACD,∵∠3=∠E+∠CAF,∠4=∠ACD+∠CAF,∠3=∠4,∴∠1=∠E=∠ACD,∵∠1=∠2,∴∠2=∠E,∴AD∥BE
21.
解:(1)∵BE平分∠ABC,∴∠ABE=∠CBE,∵∠AFE=∠ABF+∠BAD,∠AEF=∠CBE+∠C,∠BAD=∠C,∴∠AEF=∠AFE
(2)∵FE平分∠AFG,∴∠AFE=∠GFE,∵∠AEF=∠AFE,∴∠AEF=∠GFE,∴FG∥AC,∵∠C=30°,∴∠CGF=180°-∠C=150°
22.
(1)填空:∠AFC=__110__度;
(2)求∠EDF的度数.
解:(2)∵∠B=50°,∠BAD=30°,∴∠ADB=180°-50°-30°=100°,∵△ABD沿AD折叠得到△AED,∴∠ADE=∠ADB=100°,∴∠EDF=∠EDA+∠BDA-∠BDF=100°+100°-180°=20°
23.(11分)问题1:
如图①,一张三角形纸片ABC,点D,E分别是△ABC边上的两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是__∠BDA′=2∠A__;
研究(2):如果折成图②的形状,猜想∠BDA′,∠CEA′和∠A的数量关系是__∠BDA′+∠CEA′=2∠A__;
研究(3):如果折成图③的形状,猜想∠BDA′,∠CEA′和∠A的数量关系,并说明理由.
问题2:
研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A,B落在四边形EFCD的内部时,∠1+∠2与∠A,∠B之间的数量关系是__∠1+∠2=2(∠A+∠B)-360°__.
解:研究(1):根据折叠的性质可知∠DA′E=∠A,∠DA′E+∠A=∠BDA′,所以∠BDA′=2∠A.故答案为:∠BDA′=2∠A
研究(2):由图形折叠的性质可知,∠CEA′=180°-2∠DEA′①,∠BDA′=180°-2∠A′DE②,①+②,得∠BDA′+∠CEA′=360°-2(∠DEA′+∠A′DE),即∠BDA′+∠CEA′=360°-2(180°-∠A),所以∠BDA′+∠CEA′=2∠A.故答案为:∠BDA′+∠CEA′=2∠A
研究(3):∠BDA′-∠CEA′=2∠A.证明如下:连接AA′,图略,易知∠DA′A=∠DAA′,∠EA′A=∠EAA′,∴∠BDA′=2∠DA′A,∠CEA′=2∠EA′A,得∠BDA′-∠CEA′=2∠A
研究(4):由图形折叠的性质可知∠1=180°-2∠AEF,∠2=180°-2∠BFE,两式相加得,∠1+∠2=360°-2(∠AEF+∠BFE),即∠1+∠2=360°-2(360°-∠A-∠B),∴∠1+∠2=2(∠A+∠B)-360°.故答案为:∠1+∠2=2(∠A+∠B)-360°
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列语句中,是命题的是( )
A.直线AB和CD垂直吗 B.过线段AB的中点C画AB的垂线
C.同旁内角不互补,两直线不平行 D.连接A,B两点
2.如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是( )
A.65° B.60° C.55° D.75°
3.如图,直线m∥n,AC⊥BC于点C,∠1=30°,则∠2的度数为( )
A.140° B.130° C.120° D.110°
4.如图,在△ABC中,点D在AC上,延长BC至点E,连接DE,则下列结论不成立的是( )
A.∠DCE>∠ADB B.∠ADB>∠DBC
C.∠ADB>∠ACB D.∠ADB>∠DEC
5.如图,直线a∥b,将含30°角的直角三角板ABC(∠ABC=30°)按图中位置摆放,若∠1=110°,则∠2的度数为( )
A.30° B.36° C.40° D.50°
6.如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )
A.(2,3) B.(3,3) C.(4,2) D.(5,1)
第6题图 第7题图
第8题图
7.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
证法1:
∵∠A+∠B+∠ACB=180°(三角形内角和定理),
又∵∠ACD+∠ACB=180°(平角定义),
∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).
∴∠ACD=∠A+∠B(等式性质). 证法2:
∵∠A=76°,∠B=59°,且∠ACD=135°(量角器测量所得),
又∵135°=76°+59°(计算所得),
∴∠ACD=∠A+∠B(等量代换).
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
8.如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=40°时,∠DCN的度数为( )
A.40° B.50° C.60° D.80°
9.如图,直线l1∥l2,直线l3交l1于点A,交l2于点B,过点B的直线l4交l1于点C.若∠3=50°,∠1+∠2+∠3=240°,则∠4等于( )
A.80° B.70° C.60° D.50°
10.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
A.360° B.720° C.540° D.240°
第10题图
第14题图
二、填空题(每小题3分,共15分)
11.命题“对顶角相等”的条件是__ __,结论是__ __.
12.将一副三角板如图摆放,则__ __∥__ __,理由是__ .
13.如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西35°方向,则∠ACB的大小是__ __.
14.如图,△ABC是一块直角三角板,∠BAC=90°,∠B=30°,现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED的度数为_ __.
15.天干地支纪年法是上古文明的产物,又称节气历或中国阳历.有十天干与十二地支,如下表:
天干 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
4 5 6 7 8 9 0 1 2 3
地支 子 丑 寅 卯 辰 巳 午 未 申 酉 戌 亥
4 5 6 7 8 9 10 11 12 1 2 3
算法如下:先用年份的尾数查出天干,再用年份除以12的余数查出地支.如2008年,尾数8为戊,2008除以12余数为4,4为子,那么2008年就是戊子年.
2021年是伟大、光荣、正确的中国共产党成立100周年,则2021年是__ __年.(用天干地支纪年法表示)
三、解答题(共75分)
16.(8分)如图,请完成下列各题:
(1)如果∠1=__ __,那么DE∥AC(__ __);
(2)如果∠1=__ _,那么EF∥BC(__ _);
(3)如果∠FED+__ _=180°,那么AC∥ED(_ __);
(4)如果∠2+__ __=180°,那么AB∥DF(__ __).
17.(9分)一天,爸爸带着小刚到建筑工地去玩,看见有如图所示的人字架,爸爸说:“小刚,我考考你,这个人字架的夹角∠1等于130°,你能求出∠3比∠2大多少吗?”小刚马上得到了正确答案,他的答案是多少?请说明理由.
18.(9分)如图,点A,C,B,D在同一条直线上,BE∥DF,∠A=∠F,AB=FD,求证:AE=FC.
19.(9分)如图,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F.
20.(9分)如图,BCE,AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,问AD与BE平行吗?说说你的理由.
21.(10分)如图,△ABC中,D为BC上一点,∠C=∠BAD,△ABC的角平分线BE交AD于点F.
(1)求证:∠AEF=∠AFE;
(2)G为BC上一点,当FE平分∠AFG且∠C=30°时,求∠CGF的度数.
22.(10分)如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得△AED,AE与BC交于点F.
(1)填空:∠AFC=__ _度;
(2)求∠EDF的度数.
23.(11分)问题1:
如图①,一张三角形纸片ABC,点D,E分别是△ABC边上的两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是__ _;
研究(2):如果折成图②的形状,猜想∠BDA′,∠CEA′和∠A的数量关系是__ _;
研究(3):如果折成图③的形状,猜想∠BDA′,∠CEA′和∠A的数量关系,并说明理由.
问题2:
研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A,B落在四边形EFCD的内部时,∠1+∠2与∠A,∠B之间的数量关系是__ __.
答案;
第七章检测题
(时间:100分钟 满分:120分)
1.( C )
2.( C )
3.( C )
4.( A )
5.( C )
6.( C )
7.( B )
8.( B )
9.( B )
10.( D )
11.__两个角是对顶角__,结论是__这两个角相等__.
12.则__BC__∥__ED__,__内错角相等,两直线平行__.
13.__85°__.
14.__80°__.
15._辛丑__
16.
(1)如果∠1=__∠C__,那么DE∥AC(__同位角相等,两直线平行__);
(2)如果∠1=__∠FED__,那么EF∥BC(__内错角相等,两直线平行__);
(3)如果∠FED+__∠EFC__=180°,那么AC∥ED(__同旁内角互补,两直线平行__);
(4)如果∠2+__∠AED__=180°,那么AB∥DF(__同旁内角互补,两直线平行__).
17.
解:50°,因为∠1=130°,所以与∠1相邻的内角为50°,所以∠3-∠2=50°
18.
证明:∵BE∥DF,∴∠ABE=∠D,又∵AB=FD,∠A=∠F,∴△ABE≌△FDC(ASA),∴AE=FC
19.
证明:∵CE∥DF,∴∠ACE=∠D,∵∠A=∠1,∴180°-∠ACE-∠A=180°-∠D-∠1,又∵∠E=180°-∠ACE-∠A,∠F=180°-∠D-∠1,∴∠E=∠F
20.
解:AD∥BE.理由:∵AB∥CD,∴∠1=∠ACD,∵∠3=∠E+∠CAF,∠4=∠ACD+∠CAF,∠3=∠4,∴∠1=∠E=∠ACD,∵∠1=∠2,∴∠2=∠E,∴AD∥BE
21.
解:(1)∵BE平分∠ABC,∴∠ABE=∠CBE,∵∠AFE=∠ABF+∠BAD,∠AEF=∠CBE+∠C,∠BAD=∠C,∴∠AEF=∠AFE
(2)∵FE平分∠AFG,∴∠AFE=∠GFE,∵∠AEF=∠AFE,∴∠AEF=∠GFE,∴FG∥AC,∵∠C=30°,∴∠CGF=180°-∠C=150°
22.
(1)填空:∠AFC=__110__度;
(2)求∠EDF的度数.
解:(2)∵∠B=50°,∠BAD=30°,∴∠ADB=180°-50°-30°=100°,∵△ABD沿AD折叠得到△AED,∴∠ADE=∠ADB=100°,∴∠EDF=∠EDA+∠BDA-∠BDF=100°+100°-180°=20°
23.(11分)问题1:
如图①,一张三角形纸片ABC,点D,E分别是△ABC边上的两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是__∠BDA′=2∠A__;
研究(2):如果折成图②的形状,猜想∠BDA′,∠CEA′和∠A的数量关系是__∠BDA′+∠CEA′=2∠A__;
研究(3):如果折成图③的形状,猜想∠BDA′,∠CEA′和∠A的数量关系,并说明理由.
问题2:
研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A,B落在四边形EFCD的内部时,∠1+∠2与∠A,∠B之间的数量关系是__∠1+∠2=2(∠A+∠B)-360°__.
解:研究(1):根据折叠的性质可知∠DA′E=∠A,∠DA′E+∠A=∠BDA′,所以∠BDA′=2∠A.故答案为:∠BDA′=2∠A
研究(2):由图形折叠的性质可知,∠CEA′=180°-2∠DEA′①,∠BDA′=180°-2∠A′DE②,①+②,得∠BDA′+∠CEA′=360°-2(∠DEA′+∠A′DE),即∠BDA′+∠CEA′=360°-2(180°-∠A),所以∠BDA′+∠CEA′=2∠A.故答案为:∠BDA′+∠CEA′=2∠A
研究(3):∠BDA′-∠CEA′=2∠A.证明如下:连接AA′,图略,易知∠DA′A=∠DAA′,∠EA′A=∠EAA′,∴∠BDA′=2∠DA′A,∠CEA′=2∠EA′A,得∠BDA′-∠CEA′=2∠A
研究(4):由图形折叠的性质可知∠1=180°-2∠AEF,∠2=180°-2∠BFE,两式相加得,∠1+∠2=360°-2(∠AEF+∠BFE),即∠1+∠2=360°-2(360°-∠A-∠B),∴∠1+∠2=2(∠A+∠B)-360°.故答案为:∠1+∠2=2(∠A+∠B)-360°
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
