2023-2024学年苏科版九年级数学上册4.3等可能条件下的概率(二)同步训练(含解析)
文档属性
| 名称 | 2023-2024学年苏科版九年级数学上册4.3等可能条件下的概率(二)同步训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 303.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-04 00:00:00 | ||
图片预览




文档简介
4.3等可能条件下的概率(二)同步训练-苏科版九年级数学上册
一、选择题
1.某火车站的显示屏每间隔4分钟显示一次火车班次的信息,显示时间持续1分钟,某人到达该车站时,显示屏正好显示火车班次信息的概率是( )
A. B. C. D.
2.如图,四个转盘分别被分成不同的等份.若让转盘自由转动一次,停止后指针落在阴影区域内的概率最大的转盘是( )
A. B.
C. D.
3.从长度分别为2、3、4、5的4条线段中任取3条,能构成钝角三角形的概率为( )
A. B. C. D.
4.南校区学生收到学生捡到的4张校园卡,其中来自初一年级的有1张,初二年级的2张,随机抽取2张校园卡,全部来自初二的年级的概率为( )
A. B. C. D.
5.用如图所示的两个转盘分别进行四等分和三等分,设计一个“配紫色”的游戏,分别转动两个转盘指针指向区域分界线时,忽略不计,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率为( )
A. B. C. D.
6.甲、乙两人各自掷一个普通的正方体骰子,如果两者之和为偶数,甲得1分;如果两者之和为奇数,乙得1分,此游戏( )
A.是公平的 B.对乙有利 C.对甲有利 D.以上都不对
7.如图,是由半圆和长方形拼成一个转盘,其中点O是半圆的圆心,半圆的直径与长方形的宽相等,直径和过点O的长方形长边的平行线,把转盘分成4个部分若任意转动指针,指针停止的位置是等可能的,则指针指向阴影部分的概率是( )
A. B. C. D.因长方形的长没有告知,所以概率不确定
8.如图,正方形 中,点 是以 为直径的半圆与对角线 的交点.现随机向正方形 内投掷一枚小针,则针尖落在阴影区域的概率为( )
A. B. C. D.
9.学生甲手中有4,6,8三张扑克牌,学生乙手中有3,5,10三张扑克牌,现每人从各自手中随机取出一张牌进行比较,数字大者胜,在该游戏中( )
A.甲获胜的概率大 B.乙获胜的概率大
C.两人获胜概率一样大 D.不能确定
10.下列游戏对双方公平的是( )
A.随意转动被等分成3个扇形,且分别均匀涂有红、黄、绿三种颜色的转盘,若指针指向绿色区域,则小明胜,否则小亮胜
B.从一个装有3个红球,2个黄球和2个黑球(这些球除颜色外完全相同)的袋中任意摸出一个球,若是红球,则小明胜,否则小亮胜
C.投掷一枚均匀的正方体形状的骰子,若偶数点朝上,则小明胜,若是奇数点朝上,则小亮胜
D.从分别标有数1,2,3,4,5的五张纸条中,任意抽取一张,若抽到的纸条所标的数字为偶数,则小明胜,若抽到的纸条所标的数字为奇数,则小亮胜
11.如图,正六边形中,点A在一边上运动,AO交六边形的另一边于B,过O作AB的垂线交六边形于C,D,形成如图所示的阴影部分.小姜设计了两个方案:①把如图所示的飞镖盘纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是.②以O为旋转中心,把六边形做成转盘,则指针落在阴影部分的概率是.那么以上两种方案正确的是( )
A.①② B.① C.② D.①②都错误
12.22届年级组董老师为学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小赵同学同时转动A盘和B盘,她赢得游戏的概率是( )
A. B. C. D.
二、填空题
13.袋中装有一个红球和二个黄球,它们除了颜色外都相同,随机从中摸出一球,记录下颜色后放回袋中,充分摇匀后,再随机摸出一球,两次都摸到红球的概率是 。
14.李老师在墙上挂了一幅如图所示的图案,假设可以在图中随意钉钉子,那么这个钉子钉在阴影部分(边界忽略不计)的概率是 .
15.在四个完全相同的球上分别标上数字1、2、3、4,从这四个球 中随机取出一个球记所标数字为,放回后再随机取出一个球记所标数字为,则的概率为 .
16.已知A,B两组卡片共5张,A中三张分别写有数字2,4,6,B中两张分别写有3,5,它们除数字外没有任何区别.现制定这样一个游戏规则:随机地分别从A,B中各抽取一张,若所选出的两数之积为3的倍数,则甲获胜;否则乙获胜.这样的游戏规则对 有利.
三、解答题
17.在5张相同的小纸条上,分别写有:①;②;③1;④乘法;⑤加法.将这5张小纸条做成5支签,①、②、③放在不透明的盒子A中搅匀,④、⑤放在不透明的盒子B中搅匀.
(1)从盒子中任意抽出支签,抽到无理数的概率是 ;
(2)先从盒子中任意抽出支签,再从盒子中任意抽出支签,求抽到的个实数进行相应的运算后结果是无理数的概率.
18.如图,从一个大正方形中截去面积为3cm 和12cm 的两个小正方形,若随机向大正方形内投一粒米,求米粒落在图中阴影部分的概率.
19.一个不透明的布袋里装有20个除颜色外均相同的小球,其中白球有x个,红球有个,其他均为黄球.现从布袋中随机摸出一个球,若是红球则甲同学获胜,若为黄球,则乙同学获胜.
(1)当时,谁获胜的可能性大?
(2)要使游戏对甲乙双方是公平的,x应取何值?
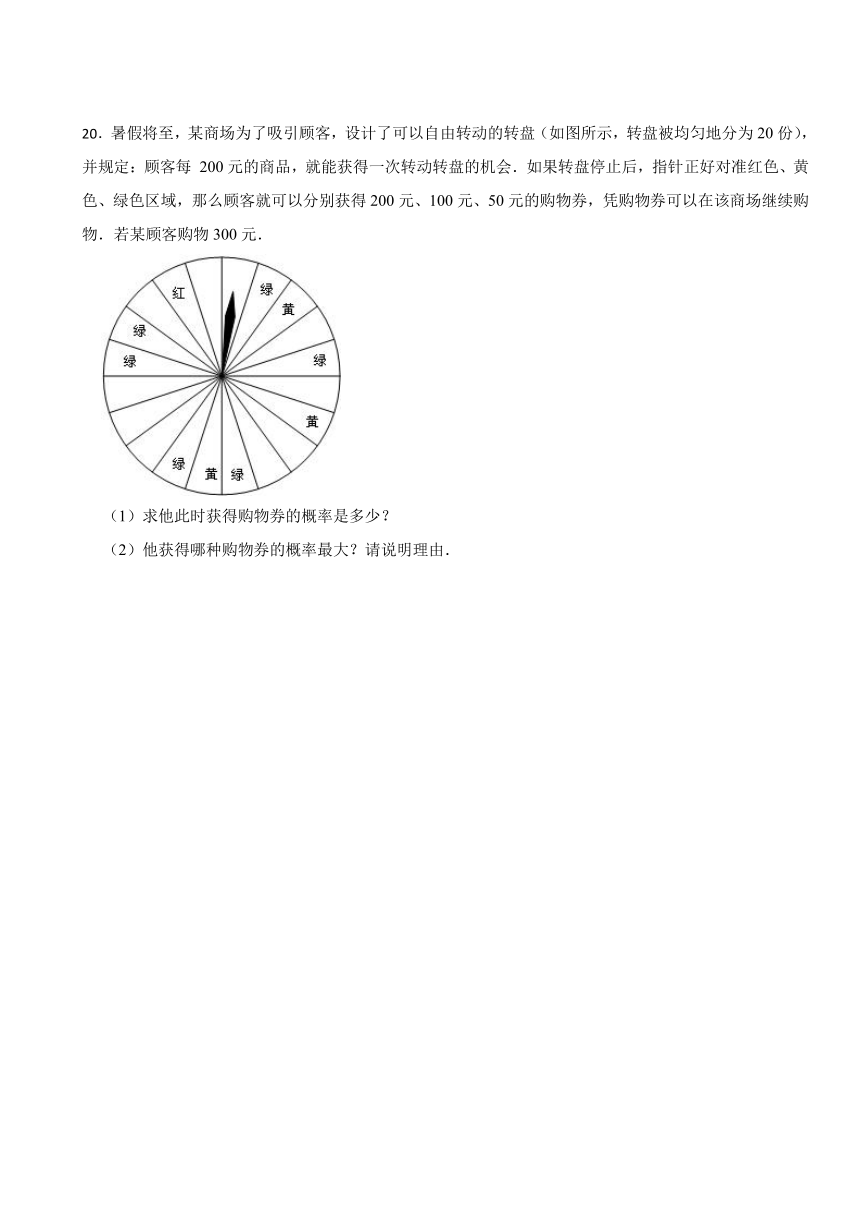
20.暑假将至,某商场为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被均匀地分为20份),并规定:顾客每 200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.若某顾客购物300元.
(1)求他此时获得购物券的概率是多少?
(2)他获得哪种购物券的概率最大?请说明理由.
答案解析部分
1.【答案】B
【解析】解:由于显示屏每间隔4分钟显示一次火车班次的信息,显示时间持续1分钟,
所以显示屏上每隔5分钟就有一分钟的显示时间,
某人到达该车站时正好显示火车班次信息的概率是 .
故答案为:B.
2.【答案】D
【解析】解:A、让转盘自由转动一次,停止后指针落在阴影区域内的概率为;
B、让转盘自由转动一次,停止后指针落在阴影区域内的概率为;
C、让转盘自由转动一次,停止后指针落在阴影区域内的概率为;
D、让转盘自由转动一次,停止后指针落在阴影区域内的概率为;
∵,
∴让转盘自由转动一次,停止后指针落在阴影区域内的概率最大的转盘是选项D的转盘.
故答案为:D.
3.【答案】B
【解析】解:可能的结果有4种:2,3,4;2,3,5;2,4,5;3,4,5.其中,可以构成钝角三角形的有2种情形:2,3,4;2,4,5.∴能组成三角形的概率为= .故答案为:B.
4.【答案】B
【解析】画树状图得:
共有12种等可能性,其中符合条件的有2种,所以P= .
故答案为: B.
5.【答案】A
【解析】解:第一个转盘转出红色的概率为,转出蓝色的概率为,第二个转盘转出红色的概率为,转出蓝色的概率为,然后根据红色与蓝色可配成紫色可得:配成紫色的概率为×+×=.
故答案为:A.
6.【答案】C
【解析】解:甲、乙两人各自掷一个普通的正方体骰子,共有36种结果,其中两者之积为偶数有27种,两者之积为奇数有9种,两者之积为偶数的概率为 ,则两者之积为奇数的概率为 , ,
故答案为:C.
7.【答案】A
【解析】解:转动转盘指针转过的角度为360° ,指针在阴影部分转过的角度为90° ,
转盘停止转动时指针指向阴影部分的概率是: .
故答案为:A.
8.【答案】B
【解析】解:连接BE,如图,
∵AB为直径,
∴∠AEB=90°,
而AC为正方形的对角线,
∴AE=BE=CE,
∴弓形AE的面积=弓形BE的面积,
∴阴影部分的面积=△BCE的面积,
∴镖落在阴影部分的概率= .
故答案为:B.
9.【答案】A
【解析】解:由题意知,甲取出4时,乙有3,5,10共三种可能,其中甲获胜有1种可能;
甲取出6时,乙有3,5,10共三种可能,其中甲获胜有2种可能;
甲取出8时,乙有3,5,10共三种可能,其中甲获胜有2种可能;
∴甲获胜的概率为 ,则乙获胜的概率为
∵
∴甲获胜的概率大
故答案为:A.
10.【答案】C
【解析】解:A中:P(小明胜)=P(小亮胜)=,P(小明胜)<P(小亮胜);不公平
B中:P(小明胜)=P(小亮胜)=,P(小明胜)>P(小亮胜);不公平
C中:P(小明胜)= P(小亮胜)=,P(小明胜)=P(小亮胜);公平
D中:P(小明胜)=P(小亮胜)=,P(小明胜)>P(小亮胜);不公平
故选C.
11.【答案】C
【解析】解:∵共正六边形的中心的直线能将正六边形平分,
∴当AB⊥CD时,两条直线能将正六边形平均分成四份,
∴阴影部分的面积是整个正六边形的面积的,
∴飞镖落在阴影部分和指针指向阴影部分的概率均为,
∴②均正确.
故选C.
12.【答案】C
【解析】解:∵B盘中蓝色扇形区域所占的圆心角为120°,
∴B盘红色扇形区域所占的圆心角为240°,
∴B盘中:S红色扇形=2S蓝色扇形,
画树状图如下:
∴一共有9种等可能的结果,其中一个转盘转出了红色、另一个转盘转出了蓝色的有3种情况,
∴小赵同学同时转动A盘和B盘,她赢得游戏的概率是=.
故答案为:C.
13.【答案】
【解析】解:
红 黄1 黄2
红 红红 黄1红 黄2红
黄1 红黄1 黄1黄1 黄2黄1
黄2 红黄2 黄1黄2 黄2黄2
由表可知两次摸球共有9种等可能结果,其中两次都是红球的只有1种,
∴P(红红)=。
故答案为:
14.【答案】
【解析】解:设阴影部分的面积为 ,则整个图形的面积为 ,
则:P(钉子钉在阴影部分)= .
故答案为:
15.【答案】
【解析】解:a有4种可能,b也有4种可能,
∴共44=16种可能
其中, 的可能有6种情况:
∴其概率为
故答案为:
16.【答案】甲
【解析】画树状图如下:
共有6种等可能的结果,甲获胜的情况有4种,故P(甲获胜) ,
∴这样的游戏规则对甲有利.
17.【答案】(1)
(2)解:树状图画出所有情况为:
即抽签的组合有12种,分别为:
组合情况 运算结果 运算结果是否是无理数
第一种组合 ,,乘法 否
第二种组合 ,,加法 是
第三种组合 ,,乘法 是
第四种组合 ,,加法 是
第五种组合 ,,乘法 否
第六种组合 ,,加法 是
第七种组合 ,,乘法 是
第八种组合 ,,加法 是
第九种组合 ,,乘法 是
第十种组合 ,,加法 是
第十一种组合 ,,乘法; 是
第十二种组合 ,,加法 是
对应的组合运算结果共12个,其中运算结果为无理数的有10个,
故抽到的2个实数进行相应的运算后结果是无理数的概率为.
【解析】解:(1)∵,
∴三个数中,无理数有与两个,
∴ 从盒子A中任意抽出1支签,抽到无理数的概率是;
故答案为:;
18.【答案】解:∵两个空白正方形的面积分别为12 cm 和3 cm ,
∴边长分别为cm和cm,
∴大正方形的边长为cm,
∴大正方形的面积为cm ,
∴阴影部分的面积为27-12-3=12 cm ,
∴米粒落在图中阴影部分的概率.
19.【答案】(1)解:当时,则红球有10个,黄球有5个,
红球的个数多于黄球的个数,
摸到红球的可能性更大,
当时,甲同学获胜可能性大;
(2)解:要使游戏对甲乙双方公平,必须有:
解得;
当时,游戏对甲乙双方是公平的.
20.【答案】(1)解:∵转盘被均匀地分为20份,他此时获得购物券的有10份,
∴他此时获得购物券的概率是:=
(2)解:∵P(获得200元购物券)=,P(获得100元购物券)=,P(获得50元购物券)==,
∴他获得50元购物券的概率最大.
【解析】【分析】(1)根据 转盘被均匀地分为20份,他此时获得购物券的有10份, 求概率即可;
(2)先求出 P(获得200元购物券)=,P(获得100元购物券)=,P(获得50元购物券)==, 再求解即可。
一、选择题
1.某火车站的显示屏每间隔4分钟显示一次火车班次的信息,显示时间持续1分钟,某人到达该车站时,显示屏正好显示火车班次信息的概率是( )
A. B. C. D.
2.如图,四个转盘分别被分成不同的等份.若让转盘自由转动一次,停止后指针落在阴影区域内的概率最大的转盘是( )
A. B.
C. D.
3.从长度分别为2、3、4、5的4条线段中任取3条,能构成钝角三角形的概率为( )
A. B. C. D.
4.南校区学生收到学生捡到的4张校园卡,其中来自初一年级的有1张,初二年级的2张,随机抽取2张校园卡,全部来自初二的年级的概率为( )
A. B. C. D.
5.用如图所示的两个转盘分别进行四等分和三等分,设计一个“配紫色”的游戏,分别转动两个转盘指针指向区域分界线时,忽略不计,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率为( )
A. B. C. D.
6.甲、乙两人各自掷一个普通的正方体骰子,如果两者之和为偶数,甲得1分;如果两者之和为奇数,乙得1分,此游戏( )
A.是公平的 B.对乙有利 C.对甲有利 D.以上都不对
7.如图,是由半圆和长方形拼成一个转盘,其中点O是半圆的圆心,半圆的直径与长方形的宽相等,直径和过点O的长方形长边的平行线,把转盘分成4个部分若任意转动指针,指针停止的位置是等可能的,则指针指向阴影部分的概率是( )
A. B. C. D.因长方形的长没有告知,所以概率不确定
8.如图,正方形 中,点 是以 为直径的半圆与对角线 的交点.现随机向正方形 内投掷一枚小针,则针尖落在阴影区域的概率为( )
A. B. C. D.
9.学生甲手中有4,6,8三张扑克牌,学生乙手中有3,5,10三张扑克牌,现每人从各自手中随机取出一张牌进行比较,数字大者胜,在该游戏中( )
A.甲获胜的概率大 B.乙获胜的概率大
C.两人获胜概率一样大 D.不能确定
10.下列游戏对双方公平的是( )
A.随意转动被等分成3个扇形,且分别均匀涂有红、黄、绿三种颜色的转盘,若指针指向绿色区域,则小明胜,否则小亮胜
B.从一个装有3个红球,2个黄球和2个黑球(这些球除颜色外完全相同)的袋中任意摸出一个球,若是红球,则小明胜,否则小亮胜
C.投掷一枚均匀的正方体形状的骰子,若偶数点朝上,则小明胜,若是奇数点朝上,则小亮胜
D.从分别标有数1,2,3,4,5的五张纸条中,任意抽取一张,若抽到的纸条所标的数字为偶数,则小明胜,若抽到的纸条所标的数字为奇数,则小亮胜
11.如图,正六边形中,点A在一边上运动,AO交六边形的另一边于B,过O作AB的垂线交六边形于C,D,形成如图所示的阴影部分.小姜设计了两个方案:①把如图所示的飞镖盘纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是.②以O为旋转中心,把六边形做成转盘,则指针落在阴影部分的概率是.那么以上两种方案正确的是( )
A.①② B.① C.② D.①②都错误
12.22届年级组董老师为学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小赵同学同时转动A盘和B盘,她赢得游戏的概率是( )
A. B. C. D.
二、填空题
13.袋中装有一个红球和二个黄球,它们除了颜色外都相同,随机从中摸出一球,记录下颜色后放回袋中,充分摇匀后,再随机摸出一球,两次都摸到红球的概率是 。
14.李老师在墙上挂了一幅如图所示的图案,假设可以在图中随意钉钉子,那么这个钉子钉在阴影部分(边界忽略不计)的概率是 .
15.在四个完全相同的球上分别标上数字1、2、3、4,从这四个球 中随机取出一个球记所标数字为,放回后再随机取出一个球记所标数字为,则的概率为 .
16.已知A,B两组卡片共5张,A中三张分别写有数字2,4,6,B中两张分别写有3,5,它们除数字外没有任何区别.现制定这样一个游戏规则:随机地分别从A,B中各抽取一张,若所选出的两数之积为3的倍数,则甲获胜;否则乙获胜.这样的游戏规则对 有利.
三、解答题
17.在5张相同的小纸条上,分别写有:①;②;③1;④乘法;⑤加法.将这5张小纸条做成5支签,①、②、③放在不透明的盒子A中搅匀,④、⑤放在不透明的盒子B中搅匀.
(1)从盒子中任意抽出支签,抽到无理数的概率是 ;
(2)先从盒子中任意抽出支签,再从盒子中任意抽出支签,求抽到的个实数进行相应的运算后结果是无理数的概率.
18.如图,从一个大正方形中截去面积为3cm 和12cm 的两个小正方形,若随机向大正方形内投一粒米,求米粒落在图中阴影部分的概率.
19.一个不透明的布袋里装有20个除颜色外均相同的小球,其中白球有x个,红球有个,其他均为黄球.现从布袋中随机摸出一个球,若是红球则甲同学获胜,若为黄球,则乙同学获胜.
(1)当时,谁获胜的可能性大?
(2)要使游戏对甲乙双方是公平的,x应取何值?
20.暑假将至,某商场为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被均匀地分为20份),并规定:顾客每 200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.若某顾客购物300元.
(1)求他此时获得购物券的概率是多少?
(2)他获得哪种购物券的概率最大?请说明理由.
答案解析部分
1.【答案】B
【解析】解:由于显示屏每间隔4分钟显示一次火车班次的信息,显示时间持续1分钟,
所以显示屏上每隔5分钟就有一分钟的显示时间,
某人到达该车站时正好显示火车班次信息的概率是 .
故答案为:B.
2.【答案】D
【解析】解:A、让转盘自由转动一次,停止后指针落在阴影区域内的概率为;
B、让转盘自由转动一次,停止后指针落在阴影区域内的概率为;
C、让转盘自由转动一次,停止后指针落在阴影区域内的概率为;
D、让转盘自由转动一次,停止后指针落在阴影区域内的概率为;
∵,
∴让转盘自由转动一次,停止后指针落在阴影区域内的概率最大的转盘是选项D的转盘.
故答案为:D.
3.【答案】B
【解析】解:可能的结果有4种:2,3,4;2,3,5;2,4,5;3,4,5.其中,可以构成钝角三角形的有2种情形:2,3,4;2,4,5.∴能组成三角形的概率为= .故答案为:B.
4.【答案】B
【解析】画树状图得:
共有12种等可能性,其中符合条件的有2种,所以P= .
故答案为: B.
5.【答案】A
【解析】解:第一个转盘转出红色的概率为,转出蓝色的概率为,第二个转盘转出红色的概率为,转出蓝色的概率为,然后根据红色与蓝色可配成紫色可得:配成紫色的概率为×+×=.
故答案为:A.
6.【答案】C
【解析】解:甲、乙两人各自掷一个普通的正方体骰子,共有36种结果,其中两者之积为偶数有27种,两者之积为奇数有9种,两者之积为偶数的概率为 ,则两者之积为奇数的概率为 , ,
故答案为:C.
7.【答案】A
【解析】解:转动转盘指针转过的角度为360° ,指针在阴影部分转过的角度为90° ,
转盘停止转动时指针指向阴影部分的概率是: .
故答案为:A.
8.【答案】B
【解析】解:连接BE,如图,
∵AB为直径,
∴∠AEB=90°,
而AC为正方形的对角线,
∴AE=BE=CE,
∴弓形AE的面积=弓形BE的面积,
∴阴影部分的面积=△BCE的面积,
∴镖落在阴影部分的概率= .
故答案为:B.
9.【答案】A
【解析】解:由题意知,甲取出4时,乙有3,5,10共三种可能,其中甲获胜有1种可能;
甲取出6时,乙有3,5,10共三种可能,其中甲获胜有2种可能;
甲取出8时,乙有3,5,10共三种可能,其中甲获胜有2种可能;
∴甲获胜的概率为 ,则乙获胜的概率为
∵
∴甲获胜的概率大
故答案为:A.
10.【答案】C
【解析】解:A中:P(小明胜)=P(小亮胜)=,P(小明胜)<P(小亮胜);不公平
B中:P(小明胜)=P(小亮胜)=,P(小明胜)>P(小亮胜);不公平
C中:P(小明胜)= P(小亮胜)=,P(小明胜)=P(小亮胜);公平
D中:P(小明胜)=P(小亮胜)=,P(小明胜)>P(小亮胜);不公平
故选C.
11.【答案】C
【解析】解:∵共正六边形的中心的直线能将正六边形平分,
∴当AB⊥CD时,两条直线能将正六边形平均分成四份,
∴阴影部分的面积是整个正六边形的面积的,
∴飞镖落在阴影部分和指针指向阴影部分的概率均为,
∴②均正确.
故选C.
12.【答案】C
【解析】解:∵B盘中蓝色扇形区域所占的圆心角为120°,
∴B盘红色扇形区域所占的圆心角为240°,
∴B盘中:S红色扇形=2S蓝色扇形,
画树状图如下:
∴一共有9种等可能的结果,其中一个转盘转出了红色、另一个转盘转出了蓝色的有3种情况,
∴小赵同学同时转动A盘和B盘,她赢得游戏的概率是=.
故答案为:C.
13.【答案】
【解析】解:
红 黄1 黄2
红 红红 黄1红 黄2红
黄1 红黄1 黄1黄1 黄2黄1
黄2 红黄2 黄1黄2 黄2黄2
由表可知两次摸球共有9种等可能结果,其中两次都是红球的只有1种,
∴P(红红)=。
故答案为:
14.【答案】
【解析】解:设阴影部分的面积为 ,则整个图形的面积为 ,
则:P(钉子钉在阴影部分)= .
故答案为:
15.【答案】
【解析】解:a有4种可能,b也有4种可能,
∴共44=16种可能
其中, 的可能有6种情况:
∴其概率为
故答案为:
16.【答案】甲
【解析】画树状图如下:
共有6种等可能的结果,甲获胜的情况有4种,故P(甲获胜) ,
∴这样的游戏规则对甲有利.
17.【答案】(1)
(2)解:树状图画出所有情况为:
即抽签的组合有12种,分别为:
组合情况 运算结果 运算结果是否是无理数
第一种组合 ,,乘法 否
第二种组合 ,,加法 是
第三种组合 ,,乘法 是
第四种组合 ,,加法 是
第五种组合 ,,乘法 否
第六种组合 ,,加法 是
第七种组合 ,,乘法 是
第八种组合 ,,加法 是
第九种组合 ,,乘法 是
第十种组合 ,,加法 是
第十一种组合 ,,乘法; 是
第十二种组合 ,,加法 是
对应的组合运算结果共12个,其中运算结果为无理数的有10个,
故抽到的2个实数进行相应的运算后结果是无理数的概率为.
【解析】解:(1)∵,
∴三个数中,无理数有与两个,
∴ 从盒子A中任意抽出1支签,抽到无理数的概率是;
故答案为:;
18.【答案】解:∵两个空白正方形的面积分别为12 cm 和3 cm ,
∴边长分别为cm和cm,
∴大正方形的边长为cm,
∴大正方形的面积为cm ,
∴阴影部分的面积为27-12-3=12 cm ,
∴米粒落在图中阴影部分的概率.
19.【答案】(1)解:当时,则红球有10个,黄球有5个,
红球的个数多于黄球的个数,
摸到红球的可能性更大,
当时,甲同学获胜可能性大;
(2)解:要使游戏对甲乙双方公平,必须有:
解得;
当时,游戏对甲乙双方是公平的.
20.【答案】(1)解:∵转盘被均匀地分为20份,他此时获得购物券的有10份,
∴他此时获得购物券的概率是:=
(2)解:∵P(获得200元购物券)=,P(获得100元购物券)=,P(获得50元购物券)==,
∴他获得50元购物券的概率最大.
【解析】【分析】(1)根据 转盘被均匀地分为20份,他此时获得购物券的有10份, 求概率即可;
(2)先求出 P(获得200元购物券)=,P(获得100元购物券)=,P(获得50元购物券)==, 再求解即可。
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
