第14章 勾股定理测试卷(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
2024华东师大版八年级数学上学期单元测试卷
第14章 勾股定理
时间:60分钟 满分:100分
一、选择题(每小题3分,共30分)
1.直角三角形中∠A,∠B,∠C所对的边分别为a,b,c,且∠C=90°.若a2=9,b2=16,则c2等于 ( )
A.5 B.7 C.25 D.49
2.下列各组数中,以它们为边不能构成直角三角形的是 ( )
A.3,4,5 B.6,8,10 C.9,12,15 D.5,6,7
3.如图,长方形ABCD中,AB=3,AD=1,点A,B在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于点M,则点M表示的数为 ( )
A.-1 B. C.-1 D.
4.如图,点E在正方形ABCD的内部,且∠AEB=90°,AE=6,BE=8,则阴影部分的面积是 ( )
A.80 B.76 C.60 D.48
5.一架长10 m的梯子,斜靠在一面竖直的墙上,这时梯足距离墙角6 m,若梯子的顶端下滑2 m,则梯足将滑动 ( )
A.0 m B.2 m C.1 m D.3 m
6.如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=10,如果△DAB的面积为40,那么DC的长为 ( )
A.6 B.7 C.8 D.9
7.如图,网格中的小正方形的边长为1,且点A,B,P都在小正方形的格点上,则∠PAB+∠PBA= ( )
A.30° B.60° C.45° D.75°
8.如图,有一个由传感器控制的灯A,装在门上方离地4.5 m的墙上,任何物体只要移至该灯周围5 m及5 m以内,灯就会自动发光.一个身高1.5 m的学生要走到离门多远的地方,灯刚好发光 ( )
A.5 m B.7 m C.4 m D.3 m
9.在我国古代数学著作《九章算术》的第九章《勾股》中记载了这样一个问题:
“今有开门去阃一尺,不合二寸.问门广几何 ”其大意是:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB是(1尺=10寸) ( )
A.101寸 B.100寸 C.52寸 D.96寸
10.如图,圆柱形容器的高为0.9 m,底面周长为1.2 m,在容器内壁离容器底部0.3 m的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器顶部0.2 m,且与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 ( )
A.1.3 m B.1.2 m C.1.1 m D.1 m
二、填空题(每小题3分,共18分)
11.木工师傅要做一扇长方形纱窗,做好后量得长为6分米,宽为4分米,对角线为7分米,则这扇纱窗 (填“合格”或“不合格”).
12.已知a,b,c是△ABC的三边长,且满足关系+|a-b|=0,则△ABC的形状为 .
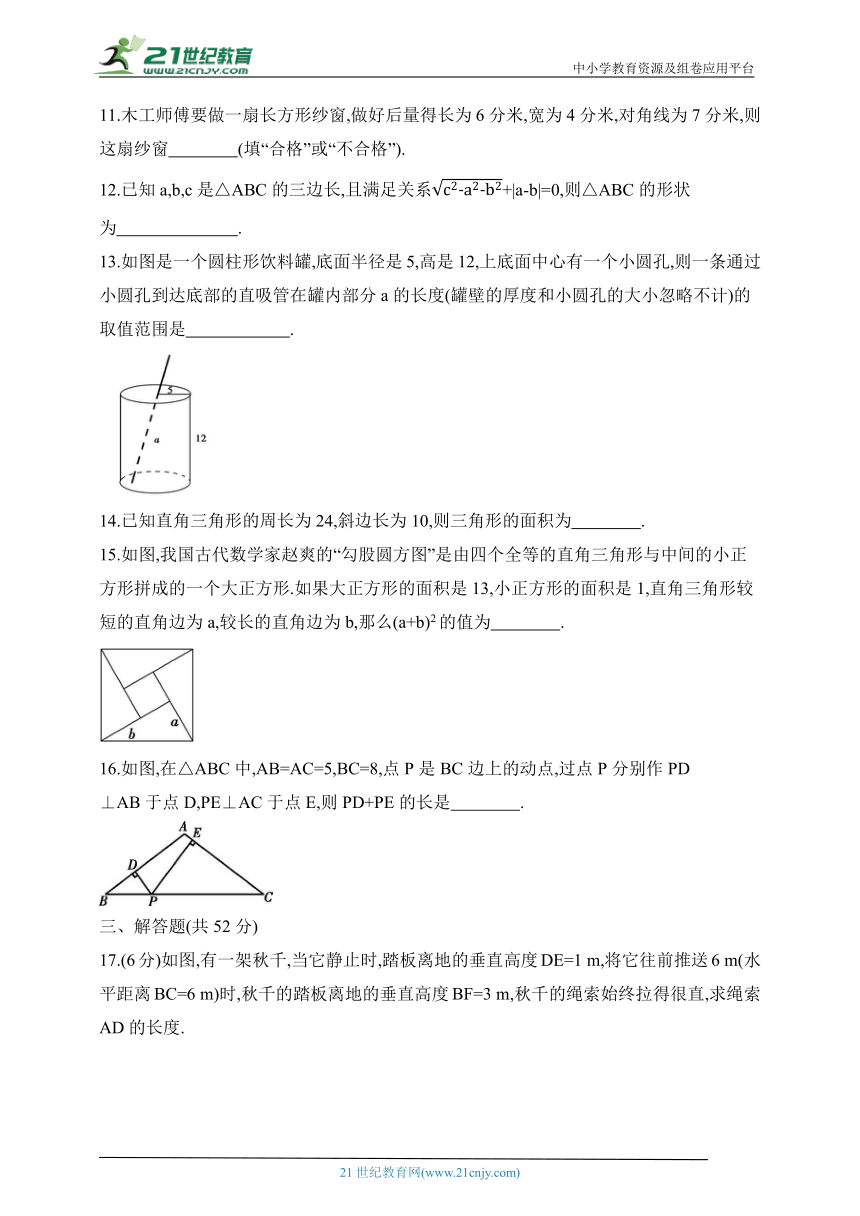
13.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条通过小圆孔到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是 .
14.已知直角三角形的周长为24,斜边长为10,则三角形的面积为 .
15.如图,我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,那么(a+b)2的值为 .
16.如图,在△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P分别作PD
⊥AB于点D,PE⊥AC于点E,则PD+PE的长是 .
三、解答题(共52分)
17.(6分)如图,有一架秋千,当它静止时,踏板离地的垂直高度DE=1 m,将它往前推送6 m(水平距离BC=6 m)时,秋千的踏板离地的垂直高度BF=3 m,秋千的绳索始终拉得很直,求绳索AD的长度.
18.(7分)古埃及人曾用下面的方法得到直角.如图1,他们用13个等距的结把一根绳子分成等长的12段(以结为端点),一个人站在A处同时握住绳子的第1个结和第13个结,另外两个人分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.
(1)你能说说其中的原理吗
(2)请你仿照上面的方法,用绳子在图2中设计一种不同于图1的直角三角形.(只需画出示意图)
图1 图2
19.(8分)如图,在△ABC中,D是BC边上的中点,DE⊥BC于点D,交AB边于点E,且BE2-EA2=AC2.
(1)判断△ABC的形状并说明理由;
(2)若DE=3,BD=4,求AE的长.
20.(9分)如图,两个村子A,B在河的同侧,A,B两村到河边CD的距离分别为AC=1千米,BD=3千米,已知CD=3千米.现要在河边CD上建造一水厂,向A,B两村送自来水.铺设水管的费用为每千米 20 000 元.
(1)请你在CD上确定水厂位置O,使铺设水管的费用最省;
(2)求出(1)中铺设水管的总费用W.
21.(10分)勾股定理神秘而美妙,它的证法多样,其巧妙之处也各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:如图1,连接DB,CD,过点D作BC边上的高DF,则DF=EC=b-a.∵S四边形ADCB
=S△ACD+S△ABC=b2+ab,S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),∴b2+ab=c2+a(b-a),
∴a2+b2=c2.
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
图1 图2
22.(12分)如图,在△ABC中,AB=5 cm,BC=3 cm.若点P从点A出发,以每秒2 cm的速度沿折线A—C—B—A运动,设运动时间为t s(t>0).
(1)当点P在AC上,且满足PA=PB时,求t的值;
(2)若点P恰好在∠BAC的平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形(PC≠BC).
参考答案与解析
1.C
2.D
3.A AC===,则AM=.∵点A表示的数为-1,∴点M表示的数为-1.
4.B 根据勾股定理得,AB2=AE2+BE2=62+82=100,故S正方形ABCD=100.又S△ABE=×
6×8=24,所以S阴影部分=S正方形ABCD-S△ABE=76.
5.B 如图,OB=6 m,AB=CD=10 m,∴在Rt△AOB中,OA==8 m.∵AC
=2 m,∴OC=OA-AC=6 m.在Rt△COD中,OD==8 m,∴BD=OD-OB=8-
6=2(m).
6.A ∵∠C=90°,∴△DAB的面积=×DA×BC,∴×10×BC=40,解得BC=8.由勾股定理得,CD===6,故选A.
7.C 如图,延长AP交格点于点D,连接BD,∵PD2=BD2=12+22=5,PB2=12+32=10,∴
PD2+DB2=PB2,∴∠PDB=90°.又PD=BD,∴△PDB是等腰直角三角形,∴∠PAB+
∠PBA=∠DPB=45°.
8.C 如图,设CD表示该学生的身高,点C到点A的距离为5 m,则CD=1.5 m,AC
=5 m.过点C作CE⊥AB于点E.由题意可知,BE=CD=1.5 m,所以AE=AB-BE=4.5
-1.5=3(m).在Rt△ACE中,由勾股定理得CE==4(m),所以BD=CE=4 m,故一个身高1.5 m的学生要走到离门4 m远的地方,灯刚好发光.
9.A 如图,过点D作DE⊥AB于点E,则DE=10寸.设单门的宽度AO=x寸,则AE=(x-1)寸.根据勾股定理,得AD2=DE2+AE2,即x2=102+(x-1)2,解得x=50.5,所以AB=101寸.
10.D 如图,由题意得A'D=0.6 m,BD=0.8 m,∴A'B==
=1(m).
11.不合格 ∵42+62=52≠72=49,∴这扇纱窗不是长方形,故不合格.
12.等腰直角三角形 由+|a-b|=0,得c2-a2-b2=0,且a-b=0,即a2+b2= c2,a=b,
∴△ABC是等腰直角三角形.
13.12≤a≤13 如图,设点O是下底面的中心,点A是下底面的边缘上的一点,点B是上底面的中心,当吸管底部在O点时,吸管在罐内部分a的长度最短,此时a的长等于饮料罐的高,即a=12.当吸管底部在A点时,吸管在罐内部分a的长度最长,此时a的长等于线段AB的长.在Rt△ABO中,AB2=AO2+BO2=52+122=132,所以AB
=13,此时a=13.综上,a的长度的取值范围是12≤a≤13.
14.24 设该直角三角形两直角边长为a,b,∵该直角三角形的周长为24,其斜边长为10,∴a+b=14,由勾股定理得,a2+b2=102=100.∵(a+b)2=142,∴a2+b2+2ab=196,即ab
=48,∴直角三角形的面积=ab=24.
15.25 由题图可知4×ab=2ab=13-1=12,a2+b2=13,所以(a+b)2=a2+b2+2ab=13+12=
25.
16.4.8 如图,过点A作AF⊥BC于点F,连接AP.在△ABC中,∵AB=AC=5,BC=
8,∴BF=4.在Rt△ABF中,由勾股定理,得AF==3.∵S△ABC=S△ABP+S△APC,
∴×8×3=×5PD+×5PE,即12=×5(PD+PE),则PD+PE=4.8.
17.解:设秋千的绳索长为x m,则AB=x m,AC=(x-2)m.(2分)
在Rt△ABC中,根据勾股定理可得x2=62+(x-2)2,解得x=10. (5分)
答:绳索AD的长度是10 m. (6分)
18.解:(1)设相邻两结点之间的距离为a,则此三角形三边的长分别为3a,4a,5a.
∵(3a)2+(4a)2=(5a)2,∴以3a,4a,5a为边长的三角形是直角三角形,且长为5a的边所对的角为直角. (5分)
(2)如图所示.(答案不唯一,符合题意即可)
(7分)
19.解:(1)△ABC是直角三角形. (1分)
理由:连接CE,如图.
∵D是BC边上的中点,DE⊥BC,∴CE=BE.
∵BE2-EA2=AC2,∴CE2-EA2=AC2,即EA2+AC2=CE2,
∴△ACE是直角三角形,且∠A=90°,∴△ABC是直角三角形. (4分)
(2)∵DE⊥BC,DE=3,BD=4,
∴BE==5=CE,∴AC2=EC2-AE2=25-AE2.
∵D是BC边上的中点,BD=4,∴BC=2BD=8.
在Rt△BAC中,BC2-BA2=64-(5+AE)2=AC2,
∴64-(5+AE)2=25-AE2,解得AE=.(8分)
20.解:(1)如图,延长AC到点M,使CM=AC,连接BM交CD于点O,点O就是所选择的位置. (4分)
(2)如图,连接OA,过点M作MN⊥BD,交BD的延长线于点N. (5分)
在Rt△BMN中,BN=BD+DN=4千米,MN=CD=3千米,
∴MB===5(千米), (7分)
∴最短路线AO+BO=MB=5千米,∴铺设水管的总费用W=5×20 000=100 000(元).
答:最省的铺设水管的总费用是100 000元. (9分)
“将军饮马”问题的解题通法
“将军饮马”问题是中考的热点问题之一,解决这类问题的关键在于找出两定点中任一点关于动点所在直线的对称点,再将另一点与对称点相连,连线与直线的交点即为所求的点.几何问题中求线段和的最小值时,通常有两种模型,即“将军饮马”和“两点之间线段最短”,当两点在直线同侧时,运用前者;当两点在直线异侧时,运用后者.通常情况下,求三角形或四边形的周长的最小值时,往往也是运用上述两种模型进行解题.
21.解:证明:连接BD,过点B作DE边上的高BF,则BF=b-a. (2分)
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab, (5分)
S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b-a), (8分)
∴ab+b2+ab=ab+c2+a(b-a),∴a2+b2=c2. (10分)
22.解:(1)∵AB=5 cm,BC=3 cm,∠C=90°,∴AC==4(cm).
由PA=PB,PA=2t cm,可得PB=2t cm,PC=(4-2t)cm.
在Rt△PCB中,PC2+CB2=PB2,即(4-2t)2+32=(2t)2,解得t=,
∴当t=时,PA=PB. (4分)
(2)当点P在∠BAC的平分线上时,如图1,过点P作PE⊥AB于点E,
此时BP=(7-2t)cm,PE=PC=(2t-4)cm,BE=5-4=1(cm).
在Rt△BEP中,PE2+BE2=BP2,即(2t-4)2+12=(7-2t)2,解得t=,
∴当t=时,点P在∠BAC的平分线上. (8分)
(3)t=或5时,△BCP为等腰三角形,且PC≠BC. (12分)
当点P在AC上时,∵△BCP为等腰三角形,∠ACB=90°,且PC≠BC,
∴不存在符合题意的点P.
当点P在AB上时,△BCP为等腰三角形,分为以下两种情况:
①当CP=PB时,如图2,过点P作PF⊥BC于点F,∴BF=BC= cm,
易得PB=AB,即2t-3-4=,解得t=.
②当PB=BC时,2t-3-4=3,解得t=5.
图1 图2
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版八年级数学上学期单元测试卷
第14章 勾股定理
时间:60分钟 满分:100分
一、选择题(每小题3分,共30分)
1.直角三角形中∠A,∠B,∠C所对的边分别为a,b,c,且∠C=90°.若a2=9,b2=16,则c2等于 ( )
A.5 B.7 C.25 D.49
2.下列各组数中,以它们为边不能构成直角三角形的是 ( )
A.3,4,5 B.6,8,10 C.9,12,15 D.5,6,7
3.如图,长方形ABCD中,AB=3,AD=1,点A,B在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于点M,则点M表示的数为 ( )
A.-1 B. C.-1 D.
4.如图,点E在正方形ABCD的内部,且∠AEB=90°,AE=6,BE=8,则阴影部分的面积是 ( )
A.80 B.76 C.60 D.48
5.一架长10 m的梯子,斜靠在一面竖直的墙上,这时梯足距离墙角6 m,若梯子的顶端下滑2 m,则梯足将滑动 ( )
A.0 m B.2 m C.1 m D.3 m
6.如图,在Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=10,如果△DAB的面积为40,那么DC的长为 ( )
A.6 B.7 C.8 D.9
7.如图,网格中的小正方形的边长为1,且点A,B,P都在小正方形的格点上,则∠PAB+∠PBA= ( )
A.30° B.60° C.45° D.75°
8.如图,有一个由传感器控制的灯A,装在门上方离地4.5 m的墙上,任何物体只要移至该灯周围5 m及5 m以内,灯就会自动发光.一个身高1.5 m的学生要走到离门多远的地方,灯刚好发光 ( )
A.5 m B.7 m C.4 m D.3 m
9.在我国古代数学著作《九章算术》的第九章《勾股》中记载了这样一个问题:
“今有开门去阃一尺,不合二寸.问门广几何 ”其大意是:如图,推开两扇门(AD和BC),门边缘D,C两点到门槛AB的距离是1尺,两扇门的间隙CD为2寸,则门宽AB是(1尺=10寸) ( )
A.101寸 B.100寸 C.52寸 D.96寸
10.如图,圆柱形容器的高为0.9 m,底面周长为1.2 m,在容器内壁离容器底部0.3 m的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器顶部0.2 m,且与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 ( )
A.1.3 m B.1.2 m C.1.1 m D.1 m
二、填空题(每小题3分,共18分)
11.木工师傅要做一扇长方形纱窗,做好后量得长为6分米,宽为4分米,对角线为7分米,则这扇纱窗 (填“合格”或“不合格”).
12.已知a,b,c是△ABC的三边长,且满足关系+|a-b|=0,则△ABC的形状为 .
13.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条通过小圆孔到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是 .
14.已知直角三角形的周长为24,斜边长为10,则三角形的面积为 .
15.如图,我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,那么(a+b)2的值为 .
16.如图,在△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P分别作PD
⊥AB于点D,PE⊥AC于点E,则PD+PE的长是 .
三、解答题(共52分)
17.(6分)如图,有一架秋千,当它静止时,踏板离地的垂直高度DE=1 m,将它往前推送6 m(水平距离BC=6 m)时,秋千的踏板离地的垂直高度BF=3 m,秋千的绳索始终拉得很直,求绳索AD的长度.
18.(7分)古埃及人曾用下面的方法得到直角.如图1,他们用13个等距的结把一根绳子分成等长的12段(以结为端点),一个人站在A处同时握住绳子的第1个结和第13个结,另外两个人分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.
(1)你能说说其中的原理吗
(2)请你仿照上面的方法,用绳子在图2中设计一种不同于图1的直角三角形.(只需画出示意图)
图1 图2
19.(8分)如图,在△ABC中,D是BC边上的中点,DE⊥BC于点D,交AB边于点E,且BE2-EA2=AC2.
(1)判断△ABC的形状并说明理由;
(2)若DE=3,BD=4,求AE的长.
20.(9分)如图,两个村子A,B在河的同侧,A,B两村到河边CD的距离分别为AC=1千米,BD=3千米,已知CD=3千米.现要在河边CD上建造一水厂,向A,B两村送自来水.铺设水管的费用为每千米 20 000 元.
(1)请你在CD上确定水厂位置O,使铺设水管的费用最省;
(2)求出(1)中铺设水管的总费用W.
21.(10分)勾股定理神秘而美妙,它的证法多样,其巧妙之处也各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:如图1,连接DB,CD,过点D作BC边上的高DF,则DF=EC=b-a.∵S四边形ADCB
=S△ACD+S△ABC=b2+ab,S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),∴b2+ab=c2+a(b-a),
∴a2+b2=c2.
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
图1 图2
22.(12分)如图,在△ABC中,AB=5 cm,BC=3 cm.若点P从点A出发,以每秒2 cm的速度沿折线A—C—B—A运动,设运动时间为t s(t>0).
(1)当点P在AC上,且满足PA=PB时,求t的值;
(2)若点P恰好在∠BAC的平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形(PC≠BC).
参考答案与解析
1.C
2.D
3.A AC===,则AM=.∵点A表示的数为-1,∴点M表示的数为-1.
4.B 根据勾股定理得,AB2=AE2+BE2=62+82=100,故S正方形ABCD=100.又S△ABE=×
6×8=24,所以S阴影部分=S正方形ABCD-S△ABE=76.
5.B 如图,OB=6 m,AB=CD=10 m,∴在Rt△AOB中,OA==8 m.∵AC
=2 m,∴OC=OA-AC=6 m.在Rt△COD中,OD==8 m,∴BD=OD-OB=8-
6=2(m).
6.A ∵∠C=90°,∴△DAB的面积=×DA×BC,∴×10×BC=40,解得BC=8.由勾股定理得,CD===6,故选A.
7.C 如图,延长AP交格点于点D,连接BD,∵PD2=BD2=12+22=5,PB2=12+32=10,∴
PD2+DB2=PB2,∴∠PDB=90°.又PD=BD,∴△PDB是等腰直角三角形,∴∠PAB+
∠PBA=∠DPB=45°.
8.C 如图,设CD表示该学生的身高,点C到点A的距离为5 m,则CD=1.5 m,AC
=5 m.过点C作CE⊥AB于点E.由题意可知,BE=CD=1.5 m,所以AE=AB-BE=4.5
-1.5=3(m).在Rt△ACE中,由勾股定理得CE==4(m),所以BD=CE=4 m,故一个身高1.5 m的学生要走到离门4 m远的地方,灯刚好发光.
9.A 如图,过点D作DE⊥AB于点E,则DE=10寸.设单门的宽度AO=x寸,则AE=(x-1)寸.根据勾股定理,得AD2=DE2+AE2,即x2=102+(x-1)2,解得x=50.5,所以AB=101寸.
10.D 如图,由题意得A'D=0.6 m,BD=0.8 m,∴A'B==
=1(m).
11.不合格 ∵42+62=52≠72=49,∴这扇纱窗不是长方形,故不合格.
12.等腰直角三角形 由+|a-b|=0,得c2-a2-b2=0,且a-b=0,即a2+b2= c2,a=b,
∴△ABC是等腰直角三角形.
13.12≤a≤13 如图,设点O是下底面的中心,点A是下底面的边缘上的一点,点B是上底面的中心,当吸管底部在O点时,吸管在罐内部分a的长度最短,此时a的长等于饮料罐的高,即a=12.当吸管底部在A点时,吸管在罐内部分a的长度最长,此时a的长等于线段AB的长.在Rt△ABO中,AB2=AO2+BO2=52+122=132,所以AB
=13,此时a=13.综上,a的长度的取值范围是12≤a≤13.
14.24 设该直角三角形两直角边长为a,b,∵该直角三角形的周长为24,其斜边长为10,∴a+b=14,由勾股定理得,a2+b2=102=100.∵(a+b)2=142,∴a2+b2+2ab=196,即ab
=48,∴直角三角形的面积=ab=24.
15.25 由题图可知4×ab=2ab=13-1=12,a2+b2=13,所以(a+b)2=a2+b2+2ab=13+12=
25.
16.4.8 如图,过点A作AF⊥BC于点F,连接AP.在△ABC中,∵AB=AC=5,BC=
8,∴BF=4.在Rt△ABF中,由勾股定理,得AF==3.∵S△ABC=S△ABP+S△APC,
∴×8×3=×5PD+×5PE,即12=×5(PD+PE),则PD+PE=4.8.
17.解:设秋千的绳索长为x m,则AB=x m,AC=(x-2)m.(2分)
在Rt△ABC中,根据勾股定理可得x2=62+(x-2)2,解得x=10. (5分)
答:绳索AD的长度是10 m. (6分)
18.解:(1)设相邻两结点之间的距离为a,则此三角形三边的长分别为3a,4a,5a.
∵(3a)2+(4a)2=(5a)2,∴以3a,4a,5a为边长的三角形是直角三角形,且长为5a的边所对的角为直角. (5分)
(2)如图所示.(答案不唯一,符合题意即可)
(7分)
19.解:(1)△ABC是直角三角形. (1分)
理由:连接CE,如图.
∵D是BC边上的中点,DE⊥BC,∴CE=BE.
∵BE2-EA2=AC2,∴CE2-EA2=AC2,即EA2+AC2=CE2,
∴△ACE是直角三角形,且∠A=90°,∴△ABC是直角三角形. (4分)
(2)∵DE⊥BC,DE=3,BD=4,
∴BE==5=CE,∴AC2=EC2-AE2=25-AE2.
∵D是BC边上的中点,BD=4,∴BC=2BD=8.
在Rt△BAC中,BC2-BA2=64-(5+AE)2=AC2,
∴64-(5+AE)2=25-AE2,解得AE=.(8分)
20.解:(1)如图,延长AC到点M,使CM=AC,连接BM交CD于点O,点O就是所选择的位置. (4分)
(2)如图,连接OA,过点M作MN⊥BD,交BD的延长线于点N. (5分)
在Rt△BMN中,BN=BD+DN=4千米,MN=CD=3千米,
∴MB===5(千米), (7分)
∴最短路线AO+BO=MB=5千米,∴铺设水管的总费用W=5×20 000=100 000(元).
答:最省的铺设水管的总费用是100 000元. (9分)
“将军饮马”问题的解题通法
“将军饮马”问题是中考的热点问题之一,解决这类问题的关键在于找出两定点中任一点关于动点所在直线的对称点,再将另一点与对称点相连,连线与直线的交点即为所求的点.几何问题中求线段和的最小值时,通常有两种模型,即“将军饮马”和“两点之间线段最短”,当两点在直线同侧时,运用前者;当两点在直线异侧时,运用后者.通常情况下,求三角形或四边形的周长的最小值时,往往也是运用上述两种模型进行解题.
21.解:证明:连接BD,过点B作DE边上的高BF,则BF=b-a. (2分)
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab, (5分)
S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b-a), (8分)
∴ab+b2+ab=ab+c2+a(b-a),∴a2+b2=c2. (10分)
22.解:(1)∵AB=5 cm,BC=3 cm,∠C=90°,∴AC==4(cm).
由PA=PB,PA=2t cm,可得PB=2t cm,PC=(4-2t)cm.
在Rt△PCB中,PC2+CB2=PB2,即(4-2t)2+32=(2t)2,解得t=,
∴当t=时,PA=PB. (4分)
(2)当点P在∠BAC的平分线上时,如图1,过点P作PE⊥AB于点E,
此时BP=(7-2t)cm,PE=PC=(2t-4)cm,BE=5-4=1(cm).
在Rt△BEP中,PE2+BE2=BP2,即(2t-4)2+12=(7-2t)2,解得t=,
∴当t=时,点P在∠BAC的平分线上. (8分)
(3)t=或5时,△BCP为等腰三角形,且PC≠BC. (12分)
当点P在AC上时,∵△BCP为等腰三角形,∠ACB=90°,且PC≠BC,
∴不存在符合题意的点P.
当点P在AB上时,△BCP为等腰三角形,分为以下两种情况:
①当CP=PB时,如图2,过点P作PF⊥BC于点F,∴BF=BC= cm,
易得PB=AB,即2t-3-4=,解得t=.
②当PB=BC时,2t-3-4=3,解得t=5.
图1 图2
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
