人教版六年级下册数学《平面图形的周长与面积》课件(共23张ppt)
文档属性
| 名称 | 人教版六年级下册数学《平面图形的周长与面积》课件(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-03 08:17:06 | ||
图片预览







文档简介
(共23张PPT)
平面图形的周长和面积
人教版六年级下册总复习图形与几何
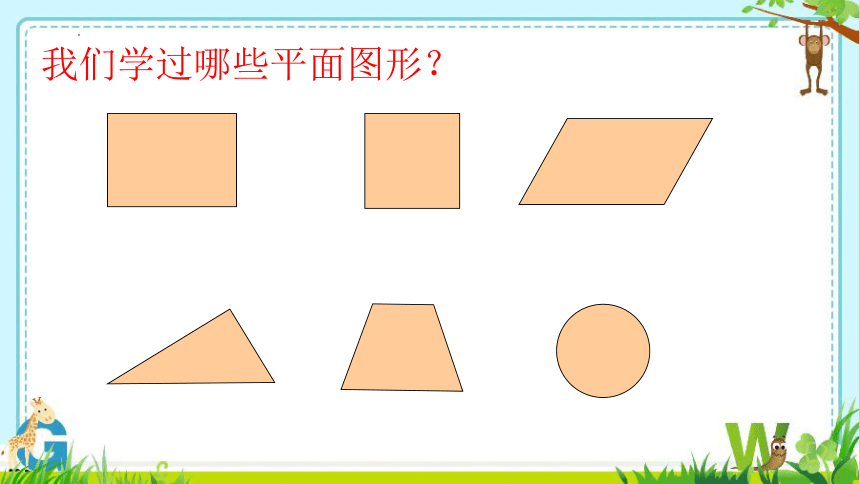
我们学过哪些平面图形?
1、平面图形的周长和面积的意义各是什么?
2、这些周长和面积公式各是怎样的?它们是怎样推导出来的?
复习提纲:
1、平面图形的周长和面积的意义各是什么?
2、这些周长和面积公式各是怎样的?它们是怎样推导出来的?
谁能说一说什么是平面图形的周长?
围成一个图形的所有边长的总和叫做这个图形的周长。
(周长采用长度单位,有:毫米、厘米、分米、米、千米等。)
那什么是平面图形的面积呢?
物体的表面或围成平面图形的大小叫做它们的面积。
(计量面积采用面积单位,有:平方厘米、平方分米、平方米、公顷、平方千米等。)
辨
一辩
一个边长是4厘米的正方形,它的周长和面积相等。你同意这个观点吗?说说你的理由。
周长和面积的意义不同,单位不同,不能比较大小。
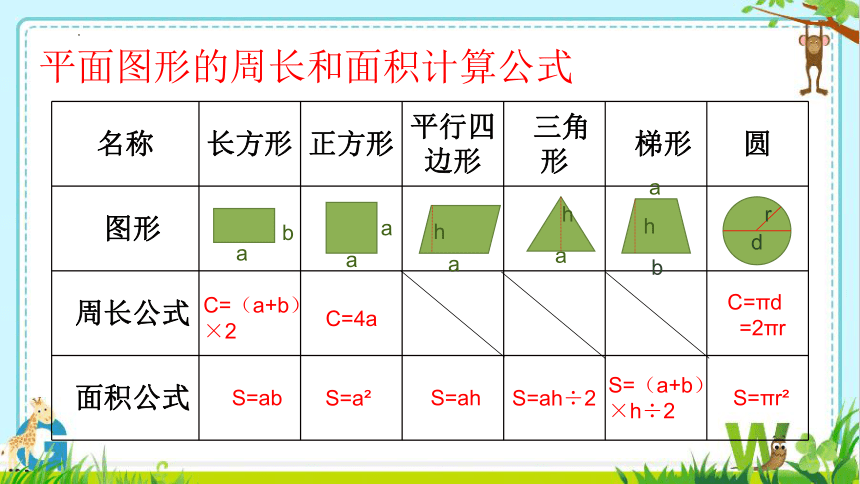
名称 长方形 正方形 平行四边形 三角形 梯形 圆
图形
周长公式
面积公式
a
b
a
a
h
a
a
h
a
h
b
d
r
C=(a+b)
×2
C=4a
C=πd
=2πr
S=ab
S=a
S=ah
S=(a+b)
×h÷2
S=πr
S=ah÷2
平面图形的周长和面积计算公式
三角形、平行四边形及梯形的周长应该怎样计算呢?
结合生活实际,求出各边的边长之和。
(1)小组交流整理平面图形的面积推导过程;
(2)小组选择一个你喜欢的图形说一说它的面积推导过程。
交流讨论
5 厘米
3 厘米
1平方厘米
=
×
小正方形的个数
长方形的面积
每排个数
长
排数
宽
=
×
1平方厘米
3厘米
3厘米
小正方形的个数
每排个数
排数
正方形面积
边长
边长
=
=
×
×
平行四边形的面积=底×高
三角形面积=底 ×高÷2
梯形面积=(上底+下底)×高÷2
圆的面积=πr
通过我们对面积推导过程的回顾,我们发现在推导过程中,它们还有内在的联系。你能不能通过摆图形的方法把它们的关系展示出来?
平面图形的周长和面积公式推导:
a
a
h
a
h
a
b
r
S =
S =
S =
S =
S =
S =
ab
ah
ah÷2
(a+b)h÷2
a
C =
C =
C =
(a+b)×2
4 a
2πr
πr2
a
h
b
一、计算下面各图形的周长和面积。(单位:米)
2
40
30
50
6
6
7.5
10.5
周长:30+40+50=120m
面积:30×40÷2=600m
周长:6+6+7.5+10.5=30m
面积:(6+10.5)×6÷2
=16.5×6÷2
=49.5m
2、求右面图形的面积。(单位:厘米)
8
15
10
25
9
15×8÷2 +(15+25)×10÷2 + 25×9
﹦60+200+225
﹦485(平方厘米)
S﹦ah÷2+ (a+b)h÷2 + ah
答:它的面积是485平方厘米。
1、面积相等的两个梯形一定可以拼成一个平行四边形。 ( )
2、面积相等的两个三角形形状也相同。( )
3、同底等高的两个三角形的面积一定相等。( )
4、周长相等的长方形和平行四边形,他们的面积一定相等。( )
5、底和高都是0.2厘米的三角形的面积是0.2平方厘米。( )
6、平行四边形的底越长,它的面积就越大。( )
7、三角形的面积是平行四边形面积的一半。( )
8、两个三角形的高相等,它们的面积就相等。( )
×
×
×
×
×
×
×
√
2.一片树林地的形状是梯形,它的上底是150米,下底是180米,高是60米,如果按每棵树占地10平方米计算,这片树林中约有多少棵树?
通过这节课的复习,
我们复习了什么?
你有哪些收获?
平面图形的周长和面积
人教版六年级下册总复习图形与几何
我们学过哪些平面图形?
1、平面图形的周长和面积的意义各是什么?
2、这些周长和面积公式各是怎样的?它们是怎样推导出来的?
复习提纲:
1、平面图形的周长和面积的意义各是什么?
2、这些周长和面积公式各是怎样的?它们是怎样推导出来的?
谁能说一说什么是平面图形的周长?
围成一个图形的所有边长的总和叫做这个图形的周长。
(周长采用长度单位,有:毫米、厘米、分米、米、千米等。)
那什么是平面图形的面积呢?
物体的表面或围成平面图形的大小叫做它们的面积。
(计量面积采用面积单位,有:平方厘米、平方分米、平方米、公顷、平方千米等。)
辨
一辩
一个边长是4厘米的正方形,它的周长和面积相等。你同意这个观点吗?说说你的理由。
周长和面积的意义不同,单位不同,不能比较大小。
名称 长方形 正方形 平行四边形 三角形 梯形 圆
图形
周长公式
面积公式
a
b
a
a
h
a
a
h
a
h
b
d
r
C=(a+b)
×2
C=4a
C=πd
=2πr
S=ab
S=a
S=ah
S=(a+b)
×h÷2
S=πr
S=ah÷2
平面图形的周长和面积计算公式
三角形、平行四边形及梯形的周长应该怎样计算呢?
结合生活实际,求出各边的边长之和。
(1)小组交流整理平面图形的面积推导过程;
(2)小组选择一个你喜欢的图形说一说它的面积推导过程。
交流讨论
5 厘米
3 厘米
1平方厘米
=
×
小正方形的个数
长方形的面积
每排个数
长
排数
宽
=
×
1平方厘米
3厘米
3厘米
小正方形的个数
每排个数
排数
正方形面积
边长
边长
=
=
×
×
平行四边形的面积=底×高
三角形面积=底 ×高÷2
梯形面积=(上底+下底)×高÷2
圆的面积=πr
通过我们对面积推导过程的回顾,我们发现在推导过程中,它们还有内在的联系。你能不能通过摆图形的方法把它们的关系展示出来?
平面图形的周长和面积公式推导:
a
a
h
a
h
a
b
r
S =
S =
S =
S =
S =
S =
ab
ah
ah÷2
(a+b)h÷2
a
C =
C =
C =
(a+b)×2
4 a
2πr
πr2
a
h
b
一、计算下面各图形的周长和面积。(单位:米)
2
40
30
50
6
6
7.5
10.5
周长:30+40+50=120m
面积:30×40÷2=600m
周长:6+6+7.5+10.5=30m
面积:(6+10.5)×6÷2
=16.5×6÷2
=49.5m
2、求右面图形的面积。(单位:厘米)
8
15
10
25
9
15×8÷2 +(15+25)×10÷2 + 25×9
﹦60+200+225
﹦485(平方厘米)
S﹦ah÷2+ (a+b)h÷2 + ah
答:它的面积是485平方厘米。
1、面积相等的两个梯形一定可以拼成一个平行四边形。 ( )
2、面积相等的两个三角形形状也相同。( )
3、同底等高的两个三角形的面积一定相等。( )
4、周长相等的长方形和平行四边形,他们的面积一定相等。( )
5、底和高都是0.2厘米的三角形的面积是0.2平方厘米。( )
6、平行四边形的底越长,它的面积就越大。( )
7、三角形的面积是平行四边形面积的一半。( )
8、两个三角形的高相等,它们的面积就相等。( )
×
×
×
×
×
×
×
√
2.一片树林地的形状是梯形,它的上底是150米,下底是180米,高是60米,如果按每棵树占地10平方米计算,这片树林中约有多少棵树?
通过这节课的复习,
我们复习了什么?
你有哪些收获?
