第23章图形的相似检测题(有答案)华师大版数学九年级上册
文档属性
| 名称 | 第23章图形的相似检测题(有答案)华师大版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 293.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-03 19:13:41 | ||
图片预览




文档简介
第23章检测题(后附答案)
(时间:100分钟 满分:120分)
一、精心选一选(每小题3分,共30分)
1.在平面直角坐标系中,将点A(-3,-2)向右平移5个单位长度得到点B,则点B关于y轴的对称点B′的坐标为( )
A.(2,2) B.(-2,2) C.(-2,-2) D.(2,-2)
2.已知△ABC与△A′B′C′是位似图形,相似比是1∶3,则△ABC与△A′B′C′的面积比是( )
A.1∶3 B.1∶6 C.1∶9 D.3∶1
3.已知x∶y=3∶2,则下列各式中不正确的是( )
A.= B.= C.= D.=
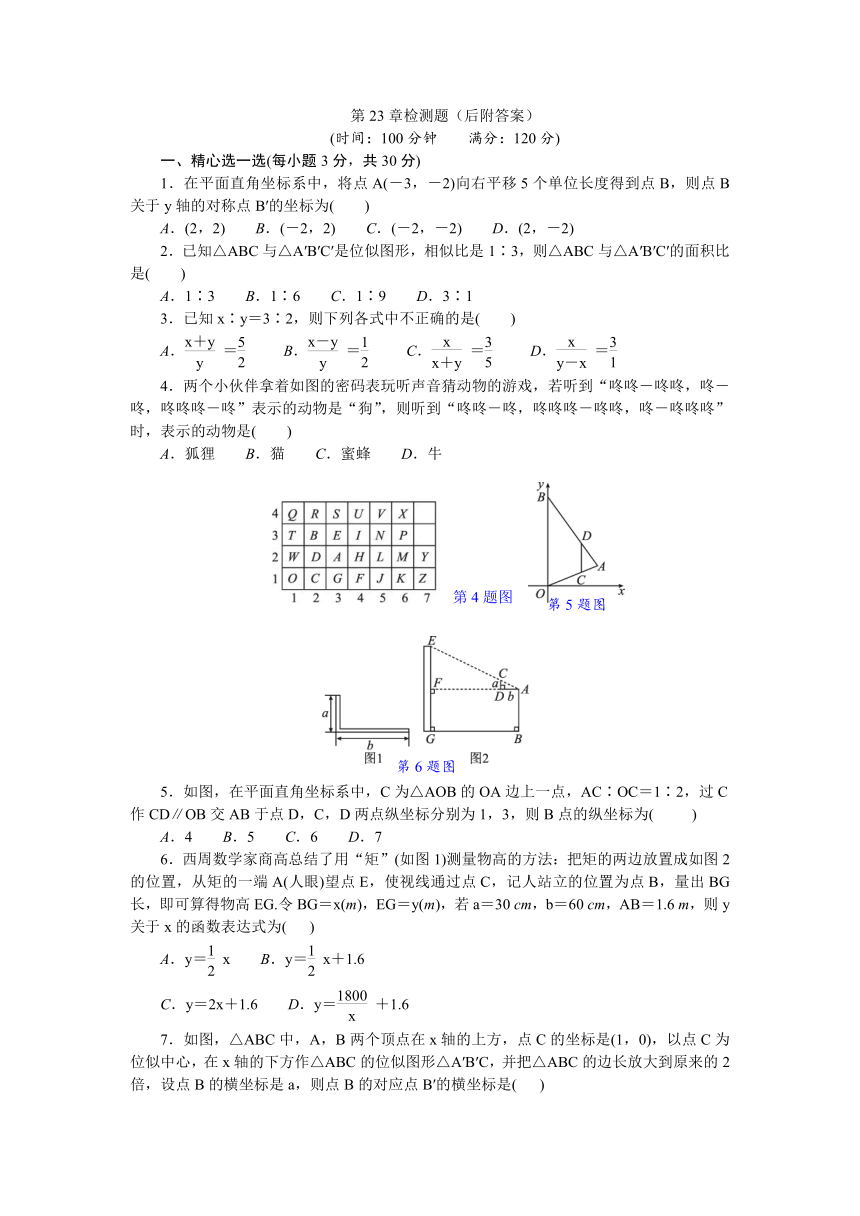
4.两个小伙伴拿着如图的密码表玩听声音猜动物的游戏,若听到“咚咚-咚咚,咚-咚,咚咚咚-咚”表示的动物是“狗”,则听到“咚咚-咚,咚咚咚-咚咚,咚-咚咚咚”时,表示的动物是( )
A.狐狸 B.猫 C.蜜蜂 D.牛
第4题图
5.如图,在平面直角坐标系中,C为△AOB的OA边上一点,AC∶OC=1∶2,过C作CD∥OB交AB于点D,C,D两点纵坐标分别为1,3,则B点的纵坐标为( )
A.4 B.5 C.6 D.7
6.西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m),EG=y(m),若a=30 cm,b=60 cm,AB=1.6 m,则y关于x的函数表达式为( )
A.y=x B.y=x+1.6
C.y=2x+1.6 D.y=+1.6
7.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
A.-2a+3 B.-2a+1 C.-2a+2 D.-2a-2
第9题图
8.如图,在矩形ABCD中,AB=6,BC=10,点E,F在AD边上,BF和CE交于点G,若EF=AD,则图中阴影部分的面积为( )
A.25 B.30 C.35 D.40
9.如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( )
A.15 B.20 C.25 D.30
10.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,点Q是线段AB上的动点,则PQ的最小值是( )
A. B. C. D.
二、细心填一填(每小题3分,共15分)
11.如图,在△ABC中,D,E分别是AB,AC的中点.若BC=12,则DE的长为__ __.
第11题图
12.如图,在△ABC中,点D在AB边上,点E在AC边上,请添加一个条
件__ _ _,使△ADE∽△ABC.
13.如图,AB∥CD∥EF.若=,BD=5,则DF=__ __.
14.如图,在平面直角坐标系中,△OAB与△OCD位似,位似中心是坐标原点O.若点A(4,0),点C(2,0),则△OAB与△OCD周长的比值是__ __.
第14题图 第15题图
15.如图,已知等腰△ABC的顶角∠BAC的大小为θ,点D为边BC上的动点(与B,C不重合),将AD绕点A沿顺时针方向旋转θ角度时点D落在D′处,连结BD′.给出下列结论:①△ACD≌△ABD′;②△ACB∽△ADD′;③当BD=CD时,△ADD′的面积取得最小值.其中正确的结论有__ _(填结论对应的序号).
三、用心做一做(共75分)
16.(8分)已知线段a,b,c满足==,且a+2b+c=26.
(1)判断a,2b,c,b2是否成比例;
(2)若实数x为a,b的比例中项,求x的值.
17.(9分)如图,在△ABC与△A′B′C′中,点D,D′分别在边BC,B′C′上,且△ACD∽△A′C′D′,若__ __,则△ABD∽△A′B′D′.
请从①=;②=;③∠BAD=∠B′A′D′这3个选项中选择一个作为条件(写序号),并加以证明.
18.(9分)在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(1,3),B(4,1),C(1,1).
(1)画出△ABC关于x轴成轴对称的△A1B1C1;
(2)在网格内以点O为位似中心,使△ABC与△A2B2C2的相似比为1∶2,请画出△A2B2C2.
19.(9分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C,A共线.已知:CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
20.(9分)如图,在△ABC中,D在AC上,DE∥BC,DF∥AB.
(1)求证:△DFC∽△AED;
(2)若CD=AC,求的值.
21.(10分)如图,在 ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由;
(2)连结AC,分别交BE,DF于点G,H,连结BD交AC于点O.若=,AE=4,求BC的长.
22.(10分)如图,矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O,BE与AC相交于点F.
(1)若BE平分∠CBD,求证:BF⊥AC;
(2)找出图中与△OBF相似的三角形,并说明理由;
(3)若OF=3,EF=2,求DE的长度.
23.(11分)(1)某学校“智慧方园”数学社团遇到这样一个题目:如图①,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=3,BO∶CO=1∶3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图②).
请回答:∠ADB=________,AB=________;
(2)请参考以上解决思路,解决问题:如图③,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=3,∠ABC=∠ACB=75°,BO∶OD=1∶3,求DC的长.
答案:
第23章检测题
(时间:100分钟 满分:120分)
1.( C )
2.( C )
3.( D )
4.( B )
5.( C )
6.( B )
7.( A )
8.( C )
9.( B )
10.( A )
11.__6__.
12.__∠ADE=∠B或∠AED=∠C或=(答案不唯一)__,使△ADE∽△ABC.
13.则DF=__10__.
14.__2__.
15.__①②③__(填结论对应的序号).
16.
解:(1)成比例 (2)x=±2
17.
解:③.理由如下:∵△ACD∽△A′C′D′,∴∠ADC=∠A′D′C′,∴∠ADB=∠A′D′B′,又∵∠BAD=∠B′A′D′,∴△ABD∽△A′B′D′.同理,选①也可以.故答案是:③(答案不唯一)
18
解:(1)∵△ABC的三个顶点的坐标分别是A(1,3),B(4,1),C(1,1),∴△ABC关于x轴成轴对称的△A1B1C1的坐标分别为A1(1,-3),B1(4,-1),C1(1,-1),连结A1C1,A1B1,B1C1得到△A1B1C1.如图所示,△A1B1C1即为所求
(2)由题意知:△A2B2C2在△ABC的对侧,则A2(-2,-6),B2(-8,-2),C2(-2,-2),顺次连结各点,得△A2B2C2.如图所示,△A2B2C2即为所求
19.
解:∵BC∥DE,∴△ABC∽△ADE,∴=,∴=,∴AB=17 m,答:河宽AB为17米
20.(9分
解:(1)∵DF∥AB,∴∠CDF=∠A,又∵DE∥BC,∴∠DCF=∠ADE,∴△DFC∽△AED (2)∵CD=AC,∴=,由(1)知△DFC和△AED的相似比为:=,故=()2=()2=
21.
解:(1)四边形BEDF为平行四边形,理由如下:∵四边形ABCD为平行四边形,∴∠ABC=∠ADC,∵∠ABE=∠CDF,∴∠EBF=∠EDF,∵四边形ABCD为平行四边形,∴AD∥BC,∴∠EDF=∠DFC=∠EBF,∴BE∥DF,∵AD∥BC,∴四边形BEDF为平行四边形 (2)设AG=2a,∵=,∴OG=3a,AO=5a,∵四边形ABCD为平行四边形,∴AO=CO=5a,CG=8a,∵AD∥BC,∴△AGE∽△CGB,∴==,∵AE=4,∴BC=16
22.
解:(1)如图,在矩形ABCD中,OD=OC,AB∥CD,∠BCD=90°,∴∠2=∠3=∠4,∠3+∠5=90°,∵DE=BE,∴∠1=∠2,又∵BE平分∠DBC,∴∠1=∠6,∴∠3=∠6,∴∠6+∠5=90°,∴BF⊥AC
(2)与△OBF相似的三角形有△ECF,△BAF.理由如下:∵DE=BE,∴∠1=∠2,又∵∠2=∠3.∴∠1=∠3,∵∠EFC=∠BFO,∴△ECF∽△OBF,∵DE=BE,∴∠1=∠2,又∵∠2=∠4,∴∠1=∠4,又∵∠BFA=∠OFB,∴△BAF∽△OBF
(3)由(2)知△OBF∽△ECF.∴=,∴=,即3CF=2BF,∵OA=OC,∴3OA=3CF+3OF,即3OA=2BF+9①,由(2)知△BAF∽△OBF,∴=,∴BF2=OF·AF,∴BF2=3(OA+3)②,联立①②,可得BF=1+或BF=1-(舍去),∴DE=BE=EF+BF=2+1+=3+
23.
解:(1)∵BD∥AC,∴∠ADB=∠OAC=75°.∵∠BOD=∠COA,∴△BOD∽△COA,∴==.又∵AO=3,∴OD=AO=,∴AD=AO+OD=4.∵∠BAD=30°,∠ADB=75°,∴∠ABD=180°-∠BAD-∠ADB=75°=∠ADB,∴AB=AD=4.故答案为:75°;4 (2)如图所示,过点B作BE∥AD交AC于点E,∵AC⊥AD,BE∥AD,∴∠DAC=∠BEA=90°.∵∠AOD=∠EOB,∴△AOD∽△EOB,∴==.∵BO∶OD=1∶3,∴==.∵AO=3,∴EO=,∴AE=4.∵∠ABC=∠ACB=75°,∴∠BAC=30°,AB=AC,∴AB=2BE.在Rt△AEB中,BE2+AE2=AB2,即(4)2+BE2=(2BE)2,解得BE=4,∴AB=AC=8,AD=12.在Rt△CAD中,AC2+AD2=CD2,即82+122=CD2,解得CD=4
(时间:100分钟 满分:120分)
一、精心选一选(每小题3分,共30分)
1.在平面直角坐标系中,将点A(-3,-2)向右平移5个单位长度得到点B,则点B关于y轴的对称点B′的坐标为( )
A.(2,2) B.(-2,2) C.(-2,-2) D.(2,-2)
2.已知△ABC与△A′B′C′是位似图形,相似比是1∶3,则△ABC与△A′B′C′的面积比是( )
A.1∶3 B.1∶6 C.1∶9 D.3∶1
3.已知x∶y=3∶2,则下列各式中不正确的是( )
A.= B.= C.= D.=
4.两个小伙伴拿着如图的密码表玩听声音猜动物的游戏,若听到“咚咚-咚咚,咚-咚,咚咚咚-咚”表示的动物是“狗”,则听到“咚咚-咚,咚咚咚-咚咚,咚-咚咚咚”时,表示的动物是( )
A.狐狸 B.猫 C.蜜蜂 D.牛
第4题图
5.如图,在平面直角坐标系中,C为△AOB的OA边上一点,AC∶OC=1∶2,过C作CD∥OB交AB于点D,C,D两点纵坐标分别为1,3,则B点的纵坐标为( )
A.4 B.5 C.6 D.7
6.西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m),EG=y(m),若a=30 cm,b=60 cm,AB=1.6 m,则y关于x的函数表达式为( )
A.y=x B.y=x+1.6
C.y=2x+1.6 D.y=+1.6
7.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
A.-2a+3 B.-2a+1 C.-2a+2 D.-2a-2
第9题图
8.如图,在矩形ABCD中,AB=6,BC=10,点E,F在AD边上,BF和CE交于点G,若EF=AD,则图中阴影部分的面积为( )
A.25 B.30 C.35 D.40
9.如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( )
A.15 B.20 C.25 D.30
10.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,点Q是线段AB上的动点,则PQ的最小值是( )
A. B. C. D.
二、细心填一填(每小题3分,共15分)
11.如图,在△ABC中,D,E分别是AB,AC的中点.若BC=12,则DE的长为__ __.
第11题图
12.如图,在△ABC中,点D在AB边上,点E在AC边上,请添加一个条
件__ _ _,使△ADE∽△ABC.
13.如图,AB∥CD∥EF.若=,BD=5,则DF=__ __.
14.如图,在平面直角坐标系中,△OAB与△OCD位似,位似中心是坐标原点O.若点A(4,0),点C(2,0),则△OAB与△OCD周长的比值是__ __.
第14题图 第15题图
15.如图,已知等腰△ABC的顶角∠BAC的大小为θ,点D为边BC上的动点(与B,C不重合),将AD绕点A沿顺时针方向旋转θ角度时点D落在D′处,连结BD′.给出下列结论:①△ACD≌△ABD′;②△ACB∽△ADD′;③当BD=CD时,△ADD′的面积取得最小值.其中正确的结论有__ _(填结论对应的序号).
三、用心做一做(共75分)
16.(8分)已知线段a,b,c满足==,且a+2b+c=26.
(1)判断a,2b,c,b2是否成比例;
(2)若实数x为a,b的比例中项,求x的值.
17.(9分)如图,在△ABC与△A′B′C′中,点D,D′分别在边BC,B′C′上,且△ACD∽△A′C′D′,若__ __,则△ABD∽△A′B′D′.
请从①=;②=;③∠BAD=∠B′A′D′这3个选项中选择一个作为条件(写序号),并加以证明.
18.(9分)在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(1,3),B(4,1),C(1,1).
(1)画出△ABC关于x轴成轴对称的△A1B1C1;
(2)在网格内以点O为位似中心,使△ABC与△A2B2C2的相似比为1∶2,请画出△A2B2C2.
19.(9分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C,A共线.已知:CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
20.(9分)如图,在△ABC中,D在AC上,DE∥BC,DF∥AB.
(1)求证:△DFC∽△AED;
(2)若CD=AC,求的值.
21.(10分)如图,在 ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由;
(2)连结AC,分别交BE,DF于点G,H,连结BD交AC于点O.若=,AE=4,求BC的长.
22.(10分)如图,矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O,BE与AC相交于点F.
(1)若BE平分∠CBD,求证:BF⊥AC;
(2)找出图中与△OBF相似的三角形,并说明理由;
(3)若OF=3,EF=2,求DE的长度.
23.(11分)(1)某学校“智慧方园”数学社团遇到这样一个题目:如图①,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=3,BO∶CO=1∶3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图②).
请回答:∠ADB=________,AB=________;
(2)请参考以上解决思路,解决问题:如图③,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=3,∠ABC=∠ACB=75°,BO∶OD=1∶3,求DC的长.
答案:
第23章检测题
(时间:100分钟 满分:120分)
1.( C )
2.( C )
3.( D )
4.( B )
5.( C )
6.( B )
7.( A )
8.( C )
9.( B )
10.( A )
11.__6__.
12.__∠ADE=∠B或∠AED=∠C或=(答案不唯一)__,使△ADE∽△ABC.
13.则DF=__10__.
14.__2__.
15.__①②③__(填结论对应的序号).
16.
解:(1)成比例 (2)x=±2
17.
解:③.理由如下:∵△ACD∽△A′C′D′,∴∠ADC=∠A′D′C′,∴∠ADB=∠A′D′B′,又∵∠BAD=∠B′A′D′,∴△ABD∽△A′B′D′.同理,选①也可以.故答案是:③(答案不唯一)
18
解:(1)∵△ABC的三个顶点的坐标分别是A(1,3),B(4,1),C(1,1),∴△ABC关于x轴成轴对称的△A1B1C1的坐标分别为A1(1,-3),B1(4,-1),C1(1,-1),连结A1C1,A1B1,B1C1得到△A1B1C1.如图所示,△A1B1C1即为所求
(2)由题意知:△A2B2C2在△ABC的对侧,则A2(-2,-6),B2(-8,-2),C2(-2,-2),顺次连结各点,得△A2B2C2.如图所示,△A2B2C2即为所求
19.
解:∵BC∥DE,∴△ABC∽△ADE,∴=,∴=,∴AB=17 m,答:河宽AB为17米
20.(9分
解:(1)∵DF∥AB,∴∠CDF=∠A,又∵DE∥BC,∴∠DCF=∠ADE,∴△DFC∽△AED (2)∵CD=AC,∴=,由(1)知△DFC和△AED的相似比为:=,故=()2=()2=
21.
解:(1)四边形BEDF为平行四边形,理由如下:∵四边形ABCD为平行四边形,∴∠ABC=∠ADC,∵∠ABE=∠CDF,∴∠EBF=∠EDF,∵四边形ABCD为平行四边形,∴AD∥BC,∴∠EDF=∠DFC=∠EBF,∴BE∥DF,∵AD∥BC,∴四边形BEDF为平行四边形 (2)设AG=2a,∵=,∴OG=3a,AO=5a,∵四边形ABCD为平行四边形,∴AO=CO=5a,CG=8a,∵AD∥BC,∴△AGE∽△CGB,∴==,∵AE=4,∴BC=16
22.
解:(1)如图,在矩形ABCD中,OD=OC,AB∥CD,∠BCD=90°,∴∠2=∠3=∠4,∠3+∠5=90°,∵DE=BE,∴∠1=∠2,又∵BE平分∠DBC,∴∠1=∠6,∴∠3=∠6,∴∠6+∠5=90°,∴BF⊥AC
(2)与△OBF相似的三角形有△ECF,△BAF.理由如下:∵DE=BE,∴∠1=∠2,又∵∠2=∠3.∴∠1=∠3,∵∠EFC=∠BFO,∴△ECF∽△OBF,∵DE=BE,∴∠1=∠2,又∵∠2=∠4,∴∠1=∠4,又∵∠BFA=∠OFB,∴△BAF∽△OBF
(3)由(2)知△OBF∽△ECF.∴=,∴=,即3CF=2BF,∵OA=OC,∴3OA=3CF+3OF,即3OA=2BF+9①,由(2)知△BAF∽△OBF,∴=,∴BF2=OF·AF,∴BF2=3(OA+3)②,联立①②,可得BF=1+或BF=1-(舍去),∴DE=BE=EF+BF=2+1+=3+
23.
解:(1)∵BD∥AC,∴∠ADB=∠OAC=75°.∵∠BOD=∠COA,∴△BOD∽△COA,∴==.又∵AO=3,∴OD=AO=,∴AD=AO+OD=4.∵∠BAD=30°,∠ADB=75°,∴∠ABD=180°-∠BAD-∠ADB=75°=∠ADB,∴AB=AD=4.故答案为:75°;4 (2)如图所示,过点B作BE∥AD交AC于点E,∵AC⊥AD,BE∥AD,∴∠DAC=∠BEA=90°.∵∠AOD=∠EOB,∴△AOD∽△EOB,∴==.∵BO∶OD=1∶3,∴==.∵AO=3,∴EO=,∴AE=4.∵∠ABC=∠ACB=75°,∴∠BAC=30°,AB=AC,∴AB=2BE.在Rt△AEB中,BE2+AE2=AB2,即(4)2+BE2=(2BE)2,解得BE=4,∴AB=AC=8,AD=12.在Rt△CAD中,AC2+AD2=CD2,即82+122=CD2,解得CD=4
