人教版数学八年级上册12.3角的平分线的性质 同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级上册12.3角的平分线的性质 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 205.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-04 11:14:30 | ||
图片预览



文档简介
12.3角的平分线的性质
一、选择题
1.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若PA=4,则PQ的最小值为( )
A. B.2 C.4 D.
2.如图,,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若,则点P到BC的距离是( )
A.10 B.8 C.5 D.2
3.如图,在中,,AD平分∠BAC,于E,则下列结论:①AD平分∠CDE;②;③DE平分∠ADB;④,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,,以点为圆心,小于的长为半径作圆弧,分别交,于,两点,再分别以,为圆心,以大于长为半径作圆弧两条弧交于点,作射线交于点,若,则( )
A. B. C. D.
5.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F.若S△ABC=28,DE=4,AB=8,则AC长是( )
A.8 B.7 C.6 D.5
6.如如图, Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=10cm,AC=6cm,则BE的长度是( )
A. B. C. D.
7.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
8.如图, 中, , 平分 , 于点 , 于点 , ,则 的长为( )
A.3 B.4 C.5 D.6
二、填空题
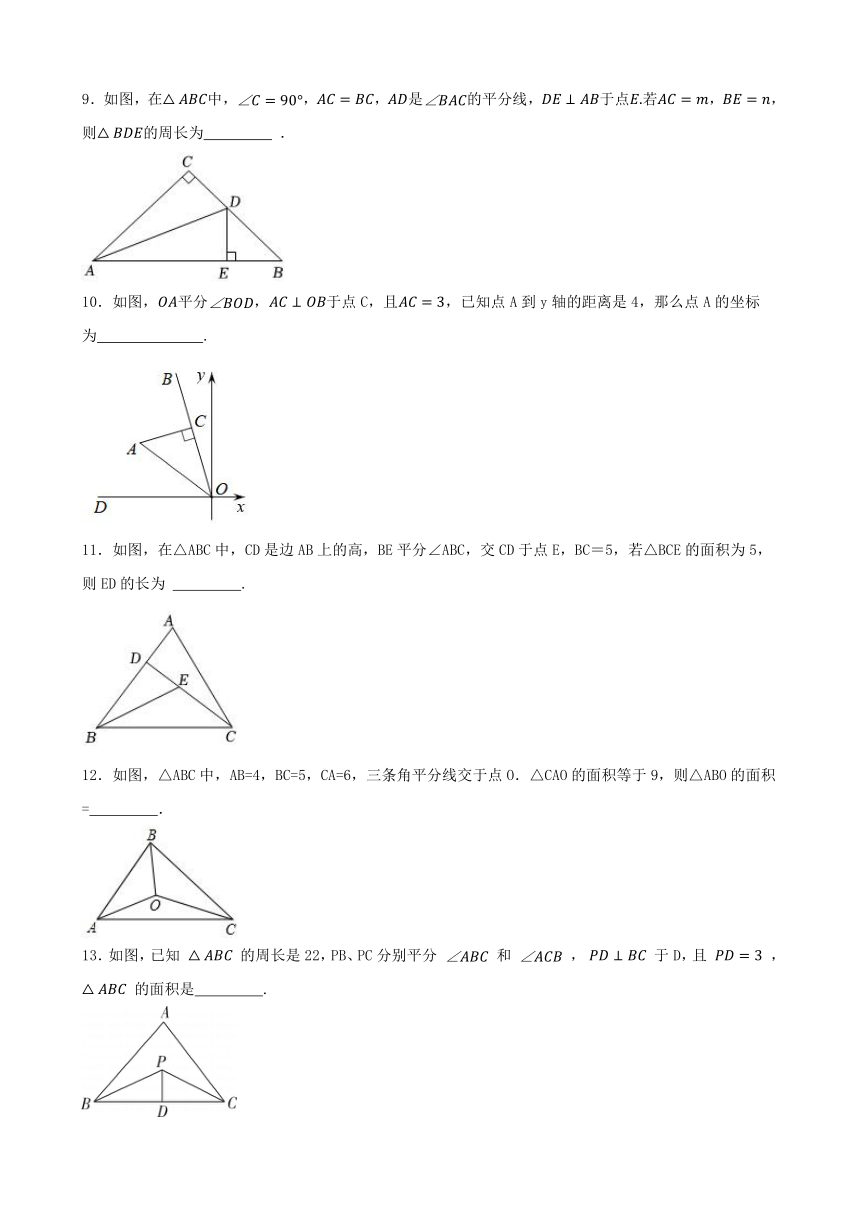
9.如图,在中,,,是的平分线,于点若,,则的周长为 .
10.如图,平分,于点C,且,已知点A到y轴的距离是4,那么点A的坐标为 .
11.如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=5,若△BCE的面积为5,则ED的长为 .
12.如图,△ABC中,AB=4,BC=5,CA=6,三条角平分线交于点O.△CAO的面积等于9,则△ABO的面积= .
13.如图,已知 的周长是22,PB、PC分别平分 和 , 于D,且 , 的面积是 .
三、解答题
14.如图,已知F、G是上两点,M、N是上两点,且,,试问:点P是否在的平分线上?
15.如图,,点O在直线上,平分,,,求的度数.
16.如图,在△ABC中,为的平分线,于点E,于点F,的面积是,求的长.
17.如图,已知△ABC中,∠B=40°,∠C=76°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)若AB=20,AC=16,DE=6,求S△ABC.
18.如图,AD∥BC,∠D=90°.
(1)如图1,若∠DAB的平分线与∠CBA的平分线交于点P,试问:点P是线段CD的中点吗?为什么?
(2)如图2,如果P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数为多少?
参考答案
1.C
2.C
3.C
4.C
5.C
6.B
7.C
8.C
9.m+n
10.(-4,3)
11.2
12.6
13.33
14.解:点P在的平分线上.
理由:过点P分别向,作垂线,
∵,,,,
∴,
∴点P是在的平分线上.
15.解:∵,
∴,
∵平分,
∴,
又∵,
∴.
16.解:为的平分线, ,
,
,
即,
解得:,
.
17.解:(1)∵∠B=40°,∠C=76°,
∴∠BAC=180°﹣40°﹣76°=64°,
∵AD是△ABC的角平分线,
∴,
∵DE⊥AB,
∴∠EDA=90°﹣∠DAE=58°.
(2)过点D作DF⊥AC于点F,
∵AD是△ABC的角平分线,DF⊥AC,DE⊥AB,
∴DF=DE=6,
∴.
18.解:(1)点P是线段CD的中点.理由如下:
过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°﹣∠D=90°,即PC⊥BC,
∵∠DAB的平分线与∠CBA的平分线交于点P,
∴PD=PE,PC=PE,
∴PC=PD,
∴点P是线段CD的中点;
(2)过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°﹣∠D=90°,即PC⊥BC.
在△PBE与△PBC中,
,
∴△PBE≌△PBC(AAS),
∴∠EPB=∠CPB=35°,PE=PC,
∵PC=PD,
∴PD=PE,
在Rt△PAD与Rt△PAE中,
,
∴Rt△PAD≌Rt△PAE(HL),
∴∠APD=∠APE,
∵∠APD+∠APE=180°﹣2×35°=110°,
∴∠APD=55°,
∴∠PAD=90°﹣∠APD=35°.
一、选择题
1.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若PA=4,则PQ的最小值为( )
A. B.2 C.4 D.
2.如图,,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若,则点P到BC的距离是( )
A.10 B.8 C.5 D.2
3.如图,在中,,AD平分∠BAC,于E,则下列结论:①AD平分∠CDE;②;③DE平分∠ADB;④,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图,,以点为圆心,小于的长为半径作圆弧,分别交,于,两点,再分别以,为圆心,以大于长为半径作圆弧两条弧交于点,作射线交于点,若,则( )
A. B. C. D.
5.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F.若S△ABC=28,DE=4,AB=8,则AC长是( )
A.8 B.7 C.6 D.5
6.如如图, Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=10cm,AC=6cm,则BE的长度是( )
A. B. C. D.
7.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
8.如图, 中, , 平分 , 于点 , 于点 , ,则 的长为( )
A.3 B.4 C.5 D.6
二、填空题
9.如图,在中,,,是的平分线,于点若,,则的周长为 .
10.如图,平分,于点C,且,已知点A到y轴的距离是4,那么点A的坐标为 .
11.如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=5,若△BCE的面积为5,则ED的长为 .
12.如图,△ABC中,AB=4,BC=5,CA=6,三条角平分线交于点O.△CAO的面积等于9,则△ABO的面积= .
13.如图,已知 的周长是22,PB、PC分别平分 和 , 于D,且 , 的面积是 .
三、解答题
14.如图,已知F、G是上两点,M、N是上两点,且,,试问:点P是否在的平分线上?
15.如图,,点O在直线上,平分,,,求的度数.
16.如图,在△ABC中,为的平分线,于点E,于点F,的面积是,求的长.
17.如图,已知△ABC中,∠B=40°,∠C=76°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)若AB=20,AC=16,DE=6,求S△ABC.
18.如图,AD∥BC,∠D=90°.
(1)如图1,若∠DAB的平分线与∠CBA的平分线交于点P,试问:点P是线段CD的中点吗?为什么?
(2)如图2,如果P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数为多少?
参考答案
1.C
2.C
3.C
4.C
5.C
6.B
7.C
8.C
9.m+n
10.(-4,3)
11.2
12.6
13.33
14.解:点P在的平分线上.
理由:过点P分别向,作垂线,
∵,,,,
∴,
∴点P是在的平分线上.
15.解:∵,
∴,
∵平分,
∴,
又∵,
∴.
16.解:为的平分线, ,
,
,
即,
解得:,
.
17.解:(1)∵∠B=40°,∠C=76°,
∴∠BAC=180°﹣40°﹣76°=64°,
∵AD是△ABC的角平分线,
∴,
∵DE⊥AB,
∴∠EDA=90°﹣∠DAE=58°.
(2)过点D作DF⊥AC于点F,
∵AD是△ABC的角平分线,DF⊥AC,DE⊥AB,
∴DF=DE=6,
∴.
18.解:(1)点P是线段CD的中点.理由如下:
过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°﹣∠D=90°,即PC⊥BC,
∵∠DAB的平分线与∠CBA的平分线交于点P,
∴PD=PE,PC=PE,
∴PC=PD,
∴点P是线段CD的中点;
(2)过点P作PE⊥AB于E,
∵AD∥BC,∠D=90°,
∴∠C=180°﹣∠D=90°,即PC⊥BC.
在△PBE与△PBC中,
,
∴△PBE≌△PBC(AAS),
∴∠EPB=∠CPB=35°,PE=PC,
∵PC=PD,
∴PD=PE,
在Rt△PAD与Rt△PAE中,
,
∴Rt△PAD≌Rt△PAE(HL),
∴∠APD=∠APE,
∵∠APD+∠APE=180°﹣2×35°=110°,
∴∠APD=55°,
∴∠PAD=90°﹣∠APD=35°.
