导数及其应用

课件47张PPT。普通高中课程标准实验教科书（A版）
选修1-1，2-2
导数及其应用
简 介
人民教育出版社中学数学室 李龙才一、内容结构
二、教学目标
三、对一些关键问题的处理
四、几个需要注意的问题
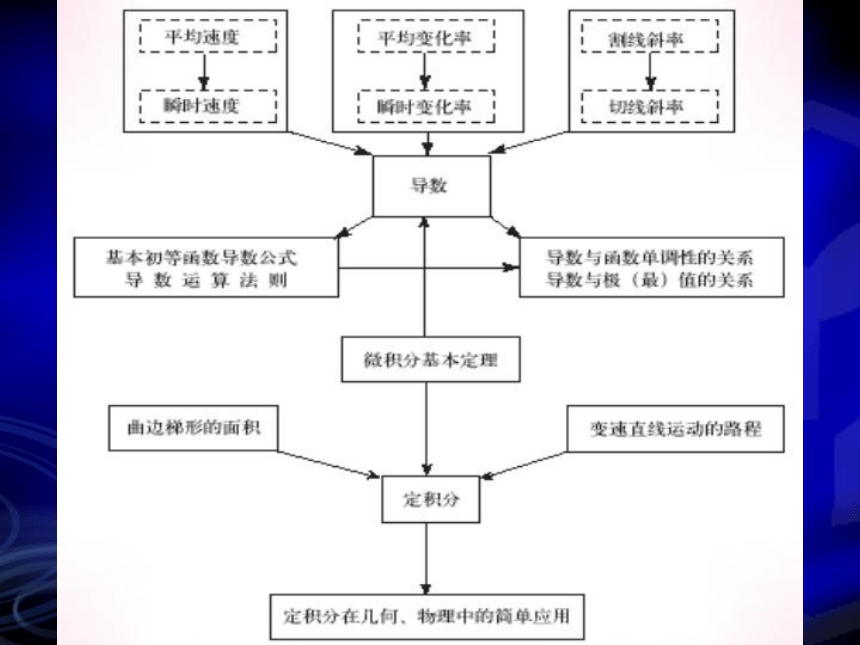
一、内容结构
导数和定积分都是微积分的核心概念，它们
有极其丰富的背景和广泛的应用。本章通过大量
实例，引导学生经历由平均变化率到瞬时变化率
刻画现实问题的过程，体会导数的思想，理解
导数的含义。通过用导数研究函数的单调性、极
值等性质和解决各种最优化问题，体会导数在解
决数学问题和实际问题中的广泛应用和强大力量。
本章还初步介绍定积分的概念及其简单的应用，
学生也将初步体会定积分的思想及其丰富内涵，
为进一步学习微积分打下基础.此外，通过对微
积分发展史的渗透和介绍，使学生体会微积分在
人类思想、文化发展史上的价值。
文科（16课时）：
3.1 变化率与导数 约4课时
3.2 导数的计算 约3课时
3.3 导数在研究函数中的应用 约3课时
3.4 生活中的优化问题举例 约4课时
实习作业 约1课时
小结 约1课时
理科(24课时)：
1.1 变化率与导数 约4课时
1.2 导数的计算 约4课时
1.3 导数在研究函数中的应用 约3课时
1.4 生活中的优化问题举例 约4课时
1.5 定积分的概念 约4课时
1.6 微积分基本定理 约2课时
1.7 定积分的简单应用 约2课时
小结 约1课时二、教学目标(1)体会导数的思想及其内涵
通过分析实例，经历由平均变化率过渡到瞬时变化率的过程，了解导数概念的实际背景，知道瞬时变化率就是导数。
(2)通过函数图象直观地理解导数的几何意义。
2. 能根据导数定义，求 函数

的导数，能利用基本初等函数的导数公式和导
数的四则运算法则求简单函数的导数，能求简
单的复合函数（仅限于形如f(ax+b)）的导数。
3. (1)结合实例，借助几何直观探索并了解函数的单调性与导数的关系；能利用导数研究函数的单调性，会求不超过三次的多项式函数的单调区间。
(2)结合函数的图象，了解函数在某点取得极值的必要条件和充分条件；会用导数求不超多三次的多项式函数的极大值、极小值，以及在给定区间上不超多三次的多项式函数的最大值、最小值。
4.通过使利润最大、用料最省、效率最高等优化问题，体会导数在解决实际问题中的作用。
5.从问题情景中了解定积分的实际背景；借助几何直观体会定积分的基本思想，初步了解定积分的概念．
6. 通过实例（变速运动物体在某段时间内的速度与路程的关系），直观了解微积分基本定理的含义，并能利用微积分基本定理计算简单的定积分．应用定积分解决一些简单的几何和物理问题． 三.对一些关键问题的处理
1.导数概念的引入
反复通过大量实例，引导同学们经历由平均变化率到瞬时变化率刻画现实问题的过程，引入导数的概念，体会导数的思想，理解导数的含义：
气球平均膨胀率；
高台跳水的平均速度 瞬时速度；
函数的平均变化率 瞬时变化率;(定义)
曲线的割线斜率 切线斜率。
（几何意义）
高台跳水问题（一以贯之）
运动员相对于水面的高度h(单位：米)与起跳后的时间t（单位：秒）存在函数关系
h(t)=-4.9t2+6.5t+10.
（1）用运动员在某些时间段内的平均速度粗略地描述其运动状态；
（2）探究运动员在时间段 内的运动状态
平均速度不能反映他在这段时间里运动状态，需要用瞬时速度描述运动状态。
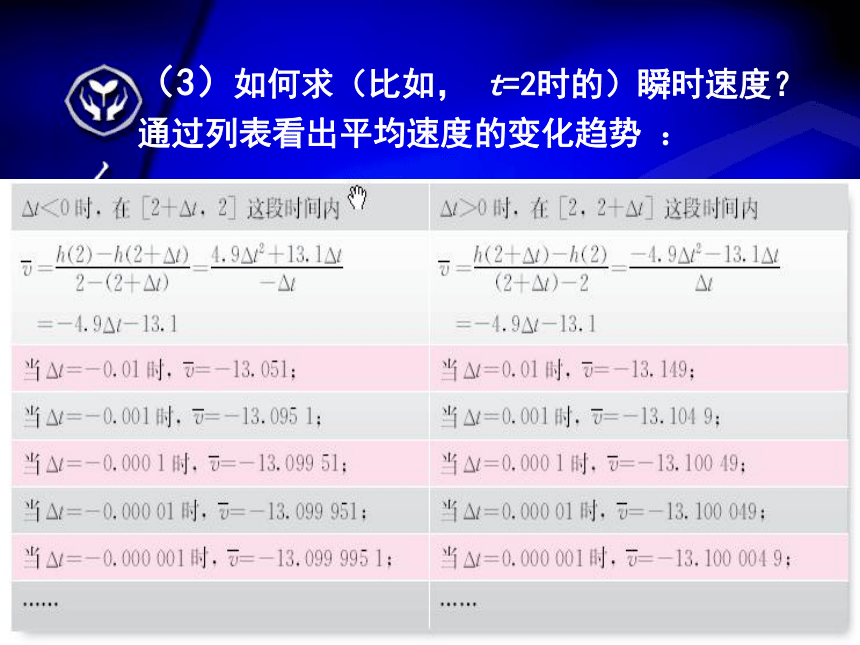
（3）如何求（比如， t=2时的）瞬时速度？
通过列表看出平均速度的变化趋势?：
从平均速度 过渡到瞬时速度

，得到瞬时速度 的值为-13.1 .
从数学上来看，这个过程能够说明变化趋势，也是学生容易理解的，不追求严格的证明。 一般化：从函数的平均变化率到瞬时变化率。
2.导数的几何意义 通过观察曲线y=f(x)在点P(x0,f(x0))处的割线PPn的变化趋势，既获得切线定义，又得到割线PPn的斜率与切线PT的斜率k之间的关系：函数的平均变化率到瞬时变化率。将切线斜率和导数相联系，得到导数的几何意义。
关注用导数本质及其几何意义解决问题 3.导数的计算
（1）给出几个简单函数的导数的推导过程:

并给出前3个结果的几何意义和物理意义。
直接给出基本初等函数的导数公式（其余公式不作推导）；直接给出导数运算法则，不作推导。应用它们求一些简单函数的导数。
（2）避免过度的形式化运算，教科书给出了一些应用导数解决实际问题的例题。
（3）直接给出复合函数的求导公式，不作推导，且只要求利用公式求形如y=f(ax+b)的复合函数的导数。 4.导数的应用导数在研究函数中的应用
（1）函数的单调性——先研究跳水运动，进而从若干个函数的几何图形上，利用导数的几何意义，观察、分析单调性与导函数符号之间的关系，总结出一般规律，并用来解决函数单调性（包括实际问题），求一些简单函数的单调区间。
应用导数探索函数的单调性、极值等性质及其在实际中的应用，感受导数在解决数学问题和实际问题中的作用。
（2）函数的极值——利用单调性，从函数的几何图形上观察、探究极值与导数之间的关系，总结出一般规律 （呈现方式与研究函数单调性类似） ，并用来求一些简单函数极值。
（3）函数的最大（小）值——利用极值，从函数的几何图形上观察、探究最大（小）值与极值、两个端点处的函数值之间的关系，总结出一般规律，并用来求一些简单（连续）函数的最大（小）值（其中多项式函数的次数不超过3次）。
导数方法的一般性和有效性
在解决具体问题的过程中，将研究函数的导数方法与初等方法作比较，体会导数方法在研究函数性质中的一般性和有效性。生活中的优化问题举例
生活中经常遇到求利润最大、用料最省、效率最高等问题，这些问题通常称为优化问题，它们都可以化归为求函数最大（小）值。
两个目的
（1）培养应用意识。运用导数，解决生活中的一些优化问题；
（2）培养学生数学建模的思想：
优化问题 用函数表示的数学问题

优化问题的答案 用导数解决数学问题
5. 定积分概念的引入
着重揭示定积分的思想方法和求解问题的一般步骤
（1）通过解决曲边梯形的面积、变速直线运动的路程这两个典型问题，着重揭示出定积分的思想方法：在每个局部小范围内“以直代曲”
“以不变代变 ”和逼近的思想．事实上，这就是定积分概念中蕴涵的最本质思想，这也是应用定积分解决实际问题的思想方法．
（2）给出求解这类问题的一般步骤——“四步曲” ：分割、近似代替、求和、取极限．
曲边梯形的面积
问题的引出
如何求由抛物线y=x2与直线x=1,y=0,所围成的平面图形部分的面积S？
解决问题的关键（思想方法）
通过回顾求一种特殊的曲边形——圆的面积的过程，通过类比启发学生得到解决问题的思想方法——局部小范围内“以直代曲”“以不变代变 ”和逼近的思想．
解决问题的“四步曲”第一步——分割
把区间[0,1]等分成n个小区间，原来的曲边梯形就被分成n个小曲边梯形．
第二步——近似代替
在每个小区间上进行近似代替， “以
直代曲”，求出每个小曲边梯形面积
的近似值（用左段点处的函数值）．
第三步——求和
求出所有这些近似值的和，就得到原来的曲边梯形面积的近似值．
第四步——取极限
对曲边梯形面积的近似值取极限得到曲边梯形的面积．
通过教科书中的图可以看出，随着分割越来越细，近似值不断趋向于曲边梯形的面积． 教科书中给出的表可以使学生能够定量地看出，随着区间等分数n的增大，曲边梯形的面积趋向于常数 ．
设置“探究”栏目，先用右段点处的函数值进行近似代替，求出曲边梯形的面积，再借助几何直观（可利用信息技术手段）得出面积的一般表达式：
变速直线运动的路程
类比求曲边梯形面积的过程， 从几何图象与物理意义两方面分析、解决问题。得到结果
后，再从反方向上推断出该路程在数值上等于一个曲边梯形的面积，从而为给出定积分的几何意义作铺垫。



引入定积分概念
定积分的几何意义（由两个引例自然地给出） 探究拓广（正、负的情形可后置）
为利用定积分计算面积奠定基础 5.微积分基本定理
突出微积分基本定理的探究过程（强调物理意义，特别是几何意义——导数），直观地了解微积分基本定理的含义，同时又一次经历了数学知识的发现过程．反映微积分基本定理的基本思想,不给出严格证明。

物体的位移是函数在两个端点处的函数值之差，即
从几何意义上看，由导数的几何意义知
求和得近似值
取极限，由定积分的定义得
进而把所得的结论一般化，给出微积分基本定理
强调微积分基本定理的重要意义
不能仅仅从简便、有效地计算定积分的角度认识微积分基本定理的意义，教师应引导学生认识到，更为重要的是它给出微分（导数）和积分（定积分）之间的内在联系：微积分基本定理揭示了导数和定积分之间的内在联系，同时它也提供了计算定积分的一种有效方法.微积分基本定理是微积分学乃至高等数学中最重要的定理，它的作用怎么说都不为过． 6.定积分的简单应用
定积分在几何中的应用
平面图形面积．在这部分的教学中，应特别注意利用定积分的几何意义，注意借助于图形直观，数形结合．
定积分在物理中的应用
变速直线运动的路程：举例复习变速直线运动的路程；
变力所作的功：利用定积分的思想方法，解决变力作功的问题，对于变力作功的公式，教科书中给出了一个＂探究＂，未给出证明，主要是考虑到重点应放在公式的应用上，而不是在公式的推导上．
在这部分的教学中，应特别注意利用这些问题的物理意义，有时也要注意借助于定积分的几何意义，数形结合解决问题．
四.几个需要注意的问题1.不专门讲极限
从数学逻辑体系上看，导数、定积分概念学习的起点是极限，即从数列的极限，到函数的极限，再到导数、定积分。这种概念建立方式具有严密的逻辑性和系统性，但学生很难理解极限的形式化定义。因此也影响了对导数、定积分本质的理解。
不介绍极限的形式化定义及相关知识，而是用直观形象的方法定义导数、定积分。
（1）通过列表计算、直观地把握函数变化趋势(蕴涵着极限的描述性定义)，学生容易理解；
（2）所涉及到的数列或函数都很简单，学生容易观察出其变化趋势； （3）如果讲极限的?-?定义，就特别抽象，难度急剧增大，加大学生对导数、定积分概念的本质认识的难度。
需在教学中检验！
2.强调本质、几何意义、物理意义
理解导数的本质（含义），从几何直观、物理意义上理解概念，借助几何直观、物理意义分析问题、解决问题。
“数形结合”是学习和研究数学的一种重要的思想方法，借助几何直观可以更好地学习、理解数学概念，并提高应用数学概念解决实际问题的能力
3.强调应用
紧密结合实际问题，把解决实际问题贯穿于内容的始终（概念、计算、应用）。
避免过度的形式化运算防止将导数、定积分仅仅作为一些规则和步骤来学习
4.控制难度
控制导数、定积分计算的难度，严格控制定积分应用的广度和难度。