第11章 三角形 单元练习卷(含解析)2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 第11章 三角形 单元练习卷(含解析)2023-2024学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-03 00:00:00 | ||
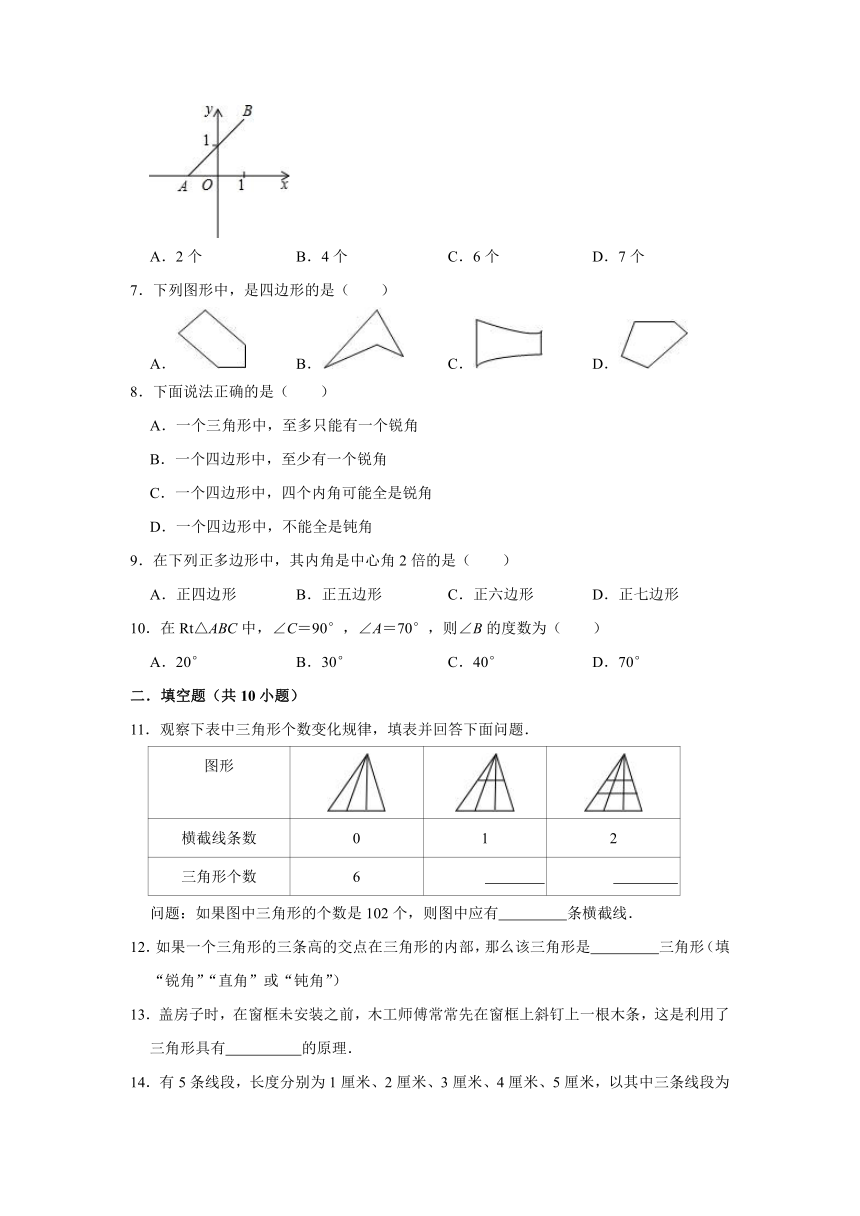
图片预览




文档简介
人教新版八年级上学期《第11章 三角形》
一.选择题(共10小题)
1.下列说法正确的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.面积相等的两个三角形全等
C.有一个角是30°的两个等腰三角形全等
D.斜边和直角边对应相等的两个直角三角形全等
2.如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,垂足分别为D、E.下面有四种结论:①DE是△BCD的高;②DE是△ABE的高;③CD是△ABC的高;④AC是△ABE的高.其中,正确的结论是( )
A.①和③ B.②和③ C.①②③ D.①③④
3.下列长度的三条线段能组成三角形的是( )
A.1,1,2 B.1,2,4 C.2,3,4 D.2,3,5
4.适合条件∠A:∠B:∠C=2:3:5的△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
5.如图,把一副三角板的两个直角三角形叠放在一起,则α的度数( )
A.75° B.135° C.120° D.105°
6.如图,已知点A(﹣1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P共有( )
A.2个 B.4个 C.6个 D.7个
7.下列图形中,是四边形的是( )
A. B. C. D.
8.下面说法正确的是( )
A.一个三角形中,至多只能有一个锐角
B.一个四边形中,至少有一个锐角
C.一个四边形中,四个内角可能全是锐角
D.一个四边形中,不能全是钝角
9.在下列正多边形中,其内角是中心角2倍的是( )
A.正四边形 B.正五边形 C.正六边形 D.正七边形
10.在Rt△ABC中,∠C=90°,∠A=70°,则∠B的度数为( )
A.20° B.30° C.40° D.70°
二.填空题(共10小题)
11.观察下表中三角形个数变化规律,填表并回答下面问题.
图形
横截线条数 0 1 2
三角形个数 6
问题:如果图中三角形的个数是102个,则图中应有 条横截线.
12.如果一个三角形的三条高的交点在三角形的内部,那么该三角形是 三角形(填“锐角”“直角”或“钝角”)
13.盖房子时,在窗框未安装之前,木工师傅常常先在窗框上斜钉上一根木条,这是利用了三角形具有 的原理.
14.有5条线段,长度分别为1厘米、2厘米、3厘米、4厘米、5厘米,以其中三条线段为边长,共可以组成 个形状不同的三角形.
15.如图,∠1= .
16.如图,在直角三角形纸片ABC中,∠A=90°,剪去这个直角后得到一个四边形,则∠BEF+∠CFE的度数是 度.
17.折叠式防盗窗利用的是四边形的 性.
18.如果一个正多边形的一个内角是162°,则这个正多边形是正 边形.
19.一只蚂蚁从A点出发向前走5cm,向左转45°,继续走5cm,再左转45°,它以同样的走法第一次走回A点时,共走了 cm
20.如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是 .
三.解答题(共5小题)
21.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长.
22.AD是△ABC的中线,AB=10,AC=7,△ABD的周长比△ACD的周长大多少?
23.如图,在△ABC中,∠B=40°,∠BCD=100°,CE平分∠ACB.
求∠A和∠BEC的度数.
24.如图,在凹四边形ABCD中,∠A=45°,∠B=55°,∠D=20°,求∠BCD的度数.
下面是学习小组的同学们交流时得到的解决问题的三种方法:
方法一:作射线AC;
方法二:延长BC交AD于点E;
方法三:连接BD.
请选择上述一种方法,求∠BCD的度数.
25.如图所示,在四边形ABCD中,AB∥DC,点P为BC上一点,设∠CDP=α,∠DPC=β,当点P在边BC上(不包括点C)运动时,α,β与∠B有什么关系?
人教新版八年级上学期《第11章 三角形》
参考答案与试题解析
一.选择题(共10小题)
1.下列说法正确的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.面积相等的两个三角形全等
C.有一个角是30°的两个等腰三角形全等
D.斜边和直角边对应相等的两个直角三角形全等
【考点】全等三角形的判定.
【答案】D
【分析】A、画出图形(反例),判断A即可;画出反例图形,即可判断B;根据顶角是30°或底角是30°,即可判断C;根据直角三角形的全等的判定定理HL,即可判断D.
【解答】解:A、如图:
AC=CD,BC=BC,∠B=∠B,但△BDC和△ABC不全等,故本选项错误;
B、△ABC的面积是×2×1=1,△EFG的面积是×1×2=1,但△ABC和△EFG不全等,故本选项错误;
C、当一个是底角是30°,而另一个是顶角是30°时,两等腰三角形不全等,故本选项错误;
D、根据HL即可得出结论,故本选项正确;
故选:D.
2.如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,垂足分别为D、E.下面有四种结论:①DE是△BCD的高;②DE是△ABE的高;③CD是△ABC的高;④AC是△ABE的高.其中,正确的结论是( )
A.①和③ B.②和③ C.①②③ D.①③④
【考点】三角形的角平分线、中线和高.
【答案】D
【分析】根据高的概念可知.
【解答】解:①DE是△BCD的高,正确;
②AC是△ABE的高,错误;
③CD是△ABC的高,正确;
④AC是△ABE的高,正确;
故选:D.
3.下列长度的三条线段能组成三角形的是( )
A.1,1,2 B.1,2,4 C.2,3,4 D.2,3,5
【考点】三角形三边关系.
【答案】C
【分析】根据三角形的三边关系进行分析判断.
【解答】解:根据三角形任意两边的和大于第三边,得
A中,1+1=2,不能组成三角形;
B中,1+2=3<4,不能够组成三角形;
C中,2+3=5>4,能组成三角形;
D中,2+3=5,不能组成三角形.
故选:C.
4.适合条件∠A:∠B:∠C=2:3:5的△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
【考点】三角形内角和定理.
【答案】B
【分析】设∠A为2x,得出∠B为3x,∠C为5x,根据三角形的内角和为180°,求出各角的度数,即可得出答案.
【解答】解:设∠A为2x,则∠B为3x,∠C为4x,根据题意得:
2x+3x+5x=180°,
解得;x=18,
则∠A=36°,∠B=54°,∠C=90°,
适合条件∠A:∠B:∠C=2:3:5的三角形ABC是直角三角形;
故选:B.
5.如图,把一副三角板的两个直角三角形叠放在一起,则α的度数( )
A.75° B.135° C.120° D.105°
【考点】三角形的外角性质.
【答案】D
【分析】先根据三角板的性质得出∠1及∠2的度数,再由三角形内角和定理即可得出结论.
【解答】解:∵图中是一副直角三角板,
∴∠1=45°,∠2=30°,
∴∠α=180°﹣45°﹣30°=105°.
故选:D.
6.如图,已知点A(﹣1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P共有( )
A.2个 B.4个 C.6个 D.7个
【考点】直角三角形的性质;坐标与图形性质.
【答案】C
【分析】当∠PBA=90°时,即点P的位置有2个;当∠BPA=90°时,点P的位置有3个;当∠BAP=90°时,在y轴上共有1个交点.
【解答】解:①以A为直角顶点,可过A作直线垂直于AB,与坐标轴交于一点,这一点符合点P的要求;
②以B为直角顶点,可过B作直线垂直于AB,与坐标轴交于两点,这两点也符合P点的要求;
③以P为直角顶点,可以AB为直径画圆,与坐标轴共有3个交点.
所以满足条件的点P共有6个.
故选:C.
7.下列图形中,是四边形的是( )
A. B. C. D.
【考点】多边形.
【答案】B
【分析】根据四边形的定义,由四条线段首尾顺次连接而成的图形是四边形,再结合图形进行判断即可.
【解答】解:A、D的图形都由5条线段组成,是五边形;
C、围成图形的不都是线段,所以不是四边形;
只有B选项符合四边形的定义.
故选:B.
8.下面说法正确的是( )
A.一个三角形中,至多只能有一个锐角
B.一个四边形中,至少有一个锐角
C.一个四边形中,四个内角可能全是锐角
D.一个四边形中,不能全是钝角
【考点】多边形内角与外角;三角形内角和定理.
【答案】D
【分析】根据多边形的内角和定理分别可以判定那个正确.
【解答】解:A、不对,例如:90,45,45;
B、不对,例如:90,90,90,90;
C、不对,四个角都是锐角那么不能满足内角和360°;
D、正确.
故选:D.
9.在下列正多边形中,其内角是中心角2倍的是( )
A.正四边形 B.正五边形 C.正六边形 D.正七边形
【考点】多边形内角与外角.
【答案】C
【分析】正n边形的内角和是(n﹣2) 180°,则内角就可表示出,中心角是.根据内角是中心角2倍就可列方程求出边数.
【解答】解:设多边形的边数是n.
则每个内角是,中心角是.
根据题意得:=2×
解得:n=6.
故选:C.
10.在Rt△ABC中,∠C=90°,∠A=70°,则∠B的度数为( )
A.20° B.30° C.40° D.70°
【考点】直角三角形的性质.
【答案】A
【分析】由直角三角形的性质可直接求得答案.
【解答】解:
∵在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°,
∴∠B=90°﹣∠A=90°﹣70°=20°,
故选:A.
二.填空题(共10小题)
11.观察下表中三角形个数变化规律,填表并回答下面问题.
图形
横截线条数 0 1 2
三角形个数 6 12 18
问题:如果图中三角形的个数是102个,则图中应有 16 条横截线.
【考点】三角形.
【答案】见试题解答内容
【分析】观察图形,不难发现:当横线是0条的时候,有6个三角形;当横线是1条的时候有6+6=12个三角形,即多一条横线,多6个三角形;所以当有n条横线的时候,有(6+6n)个三角形.根据这一规律,得当有1条横线时,有12个三角形;当有2条横线时,有18个三角形;当有102个三角形的时候,即6+6n=102,n=16.
【解答】解:表格中应是12,18;
有n条横线的时候,有(6+6n)个三角形,
∴6+6n=102,n=16,有16条横线.
故答案为:12,18;16.
12.如果一个三角形的三条高的交点在三角形的内部,那么该三角形是 锐角 三角形(填“锐角”“直角”或“钝角”)
【考点】三角形的角平分线、中线和高.
【答案】见试题解答内容
【分析】根据三角形高的定义知,若三角形的两条高都在三角形的内部,则此三角形是锐角三角形.
【解答】解:利用三角形高线的位置关系得出:如果一个三角形两边上的高的交点在三角形的内部,
那么这个三角形是锐角三角形.
故答案为:锐角.
13.盖房子时,在窗框未安装之前,木工师傅常常先在窗框上斜钉上一根木条,这是利用了三角形具有 稳定性 的原理.
【考点】三角形的稳定性.
【答案】见试题解答内容
【分析】在窗框上斜钉一根木条,构成三角形,故可用三角形的稳定性解释.
【解答】解:盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样就构成了三角形,故这样做的数学道理是三角形的稳定性.
故答案为:稳定性.
14.有5条线段,长度分别为1厘米、2厘米、3厘米、4厘米、5厘米,以其中三条线段为边长,共可以组成 3 个形状不同的三角形.
【考点】三角形三边关系.
【答案】见试题解答内容
【分析】先以任意三条线段为一组分组,再根据三角形的任意两边之和大于第三边,任意两边之差小于第三边判断能否组成三角形.
【解答】解:任取三条线段为一组得:①1、2、3,②1、2、4,③1、2、5,④1、3、4,⑤1、3、5,⑥1、4、5,⑦2、3、4,⑧2、3、5,⑨2、4、5,⑩3、4、5,共十组,
①∵1+2=3,∴不能组成三角形;
②∵1+2=3<4,∴不能组成三角形;
③∵1+2=3<5,∴不能组成三角形;
④∵1+3=4,∴不能组成三角形;
⑤∵1+3=4<5,∴不能组成三角形;
⑥∵1+4=5,∴不能组成三角形;
⑦能够组成三角形;
⑧∵2+3=5,∴不能组成三角形;
⑨能够组成三角形;
⑩能够组成三角形.
故共可以组成3个形状不同的三角形.
15.如图,∠1= 140° .
【考点】三角形的外角性质.
【答案】见试题解答内容
【分析】根据三角形的一个外角等于和它不相邻的两个内角的和计算即可.
【解答】解:由三角形的外角的性质可知,∠1=60°+80°=140°,
故答案为:140°.
16.如图,在直角三角形纸片ABC中,∠A=90°,剪去这个直角后得到一个四边形,则∠BEF+∠CFE的度数是 270 度.
【考点】直角三角形的性质.
【答案】见试题解答内容
【分析】先根据直角三角形的性质求得两个锐角和是90度,再根据四边形的内角和是360度,即可求得∠BEF+∠CFE的值.
【解答】解:∵∠A=90°,
∴∠B+∠C=90°.
∵∠B+∠C+∠BEF+∠CFE=360°,
∴∠BEF+∠CFE=360°﹣90°=270°.
故答案为270.
17.折叠式防盗窗利用的是四边形的 不稳定 性.
【考点】多边形.
【答案】见试题解答内容
【分析】一个四边形的四边确定,但它的形状大小仍会发生改变,这叫四边形的不稳定性.显然这是运用了四边形的不稳定性.
【解答】解:折叠式防盗窗利用的是四边形的不稳定性.
18.如果一个正多边形的一个内角是162°,则这个正多边形是正 二十 边形.
【考点】多边形内角与外角.
【答案】二十.
【分析】首先根据求出外角度数,再利用外角和定理求出边数.
【解答】解:∵正多边形的一个内角是162°,
∴它的外角是:180°﹣162°=18°,
边数n=360°÷18°=20.
故答案为:二十.
19.一只蚂蚁从A点出发向前走5cm,向左转45°,继续走5cm,再左转45°,它以同样的走法第一次走回A点时,共走了 40 cm
【考点】多边形内角与外角.
【答案】见试题解答内容
【分析】本题首先要理解题意,这只蚂蚁所走的路程正好是一个外角为45°的多边形的周长,进而求出多边形的周长即可.
【解答】解:∵由题意可知它所走的路程正好是一个外角为45°的多边形的周长,
∴由360°÷45°=8,则此多边形为八边形,
∵由题意可知它的边长为5cm,
∴此八边形的周长为40cm,即它共走了40cm.
20.如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是 100° .
【考点】多边形内角与外角;三角形内角和定理.
【答案】见试题解答内容
【分析】首先根据四边形内角和可得∠ADC+∠DCB=360°﹣200°=160°,再根据角平分线的性质可得∠ODC+∠OCD=×160°=80°,再进一步利用三角形内角和定理可得答案.
【解答】解:∵四边形ABCD中,∠A+∠B=200°,
∴∠ADC+∠DCB=360°﹣200°=160°,
∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=∠ADC,∠OCD=BCD,
∴∠ODC+∠OCD=×160°=80°,
∴∠COD=180°﹣80°=100°,
故答案为:100°.
三.解答题(共5小题)
21.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长.
【考点】三角形的角平分线、中线和高.
【答案】见试题解答内容
【分析】(1)由等量代换可得到∠B+∠BCD=90°,故△BDC是直角三角形,即CD⊥AB;
(2)由面积法可求得CD的长.
【解答】解:(1)∵∠1+∠BCD=90°,∠1=∠B
∴∠B+∠BCD=90°
∴△BDC是直角三角形,即CD⊥AB,
∴CD是△ABC的高;
(2)∵∠ACB=∠CDB=90°
∴S△ABC=AC BC=AB CD,
∵AC=8,BC=6,AB=10,
∴CD===.
22.AD是△ABC的中线,AB=10,AC=7,△ABD的周长比△ACD的周长大多少?
【考点】三角形的角平分线、中线和高.
【答案】见试题解答内容
【分析】根据三角形的周长的计算方法得到△ABD的周长和△ADC的周长的差就是AB与AC的差.
【解答】解:∵AD是△ABC的中线,
∴BD=DC=BC,
∴△ABD的周长﹣△ADC的周长
=(AB+BD+AD)﹣(AC+DC+AD)
=(AB+BC+AD)﹣(AC+BC+AD)
=AB﹣AC
=10﹣7
=3,
故△ABD的周长比△ACD的周长大3.
23.如图,在△ABC中,∠B=40°,∠BCD=100°,CE平分∠ACB.
求∠A和∠BEC的度数.
【考点】三角形内角和定理;三角形的外角性质.
【答案】见试题解答内容
【分析】由∠B=40°,∠BCD=100°,根据三角形外角的性质可得到∠A=∠BCD﹣∠B=100°﹣40°=60°;再根据邻补角的定义得到∠ACB=180°﹣100°=80°,利用角平分线的定义得到∠BCE=40°,最后根据三角形的内角和定理求出∠BEC的度数.
【解答】解:∵∠B=40°,∠BCD=100°,
∴∠A=∠BCD﹣∠B=100°﹣40°=60°,
又∵∠BCD=100°,
∴∠ACB=180°﹣100°=80°,
而CE平分∠ACB,
∴∠BCE=40°,
∴∠BEC=180°﹣∠B﹣∠BCE=180°﹣40°﹣40°=100°.
故答案为:∠A和∠BEC的度数分别为60°,100°.
24.如图,在凹四边形ABCD中,∠A=45°,∠B=55°,∠D=20°,求∠BCD的度数.
下面是学习小组的同学们交流时得到的解决问题的三种方法:
方法一:作射线AC;
方法二:延长BC交AD于点E;
方法三:连接BD.
请选择上述一种方法,求∠BCD的度数.
【考点】多边形内角与外角.
【答案】∠BCD的度数是120°.
【分析】通过延长BC交AD于点E,运用三角形的外角等于和它不相邻两内角的和进行求解.
【解答】解:延长BC交AD于点E,
∴∠CED=∠A+∠B,∠BCD=∠CED+∠D,
∴∠BCD=∠A+∠B+∠D
=45°+55°+20°
=120°,
即∠BCD的度数是120°.
25.如图所示,在四边形ABCD中,AB∥DC,点P为BC上一点,设∠CDP=α,∠DPC=β,当点P在边BC上(不包括点C)运动时,α,β与∠B有什么关系?
【考点】多边形内角与外角;平行线的性质.
【答案】见试题解答内容
【分析】在△CDP中,先由三角形内角和为180°,得出α+β=180°﹣∠C;再由AB∥CD,根据平行线的性质,得出∠B=180°﹣∠C;从而得出α+β=∠B.
【解答】解:在△CDP中,∵∠CDP+∠CPD+∠C=180°,∠CDP=α,∠CPD=β,
∴α+β=∠CDP+∠CPD=180°﹣∠C;
∵AB∥CD,
∴∠B+∠C=180°,
∴∠B=180°﹣∠C;
∴α+β=∠B.
一.选择题(共10小题)
1.下列说法正确的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.面积相等的两个三角形全等
C.有一个角是30°的两个等腰三角形全等
D.斜边和直角边对应相等的两个直角三角形全等
2.如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,垂足分别为D、E.下面有四种结论:①DE是△BCD的高;②DE是△ABE的高;③CD是△ABC的高;④AC是△ABE的高.其中,正确的结论是( )
A.①和③ B.②和③ C.①②③ D.①③④
3.下列长度的三条线段能组成三角形的是( )
A.1,1,2 B.1,2,4 C.2,3,4 D.2,3,5
4.适合条件∠A:∠B:∠C=2:3:5的△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
5.如图,把一副三角板的两个直角三角形叠放在一起,则α的度数( )
A.75° B.135° C.120° D.105°
6.如图,已知点A(﹣1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P共有( )
A.2个 B.4个 C.6个 D.7个
7.下列图形中,是四边形的是( )
A. B. C. D.
8.下面说法正确的是( )
A.一个三角形中,至多只能有一个锐角
B.一个四边形中,至少有一个锐角
C.一个四边形中,四个内角可能全是锐角
D.一个四边形中,不能全是钝角
9.在下列正多边形中,其内角是中心角2倍的是( )
A.正四边形 B.正五边形 C.正六边形 D.正七边形
10.在Rt△ABC中,∠C=90°,∠A=70°,则∠B的度数为( )
A.20° B.30° C.40° D.70°
二.填空题(共10小题)
11.观察下表中三角形个数变化规律,填表并回答下面问题.
图形
横截线条数 0 1 2
三角形个数 6
问题:如果图中三角形的个数是102个,则图中应有 条横截线.
12.如果一个三角形的三条高的交点在三角形的内部,那么该三角形是 三角形(填“锐角”“直角”或“钝角”)
13.盖房子时,在窗框未安装之前,木工师傅常常先在窗框上斜钉上一根木条,这是利用了三角形具有 的原理.
14.有5条线段,长度分别为1厘米、2厘米、3厘米、4厘米、5厘米,以其中三条线段为边长,共可以组成 个形状不同的三角形.
15.如图,∠1= .
16.如图,在直角三角形纸片ABC中,∠A=90°,剪去这个直角后得到一个四边形,则∠BEF+∠CFE的度数是 度.
17.折叠式防盗窗利用的是四边形的 性.
18.如果一个正多边形的一个内角是162°,则这个正多边形是正 边形.
19.一只蚂蚁从A点出发向前走5cm,向左转45°,继续走5cm,再左转45°,它以同样的走法第一次走回A点时,共走了 cm
20.如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是 .
三.解答题(共5小题)
21.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长.
22.AD是△ABC的中线,AB=10,AC=7,△ABD的周长比△ACD的周长大多少?
23.如图,在△ABC中,∠B=40°,∠BCD=100°,CE平分∠ACB.
求∠A和∠BEC的度数.
24.如图,在凹四边形ABCD中,∠A=45°,∠B=55°,∠D=20°,求∠BCD的度数.
下面是学习小组的同学们交流时得到的解决问题的三种方法:
方法一:作射线AC;
方法二:延长BC交AD于点E;
方法三:连接BD.
请选择上述一种方法,求∠BCD的度数.
25.如图所示,在四边形ABCD中,AB∥DC,点P为BC上一点,设∠CDP=α,∠DPC=β,当点P在边BC上(不包括点C)运动时,α,β与∠B有什么关系?
人教新版八年级上学期《第11章 三角形》
参考答案与试题解析
一.选择题(共10小题)
1.下列说法正确的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.面积相等的两个三角形全等
C.有一个角是30°的两个等腰三角形全等
D.斜边和直角边对应相等的两个直角三角形全等
【考点】全等三角形的判定.
【答案】D
【分析】A、画出图形(反例),判断A即可;画出反例图形,即可判断B;根据顶角是30°或底角是30°,即可判断C;根据直角三角形的全等的判定定理HL,即可判断D.
【解答】解:A、如图:
AC=CD,BC=BC,∠B=∠B,但△BDC和△ABC不全等,故本选项错误;
B、△ABC的面积是×2×1=1,△EFG的面积是×1×2=1,但△ABC和△EFG不全等,故本选项错误;
C、当一个是底角是30°,而另一个是顶角是30°时,两等腰三角形不全等,故本选项错误;
D、根据HL即可得出结论,故本选项正确;
故选:D.
2.如图,在△ABC中,∠ACB=90°,CD⊥AB,DE⊥BC,垂足分别为D、E.下面有四种结论:①DE是△BCD的高;②DE是△ABE的高;③CD是△ABC的高;④AC是△ABE的高.其中,正确的结论是( )
A.①和③ B.②和③ C.①②③ D.①③④
【考点】三角形的角平分线、中线和高.
【答案】D
【分析】根据高的概念可知.
【解答】解:①DE是△BCD的高,正确;
②AC是△ABE的高,错误;
③CD是△ABC的高,正确;
④AC是△ABE的高,正确;
故选:D.
3.下列长度的三条线段能组成三角形的是( )
A.1,1,2 B.1,2,4 C.2,3,4 D.2,3,5
【考点】三角形三边关系.
【答案】C
【分析】根据三角形的三边关系进行分析判断.
【解答】解:根据三角形任意两边的和大于第三边,得
A中,1+1=2,不能组成三角形;
B中,1+2=3<4,不能够组成三角形;
C中,2+3=5>4,能组成三角形;
D中,2+3=5,不能组成三角形.
故选:C.
4.适合条件∠A:∠B:∠C=2:3:5的△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
【考点】三角形内角和定理.
【答案】B
【分析】设∠A为2x,得出∠B为3x,∠C为5x,根据三角形的内角和为180°,求出各角的度数,即可得出答案.
【解答】解:设∠A为2x,则∠B为3x,∠C为4x,根据题意得:
2x+3x+5x=180°,
解得;x=18,
则∠A=36°,∠B=54°,∠C=90°,
适合条件∠A:∠B:∠C=2:3:5的三角形ABC是直角三角形;
故选:B.
5.如图,把一副三角板的两个直角三角形叠放在一起,则α的度数( )
A.75° B.135° C.120° D.105°
【考点】三角形的外角性质.
【答案】D
【分析】先根据三角板的性质得出∠1及∠2的度数,再由三角形内角和定理即可得出结论.
【解答】解:∵图中是一副直角三角板,
∴∠1=45°,∠2=30°,
∴∠α=180°﹣45°﹣30°=105°.
故选:D.
6.如图,已知点A(﹣1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P共有( )
A.2个 B.4个 C.6个 D.7个
【考点】直角三角形的性质;坐标与图形性质.
【答案】C
【分析】当∠PBA=90°时,即点P的位置有2个;当∠BPA=90°时,点P的位置有3个;当∠BAP=90°时,在y轴上共有1个交点.
【解答】解:①以A为直角顶点,可过A作直线垂直于AB,与坐标轴交于一点,这一点符合点P的要求;
②以B为直角顶点,可过B作直线垂直于AB,与坐标轴交于两点,这两点也符合P点的要求;
③以P为直角顶点,可以AB为直径画圆,与坐标轴共有3个交点.
所以满足条件的点P共有6个.
故选:C.
7.下列图形中,是四边形的是( )
A. B. C. D.
【考点】多边形.
【答案】B
【分析】根据四边形的定义,由四条线段首尾顺次连接而成的图形是四边形,再结合图形进行判断即可.
【解答】解:A、D的图形都由5条线段组成,是五边形;
C、围成图形的不都是线段,所以不是四边形;
只有B选项符合四边形的定义.
故选:B.
8.下面说法正确的是( )
A.一个三角形中,至多只能有一个锐角
B.一个四边形中,至少有一个锐角
C.一个四边形中,四个内角可能全是锐角
D.一个四边形中,不能全是钝角
【考点】多边形内角与外角;三角形内角和定理.
【答案】D
【分析】根据多边形的内角和定理分别可以判定那个正确.
【解答】解:A、不对,例如:90,45,45;
B、不对,例如:90,90,90,90;
C、不对,四个角都是锐角那么不能满足内角和360°;
D、正确.
故选:D.
9.在下列正多边形中,其内角是中心角2倍的是( )
A.正四边形 B.正五边形 C.正六边形 D.正七边形
【考点】多边形内角与外角.
【答案】C
【分析】正n边形的内角和是(n﹣2) 180°,则内角就可表示出,中心角是.根据内角是中心角2倍就可列方程求出边数.
【解答】解:设多边形的边数是n.
则每个内角是,中心角是.
根据题意得:=2×
解得:n=6.
故选:C.
10.在Rt△ABC中,∠C=90°,∠A=70°,则∠B的度数为( )
A.20° B.30° C.40° D.70°
【考点】直角三角形的性质.
【答案】A
【分析】由直角三角形的性质可直接求得答案.
【解答】解:
∵在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°,
∴∠B=90°﹣∠A=90°﹣70°=20°,
故选:A.
二.填空题(共10小题)
11.观察下表中三角形个数变化规律,填表并回答下面问题.
图形
横截线条数 0 1 2
三角形个数 6 12 18
问题:如果图中三角形的个数是102个,则图中应有 16 条横截线.
【考点】三角形.
【答案】见试题解答内容
【分析】观察图形,不难发现:当横线是0条的时候,有6个三角形;当横线是1条的时候有6+6=12个三角形,即多一条横线,多6个三角形;所以当有n条横线的时候,有(6+6n)个三角形.根据这一规律,得当有1条横线时,有12个三角形;当有2条横线时,有18个三角形;当有102个三角形的时候,即6+6n=102,n=16.
【解答】解:表格中应是12,18;
有n条横线的时候,有(6+6n)个三角形,
∴6+6n=102,n=16,有16条横线.
故答案为:12,18;16.
12.如果一个三角形的三条高的交点在三角形的内部,那么该三角形是 锐角 三角形(填“锐角”“直角”或“钝角”)
【考点】三角形的角平分线、中线和高.
【答案】见试题解答内容
【分析】根据三角形高的定义知,若三角形的两条高都在三角形的内部,则此三角形是锐角三角形.
【解答】解:利用三角形高线的位置关系得出:如果一个三角形两边上的高的交点在三角形的内部,
那么这个三角形是锐角三角形.
故答案为:锐角.
13.盖房子时,在窗框未安装之前,木工师傅常常先在窗框上斜钉上一根木条,这是利用了三角形具有 稳定性 的原理.
【考点】三角形的稳定性.
【答案】见试题解答内容
【分析】在窗框上斜钉一根木条,构成三角形,故可用三角形的稳定性解释.
【解答】解:盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样就构成了三角形,故这样做的数学道理是三角形的稳定性.
故答案为:稳定性.
14.有5条线段,长度分别为1厘米、2厘米、3厘米、4厘米、5厘米,以其中三条线段为边长,共可以组成 3 个形状不同的三角形.
【考点】三角形三边关系.
【答案】见试题解答内容
【分析】先以任意三条线段为一组分组,再根据三角形的任意两边之和大于第三边,任意两边之差小于第三边判断能否组成三角形.
【解答】解:任取三条线段为一组得:①1、2、3,②1、2、4,③1、2、5,④1、3、4,⑤1、3、5,⑥1、4、5,⑦2、3、4,⑧2、3、5,⑨2、4、5,⑩3、4、5,共十组,
①∵1+2=3,∴不能组成三角形;
②∵1+2=3<4,∴不能组成三角形;
③∵1+2=3<5,∴不能组成三角形;
④∵1+3=4,∴不能组成三角形;
⑤∵1+3=4<5,∴不能组成三角形;
⑥∵1+4=5,∴不能组成三角形;
⑦能够组成三角形;
⑧∵2+3=5,∴不能组成三角形;
⑨能够组成三角形;
⑩能够组成三角形.
故共可以组成3个形状不同的三角形.
15.如图,∠1= 140° .
【考点】三角形的外角性质.
【答案】见试题解答内容
【分析】根据三角形的一个外角等于和它不相邻的两个内角的和计算即可.
【解答】解:由三角形的外角的性质可知,∠1=60°+80°=140°,
故答案为:140°.
16.如图,在直角三角形纸片ABC中,∠A=90°,剪去这个直角后得到一个四边形,则∠BEF+∠CFE的度数是 270 度.
【考点】直角三角形的性质.
【答案】见试题解答内容
【分析】先根据直角三角形的性质求得两个锐角和是90度,再根据四边形的内角和是360度,即可求得∠BEF+∠CFE的值.
【解答】解:∵∠A=90°,
∴∠B+∠C=90°.
∵∠B+∠C+∠BEF+∠CFE=360°,
∴∠BEF+∠CFE=360°﹣90°=270°.
故答案为270.
17.折叠式防盗窗利用的是四边形的 不稳定 性.
【考点】多边形.
【答案】见试题解答内容
【分析】一个四边形的四边确定,但它的形状大小仍会发生改变,这叫四边形的不稳定性.显然这是运用了四边形的不稳定性.
【解答】解:折叠式防盗窗利用的是四边形的不稳定性.
18.如果一个正多边形的一个内角是162°,则这个正多边形是正 二十 边形.
【考点】多边形内角与外角.
【答案】二十.
【分析】首先根据求出外角度数,再利用外角和定理求出边数.
【解答】解:∵正多边形的一个内角是162°,
∴它的外角是:180°﹣162°=18°,
边数n=360°÷18°=20.
故答案为:二十.
19.一只蚂蚁从A点出发向前走5cm,向左转45°,继续走5cm,再左转45°,它以同样的走法第一次走回A点时,共走了 40 cm
【考点】多边形内角与外角.
【答案】见试题解答内容
【分析】本题首先要理解题意,这只蚂蚁所走的路程正好是一个外角为45°的多边形的周长,进而求出多边形的周长即可.
【解答】解:∵由题意可知它所走的路程正好是一个外角为45°的多边形的周长,
∴由360°÷45°=8,则此多边形为八边形,
∵由题意可知它的边长为5cm,
∴此八边形的周长为40cm,即它共走了40cm.
20.如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是 100° .
【考点】多边形内角与外角;三角形内角和定理.
【答案】见试题解答内容
【分析】首先根据四边形内角和可得∠ADC+∠DCB=360°﹣200°=160°,再根据角平分线的性质可得∠ODC+∠OCD=×160°=80°,再进一步利用三角形内角和定理可得答案.
【解答】解:∵四边形ABCD中,∠A+∠B=200°,
∴∠ADC+∠DCB=360°﹣200°=160°,
∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=∠ADC,∠OCD=BCD,
∴∠ODC+∠OCD=×160°=80°,
∴∠COD=180°﹣80°=100°,
故答案为:100°.
三.解答题(共5小题)
21.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长.
【考点】三角形的角平分线、中线和高.
【答案】见试题解答内容
【分析】(1)由等量代换可得到∠B+∠BCD=90°,故△BDC是直角三角形,即CD⊥AB;
(2)由面积法可求得CD的长.
【解答】解:(1)∵∠1+∠BCD=90°,∠1=∠B
∴∠B+∠BCD=90°
∴△BDC是直角三角形,即CD⊥AB,
∴CD是△ABC的高;
(2)∵∠ACB=∠CDB=90°
∴S△ABC=AC BC=AB CD,
∵AC=8,BC=6,AB=10,
∴CD===.
22.AD是△ABC的中线,AB=10,AC=7,△ABD的周长比△ACD的周长大多少?
【考点】三角形的角平分线、中线和高.
【答案】见试题解答内容
【分析】根据三角形的周长的计算方法得到△ABD的周长和△ADC的周长的差就是AB与AC的差.
【解答】解:∵AD是△ABC的中线,
∴BD=DC=BC,
∴△ABD的周长﹣△ADC的周长
=(AB+BD+AD)﹣(AC+DC+AD)
=(AB+BC+AD)﹣(AC+BC+AD)
=AB﹣AC
=10﹣7
=3,
故△ABD的周长比△ACD的周长大3.
23.如图,在△ABC中,∠B=40°,∠BCD=100°,CE平分∠ACB.
求∠A和∠BEC的度数.
【考点】三角形内角和定理;三角形的外角性质.
【答案】见试题解答内容
【分析】由∠B=40°,∠BCD=100°,根据三角形外角的性质可得到∠A=∠BCD﹣∠B=100°﹣40°=60°;再根据邻补角的定义得到∠ACB=180°﹣100°=80°,利用角平分线的定义得到∠BCE=40°,最后根据三角形的内角和定理求出∠BEC的度数.
【解答】解:∵∠B=40°,∠BCD=100°,
∴∠A=∠BCD﹣∠B=100°﹣40°=60°,
又∵∠BCD=100°,
∴∠ACB=180°﹣100°=80°,
而CE平分∠ACB,
∴∠BCE=40°,
∴∠BEC=180°﹣∠B﹣∠BCE=180°﹣40°﹣40°=100°.
故答案为:∠A和∠BEC的度数分别为60°,100°.
24.如图,在凹四边形ABCD中,∠A=45°,∠B=55°,∠D=20°,求∠BCD的度数.
下面是学习小组的同学们交流时得到的解决问题的三种方法:
方法一:作射线AC;
方法二:延长BC交AD于点E;
方法三:连接BD.
请选择上述一种方法,求∠BCD的度数.
【考点】多边形内角与外角.
【答案】∠BCD的度数是120°.
【分析】通过延长BC交AD于点E,运用三角形的外角等于和它不相邻两内角的和进行求解.
【解答】解:延长BC交AD于点E,
∴∠CED=∠A+∠B,∠BCD=∠CED+∠D,
∴∠BCD=∠A+∠B+∠D
=45°+55°+20°
=120°,
即∠BCD的度数是120°.
25.如图所示,在四边形ABCD中,AB∥DC,点P为BC上一点,设∠CDP=α,∠DPC=β,当点P在边BC上(不包括点C)运动时,α,β与∠B有什么关系?
【考点】多边形内角与外角;平行线的性质.
【答案】见试题解答内容
【分析】在△CDP中,先由三角形内角和为180°,得出α+β=180°﹣∠C;再由AB∥CD,根据平行线的性质,得出∠B=180°﹣∠C;从而得出α+β=∠B.
【解答】解:在△CDP中,∵∠CDP+∠CPD+∠C=180°,∠CDP=α,∠CPD=β,
∴α+β=∠CDP+∠CPD=180°﹣∠C;
∵AB∥CD,
∴∠B+∠C=180°,
∴∠B=180°﹣∠C;
∴α+β=∠B.
