苏教版数学必修5 第12章 数列
图片预览






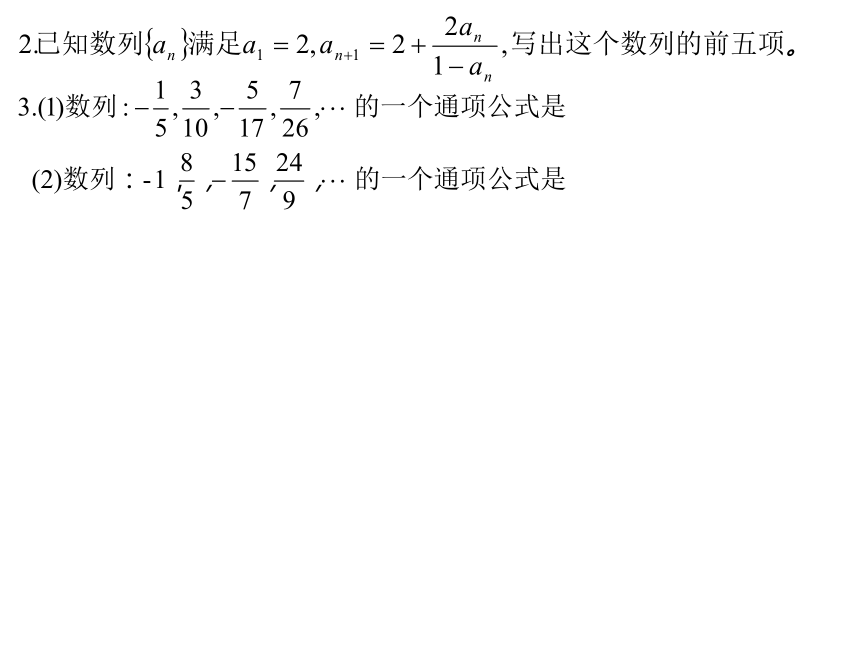





文档简介
课件41张PPT。 第12章 数 列 第一课时 12。1 数列教学目标:1、理解数列的概念;
2、明确数列的通用公式是数列的项与对应序号的关系式,能根据数列的
部分项能归纳出数列的通项公式;
3、能用数列的通项公式求出数列的任一项。教学重点:数列的概念及数列的通项公式。
教学过程:一、问题情景:
国际象棋的传说故事,……,各个格子里的麦粒数依次是1,2,22,23,24…,263.
麦粒总数是:1+2+22+23+…+263须用公式求出其和,这将是我们今后将要解决的问题。二、实例:
例1:堆放钢管共7层,自上而下各层的钢管数排成一列数: 4,5,6,7,8,9,10。①
例2 :正整数的倒数排成一列数: ②的精确到1,0.1,0.01,0.001,… 的不足近似值排成一列数:
1,1.4,1.41,1.414,… ③-1,1,-1,1,-1,1,… ④1,1,1,… ⑤三、构建数学:概念:
1、数列:按一定次序排列的一列数叫做数列。
项:数列中的每一个数都叫做这个数列的项;
2、数列的一般形式: 3、数列的通项公式:
定义:如果数列{an}的第n项an与n之间的关系可以用一个公式来表示,那么这个
公式就叫做这个数列的通项公式。数列的通项公式也就是相应函数的解析式。数列①的通项公式:an=n+3 (n≤7)数列②的通项公式:an=1/n4、数列的图象表示:
它们都是一群孤立的点。5、数列的分类:
1、有穷数列------- 项数有限的数列。如数列①
2、无穷数列--------项数无穷的数列。如数列②③④⑤四、例题讲解:
例1 根据下面数列{ an}的通项公式,写出它的前5项:例2 写出下面数列的一个通项公式,使它的前4项分别是下列各数:例3 已知数列{an}的通项公式为an=2n2-n,问45是此数列中的项吗?3呢?为什么?集中练习:P112 练习:1~4五、作业题:
P114 习题 3.1 1(双数小题);
2;第二课时 数列(2)教学目标:理解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项;
结合函数的单调性,理解递境数列、递减数列、常数列。教学重点:数列的递推公式。
教学过程:一、数列的递推公式:
数列 4,5,6,7,8,9,10。①通项公式: an=n+3(n≤7)另:a1=4, a2=5=a1+1 ,a3=6=a2+1,…, a7=10=a6+1,
即有:a1=4, an=an-1+1(2≤n≤7)1、定义:如果已知数列{an}的第1项(或前n项),且任一项an与它的前一项an-1(或前n项)间的关系可以用一个公式来表示,那么这个公式叫做这个数列的递推公式。二、构建数学:2、例题:
例1 已知数列{an}的第1项是1,以后的各项由公式
给出,写出这个数列的前5项。例2 在数列{an}中,已a1=2,a2=3,an+2=3an+1-2an(n≥1),写出此数列的前6项。3、集练:P113练习: 1~3三、递增数列、递减数列、常数列
1、定义:若an+1>an对任意的正整数n都成立,则数列{an}称为递增数列。若an+1 2、掌握等差数列的通项公式,并能运用通项公式解决一些简单问题。
教学重点:等差数列的概念、通项公式。
教学过程:一、问题情景:
数列①: 4,5,6,7,8,9,10;
数列②:3,0,-3,-6,…
数列③:
数列④ :1,3,5,7,…。二、学生活动:
1、这些数列有什么共同特点?特点:从第二项起,每一项与它的前一项的差都等于1。特点:从第二项起,每一项与它的前一项的差都等于-3。特点:从第二项起,每一项与它的前一项的差都等于1/10。特点:从第二项起,每一项与它的前一项的差都等于2。从第二项起,每一项与它的前一项的差都等于同一个常数。2、说出上述数列①~④各有什么特点:三、构建数学:
1、 等差数列的定义:
等差数列的公差:用d表示,写出数列①~④的d.2、等差数列的通项公式:
等差数列{an}的首项为a1,公差为d,则
an=a1+(n-1)d理解:(1)当n=1时,左边=a1,右边=a1,即等式成立。即当n∈N*时公式也成立。
(2)求出数列②③④的通项公式;
(3)通项公式中的四个基本量a1,an,n,d,用方程的观点知三求一。四、例题:
P115 例1 解析:(1)利用公式求出指定项。为此先要找出首项a1,公差d及项数n,
然后代入公式,就可求出相应的项。(2)判断一个数是否是一个数列的项,这个问题是第(1)的相反的问题。P116 例2 解析:此题是已知等差数列的两项,求首项a1及公差d.通过布列方程组求解。P116 例3 解析:实际问题相当于已知等差数列的首项、末项及项数,求公差。补例1: 数列{an}各项的倒数组成一个等差数列,若2、一个无穷等差数列的首项是由3,公差是-7;另一个无穷等差数列的首项是17,公差
是12,这两个数列中存在着序号及数值相等的项吗?等差数列(二)教学目标:掌握等差中项的概念及应用;
能利用等差数列的基础知识,导出等差数列的一些性质并会应用。教学重点:等差中项及等差数列的性质。
教学过程:一、问题情景:
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A满足什么条件?
二、学生讨论:三、构建数学:
1、定义:如果a,A,b成等差数列,那么A叫做a与b的等差中项。2、结论(1)两个数的等差中项就是这两个数的算术平均数;
(2)在一个公差是d的无穷等差数列{an}中,an是它的前一项与后一项的
等差中项(n≥2).(3)如果已知三个数成等差数列,可设这三个数为a-d,a,a+d(d为公差),使解题简便。如果已知四个数成等差数列,可设这四个数为a-3d,a-d,a+d,a+3d(公差为d).四、例题讲解:
1、 P117例4 解析:此题是已知数列的通项公式,判断它是否等差数列。关键是考查相邻两项
的差是否为一个常数。结论:如果an关于n的一次式,那么{an}是等差数列。等差数列的图象是一直线
上的均匀排开的无穷多个孤立点。2、已知五个数成等差数列,它们的和等于5,平方和为85/9,求这五个数。解析:设第3个数为a3,公差为d,则这五个数分别是这种“对称性”的设法对解题创立了十分便利的条件。利用巧设达到简解之目的。 一、等差数列的有关性质:若{an}是等差数列,公差为d,则:三、例题:二、数列{an}的通项an与前n项和Sn之间的关系:三、集练:
1、一个等差数列中a15=33,a25=66,则a35= .2、48, a, b, c, -12是等差数列中的连续五项,则a,b,c的值依次为 。 3、在等差数列{an}中,若a3+a4+a5+a6+a7=450,则a2+a8的值等于 ( )
A.45 B.75 C.180 D.3004、已知等差数列的前n项和为7n2-5n,则a100= .6.已知数列{an},若an=-2n+25,则Sn达到最大值时的n为 A.13 B.12 C.11 D.107.等差数列的首项是2,第二项与第三项分别是两个连续正整数的平方,求此数列。8.已知数列{an}的前n项和为Sn=3n2-2n,求证:数列{an}是等差数列。等 差 数 列 前 n 项 和教学目标:1、掌握等差数列的前n项和公式及推导公式的思想、方法;
2、会运用公式解决一些简单问题,并能将等差数列的通项公式与前n项和
公式结合起来运用。教学重点:等差数列的前n项和公式及运用。
教学过程: 一、问题情景:
1+2+3+4+5+…+99+100=?
著名数学家高斯10岁时曾很快求出它的结果。你知道如何计算的?二、学生活动:1、此问题是求等差数列 1,2,3,…,n,… 的前100项的和。2、3、如何求等差数列:a1,a2,a3,…,an,… 前n项和?三、数学构建:
1、等差数列前n项和Sn公式推导:
设等差数列[an}的公差为d,前n项和为Sn,
则由倒序相加法,得2Sn=n(a1+an) 语言叙述:等差数列的前n项和等于首末两项的和与项数乘积的一半。2、等差数列前n项和公式:四、数学应用:
1、例题; 例1 等差数列{an}中,S10=120,那么a1+a10的值是 ( )
A.12 B.24 C.36 D.48例2 等差数列{an}和{bn}中,a1=25,b1=75,a100+b100=100,则数列{an+bn}的前期100项
之和为 ( )
A.0 B.100 C. 1000 D.10000 例3 (P120例1) 一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它
下面一层多放一支,最上面一层放120支。这个V形架上共放着多少支铅笔?解析:应用题问题,将实际问题转化为数学问题——等差数列。
解详见教材P120(略)。例4 等差数列-10,-6,-2,2,…前多少项的和是54?解析:首先创立解题情景。设等差数列为{an},前n项和是Sn.再由第二个公式列出关于n的方程,求这个方程的正整数解即可。解(见P120-121,略)解析:先通过求一个一次不等式的正整数解,确定集合的元素的个数,再把这些
元素列出,组成一个等差数列,最后求和。例6 在等差数列{an}中,a4=0.8,a11=2.2,求a51+a52+…+a80 .解析:应用等差数列的通项公式及前n项和公式解题。2、集中练习:
P122 练习: 1~6五、小结:熟练应用等差数列的二个求和公式及通项公式。六、作业:
P122-123 习题 3.3 1(1)(2)(4);
2(2)(4);
5; 7.等差数列的前n项和(二)教学目标:灵活运用等差数列的前n项和公式及性质解一些简单问题。教学过程:
一、等差数列的前n项和公式:二、等差数列的性质:
1、数列{an}成等差数列的等价条件是证明:P117 例4 等差数列的通项公式an是关于n的一次函数。2、、数列{an}成等差数列的等价条件是特例:P121-122 例4
结论:等差数列前n项和Sn是关于n的二次函数(无常数项)特例:讲解 P123 习题10. 由特殊到一般即得。三、数学应用:
1、例1 已知数列{an}为等差数列,Sn=25,S2n=100,则S3n为 ( )。
A.125 B.175 C.225 D.250 例2 、一个等差数列的前10项之和为100,前100项之和为10,求前110项之和。解法1:性质求解;
解法2:取特殊值法;
解法3:通解通法——公式法求解。 解析:本题解法较多,技巧性较强。探求研究,寻求简捷的解题方法。解法1:通性通法(先求首项和公差)
解法2:待定系数法
解法3:性质求解(1)数列{-2n2+29n+3}中的最大项是 ( )
A.107 B.108 C. D.1092、集中练习: (2)等差数列100,96,92,……的第 项开始,以后各项均为负值。(3)设等差数列{an}中,
①已知a1=1,求公差d,使a1a3+a2a3最小;
②已知a7=9,求d,使a1a3最小。(5)首项为3,公差为2的等差数列,Sk为其前k项之和,则8.已知等差数列{an} 中,前30项的和S30=50,前50项的和S50=30,求前80项的和。7 .在等差数列{an}中,a1=13,S3=S11,则Sn的最大值为 .知识补充:设数列{an}为等差数列,其奇数项之和为S奇,偶数项之和为S偶,那么
当项数为偶数2n 时,S偶-S奇=nd,
当项数为奇数2n-1时,集练:《优》P78强化训练 1,2,8。等 比 数 列 (1)教学目标:1、理解等比数列的概念,掌握等比中项的概念;
2、掌握等比数列的通项公式,并能运用通项公式解决一些简单问题。教学重点:概念及通项公式。
教学过程:一、问题情景:
1、国际象棋棋盘各格子里放麦粒问题,得到数列:1,2,4,8 ,…,263; ①又 5,25,125,625,… ②③-1,1,-1,1,… ④1,1,1,1,… ⑤2、学生活动:
共同特点:每个数列从第二项起,每一项与它的前一项的比都等于同一个常数。二、构建数学:
1、等比数列的定义:
这个常数叫做等比数列的公比,公比通常用q表示(q≠0)分别求出①,②,③,④,⑤的公比q 。理解:等比数列的任意一项都不为0,公比q也不为0;
如果an/an-1都是同一个常数,那么{an}就是等比数列。2、等比数列的通项公式:数列①的通项公式:3、等比数列的图象表示:数列①的图象 P127图3-5三、数学应用:
1、例题讲解:
例1 ~例3 ( 见P127-128 略)2、等比数列的性质:
已知{an},{bn}是等比数列,则{anbn}是等比数列。
特例:{an}是等比数列,c≠0,则{can}是等比数列。3、等比中项
(1) 定义:如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b
的等比中项。(2)理解:同号两数才有等比中项;
等比中项有两个,它们互为相反数。(3)等比数列从第2项起,每一项(有穷等比数列的末项除外)是它的前一项与后
一项的等比中项。(4)当a>0,b>0时, 叫做a,b的几何平均数。四、集练:P128 练习:1~5;五、作业题:P129 1(2)(3)
5,6,7,9。等比数列 (2)教学目标;能用等比数列的基础知识导出一些性质并会运用。教学过程:
一、等比数列的性质:二、等比数列解题的基本方法:
1、灵活运用等比数列的各种性质解题;三、数学应用:
1、一个等比数列的前三项依次是a,2a+2,3a+3,试问 是否为这个数列中的一项? 如果是,是它的第几项?2、已知数列{an}的前n项和为Sn=3n-1,求证{an}是等比数列。3、等比数列的前三项和为168, a2-a5=42,求a5,a7的等比中项。4、已知三个数成等比数列,它们的积为27,它们的平方和为91,求这三个数。等比数列的前n项和(1)教学目标:1、掌握等比数列的前n项和公式及推导公式的思路、方法;
2、会运用公式解决一些实际问题;
3、能将等比数列的的通项公式与前n项和公式结合起来运用。
教学重点;等比数列的前n项和公式及其应用。
教学过程:一、问题情景:
如何求: 1,2,22,23,…,262,263 的和
S64=1+2+22+23+…+262+263 ①二、学生活动:
1、用公比2乘①式,
错位相消法, S64=264 – 1
讲解P130的注释。2、设等比数列{an}:a1,a2,a3,…,an…的公比为q,如何求前n项的和?
从前面的求和方法得到那些启示。三、构建数学:
1、等比数列的前n项和的公式:当q=1时,Sn=na1.2、等比数列中的五个基本量a1,q,ann,Sn,可知三求二,列方程组是求解的常用方法。四、数学应用:
1、引例中提出的问题:
2、例题讲解:P131-134 例1~例3五、集练: P132 练习:1~3;
六、作业:P133 习题3.5 1~5.等比数列的前n项和(2)教学目标:1、灵活运用等比数列前n 项和公式,理解等比数列前n项和的性质并应用;
2、了解一些特殊数列的求和方法。
教学重点:等比数列前n项和性质,求和方法。
教学过程:一、等比数列前n项和的性质:
已知数列{ an}是等比数列,Sn是其n项和,Sn,S2n-Sn,S3n-S2n 成等比数列。
P133 练习 :4;二、例题讲解:
1、已知等比数列{an}中,a1+a2=30, a3+a4=120,则a5+a6= . . .等差数列、等比数列习题课教学目标:特殊数列的求和(能用拆项法、裂项法将所给数列分拆为等差、等比
数列求和;或用“错位相减法”“倒序相加法”等方法),体现化归思想。教学过程;
一、常用的前n项和公式:二、一般数列求和及常用的方法: 数 列 总 复 习高考重点要求:
1、知识点:数列、等差数列及其通项公式、等差数列前n项和公式、等比数列及其
通项公式、等比数列前n项和公式 。
2、重点是数列通项公式的求法、数列前n项和公式;难点是等差数列等比数列的应用。 典型考题:
1、已知数列{an}的第1项是1,以后的各项由
给出。 (1)写出数列{an}的前5项;
(2)求通项公式。3、等差数列{an}的前n项和为Sn,若a3+a17=10,则S19值是 ( )
A.55 B.95 C.100 D.不能确定4、若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和为390,
则这个数列有 ( )
A. 13项 B.12项 C.11项 D.10项5、设等差数列{an}共有3n项,它的前2n项之和是100, 后2n项之和是200,
则该等差数列的中间n项之和等于 。
9、已知Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列,
求证:a2,a8,a5 成等差数列。
2、明确数列的通用公式是数列的项与对应序号的关系式,能根据数列的
部分项能归纳出数列的通项公式;
3、能用数列的通项公式求出数列的任一项。教学重点:数列的概念及数列的通项公式。
教学过程:一、问题情景:
国际象棋的传说故事,……,各个格子里的麦粒数依次是1,2,22,23,24…,263.
麦粒总数是:1+2+22+23+…+263须用公式求出其和,这将是我们今后将要解决的问题。二、实例:
例1:堆放钢管共7层,自上而下各层的钢管数排成一列数: 4,5,6,7,8,9,10。①
例2 :正整数的倒数排成一列数: ②的精确到1,0.1,0.01,0.001,… 的不足近似值排成一列数:
1,1.4,1.41,1.414,… ③-1,1,-1,1,-1,1,… ④1,1,1,… ⑤三、构建数学:概念:
1、数列:按一定次序排列的一列数叫做数列。
项:数列中的每一个数都叫做这个数列的项;
2、数列的一般形式: 3、数列的通项公式:
定义:如果数列{an}的第n项an与n之间的关系可以用一个公式来表示,那么这个
公式就叫做这个数列的通项公式。数列的通项公式也就是相应函数的解析式。数列①的通项公式:an=n+3 (n≤7)数列②的通项公式:an=1/n4、数列的图象表示:
它们都是一群孤立的点。5、数列的分类:
1、有穷数列------- 项数有限的数列。如数列①
2、无穷数列--------项数无穷的数列。如数列②③④⑤四、例题讲解:
例1 根据下面数列{ an}的通项公式,写出它的前5项:例2 写出下面数列的一个通项公式,使它的前4项分别是下列各数:例3 已知数列{an}的通项公式为an=2n2-n,问45是此数列中的项吗?3呢?为什么?集中练习:P112 练习:1~4五、作业题:
P114 习题 3.1 1(双数小题);
2;第二课时 数列(2)教学目标:理解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项;
结合函数的单调性,理解递境数列、递减数列、常数列。教学重点:数列的递推公式。
教学过程:一、数列的递推公式:
数列 4,5,6,7,8,9,10。①通项公式: an=n+3(n≤7)另:a1=4, a2=5=a1+1 ,a3=6=a2+1,…, a7=10=a6+1,
即有:a1=4, an=an-1+1(2≤n≤7)1、定义:如果已知数列{an}的第1项(或前n项),且任一项an与它的前一项an-1(或前n项)间的关系可以用一个公式来表示,那么这个公式叫做这个数列的递推公式。二、构建数学:2、例题:
例1 已知数列{an}的第1项是1,以后的各项由公式
给出,写出这个数列的前5项。例2 在数列{an}中,已a1=2,a2=3,an+2=3an+1-2an(n≥1),写出此数列的前6项。3、集练:P113练习: 1~3三、递增数列、递减数列、常数列
1、定义:若an+1>an对任意的正整数n都成立,则数列{an}称为递增数列。若an+1
教学重点:等差数列的概念、通项公式。
教学过程:一、问题情景:
数列①: 4,5,6,7,8,9,10;
数列②:3,0,-3,-6,…
数列③:
数列④ :1,3,5,7,…。二、学生活动:
1、这些数列有什么共同特点?特点:从第二项起,每一项与它的前一项的差都等于1。特点:从第二项起,每一项与它的前一项的差都等于-3。特点:从第二项起,每一项与它的前一项的差都等于1/10。特点:从第二项起,每一项与它的前一项的差都等于2。从第二项起,每一项与它的前一项的差都等于同一个常数。2、说出上述数列①~④各有什么特点:三、构建数学:
1、 等差数列的定义:
等差数列的公差:用d表示,写出数列①~④的d.2、等差数列的通项公式:
等差数列{an}的首项为a1,公差为d,则
an=a1+(n-1)d理解:(1)当n=1时,左边=a1,右边=a1,即等式成立。即当n∈N*时公式也成立。
(2)求出数列②③④的通项公式;
(3)通项公式中的四个基本量a1,an,n,d,用方程的观点知三求一。四、例题:
P115 例1 解析:(1)利用公式求出指定项。为此先要找出首项a1,公差d及项数n,
然后代入公式,就可求出相应的项。(2)判断一个数是否是一个数列的项,这个问题是第(1)的相反的问题。P116 例2 解析:此题是已知等差数列的两项,求首项a1及公差d.通过布列方程组求解。P116 例3 解析:实际问题相当于已知等差数列的首项、末项及项数,求公差。补例1: 数列{an}各项的倒数组成一个等差数列,若2、一个无穷等差数列的首项是由3,公差是-7;另一个无穷等差数列的首项是17,公差
是12,这两个数列中存在着序号及数值相等的项吗?等差数列(二)教学目标:掌握等差中项的概念及应用;
能利用等差数列的基础知识,导出等差数列的一些性质并会应用。教学重点:等差中项及等差数列的性质。
教学过程:一、问题情景:
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A满足什么条件?
二、学生讨论:三、构建数学:
1、定义:如果a,A,b成等差数列,那么A叫做a与b的等差中项。2、结论(1)两个数的等差中项就是这两个数的算术平均数;
(2)在一个公差是d的无穷等差数列{an}中,an是它的前一项与后一项的
等差中项(n≥2).(3)如果已知三个数成等差数列,可设这三个数为a-d,a,a+d(d为公差),使解题简便。如果已知四个数成等差数列,可设这四个数为a-3d,a-d,a+d,a+3d(公差为d).四、例题讲解:
1、 P117例4 解析:此题是已知数列的通项公式,判断它是否等差数列。关键是考查相邻两项
的差是否为一个常数。结论:如果an关于n的一次式,那么{an}是等差数列。等差数列的图象是一直线
上的均匀排开的无穷多个孤立点。2、已知五个数成等差数列,它们的和等于5,平方和为85/9,求这五个数。解析:设第3个数为a3,公差为d,则这五个数分别是这种“对称性”的设法对解题创立了十分便利的条件。利用巧设达到简解之目的。 一、等差数列的有关性质:若{an}是等差数列,公差为d,则:三、例题:二、数列{an}的通项an与前n项和Sn之间的关系:三、集练:
1、一个等差数列中a15=33,a25=66,则a35= .2、48, a, b, c, -12是等差数列中的连续五项,则a,b,c的值依次为 。 3、在等差数列{an}中,若a3+a4+a5+a6+a7=450,则a2+a8的值等于 ( )
A.45 B.75 C.180 D.3004、已知等差数列的前n项和为7n2-5n,则a100= .6.已知数列{an},若an=-2n+25,则Sn达到最大值时的n为 A.13 B.12 C.11 D.107.等差数列的首项是2,第二项与第三项分别是两个连续正整数的平方,求此数列。8.已知数列{an}的前n项和为Sn=3n2-2n,求证:数列{an}是等差数列。等 差 数 列 前 n 项 和教学目标:1、掌握等差数列的前n项和公式及推导公式的思想、方法;
2、会运用公式解决一些简单问题,并能将等差数列的通项公式与前n项和
公式结合起来运用。教学重点:等差数列的前n项和公式及运用。
教学过程: 一、问题情景:
1+2+3+4+5+…+99+100=?
著名数学家高斯10岁时曾很快求出它的结果。你知道如何计算的?二、学生活动:1、此问题是求等差数列 1,2,3,…,n,… 的前100项的和。2、3、如何求等差数列:a1,a2,a3,…,an,… 前n项和?三、数学构建:
1、等差数列前n项和Sn公式推导:
设等差数列[an}的公差为d,前n项和为Sn,
则由倒序相加法,得2Sn=n(a1+an) 语言叙述:等差数列的前n项和等于首末两项的和与项数乘积的一半。2、等差数列前n项和公式:四、数学应用:
1、例题; 例1 等差数列{an}中,S10=120,那么a1+a10的值是 ( )
A.12 B.24 C.36 D.48例2 等差数列{an}和{bn}中,a1=25,b1=75,a100+b100=100,则数列{an+bn}的前期100项
之和为 ( )
A.0 B.100 C. 1000 D.10000 例3 (P120例1) 一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它
下面一层多放一支,最上面一层放120支。这个V形架上共放着多少支铅笔?解析:应用题问题,将实际问题转化为数学问题——等差数列。
解详见教材P120(略)。例4 等差数列-10,-6,-2,2,…前多少项的和是54?解析:首先创立解题情景。设等差数列为{an},前n项和是Sn.再由第二个公式列出关于n的方程,求这个方程的正整数解即可。解(见P120-121,略)解析:先通过求一个一次不等式的正整数解,确定集合的元素的个数,再把这些
元素列出,组成一个等差数列,最后求和。例6 在等差数列{an}中,a4=0.8,a11=2.2,求a51+a52+…+a80 .解析:应用等差数列的通项公式及前n项和公式解题。2、集中练习:
P122 练习: 1~6五、小结:熟练应用等差数列的二个求和公式及通项公式。六、作业:
P122-123 习题 3.3 1(1)(2)(4);
2(2)(4);
5; 7.等差数列的前n项和(二)教学目标:灵活运用等差数列的前n项和公式及性质解一些简单问题。教学过程:
一、等差数列的前n项和公式:二、等差数列的性质:
1、数列{an}成等差数列的等价条件是证明:P117 例4 等差数列的通项公式an是关于n的一次函数。2、、数列{an}成等差数列的等价条件是特例:P121-122 例4
结论:等差数列前n项和Sn是关于n的二次函数(无常数项)特例:讲解 P123 习题10. 由特殊到一般即得。三、数学应用:
1、例1 已知数列{an}为等差数列,Sn=25,S2n=100,则S3n为 ( )。
A.125 B.175 C.225 D.250 例2 、一个等差数列的前10项之和为100,前100项之和为10,求前110项之和。解法1:性质求解;
解法2:取特殊值法;
解法3:通解通法——公式法求解。 解析:本题解法较多,技巧性较强。探求研究,寻求简捷的解题方法。解法1:通性通法(先求首项和公差)
解法2:待定系数法
解法3:性质求解(1)数列{-2n2+29n+3}中的最大项是 ( )
A.107 B.108 C. D.1092、集中练习: (2)等差数列100,96,92,……的第 项开始,以后各项均为负值。(3)设等差数列{an}中,
①已知a1=1,求公差d,使a1a3+a2a3最小;
②已知a7=9,求d,使a1a3最小。(5)首项为3,公差为2的等差数列,Sk为其前k项之和,则8.已知等差数列{an} 中,前30项的和S30=50,前50项的和S50=30,求前80项的和。7 .在等差数列{an}中,a1=13,S3=S11,则Sn的最大值为 .知识补充:设数列{an}为等差数列,其奇数项之和为S奇,偶数项之和为S偶,那么
当项数为偶数2n 时,S偶-S奇=nd,
当项数为奇数2n-1时,集练:《优》P78强化训练 1,2,8。等 比 数 列 (1)教学目标:1、理解等比数列的概念,掌握等比中项的概念;
2、掌握等比数列的通项公式,并能运用通项公式解决一些简单问题。教学重点:概念及通项公式。
教学过程:一、问题情景:
1、国际象棋棋盘各格子里放麦粒问题,得到数列:1,2,4,8 ,…,263; ①又 5,25,125,625,… ②③-1,1,-1,1,… ④1,1,1,1,… ⑤2、学生活动:
共同特点:每个数列从第二项起,每一项与它的前一项的比都等于同一个常数。二、构建数学:
1、等比数列的定义:
这个常数叫做等比数列的公比,公比通常用q表示(q≠0)分别求出①,②,③,④,⑤的公比q 。理解:等比数列的任意一项都不为0,公比q也不为0;
如果an/an-1都是同一个常数,那么{an}就是等比数列。2、等比数列的通项公式:数列①的通项公式:3、等比数列的图象表示:数列①的图象 P127图3-5三、数学应用:
1、例题讲解:
例1 ~例3 ( 见P127-128 略)2、等比数列的性质:
已知{an},{bn}是等比数列,则{anbn}是等比数列。
特例:{an}是等比数列,c≠0,则{can}是等比数列。3、等比中项
(1) 定义:如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b
的等比中项。(2)理解:同号两数才有等比中项;
等比中项有两个,它们互为相反数。(3)等比数列从第2项起,每一项(有穷等比数列的末项除外)是它的前一项与后
一项的等比中项。(4)当a>0,b>0时, 叫做a,b的几何平均数。四、集练:P128 练习:1~5;五、作业题:P129 1(2)(3)
5,6,7,9。等比数列 (2)教学目标;能用等比数列的基础知识导出一些性质并会运用。教学过程:
一、等比数列的性质:二、等比数列解题的基本方法:
1、灵活运用等比数列的各种性质解题;三、数学应用:
1、一个等比数列的前三项依次是a,2a+2,3a+3,试问 是否为这个数列中的一项? 如果是,是它的第几项?2、已知数列{an}的前n项和为Sn=3n-1,求证{an}是等比数列。3、等比数列的前三项和为168, a2-a5=42,求a5,a7的等比中项。4、已知三个数成等比数列,它们的积为27,它们的平方和为91,求这三个数。等比数列的前n项和(1)教学目标:1、掌握等比数列的前n项和公式及推导公式的思路、方法;
2、会运用公式解决一些实际问题;
3、能将等比数列的的通项公式与前n项和公式结合起来运用。
教学重点;等比数列的前n项和公式及其应用。
教学过程:一、问题情景:
如何求: 1,2,22,23,…,262,263 的和
S64=1+2+22+23+…+262+263 ①二、学生活动:
1、用公比2乘①式,
错位相消法, S64=264 – 1
讲解P130的注释。2、设等比数列{an}:a1,a2,a3,…,an…的公比为q,如何求前n项的和?
从前面的求和方法得到那些启示。三、构建数学:
1、等比数列的前n项和的公式:当q=1时,Sn=na1.2、等比数列中的五个基本量a1,q,ann,Sn,可知三求二,列方程组是求解的常用方法。四、数学应用:
1、引例中提出的问题:
2、例题讲解:P131-134 例1~例3五、集练: P132 练习:1~3;
六、作业:P133 习题3.5 1~5.等比数列的前n项和(2)教学目标:1、灵活运用等比数列前n 项和公式,理解等比数列前n项和的性质并应用;
2、了解一些特殊数列的求和方法。
教学重点:等比数列前n项和性质,求和方法。
教学过程:一、等比数列前n项和的性质:
已知数列{ an}是等比数列,Sn是其n项和,Sn,S2n-Sn,S3n-S2n 成等比数列。
P133 练习 :4;二、例题讲解:
1、已知等比数列{an}中,a1+a2=30, a3+a4=120,则a5+a6= . . .等差数列、等比数列习题课教学目标:特殊数列的求和(能用拆项法、裂项法将所给数列分拆为等差、等比
数列求和;或用“错位相减法”“倒序相加法”等方法),体现化归思想。教学过程;
一、常用的前n项和公式:二、一般数列求和及常用的方法: 数 列 总 复 习高考重点要求:
1、知识点:数列、等差数列及其通项公式、等差数列前n项和公式、等比数列及其
通项公式、等比数列前n项和公式 。
2、重点是数列通项公式的求法、数列前n项和公式;难点是等差数列等比数列的应用。 典型考题:
1、已知数列{an}的第1项是1,以后的各项由
给出。 (1)写出数列{an}的前5项;
(2)求通项公式。3、等差数列{an}的前n项和为Sn,若a3+a17=10,则S19值是 ( )
A.55 B.95 C.100 D.不能确定4、若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和为390,
则这个数列有 ( )
A. 13项 B.12项 C.11项 D.10项5、设等差数列{an}共有3n项,它的前2n项之和是100, 后2n项之和是200,
则该等差数列的中间n项之和等于 。
9、已知Sn是等比数列{an}的前n项和,S3,S9,S6成等差数列,
求证:a2,a8,a5 成等差数列。
