3.1勾股定理提优练习2023-2024学年苏科版数学八年级上册(无答案)
文档属性
| 名称 | 3.1勾股定理提优练习2023-2024学年苏科版数学八年级上册(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 252.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-04 00:00:00 | ||
图片预览


文档简介
3.1勾股定理(提优练习)
选择题(本题共10小题)
1.在一个直角三角形中,若斜边的长是13,一条直角边的长为5,那么这个直角三角形的面积是( )
A.30 B.40 C.50 D.60
2.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
3.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
4.一直角三角形的三边分别为2,3,x,那么以x为边长的正方形的面积为( )
A.13 B.5 C.4 D.13或5
5.如图,∠AOC=∠BOC,点P在OC上,PD⊥OA与点D,PE⊥OB与点E,若OD=4,OP=5,则PE的长为( )
A.3 B. C.4 D.
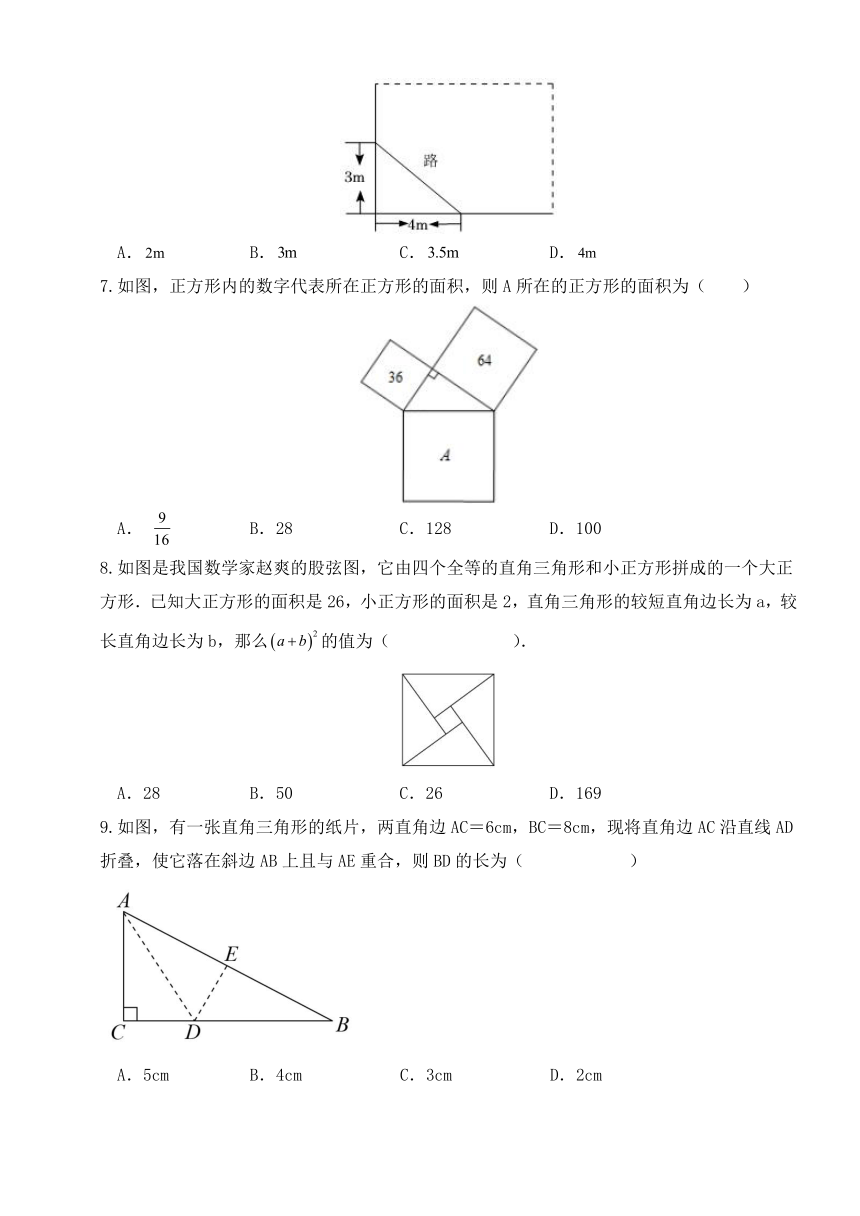
6.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了几步路,却踩伤了花草,他们少走的路长为( )
A. B. C. D.
7.如图,正方形内的数字代表所在正方形的面积,则A所在的正方形的面积为( )
A. B.28 C.128 D.100
8.如图是我国数学家赵爽的股弦图,它由四个全等的直角三角形和小正方形拼成的一个大正方形.已知大正方形的面积是26,小正方形的面积是2,直角三角形的较短直角边长为a,较长直角边长为b,那么的值为( ).
A.28 B.50 C.26 D.169
9.如图,有一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,则BD的长为( )
A.5cm B.4cm C.3cm D.2cm
10.在直线 l 上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别 为 a,b,c,正放置的四个正方形的面积依次为 S1,S2,S3,S4,则 S1+S2+S3+S4=( )
A.a+b B.b+c C.a+c D.a+b+c
填空题(本题共10小题)
11.已知直角三角形的两边长分别为3、4.则第三边长为________.
12.如果一个直角三角形的两条直角边的长分别为5、12,则斜边上的高的长度为______.
13.在直角三角形ABC中,斜边AB=1,则AB +BC +AC =______
14.在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=6cm,BC=8cm,则CD的长为 cm.
15.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长的直角边长为a,较短的直角边长为b,若ab=8,小正方形的面积为9,则大正方形的边长为 .
16.如图,以的两条直角边和斜边为边长分别作正方形,其中正方形、正方形的面积分别为25、144,则阴影部分的面积为______.
17.如图,在中,,,,将折叠,使点与点重合,得折痕,则的周长等于____cm.
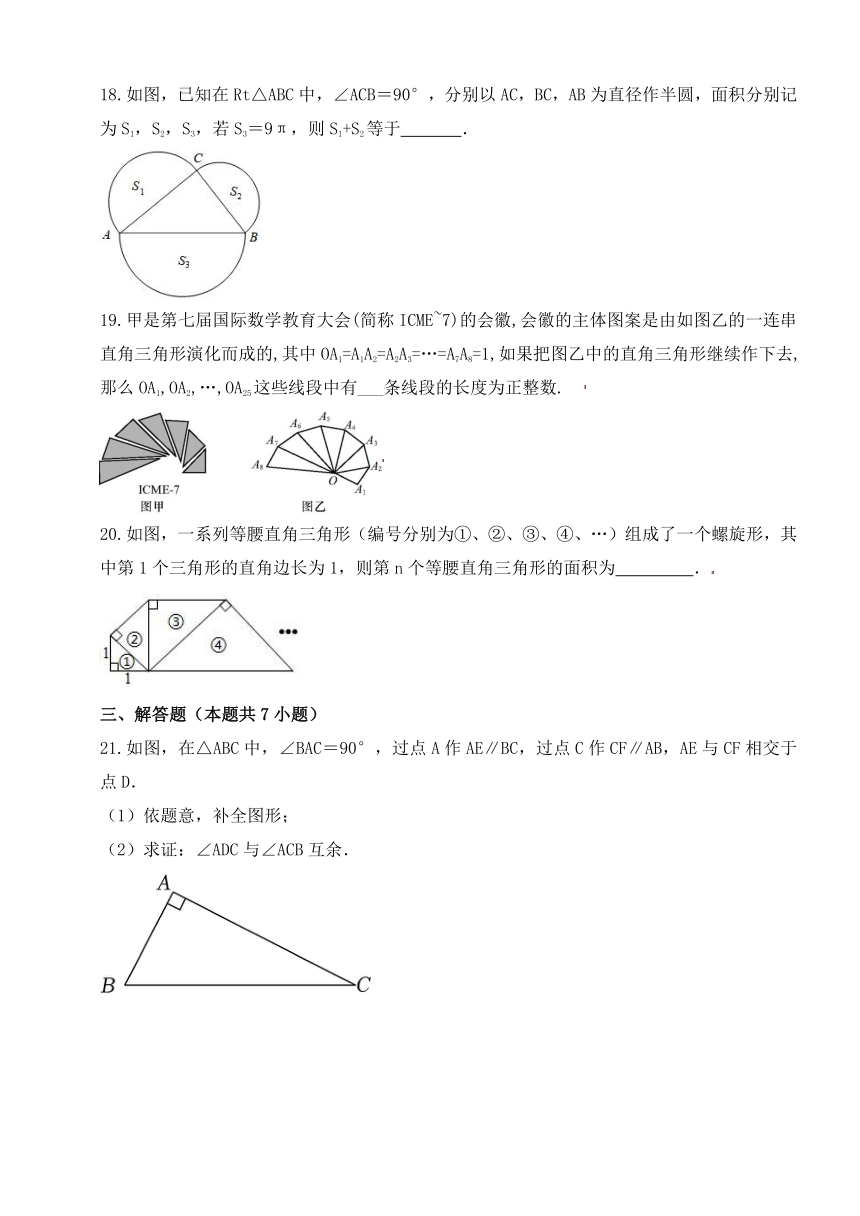
18.如图,已知在Rt△ABC中,∠ACB=90°,分别以AC,BC,AB为直径作半圆,面积分别记为S1,S2,S3,若S3=9π,则S1+S2等于 .
19.甲是第七届国际数学教育大会(简称ICME~7)的会徽,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,如果把图乙中的直角三角形继续作下去,那么OA1,OA2,…,OA25这些线段中有___条线段的长度为正整数.
20.如图,一系列等腰直角三角形(编号分别为①、②、③、④、…)组成了一个螺旋形,其中第1个三角形的直角边长为1,则第n个等腰直角三角形的面积为 .
解答题(本题共7小题)
21.如图,在△ABC中,∠BAC=90°,过点A作AE∥BC,过点C作CF∥AB,AE与CF相交于点D.
(1)依题意,补全图形;
(2)求证:∠ADC与∠ACB互余.
22.如图,在△ABC中,,于点D,,,.请求出△ABC的面积和CD的长.
23.公元3世纪,我国数学家赵爽在注《周髀算经》中,就利用下列弦图证明了勾股定理.即用4个全等的直角三角形拼成如图所示的正方形ABCD,中间留出一个小正方形空格.请你利用这个弦图证明勾股定理.
24.勾股定理被誉为“几何明珠”,在数学的发展历程中占有举足轻重的地位.它是初中数学中的重要知识点之一,也是初中学生以后解决数学问题和实际问题中常常运用到的重要知识,因此学好勾股定理非常重要.学习数学“不仅要知其然,更要知其所以然”,所以,我们要学会勾股定理的各种证明方法.请你利用如图图形证明勾股定理:
已知:如图,四边形ABCD中,BD⊥CD,AE⊥BD于点E,且△ABE≌△BCD.求证:AB2=BE2+AE2.
25.已知对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.
(1)若AB=5,OA=3,OC=4则BC=______;
(2)若,,则______;
(3)若AB=m,BC=n,CD=c,AD=d,则m,n,c,d之间的数量关系是______.
26.如图所示,在△ABC中,∠ACB=90°,AB=10,BC=6,点P从点A出发,以每秒2个单位长度的速度沿折线A﹣B﹣C方向,朝着点C运动.设点P的运动时间为t秒(t>0).
(1)在运动过程中,当t 取何值时,点P恰好在∠BAC的角平分线上;
(2)在运动过程中,当t 取何值时,△PBC是等腰三角形.
27.勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3的有 个;
②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为S1,S2,直角三角形面积为S3,请判断S1,S2,S3的关系并证明;
(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的“勾股树”.在如图9所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知∠1=∠2=∠3=∠α,则当∠α变化时,回答下列问题:(结果可用含m的式子表示)
①a2+b2+c2+d2= ;
②b与c的关系为 ,a与d的关系为 .
选择题(本题共10小题)
1.在一个直角三角形中,若斜边的长是13,一条直角边的长为5,那么这个直角三角形的面积是( )
A.30 B.40 C.50 D.60
2.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
3.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
4.一直角三角形的三边分别为2,3,x,那么以x为边长的正方形的面积为( )
A.13 B.5 C.4 D.13或5
5.如图,∠AOC=∠BOC,点P在OC上,PD⊥OA与点D,PE⊥OB与点E,若OD=4,OP=5,则PE的长为( )
A.3 B. C.4 D.
6.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了几步路,却踩伤了花草,他们少走的路长为( )
A. B. C. D.
7.如图,正方形内的数字代表所在正方形的面积,则A所在的正方形的面积为( )
A. B.28 C.128 D.100
8.如图是我国数学家赵爽的股弦图,它由四个全等的直角三角形和小正方形拼成的一个大正方形.已知大正方形的面积是26,小正方形的面积是2,直角三角形的较短直角边长为a,较长直角边长为b,那么的值为( ).
A.28 B.50 C.26 D.169
9.如图,有一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,则BD的长为( )
A.5cm B.4cm C.3cm D.2cm
10.在直线 l 上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别 为 a,b,c,正放置的四个正方形的面积依次为 S1,S2,S3,S4,则 S1+S2+S3+S4=( )
A.a+b B.b+c C.a+c D.a+b+c
填空题(本题共10小题)
11.已知直角三角形的两边长分别为3、4.则第三边长为________.
12.如果一个直角三角形的两条直角边的长分别为5、12,则斜边上的高的长度为______.
13.在直角三角形ABC中,斜边AB=1,则AB +BC +AC =______
14.在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=6cm,BC=8cm,则CD的长为 cm.
15.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长的直角边长为a,较短的直角边长为b,若ab=8,小正方形的面积为9,则大正方形的边长为 .
16.如图,以的两条直角边和斜边为边长分别作正方形,其中正方形、正方形的面积分别为25、144,则阴影部分的面积为______.
17.如图,在中,,,,将折叠,使点与点重合,得折痕,则的周长等于____cm.
18.如图,已知在Rt△ABC中,∠ACB=90°,分别以AC,BC,AB为直径作半圆,面积分别记为S1,S2,S3,若S3=9π,则S1+S2等于 .
19.甲是第七届国际数学教育大会(简称ICME~7)的会徽,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,如果把图乙中的直角三角形继续作下去,那么OA1,OA2,…,OA25这些线段中有___条线段的长度为正整数.
20.如图,一系列等腰直角三角形(编号分别为①、②、③、④、…)组成了一个螺旋形,其中第1个三角形的直角边长为1,则第n个等腰直角三角形的面积为 .
解答题(本题共7小题)
21.如图,在△ABC中,∠BAC=90°,过点A作AE∥BC,过点C作CF∥AB,AE与CF相交于点D.
(1)依题意,补全图形;
(2)求证:∠ADC与∠ACB互余.
22.如图,在△ABC中,,于点D,,,.请求出△ABC的面积和CD的长.
23.公元3世纪,我国数学家赵爽在注《周髀算经》中,就利用下列弦图证明了勾股定理.即用4个全等的直角三角形拼成如图所示的正方形ABCD,中间留出一个小正方形空格.请你利用这个弦图证明勾股定理.
24.勾股定理被誉为“几何明珠”,在数学的发展历程中占有举足轻重的地位.它是初中数学中的重要知识点之一,也是初中学生以后解决数学问题和实际问题中常常运用到的重要知识,因此学好勾股定理非常重要.学习数学“不仅要知其然,更要知其所以然”,所以,我们要学会勾股定理的各种证明方法.请你利用如图图形证明勾股定理:
已知:如图,四边形ABCD中,BD⊥CD,AE⊥BD于点E,且△ABE≌△BCD.求证:AB2=BE2+AE2.
25.已知对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.
(1)若AB=5,OA=3,OC=4则BC=______;
(2)若,,则______;
(3)若AB=m,BC=n,CD=c,AD=d,则m,n,c,d之间的数量关系是______.
26.如图所示,在△ABC中,∠ACB=90°,AB=10,BC=6,点P从点A出发,以每秒2个单位长度的速度沿折线A﹣B﹣C方向,朝着点C运动.设点P的运动时间为t秒(t>0).
(1)在运动过程中,当t 取何值时,点P恰好在∠BAC的角平分线上;
(2)在运动过程中,当t 取何值时,△PBC是等腰三角形.
27.勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3的有 个;
②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为S1,S2,直角三角形面积为S3,请判断S1,S2,S3的关系并证明;
(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的“勾股树”.在如图9所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知∠1=∠2=∠3=∠α,则当∠α变化时,回答下列问题:(结果可用含m的式子表示)
①a2+b2+c2+d2= ;
②b与c的关系为 ,a与d的关系为 .
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
