5.1.2垂线(1)(浙江省台州市)
文档属性
| 名称 | 5.1.2垂线(1)(浙江省台州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-02-25 00:00:00 | ||
图片预览



文档简介
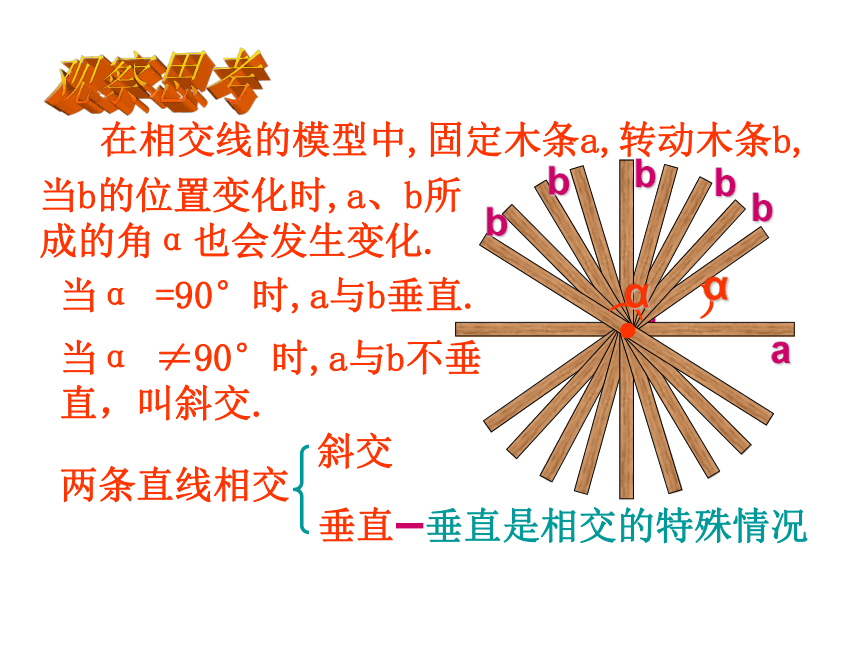
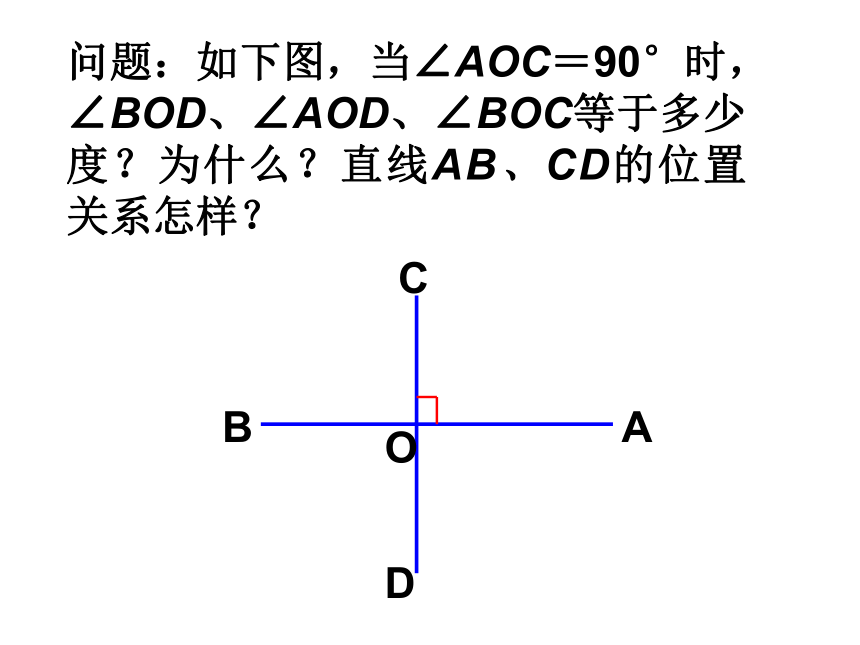
课件19张PPT。5.1.2 垂线(1)在相交线的模型中,固定木条a,转动木条b,当α =90°时,a与b垂直.当b的位置变化时,a、b所成的角α也会发生变化.当α ≠90°时,a与b不垂直,叫斜交.两条直线相交斜交垂直垂直是相交的特殊情况观察思考)α abbbbb)α 问题:如下图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC等于多少度?为什么?直线AB、CD的位置关系怎样?
问题:什么样的两条直线互相垂直? 定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
对垂线定义的理解:(1)在垂直的定义中,只要一个角是直角就可以了,而不必说四个角都是直角,因为其他三个角是直角都可以由一个角是直角推出。(2)两条直线垂直,是对两条直线而言的,因此说到垂线一定是两条直线的位置关系 垂直的记法、读法
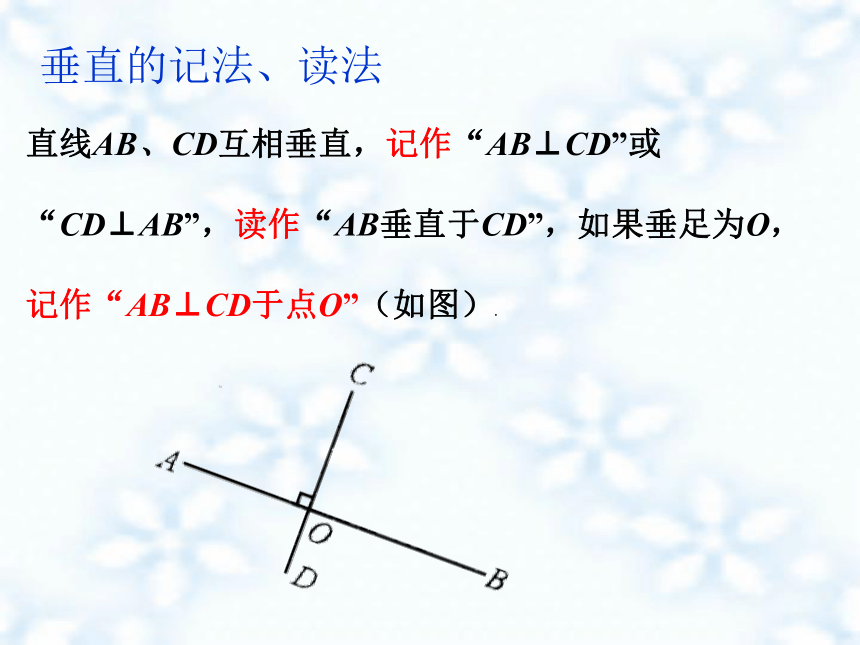
直线AB、CD互相垂直,记作“AB⊥CD”或
“CD⊥AB”,读作“AB垂直于CD”,如果垂足为O,
记作“AB⊥CD于点O”(如图).
垂直的定义的含义 ∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°(或三个角中的一个角等于90°),那么 AB⊥CD.这个推理过程可以写成: ∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:CDOAB生活中的垂直选择题:
1、 两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是
(A) 有两个角相等 ( B)有两对角相等
(C) 有三个角相等 ( D) 有四对邻补角
(C)2、下面四种判定两条直线的垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
( A) 4 (B) 3
(C) 2 (D) 1A画一画画一条直线的垂线,这样的垂线能画多少条?
过直线上一点作已知直线的垂线,这样的垂线能画多少条?
过直线外一点作已知直线的垂线,这样的垂线能画多少条?(无数条)(一条)(一条)根据以上的结果,你能得出什么结论?垂线的第一性质:过一点有且只有一条直线与已知直线
垂直。 (1)“有且只有”中,“有”指存在,“只有”
指唯一性。
(2)“过一点”中的点,可以在已知直线上,也
可以在已知直线外。注意:过一点画出已知直线的垂线 D一贴二靠1.贴住 已知 直线 2. 靠住 已知点画法: 3.画垂线 标垂足三画结论:则直线DA即为所求垂线。例1:在图中,过点A分别作BD和DE的垂线.NM结论:直线AM,AN为所求垂线。课堂练习1.选择题
C课堂练习(教科书第5页的练习):
2. 过点P作线段或射线所在直线的垂线3.过点P分别向角的两边作垂线例2:按要求画图:ABCABCABC(1)过B点作AC的垂线; (2)过A点作BC的垂线; (3)过C点作AB的垂线。结论:略。两条直线相交一般情况垂线对顶角:相等邻补角:互补垂线的存在性和唯一性
特殊情况相交成直角小 结1.垂线的定义2.过一点作一条直线的垂线3.垂线的第一性质
问题:什么样的两条直线互相垂直? 定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
对垂线定义的理解:(1)在垂直的定义中,只要一个角是直角就可以了,而不必说四个角都是直角,因为其他三个角是直角都可以由一个角是直角推出。(2)两条直线垂直,是对两条直线而言的,因此说到垂线一定是两条直线的位置关系 垂直的记法、读法
直线AB、CD互相垂直,记作“AB⊥CD”或
“CD⊥AB”,读作“AB垂直于CD”,如果垂足为O,
记作“AB⊥CD于点O”(如图).
垂直的定义的含义 ∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°(或三个角中的一个角等于90°),那么 AB⊥CD.这个推理过程可以写成: ∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:CDOAB生活中的垂直选择题:
1、 两条直线相交所成的四个角中,下列条件中能判
定两条直线垂直的是
(A) 有两个角相等 ( B)有两对角相等
(C) 有三个角相等 ( D) 有四对邻补角
(C)2、下面四种判定两条直线的垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
( A) 4 (B) 3
(C) 2 (D) 1A画一画画一条直线的垂线,这样的垂线能画多少条?
过直线上一点作已知直线的垂线,这样的垂线能画多少条?
过直线外一点作已知直线的垂线,这样的垂线能画多少条?(无数条)(一条)(一条)根据以上的结果,你能得出什么结论?垂线的第一性质:过一点有且只有一条直线与已知直线
垂直。 (1)“有且只有”中,“有”指存在,“只有”
指唯一性。
(2)“过一点”中的点,可以在已知直线上,也
可以在已知直线外。注意:过一点画出已知直线的垂线 D一贴二靠1.贴住 已知 直线 2. 靠住 已知点画法: 3.画垂线 标垂足三画结论:则直线DA即为所求垂线。例1:在图中,过点A分别作BD和DE的垂线.NM结论:直线AM,AN为所求垂线。课堂练习1.选择题
C课堂练习(教科书第5页的练习):
2. 过点P作线段或射线所在直线的垂线3.过点P分别向角的两边作垂线例2:按要求画图:ABCABCABC(1)过B点作AC的垂线; (2)过A点作BC的垂线; (3)过C点作AB的垂线。结论:略。两条直线相交一般情况垂线对顶角:相等邻补角:互补垂线的存在性和唯一性
特殊情况相交成直角小 结1.垂线的定义2.过一点作一条直线的垂线3.垂线的第一性质
