5.1.2垂线(2)(浙江省台州市)
文档属性
| 名称 | 5.1.2垂线(2)(浙江省台州市) |
|
|
| 格式 | rar | ||
| 文件大小 | 114.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-02-25 00:00:00 | ||
图片预览


文档简介
课件16张PPT。 5.1.2垂线(二)知识回顾1、直线相交时有几种情况?2、怎样的两条直线我们称它们互相垂直?3、一条直线仅有一条垂线。对吗?斜交与垂直结论: 过一点有且只有一条直线与已知直线垂直.m问题:有人不慎掉入有鳄鱼的湖中。如图,他在P点,
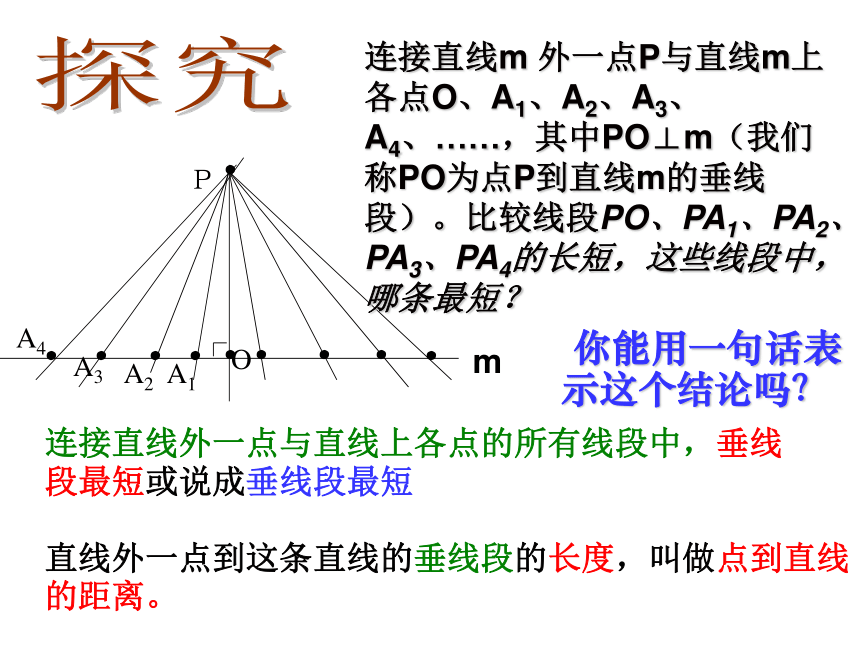
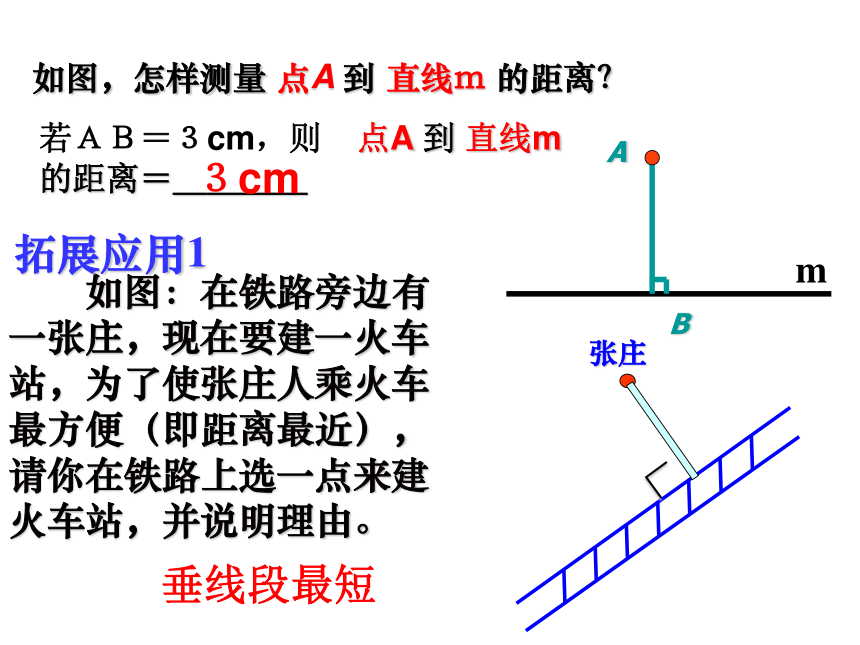
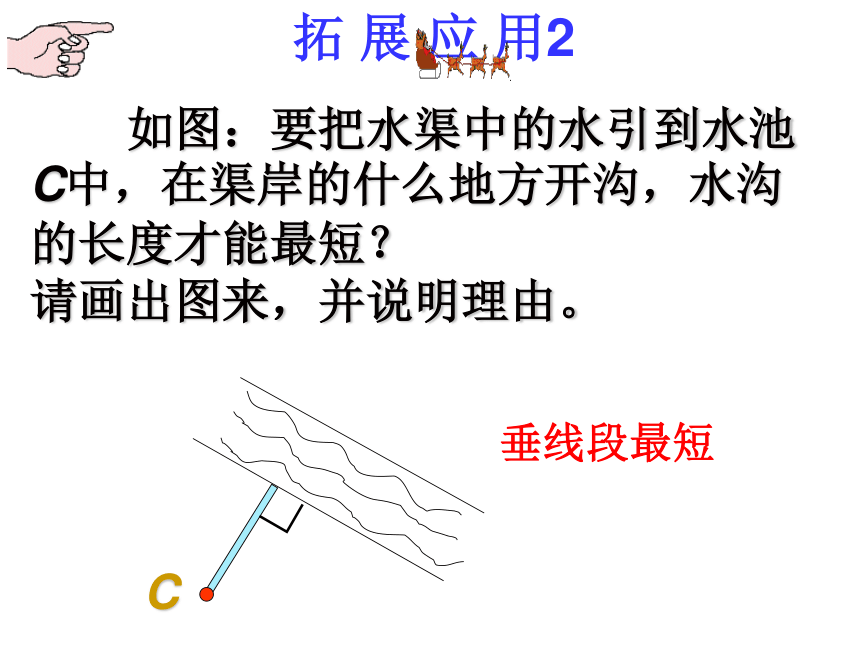
应选择什么样的路线尽快游到岸边m呢?探究.P.........OA1A2A3A4连接直线外一点与直线上各点的所有线段中,垂线段最短或说成垂线段最短直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。连接直线m 外一点P与直线m上各点O、A1、A2、A3、A4、……,其中PO⊥m(我们称PO为点P到直线m的垂线段)。比较线段PO、PA1、PA2、PA3、PA4的长短,这些线段中,哪条最短?m 你能用一句话表示这个结论吗?B如图,怎样测量 点A 到 直线m 的距离? 如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。张庄拓展应用1m若AB=3cm,则 点A 到 直线m 的距离=____3cm垂线段最短拓 展 应 用2 如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
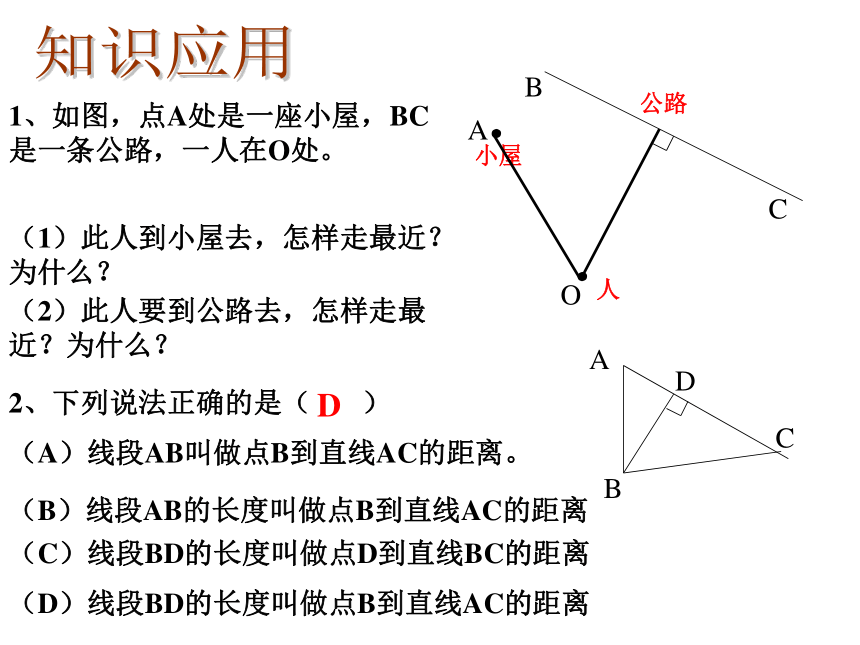
请画出图来,并说明理由。C∟垂线段最短知识应用1、如图,点A处是一座小屋,BC是一条公路,一人在O处。(1)此人到小屋去,怎样走最近?为什么?(2)此人要到公路去,怎样走最近?为什么?2、下列说法正确的是( )BC小屋公路人D 3、如图所示,在△ABC中,∠ABC=90 ,BD⊥AC,DE⊥AB,则
点A到直线BC的距离是线段 的长度.
点B到直线AC的距离是线段 的长度.
点D到直线AB的距离是线段 的长度
线段AD的长度是点 到直线 的距离.ABBDDEABD例1、如图,点M、N分别在直线AB、CD上,用三角板画图, 1)过M点画CD的垂线交CD于F点, 2)M点和N点的距离是线段____的长, 3)M点到CD的距离是线段____的长。MNMFABCDMN∴直线MF为所求垂线。AB答:……。 例2、如图,量出(1)村庄A与货场B的距离,(2)货场B到铁道的距离。立定跳远中,体育老师是如何测量运动员的成绩的?体育老师实际上测量的是点到直线的距离
书本P9页第10题例3选择题:2.如图, AC⊥BC, ∠C=900 ,线段AC、BC、CD中最短的是( )
(A) AC (B) BC (C) CD (D) 不能确定1、已知点A,与点A的距离是5cm的直线可画( )
A. 1条 B. 2条 C. 3条 D. 无数条DABCDC3、点P为直线m外一点,点A、B、C为直线m 上的三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A、4cm B、2cm
C、小于2cm D、不大于2cm4、如图,三角形ABC中,∠C=90°,三角形ABC的三条边AB、BC、AC哪条边最长?为什么?如图(1)找出线段BC的中点M,连接AM
(2)过B、C两点分别作AM的垂线段,
垂足是D、E
(3)比较BD和CE的大小
ABCDGM· · 问题1:长方体的顶点A处有一只蚂蚁想爬到点C处,请你帮它画出爬行的最佳路线。并说明理由。 问题2:若A处的蚂蚁想爬到棱BC上,你认为它的最佳路线是什么?并说明理由。
问题3:若蚂蚁在点M处,想爬到棱BC上,请你设计一条最佳路线。并说明理由。
┏
N如图:AC⊥BC于C,CD⊥AB于D,DE⊥BC于E,试比较四条线段AB 、AC、DC和 DE的大小。CADEB解:∵ AC⊥BC于C(已知)∴ AC<AB(垂线段最短)又∵ CD⊥AD于D(已知)∵ DE⊥BC于E(已知)∴ CD<AC(垂线段最短)∴ DE<CD(垂线段最短)∴ AB>AC>CD>DE拓展提高
应选择什么样的路线尽快游到岸边m呢?探究.P.........OA1A2A3A4连接直线外一点与直线上各点的所有线段中,垂线段最短或说成垂线段最短直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。连接直线m 外一点P与直线m上各点O、A1、A2、A3、A4、……,其中PO⊥m(我们称PO为点P到直线m的垂线段)。比较线段PO、PA1、PA2、PA3、PA4的长短,这些线段中,哪条最短?m 你能用一句话表示这个结论吗?B如图,怎样测量 点A 到 直线m 的距离? 如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。张庄拓展应用1m若AB=3cm,则 点A 到 直线m 的距离=____3cm垂线段最短拓 展 应 用2 如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。C∟垂线段最短知识应用1、如图,点A处是一座小屋,BC是一条公路,一人在O处。(1)此人到小屋去,怎样走最近?为什么?(2)此人要到公路去,怎样走最近?为什么?2、下列说法正确的是( )BC小屋公路人D 3、如图所示,在△ABC中,∠ABC=90 ,BD⊥AC,DE⊥AB,则
点A到直线BC的距离是线段 的长度.
点B到直线AC的距离是线段 的长度.
点D到直线AB的距离是线段 的长度
线段AD的长度是点 到直线 的距离.ABBDDEABD例1、如图,点M、N分别在直线AB、CD上,用三角板画图, 1)过M点画CD的垂线交CD于F点, 2)M点和N点的距离是线段____的长, 3)M点到CD的距离是线段____的长。MNMFABCDMN∴直线MF为所求垂线。AB答:……。 例2、如图,量出(1)村庄A与货场B的距离,(2)货场B到铁道的距离。立定跳远中,体育老师是如何测量运动员的成绩的?体育老师实际上测量的是点到直线的距离
书本P9页第10题例3选择题:2.如图, AC⊥BC, ∠C=900 ,线段AC、BC、CD中最短的是( )
(A) AC (B) BC (C) CD (D) 不能确定1、已知点A,与点A的距离是5cm的直线可画( )
A. 1条 B. 2条 C. 3条 D. 无数条DABCDC3、点P为直线m外一点,点A、B、C为直线m 上的三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A、4cm B、2cm
C、小于2cm D、不大于2cm4、如图,三角形ABC中,∠C=90°,三角形ABC的三条边AB、BC、AC哪条边最长?为什么?如图(1)找出线段BC的中点M,连接AM
(2)过B、C两点分别作AM的垂线段,
垂足是D、E
(3)比较BD和CE的大小
ABCDGM· · 问题1:长方体的顶点A处有一只蚂蚁想爬到点C处,请你帮它画出爬行的最佳路线。并说明理由。 问题2:若A处的蚂蚁想爬到棱BC上,你认为它的最佳路线是什么?并说明理由。
问题3:若蚂蚁在点M处,想爬到棱BC上,请你设计一条最佳路线。并说明理由。
┏
N如图:AC⊥BC于C,CD⊥AB于D,DE⊥BC于E,试比较四条线段AB 、AC、DC和 DE的大小。CADEB解:∵ AC⊥BC于C(已知)∴ AC<AB(垂线段最短)又∵ CD⊥AD于D(已知)∵ DE⊥BC于E(已知)∴ CD<AC(垂线段最短)∴ DE<CD(垂线段最短)∴ AB>AC>CD>DE拓展提高
