2023-2024学年人教版八年级数学上册 第十一章 三角形 章末测试卷(一) (含解析)
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册 第十一章 三角形 章末测试卷(一) (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 244.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-04 19:09:22 | ||
图片预览

文档简介
第十一章 三角形 章末测试卷(一)
一.选择题(共10小题)
1.下列长度的三条线段能组成三角形的是( )
A.6,2,3 B.3,3,3 C.4,3,8 D.4,3,7
2.若△ABC的三个内角之比为2:3:5,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.现有两根长度分别这3cm和6cm的木棒,若要钉成一个三角形木棒,则第三根木棒长可以为( )
A.2cm B.3cm C.5cm D.9cm
4.人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.两直线平行,内错角相等
D.三角形具有稳定性
5.正五边形的外角和的度数( )
A.180° B.72° C.540° D.360°
6.若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )
A.60° B.50° C.40° D.30°
7.一个多边形的内角和等于540°,则它的边数为( )
A.4 B.5 C.6 D.8
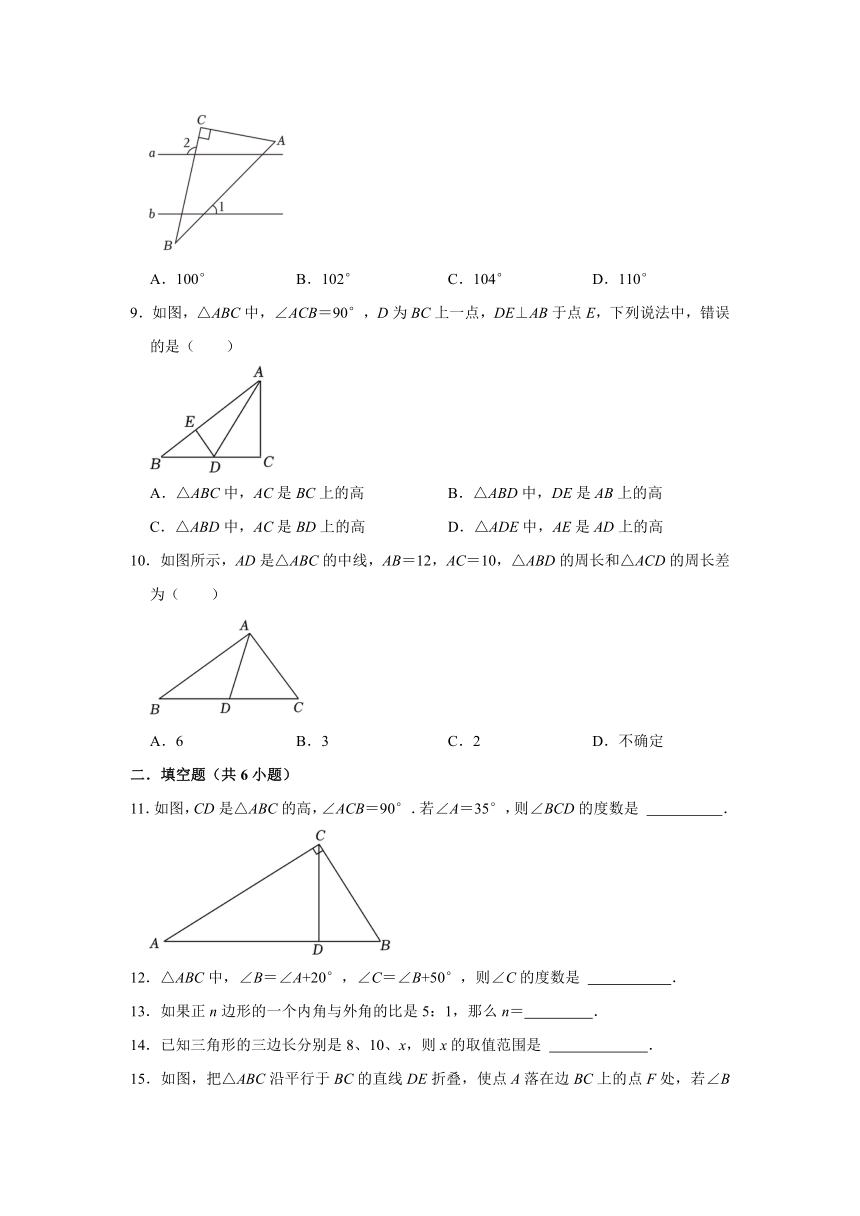
8.如图,直线a∥b,将含30°角的直角三角板ABC(∠B=30° )按图中位置摆放,若∠1=48°,则∠2的度数为( )
A.100° B.102° C.104° D.110°
9.如图,△ABC中,∠ACB=90°,D为BC上一点,DE⊥AB于点E,下列说法中,错误的是( )
A.△ABC中,AC是BC上的高 B.△ABD中,DE是AB上的高
C.△ABD中,AC是BD上的高 D.△ADE中,AE是AD上的高
10.如图所示,AD是△ABC的中线,AB=12,AC=10,△ABD的周长和△ACD的周长差为( )
A.6 B.3 C.2 D.不确定
二.填空题(共6小题)
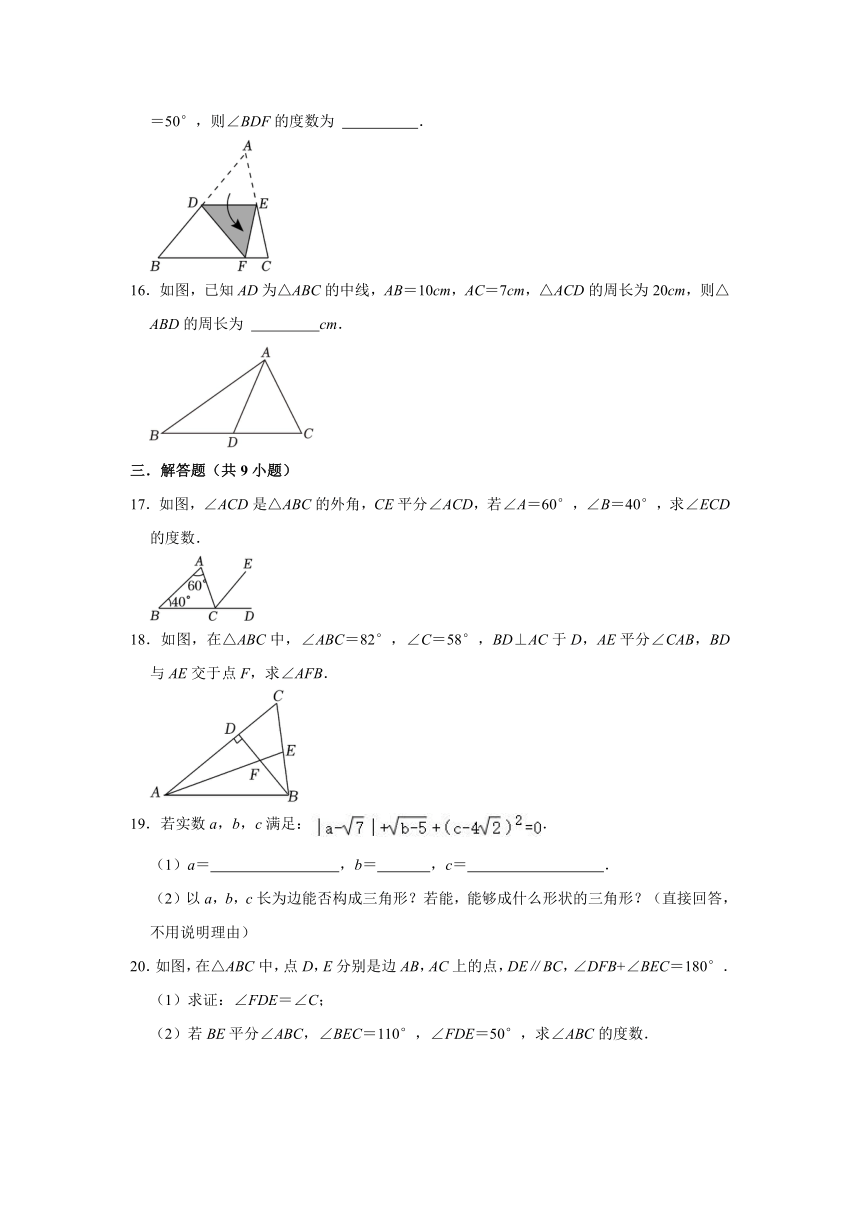
11.如图,CD是△ABC的高,∠ACB=90°.若∠A=35°,则∠BCD的度数是 .
12.△ABC中,∠B=∠A+20°,∠C=∠B+50°,则∠C的度数是 .
13.如果正n边形的一个内角与外角的比是5:1,那么n= .
14.已知三角形的三边长分别是8、10、x,则x的取值范围是 .
15.如图,把△ABC沿平行于BC的直线DE折叠,使点A落在边BC上的点F处,若∠B=50°,则∠BDF的度数为 .
16.如图,已知AD为△ABC的中线,AB=10cm,AC=7cm,△ACD的周长为20cm,则△ABD的周长为 cm.
三.解答题(共9小题)
17.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,求∠ECD的度数.
18.如图,在△ABC中,∠ABC=82°,∠C=58°,BD⊥AC于D,AE平分∠CAB,BD与AE交于点F,求∠AFB.
19.若实数a,b,c满足:.
(1)a= ,b= ,c= .
(2)以a,b,c长为边能否构成三角形?若能,能够成什么形状的三角形?(直接回答,不用说明理由)
20.如图,在△ABC中,点D,E分别是边AB,AC上的点,DE∥BC,∠DFB+∠BEC=180°.
(1)求证:∠FDE=∠C;
(2)若BE平分∠ABC,∠BEC=110°,∠FDE=50°,求∠ABC的度数.
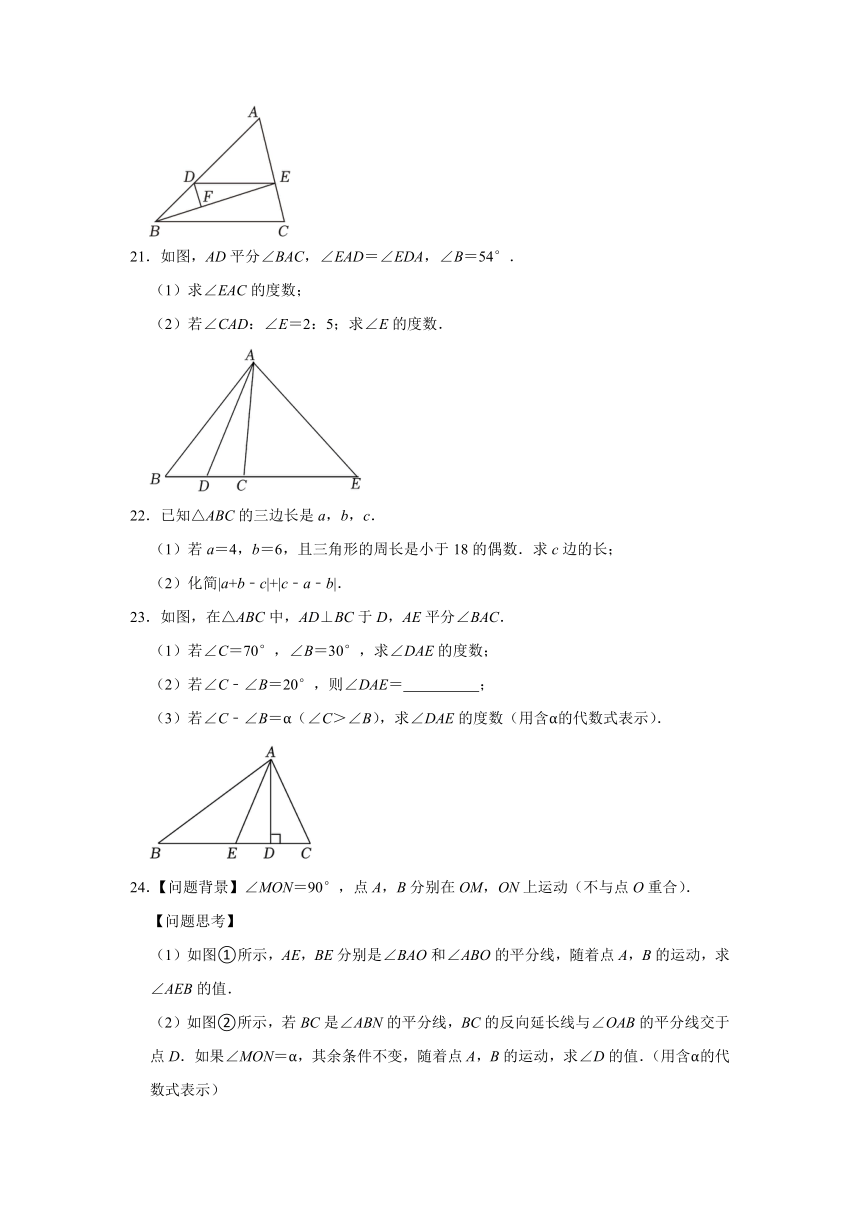
21.如图,AD平分∠BAC,∠EAD=∠EDA,∠B=54°.
(1)求∠EAC的度数;
(2)若∠CAD:∠E=2:5;求∠E的度数.
22.已知△ABC的三边长是a,b,c.
(1)若a=4,b=6,且三角形的周长是小于18的偶数.求c边的长;
(2)化简|a+b﹣c|+|c﹣a﹣b|.
23.如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=30°,求∠DAE的度数;
(2)若∠C﹣∠B=20°,则∠DAE= ;
(3)若∠C﹣∠B=α(∠C>∠B),求∠DAE的度数(用含α的代数式表示).
24.【问题背景】∠MON=90°,点A,B分别在OM,ON上运动(不与点O重合).
【问题思考】
(1)如图①所示,AE,BE分别是∠BAO和∠ABO的平分线,随着点A,B的运动,求∠AEB的值.
(2)如图②所示,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.如果∠MON=α,其余条件不变,随着点A,B的运动,求∠D的值.(用含α的代数式表示)
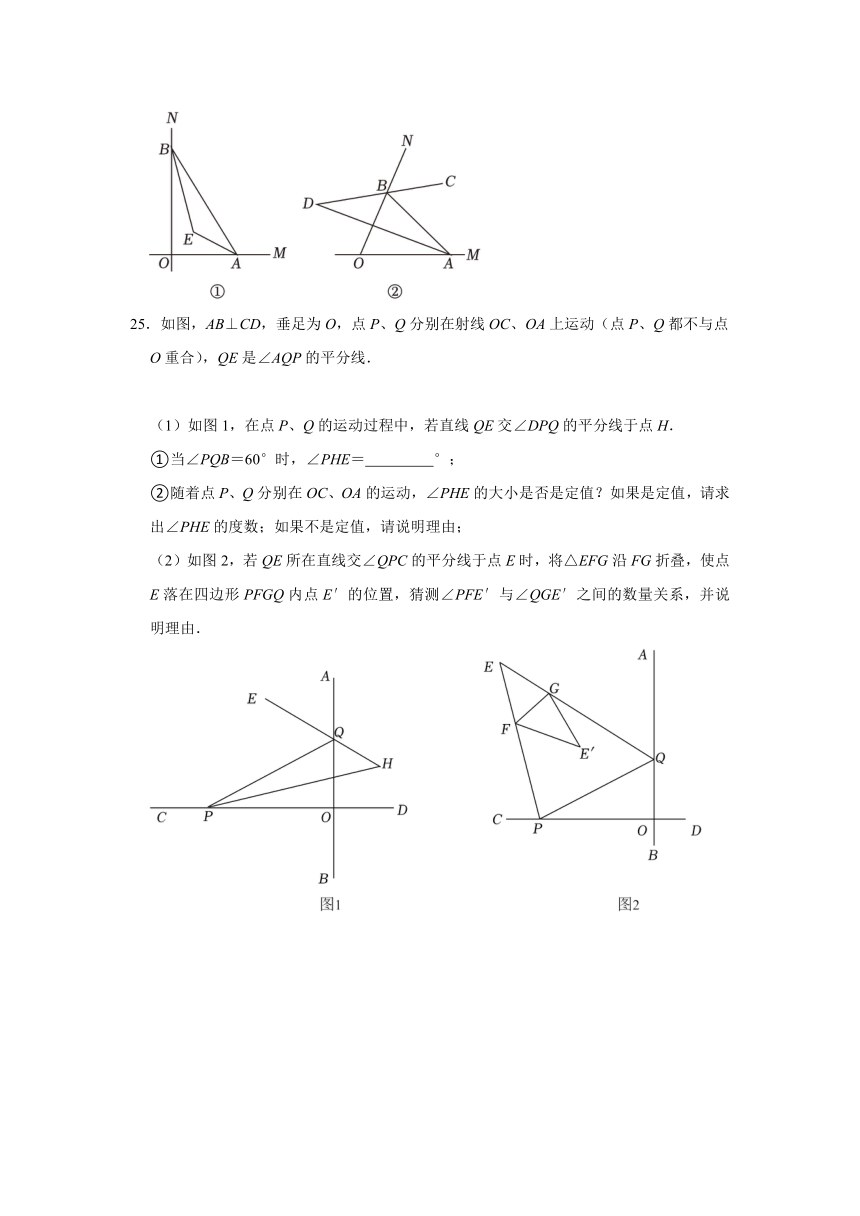
25.如图,AB⊥CD,垂足为O,点P、Q分别在射线OC、OA上运动(点P、Q都不与点O重合),QE是∠AQP的平分线.
(1)如图1,在点P、Q的运动过程中,若直线QE交∠DPQ的平分线于点H.
①当∠PQB=60°时,∠PHE= °;
②随着点P、Q分别在OC、OA的运动,∠PHE的大小是否是定值?如果是定值,请求出∠PHE的度数;如果不是定值,请说明理由;
(2)如图2,若QE所在直线交∠QPC的平分线于点E时,将△EFG沿FG折叠,使点E落在四边形PFGQ内点E′的位置,猜测∠PFE′与∠QGE′之间的数量关系,并说明理由.
第十一章 三角形 章末测试卷(一)
参考答案与试题解析
一.选择题(共10小题)
1.下列长度的三条线段能组成三角形的是( )
A.6,2,3 B.3,3,3 C.4,3,8 D.4,3,7
【解答】解:A、∵2+3<6,
∴6,2,3不能构成三角形,不符合题意;
B、∵3﹣3<3<3+3,即0<3<6,
∴3,3,3能构成三角形,符合题意;
C、∵4+3<8,
∴4,3,8不能构成三角形,不符合题意;
D、∵4+3=7,
∴4,3,7不能构成三角形,不符合题意.
故选:B.
2.若△ABC的三个内角之比为2:3:5,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
【解答】解:∵△ABC的三个内角的比为2:3:5可设此三角形的三个内角分别为2x°,3x°,5x°,
∴2x°+3x°+5x°=180°,
解得x=18°,
∴5x°=5×18°=90°.
∴此三角形是直角三角形.
故选:B.
3.现有两根长度分别这3cm和6cm的木棒,若要钉成一个三角形木棒,则第三根木棒长可以为( )
A.2cm B.3cm C.5cm D.9cm
【解答】解:设第三根木棒长为xcm,
则6﹣3<x<6+3,即3<x<9,
∴四个选项中,第三根木棒长可以为5cm,
故选:C.
4.人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.两直线平行,内错角相等
D.三角形具有稳定性
【解答】解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:D.
5.正五边形的外角和的度数( )
A.180° B.72° C.540° D.360°
【解答】解:任意多边形的外角和都是360°,
故正五边形的外角和的度数为360°.
故选:D.
6.若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )
A.60° B.50° C.40° D.30°
【解答】解:∵直角三角形中两锐角互余,
∴若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是90°﹣40°=50°.
故选:B.
7.一个多边形的内角和等于540°,则它的边数为( )
A.4 B.5 C.6 D.8
【解答】解:设这个多边形的边数为n,
∴(n﹣2) 180°=540°,
∴n=5.
故选:B.
8.如图,直线a∥b,将含30°角的直角三角板ABC(∠B=30° )按图中位置摆放,若∠1=48°,则∠2的度数为( )
A.100° B.102° C.104° D.110°
【解答】解:如图所示,
∵a∥b,
∴∠1=∠3=48°,
∵∠4+∠3+∠B=180°,
∴∠4=102°,
∴∠2=∠3=102°.
故选:B.
9.如图,△ABC中,∠ACB=90°,D为BC上一点,DE⊥AB于点E,下列说法中,错误的是( )
A.△ABC中,AC是BC上的高 B.△ABD中,DE是AB上的高
C.△ABD中,AC是BD上的高 D.△ADE中,AE是AD上的高
【解答】解:A、△ABC中,AC是BC上的高,说法正确,不符合题意;
B、△ABD中,DE是AB上的高,说法正确,不符合题意;
C、△ABD中,AC是BD上的高,说法正确,不符合题意;
D、△ADE中,AE是DE上的高,不是AD上的高,故本选项说法错误,符合题意;
故选:D.
10.如图所示,AD是△ABC的中线,AB=12,AC=10,△ABD的周长和△ACD的周长差为( )
A.6 B.3 C.2 D.不确定
【解答】解:∵AD是△ABC的中线,
∴BD=DC,
∵AB=12,AC=10,
∴(AB+BD+AD)﹣(AC+CD+AD)
=AB﹣AC
=12﹣10
=2,
∴△ABD的周长和△ACD的周长差为2,
故选:C.
二.填空题(共6小题)
11.如图,CD是△ABC的高,∠ACB=90°.若∠A=35°,则∠BCD的度数是 35° .
【解答】解:∵CD是△ABC的高,
∴CD⊥AB,
∴∠ADC=90°,
∵在△ACD中,∠A+∠ADC+∠ACD=180°,∠A=35°,∠ACB=90°,
∴∠ACD=55°
∵∠ACB=∠ACD+∠BCD=90°,
∴∠BCD=35°.
故答案为:35°.
12.△ABC中,∠B=∠A+20°,∠C=∠B+50°,则∠C的度数是 100° .
【解答】解:∵∠B=∠A+20°,∠C=∠B+50°,
∴∠C=∠A+20°+50°=∠A+70°,
又∵∠A+∠B+∠C=180°,
∴∠A+∠A+20°+∠A+70°=180°,
∴∠A=30°,
∴∠C=∠A+70°=30°+70°=100°.
故答案为:100°.
13.如果正n边形的一个内角与外角的比是5:1,那么n= 12 .
【解答】解:∵正n边形的一个内角与外角的比是5:1,
设外角的度数为x,则内角的度数为5x,
∴x+5x=180,
解得x=30,
故,
故答案为:12.
14.已知三角形的三边长分别是8、10、x,则x的取值范围是 2<x<18 .
【解答】解:根据三角形的三边关系可得:10﹣8<x<10+8,
即2<x<18,
故答案为:2<x<18.
15.如图,把△ABC沿平行于BC的直线DE折叠,使点A落在边BC上的点F处,若∠B=50°,则∠BDF的度数为 80° .
【解答】解:∵DE∥BC,
∴∠ADE=∠B=50°.
由折叠的性质可知:∠FDE=∠ADE=50°,
∴∠BDF=180°﹣∠ADE﹣∠FDE=180°﹣50°﹣50°=80°.
故答案为:80°.
16.如图,已知AD为△ABC的中线,AB=10cm,AC=7cm,△ACD的周长为20cm,则△ABD的周长为 23 cm.
【解答】解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC=10﹣7=3(cm),
∵△ACD的周长为20cm,AB比AC长3cm,
∴△ABD周长为:20+3=23(cm).
故答案为23.
三.解答题(共9小题)
17.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,求∠ECD的度数.
【解答】解:由三角形的外角可知,∠ACD=∠A+∠B=100°,
∵CE平分∠ACD,
∴∠ECD=∠ACD=50°.
18.如图,在△ABC中,∠ABC=82°,∠C=58°,BD⊥AC于D,AE平分∠CAB,BD与AE交于点F,求∠AFB.
【解答】解:∵∠CAB=180°﹣∠ABC﹣∠C,
而∠ABC=82°,∠C=58°,
∴∠CAB=40°,
∵AE平分∠CAB,
∴∠DAF=20°,
∵BD⊥AC于D,
∴∠ADB=90°,
∴∠AFB=∠ADB+∠DAF=90°+20°=110°.
故答案为:110°.
19.若实数a,b,c满足:.
(1)a= ,b= 5 ,c= 4 .
(2)以a,b,c长为边能否构成三角形?若能,能够成什么形状的三角形?(直接回答,不用说明理由)
【解答】解:(1)根据题意得:a﹣=0,b﹣5=0,c﹣4=0,
解得:a=,b=5,c=4;
故答案为:;5;4;
(2)∵()2+52=(4)2,
∴a2+b2=c2,
∴以a、b、c为边能构成三角形,构成的三角形是直角三角形.
20.如图,在△ABC中,点D,E分别是边AB,AC上的点,DE∥BC,∠DFB+∠BEC=180°.
(1)求证:∠FDE=∠C;
(2)若BE平分∠ABC,∠BEC=110°,∠FDE=50°,求∠ABC的度数.
【解答】(1)证明:∵DE∥BC,
∴∠DEF=∠CBE,
∵∠DFB+∠BEC=180°,∠DFB+∠EFD=180°,
∴∠BEC=∠EFD,
又∵∠FDE=180°﹣∠DEF﹣∠EFD,∠C=180°﹣∠CBE﹣∠BEC,
∴∠FDE=∠C;
(2)解:∵∠FDE=∠C,∠FDE=50°,
∴∠C=50°.
在△BCE中,∠C=50°,∠BEC=110°,
∴∠CBE=180°﹣∠C﹣∠BEC=180°﹣50°﹣110°=20°,
又∵BE平分∠ABC,
∴∠ABC=2∠CBE=2×20°=40°.
21.如图,AD平分∠BAC,∠EAD=∠EDA,∠B=54°.
(1)求∠EAC的度数;
(2)若∠CAD:∠E=2:5;求∠E的度数.
【解答】解:(1)∵∠EAD=∠EDA,
∴∠EAC+∠CAD=∠B+∠BAD,
∵AD平分∠BAC,
∴∠CAD=∠BAD.
∴∠EAC=∠B.
∵∠B=54°,
∴∠EAC=54°.
(2)设∠CAD=2x,则∠E=5x,∠DAB=2x,
∵∠B=54°,
∴∠EDA=∠EAD=2x+54°.
∵∠EDA+∠EAD+∠E=180°,
∴2x+54°+2x+54°+5x=180°.
解得x=8°.
∴∠E=5x=40°.
22.已知△ABC的三边长是a,b,c.
(1)若a=4,b=6,且三角形的周长是小于18的偶数.求c边的长;
(2)化简|a+b﹣c|+|c﹣a﹣b|.
【解答】解:(1)∵a,b,c是△ABC的三边,a=4,b=6,
∴2<c<10,
∵三角形的周长是小于18的偶数,
∴2<c<8,
∴c=4或6;
(2)|a+b﹣c|+|c﹣a﹣b|
=a+b﹣c﹣c+a+b
=2a+2b﹣2c.
23.如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=30°,求∠DAE的度数;
(2)若∠C﹣∠B=20°,则∠DAE= 10° ;
(3)若∠C﹣∠B=α(∠C>∠B),求∠DAE的度数(用含α的代数式表示).
【解答】解:∵AD⊥BC于D,AE平分∠BAC.
∴∠ADC=∠ADB=90°,∠BAE=∠CAE=BAC.
(1)∵∠C=70°,∠B=30°,
∴∠BAC=180°﹣∠B﹣∠C=80°,∠CAD=90°﹣∠C=20°.
∴∠DAE=∠CAE﹣∠CAD
=∠BAC﹣∠CAD
=×80°﹣20°
=20°;
(2)∵∠BAC=180°﹣∠B﹣∠C,∠CAD=90°﹣∠C,
∴∠DAE=∠CAE﹣∠CAD
=∠BAC﹣∠CAD
=(180°﹣∠B﹣∠C)﹣(90°﹣∠C)
=90°﹣∠B﹣∠C﹣90°+∠C
=∠C﹣∠B
=(∠C﹣∠B).
∵∠C﹣∠B=20°,
∴∠DAE=×20°=10°.
故答案为:10°.
(3)∵∠BAC=180°﹣∠B﹣∠C,∠CAD=90°﹣∠C,
∴∠DAE=∠CAE﹣∠CAD
=∠BAC﹣∠CAD
=(180°﹣∠B﹣∠C)﹣(90°﹣∠C)
=90°﹣∠B﹣∠C﹣90°+∠C
=∠C﹣∠B
=(∠C﹣∠B).
∵∠C﹣∠B=α,
∴∠DAE=×a=.
24.【问题背景】∠MON=90°,点A,B分别在OM,ON上运动(不与点O重合).
【问题思考】
(1)如图①所示,AE,BE分别是∠BAO和∠ABO的平分线,随着点A,B的运动,求∠AEB的值.
(2)如图②所示,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.如果∠MON=α,其余条件不变,随着点A,B的运动,求∠D的值.(用含α的代数式表示)
【解答】解:(1)∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=∠OAB,∠ABE=∠ABO,
∴∠BAE+∠ABE=(∠OAB+∠ABO)=45°,
∴∠AEB=135°;
(2)设∠BAD=x,
∵AD平分∠BAO,
∴∠BAO=2x,
∵∠AOB=α
∴∠ABN=180°﹣∠ABO=∠AOB+∠BAO=α+2x.
∵BC平分∠ABN,
∴,,
∵∠ABC=180°﹣∠ABD=∠D+∠BAD.
∴,
25.如图,AB⊥CD,垂足为O,点P、Q分别在射线OC、OA上运动(点P、Q都不与点O重合),QE是∠AQP的平分线.
(1)如图1,在点P、Q的运动过程中,若直线QE交∠DPQ的平分线于点H.
①当∠PQB=60°时,∠PHE= 45 °;
②随着点P、Q分别在OC、OA的运动,∠PHE的大小是否是定值?如果是定值,请求出∠PHE的度数;如果不是定值,请说明理由;
(2)如图2,若QE所在直线交∠QPC的平分线于点E时,将△EFG沿FG折叠,使点E落在四边形PFGQ内点E′的位置,猜测∠PFE′与∠QGE′之间的数量关系,并说明理由.
【解答】解:(1)①∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠PQB=60°,
∴∠QPO=30°,∠AQP=120°,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°,
故答案为:45;
②∠PHE 是一个定值,∠PHE=45°,理由如下:
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∴∠QPO=90°﹣∠PQO,∠AQP=180°﹣∠PQO,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°;
(2)∠PFE'+∠QGE'=90°,理由如下:
如图2所示,连接EE',
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠CPQ+∠QPO=180°,∠PQA+∠PQO=180°,
∴180°﹣∠CPQ+180°﹣∠PQA=90°,
∴∠CPQ+∠PQA=270°,
∵QE,PE分别平分∠PQA,∠CPQ,
∴,
∴,
∴∠PEQ=180°﹣∠EPQ﹣∠EQP=45°,
由折叠的性质可知∠GE'F=∠PEQ=45°,
∵∠FEE'+∠EFE'+∠EE'F=180°=∠GEE'+∠EGE'+∠EE'G,
∴∠FEG+∠FE'G+∠EFE'+∠EGE'=360°,
∴∠EFE'+∠EFE'=270°,
∵∠EFE'+∠PFE'=180°=∠EGE'+∠QGE',
∴∠PFE'+∠QGE'=360°﹣∠EFE'﹣∠EFE'=90°.
一.选择题(共10小题)
1.下列长度的三条线段能组成三角形的是( )
A.6,2,3 B.3,3,3 C.4,3,8 D.4,3,7
2.若△ABC的三个内角之比为2:3:5,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.现有两根长度分别这3cm和6cm的木棒,若要钉成一个三角形木棒,则第三根木棒长可以为( )
A.2cm B.3cm C.5cm D.9cm
4.人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.两直线平行,内错角相等
D.三角形具有稳定性
5.正五边形的外角和的度数( )
A.180° B.72° C.540° D.360°
6.若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )
A.60° B.50° C.40° D.30°
7.一个多边形的内角和等于540°,则它的边数为( )
A.4 B.5 C.6 D.8
8.如图,直线a∥b,将含30°角的直角三角板ABC(∠B=30° )按图中位置摆放,若∠1=48°,则∠2的度数为( )
A.100° B.102° C.104° D.110°
9.如图,△ABC中,∠ACB=90°,D为BC上一点,DE⊥AB于点E,下列说法中,错误的是( )
A.△ABC中,AC是BC上的高 B.△ABD中,DE是AB上的高
C.△ABD中,AC是BD上的高 D.△ADE中,AE是AD上的高
10.如图所示,AD是△ABC的中线,AB=12,AC=10,△ABD的周长和△ACD的周长差为( )
A.6 B.3 C.2 D.不确定
二.填空题(共6小题)
11.如图,CD是△ABC的高,∠ACB=90°.若∠A=35°,则∠BCD的度数是 .
12.△ABC中,∠B=∠A+20°,∠C=∠B+50°,则∠C的度数是 .
13.如果正n边形的一个内角与外角的比是5:1,那么n= .
14.已知三角形的三边长分别是8、10、x,则x的取值范围是 .
15.如图,把△ABC沿平行于BC的直线DE折叠,使点A落在边BC上的点F处,若∠B=50°,则∠BDF的度数为 .
16.如图,已知AD为△ABC的中线,AB=10cm,AC=7cm,△ACD的周长为20cm,则△ABD的周长为 cm.
三.解答题(共9小题)
17.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,求∠ECD的度数.
18.如图,在△ABC中,∠ABC=82°,∠C=58°,BD⊥AC于D,AE平分∠CAB,BD与AE交于点F,求∠AFB.
19.若实数a,b,c满足:.
(1)a= ,b= ,c= .
(2)以a,b,c长为边能否构成三角形?若能,能够成什么形状的三角形?(直接回答,不用说明理由)
20.如图,在△ABC中,点D,E分别是边AB,AC上的点,DE∥BC,∠DFB+∠BEC=180°.
(1)求证:∠FDE=∠C;
(2)若BE平分∠ABC,∠BEC=110°,∠FDE=50°,求∠ABC的度数.
21.如图,AD平分∠BAC,∠EAD=∠EDA,∠B=54°.
(1)求∠EAC的度数;
(2)若∠CAD:∠E=2:5;求∠E的度数.
22.已知△ABC的三边长是a,b,c.
(1)若a=4,b=6,且三角形的周长是小于18的偶数.求c边的长;
(2)化简|a+b﹣c|+|c﹣a﹣b|.
23.如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=30°,求∠DAE的度数;
(2)若∠C﹣∠B=20°,则∠DAE= ;
(3)若∠C﹣∠B=α(∠C>∠B),求∠DAE的度数(用含α的代数式表示).
24.【问题背景】∠MON=90°,点A,B分别在OM,ON上运动(不与点O重合).
【问题思考】
(1)如图①所示,AE,BE分别是∠BAO和∠ABO的平分线,随着点A,B的运动,求∠AEB的值.
(2)如图②所示,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.如果∠MON=α,其余条件不变,随着点A,B的运动,求∠D的值.(用含α的代数式表示)
25.如图,AB⊥CD,垂足为O,点P、Q分别在射线OC、OA上运动(点P、Q都不与点O重合),QE是∠AQP的平分线.
(1)如图1,在点P、Q的运动过程中,若直线QE交∠DPQ的平分线于点H.
①当∠PQB=60°时,∠PHE= °;
②随着点P、Q分别在OC、OA的运动,∠PHE的大小是否是定值?如果是定值,请求出∠PHE的度数;如果不是定值,请说明理由;
(2)如图2,若QE所在直线交∠QPC的平分线于点E时,将△EFG沿FG折叠,使点E落在四边形PFGQ内点E′的位置,猜测∠PFE′与∠QGE′之间的数量关系,并说明理由.
第十一章 三角形 章末测试卷(一)
参考答案与试题解析
一.选择题(共10小题)
1.下列长度的三条线段能组成三角形的是( )
A.6,2,3 B.3,3,3 C.4,3,8 D.4,3,7
【解答】解:A、∵2+3<6,
∴6,2,3不能构成三角形,不符合题意;
B、∵3﹣3<3<3+3,即0<3<6,
∴3,3,3能构成三角形,符合题意;
C、∵4+3<8,
∴4,3,8不能构成三角形,不符合题意;
D、∵4+3=7,
∴4,3,7不能构成三角形,不符合题意.
故选:B.
2.若△ABC的三个内角之比为2:3:5,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
【解答】解:∵△ABC的三个内角的比为2:3:5可设此三角形的三个内角分别为2x°,3x°,5x°,
∴2x°+3x°+5x°=180°,
解得x=18°,
∴5x°=5×18°=90°.
∴此三角形是直角三角形.
故选:B.
3.现有两根长度分别这3cm和6cm的木棒,若要钉成一个三角形木棒,则第三根木棒长可以为( )
A.2cm B.3cm C.5cm D.9cm
【解答】解:设第三根木棒长为xcm,
则6﹣3<x<6+3,即3<x<9,
∴四个选项中,第三根木棒长可以为5cm,
故选:C.
4.人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.两直线平行,内错角相等
D.三角形具有稳定性
【解答】解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:D.
5.正五边形的外角和的度数( )
A.180° B.72° C.540° D.360°
【解答】解:任意多边形的外角和都是360°,
故正五边形的外角和的度数为360°.
故选:D.
6.若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )
A.60° B.50° C.40° D.30°
【解答】解:∵直角三角形中两锐角互余,
∴若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是90°﹣40°=50°.
故选:B.
7.一个多边形的内角和等于540°,则它的边数为( )
A.4 B.5 C.6 D.8
【解答】解:设这个多边形的边数为n,
∴(n﹣2) 180°=540°,
∴n=5.
故选:B.
8.如图,直线a∥b,将含30°角的直角三角板ABC(∠B=30° )按图中位置摆放,若∠1=48°,则∠2的度数为( )
A.100° B.102° C.104° D.110°
【解答】解:如图所示,
∵a∥b,
∴∠1=∠3=48°,
∵∠4+∠3+∠B=180°,
∴∠4=102°,
∴∠2=∠3=102°.
故选:B.
9.如图,△ABC中,∠ACB=90°,D为BC上一点,DE⊥AB于点E,下列说法中,错误的是( )
A.△ABC中,AC是BC上的高 B.△ABD中,DE是AB上的高
C.△ABD中,AC是BD上的高 D.△ADE中,AE是AD上的高
【解答】解:A、△ABC中,AC是BC上的高,说法正确,不符合题意;
B、△ABD中,DE是AB上的高,说法正确,不符合题意;
C、△ABD中,AC是BD上的高,说法正确,不符合题意;
D、△ADE中,AE是DE上的高,不是AD上的高,故本选项说法错误,符合题意;
故选:D.
10.如图所示,AD是△ABC的中线,AB=12,AC=10,△ABD的周长和△ACD的周长差为( )
A.6 B.3 C.2 D.不确定
【解答】解:∵AD是△ABC的中线,
∴BD=DC,
∵AB=12,AC=10,
∴(AB+BD+AD)﹣(AC+CD+AD)
=AB﹣AC
=12﹣10
=2,
∴△ABD的周长和△ACD的周长差为2,
故选:C.
二.填空题(共6小题)
11.如图,CD是△ABC的高,∠ACB=90°.若∠A=35°,则∠BCD的度数是 35° .
【解答】解:∵CD是△ABC的高,
∴CD⊥AB,
∴∠ADC=90°,
∵在△ACD中,∠A+∠ADC+∠ACD=180°,∠A=35°,∠ACB=90°,
∴∠ACD=55°
∵∠ACB=∠ACD+∠BCD=90°,
∴∠BCD=35°.
故答案为:35°.
12.△ABC中,∠B=∠A+20°,∠C=∠B+50°,则∠C的度数是 100° .
【解答】解:∵∠B=∠A+20°,∠C=∠B+50°,
∴∠C=∠A+20°+50°=∠A+70°,
又∵∠A+∠B+∠C=180°,
∴∠A+∠A+20°+∠A+70°=180°,
∴∠A=30°,
∴∠C=∠A+70°=30°+70°=100°.
故答案为:100°.
13.如果正n边形的一个内角与外角的比是5:1,那么n= 12 .
【解答】解:∵正n边形的一个内角与外角的比是5:1,
设外角的度数为x,则内角的度数为5x,
∴x+5x=180,
解得x=30,
故,
故答案为:12.
14.已知三角形的三边长分别是8、10、x,则x的取值范围是 2<x<18 .
【解答】解:根据三角形的三边关系可得:10﹣8<x<10+8,
即2<x<18,
故答案为:2<x<18.
15.如图,把△ABC沿平行于BC的直线DE折叠,使点A落在边BC上的点F处,若∠B=50°,则∠BDF的度数为 80° .
【解答】解:∵DE∥BC,
∴∠ADE=∠B=50°.
由折叠的性质可知:∠FDE=∠ADE=50°,
∴∠BDF=180°﹣∠ADE﹣∠FDE=180°﹣50°﹣50°=80°.
故答案为:80°.
16.如图,已知AD为△ABC的中线,AB=10cm,AC=7cm,△ACD的周长为20cm,则△ABD的周长为 23 cm.
【解答】解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC=10﹣7=3(cm),
∵△ACD的周长为20cm,AB比AC长3cm,
∴△ABD周长为:20+3=23(cm).
故答案为23.
三.解答题(共9小题)
17.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,求∠ECD的度数.
【解答】解:由三角形的外角可知,∠ACD=∠A+∠B=100°,
∵CE平分∠ACD,
∴∠ECD=∠ACD=50°.
18.如图,在△ABC中,∠ABC=82°,∠C=58°,BD⊥AC于D,AE平分∠CAB,BD与AE交于点F,求∠AFB.
【解答】解:∵∠CAB=180°﹣∠ABC﹣∠C,
而∠ABC=82°,∠C=58°,
∴∠CAB=40°,
∵AE平分∠CAB,
∴∠DAF=20°,
∵BD⊥AC于D,
∴∠ADB=90°,
∴∠AFB=∠ADB+∠DAF=90°+20°=110°.
故答案为:110°.
19.若实数a,b,c满足:.
(1)a= ,b= 5 ,c= 4 .
(2)以a,b,c长为边能否构成三角形?若能,能够成什么形状的三角形?(直接回答,不用说明理由)
【解答】解:(1)根据题意得:a﹣=0,b﹣5=0,c﹣4=0,
解得:a=,b=5,c=4;
故答案为:;5;4;
(2)∵()2+52=(4)2,
∴a2+b2=c2,
∴以a、b、c为边能构成三角形,构成的三角形是直角三角形.
20.如图,在△ABC中,点D,E分别是边AB,AC上的点,DE∥BC,∠DFB+∠BEC=180°.
(1)求证:∠FDE=∠C;
(2)若BE平分∠ABC,∠BEC=110°,∠FDE=50°,求∠ABC的度数.
【解答】(1)证明:∵DE∥BC,
∴∠DEF=∠CBE,
∵∠DFB+∠BEC=180°,∠DFB+∠EFD=180°,
∴∠BEC=∠EFD,
又∵∠FDE=180°﹣∠DEF﹣∠EFD,∠C=180°﹣∠CBE﹣∠BEC,
∴∠FDE=∠C;
(2)解:∵∠FDE=∠C,∠FDE=50°,
∴∠C=50°.
在△BCE中,∠C=50°,∠BEC=110°,
∴∠CBE=180°﹣∠C﹣∠BEC=180°﹣50°﹣110°=20°,
又∵BE平分∠ABC,
∴∠ABC=2∠CBE=2×20°=40°.
21.如图,AD平分∠BAC,∠EAD=∠EDA,∠B=54°.
(1)求∠EAC的度数;
(2)若∠CAD:∠E=2:5;求∠E的度数.
【解答】解:(1)∵∠EAD=∠EDA,
∴∠EAC+∠CAD=∠B+∠BAD,
∵AD平分∠BAC,
∴∠CAD=∠BAD.
∴∠EAC=∠B.
∵∠B=54°,
∴∠EAC=54°.
(2)设∠CAD=2x,则∠E=5x,∠DAB=2x,
∵∠B=54°,
∴∠EDA=∠EAD=2x+54°.
∵∠EDA+∠EAD+∠E=180°,
∴2x+54°+2x+54°+5x=180°.
解得x=8°.
∴∠E=5x=40°.
22.已知△ABC的三边长是a,b,c.
(1)若a=4,b=6,且三角形的周长是小于18的偶数.求c边的长;
(2)化简|a+b﹣c|+|c﹣a﹣b|.
【解答】解:(1)∵a,b,c是△ABC的三边,a=4,b=6,
∴2<c<10,
∵三角形的周长是小于18的偶数,
∴2<c<8,
∴c=4或6;
(2)|a+b﹣c|+|c﹣a﹣b|
=a+b﹣c﹣c+a+b
=2a+2b﹣2c.
23.如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=30°,求∠DAE的度数;
(2)若∠C﹣∠B=20°,则∠DAE= 10° ;
(3)若∠C﹣∠B=α(∠C>∠B),求∠DAE的度数(用含α的代数式表示).
【解答】解:∵AD⊥BC于D,AE平分∠BAC.
∴∠ADC=∠ADB=90°,∠BAE=∠CAE=BAC.
(1)∵∠C=70°,∠B=30°,
∴∠BAC=180°﹣∠B﹣∠C=80°,∠CAD=90°﹣∠C=20°.
∴∠DAE=∠CAE﹣∠CAD
=∠BAC﹣∠CAD
=×80°﹣20°
=20°;
(2)∵∠BAC=180°﹣∠B﹣∠C,∠CAD=90°﹣∠C,
∴∠DAE=∠CAE﹣∠CAD
=∠BAC﹣∠CAD
=(180°﹣∠B﹣∠C)﹣(90°﹣∠C)
=90°﹣∠B﹣∠C﹣90°+∠C
=∠C﹣∠B
=(∠C﹣∠B).
∵∠C﹣∠B=20°,
∴∠DAE=×20°=10°.
故答案为:10°.
(3)∵∠BAC=180°﹣∠B﹣∠C,∠CAD=90°﹣∠C,
∴∠DAE=∠CAE﹣∠CAD
=∠BAC﹣∠CAD
=(180°﹣∠B﹣∠C)﹣(90°﹣∠C)
=90°﹣∠B﹣∠C﹣90°+∠C
=∠C﹣∠B
=(∠C﹣∠B).
∵∠C﹣∠B=α,
∴∠DAE=×a=.
24.【问题背景】∠MON=90°,点A,B分别在OM,ON上运动(不与点O重合).
【问题思考】
(1)如图①所示,AE,BE分别是∠BAO和∠ABO的平分线,随着点A,B的运动,求∠AEB的值.
(2)如图②所示,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.如果∠MON=α,其余条件不变,随着点A,B的运动,求∠D的值.(用含α的代数式表示)
【解答】解:(1)∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=∠OAB,∠ABE=∠ABO,
∴∠BAE+∠ABE=(∠OAB+∠ABO)=45°,
∴∠AEB=135°;
(2)设∠BAD=x,
∵AD平分∠BAO,
∴∠BAO=2x,
∵∠AOB=α
∴∠ABN=180°﹣∠ABO=∠AOB+∠BAO=α+2x.
∵BC平分∠ABN,
∴,,
∵∠ABC=180°﹣∠ABD=∠D+∠BAD.
∴,
25.如图,AB⊥CD,垂足为O,点P、Q分别在射线OC、OA上运动(点P、Q都不与点O重合),QE是∠AQP的平分线.
(1)如图1,在点P、Q的运动过程中,若直线QE交∠DPQ的平分线于点H.
①当∠PQB=60°时,∠PHE= 45 °;
②随着点P、Q分别在OC、OA的运动,∠PHE的大小是否是定值?如果是定值,请求出∠PHE的度数;如果不是定值,请说明理由;
(2)如图2,若QE所在直线交∠QPC的平分线于点E时,将△EFG沿FG折叠,使点E落在四边形PFGQ内点E′的位置,猜测∠PFE′与∠QGE′之间的数量关系,并说明理由.
【解答】解:(1)①∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠PQB=60°,
∴∠QPO=30°,∠AQP=120°,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°,
故答案为:45;
②∠PHE 是一个定值,∠PHE=45°,理由如下:
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∴∠QPO=90°﹣∠PQO,∠AQP=180°﹣∠PQO,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°;
(2)∠PFE'+∠QGE'=90°,理由如下:
如图2所示,连接EE',
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠CPQ+∠QPO=180°,∠PQA+∠PQO=180°,
∴180°﹣∠CPQ+180°﹣∠PQA=90°,
∴∠CPQ+∠PQA=270°,
∵QE,PE分别平分∠PQA,∠CPQ,
∴,
∴,
∴∠PEQ=180°﹣∠EPQ﹣∠EQP=45°,
由折叠的性质可知∠GE'F=∠PEQ=45°,
∵∠FEE'+∠EFE'+∠EE'F=180°=∠GEE'+∠EGE'+∠EE'G,
∴∠FEG+∠FE'G+∠EFE'+∠EGE'=360°,
∴∠EFE'+∠EFE'=270°,
∵∠EFE'+∠PFE'=180°=∠EGE'+∠QGE',
∴∠PFE'+∠QGE'=360°﹣∠EFE'﹣∠EFE'=90°.
