12.3角的平分线的性质 同步练习(含答案) 2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 12.3角的平分线的性质 同步练习(含答案) 2023—2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 162.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-04 19:18:21 | ||
图片预览

文档简介
12.3角的平分线的性质
一、选择题
1.到三角形三边距离相等的点是( )
A.三边垂直平分线的交点 B.三条高所在直线的交点
C.三条角平分线的交点 D.三条中线的交点
2.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=4,AB=15,则△ABD的面积为( )
A.15 B.30 C.45 D.60
3.已知:在 中, , 平分 交BC于D,若 ,且 ,则点D到AB边的距离为( )
A.18 B.12 C.14 D.16
4.如图,OC是∠AOB的平分线,P是OC上一点,P点到OA的距离PE=2,点F是OB上任意一点,则线段PF的长的取值范围是( )
A.PF<2 B.PF>2 C.PF≥2 D.PF≤2
5.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F.若S△ABC=28,DE=4,AB=8,则AC长是( )
A.8 B.7 C.6 D.5
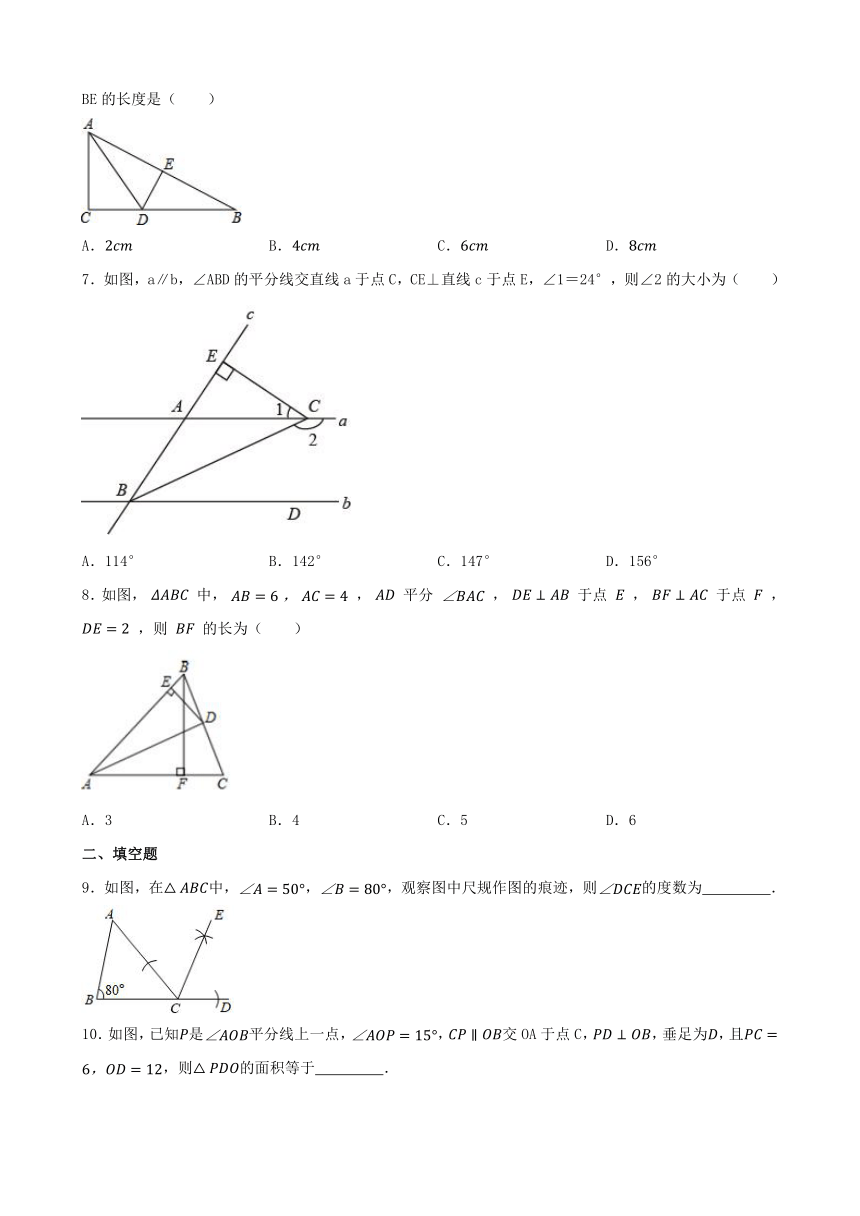
6.如如图, Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=10cm,AC=6cm,则BE的长度是( )
A. B. C. D.
7.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
8.如图, 中, , 平分 , 于点 , 于点 , ,则 的长为( )
A.3 B.4 C.5 D.6
二、填空题
9.如图,在中,,,观察图中尺规作图的痕迹,则的度数为 .
10.如图,已知是平分线上一点,,交OA于点C,,垂足为,且,则的面积等于 .
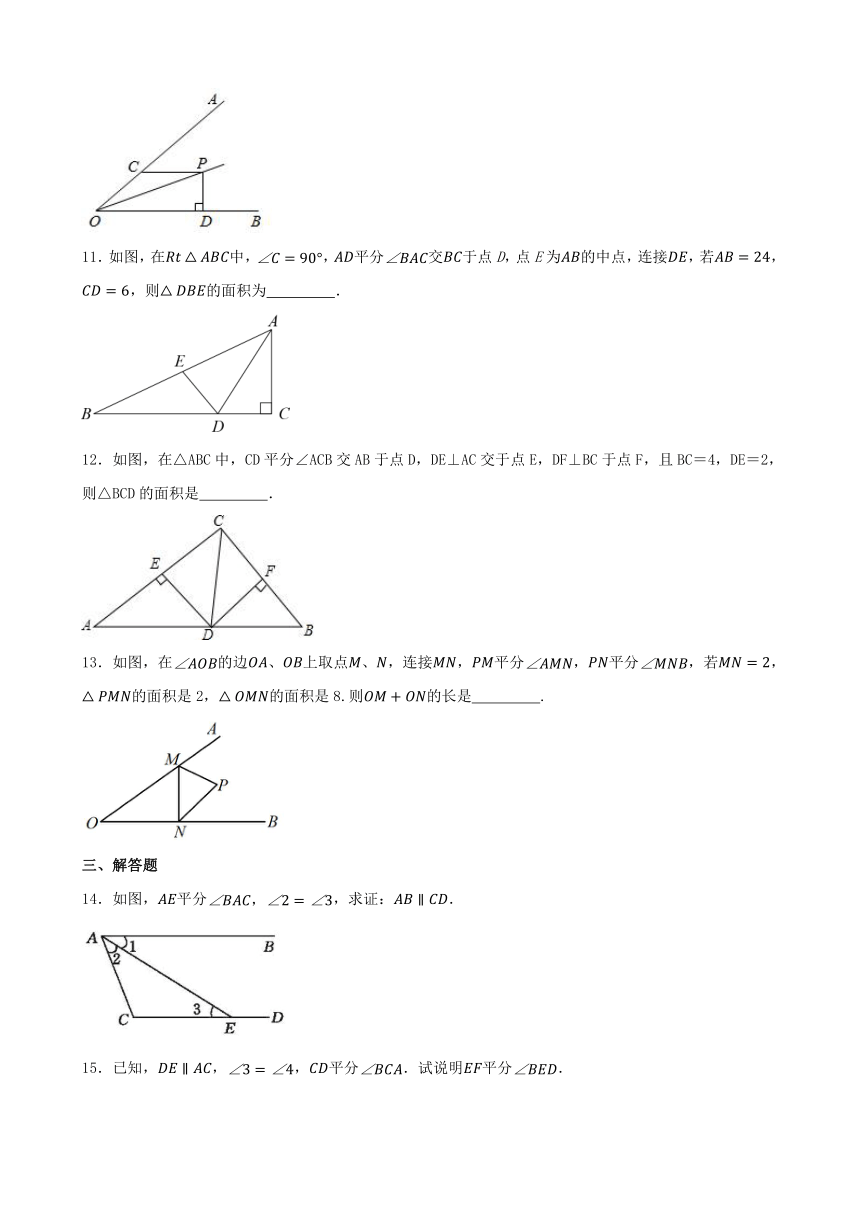
11.如图,在中,,平分交于点D,点E为的中点,连接,若,,则的面积为 .
12.如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
13.如图,在的边、上取点、,连接,平分,平分,若,的面积是2,的面积是8.则的长是 .
三、解答题
14.如图,平分,求证:.
15.已知,,,平分.试说明平分.
16.如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连接DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.
17.如图,∠B=∠C=90°,点E是BC的中点.DE平分∠ADC.
(1)求证:AE是∠DAB的平分线;
(2)已知AE=4,DE=3,求四边形ABCD的面积.
参考答案
1.C
2.B
3.B
4.C
5.C
6.B
7.C
8.C
9.65°
10.18
11.36
12.4
13.10
14.证明:平分,
.
,
,
.
15.证明:∵(已知),
∴(两直线平行,同位角相等),
即,
∵(已知),
∴(两直线平行,内错角相等);
∵(已知),
∴(等量代换),
∴(等式性质);
∵平分(已知),
∴(角平分线的定义),
∴(等量代换),
∴平分(角平分线的定义).
16.(1)证明:
过E作EH⊥AB于H,EF⊥BC于F,EG⊥AD于G,
∵AD平分∠BAC,∠BAC=120°,
∴∠BAD=∠CAD=60°,
∵∠CAH=180°﹣120°=60°,
∴AE平分∠HAD,
∴EH=EG,
∵BE平分∠ABC,EH⊥AB,EF⊥BC,
∴EH=EF,
∴EF=EG,
∴点E到DA、DC的距离相等;
(2)解:∵由(1)知:DE平分∠ADC,
∴∠EDC=∠DEB+∠DBE,
∴=∠DEB+∠ABC,
∴∠DEB=(∠CDA﹣∠ABC)=∠BAD=30°.
17.(1)证明:如图,过点E作EF⊥DA于点F,
∵∠C=90°,DE平分∠ADC,
∴CE=EF,
∵E是BC的中点,
∴BE=CE,
∴EF=EB,
又∵∠B=90°,EF⊥DA,.
∴AE平分∠DAB.
(2)解:∵EF⊥DA,∠C=90°,
∴△EFD和△ECD都为Rt△,
又∵DE平分∠ADC,
∴EC=EF,
在Rt△EFD和Rt△ECD中,
,
∴
∴
同理∠AEF=∠AEB,S△AEF=S△AEB,
∴
∵AE=4,DE=3,
∴
∴
=12
∴四边形ABCD的面积为12.
一、选择题
1.到三角形三边距离相等的点是( )
A.三边垂直平分线的交点 B.三条高所在直线的交点
C.三条角平分线的交点 D.三条中线的交点
2.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=4,AB=15,则△ABD的面积为( )
A.15 B.30 C.45 D.60
3.已知:在 中, , 平分 交BC于D,若 ,且 ,则点D到AB边的距离为( )
A.18 B.12 C.14 D.16
4.如图,OC是∠AOB的平分线,P是OC上一点,P点到OA的距离PE=2,点F是OB上任意一点,则线段PF的长的取值范围是( )
A.PF<2 B.PF>2 C.PF≥2 D.PF≤2
5.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F.若S△ABC=28,DE=4,AB=8,则AC长是( )
A.8 B.7 C.6 D.5
6.如如图, Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=10cm,AC=6cm,则BE的长度是( )
A. B. C. D.
7.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
8.如图, 中, , 平分 , 于点 , 于点 , ,则 的长为( )
A.3 B.4 C.5 D.6
二、填空题
9.如图,在中,,,观察图中尺规作图的痕迹,则的度数为 .
10.如图,已知是平分线上一点,,交OA于点C,,垂足为,且,则的面积等于 .
11.如图,在中,,平分交于点D,点E为的中点,连接,若,,则的面积为 .
12.如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
13.如图,在的边、上取点、,连接,平分,平分,若,的面积是2,的面积是8.则的长是 .
三、解答题
14.如图,平分,求证:.
15.已知,,,平分.试说明平分.
16.如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连接DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.
17.如图,∠B=∠C=90°,点E是BC的中点.DE平分∠ADC.
(1)求证:AE是∠DAB的平分线;
(2)已知AE=4,DE=3,求四边形ABCD的面积.
参考答案
1.C
2.B
3.B
4.C
5.C
6.B
7.C
8.C
9.65°
10.18
11.36
12.4
13.10
14.证明:平分,
.
,
,
.
15.证明:∵(已知),
∴(两直线平行,同位角相等),
即,
∵(已知),
∴(两直线平行,内错角相等);
∵(已知),
∴(等量代换),
∴(等式性质);
∵平分(已知),
∴(角平分线的定义),
∴(等量代换),
∴平分(角平分线的定义).
16.(1)证明:
过E作EH⊥AB于H,EF⊥BC于F,EG⊥AD于G,
∵AD平分∠BAC,∠BAC=120°,
∴∠BAD=∠CAD=60°,
∵∠CAH=180°﹣120°=60°,
∴AE平分∠HAD,
∴EH=EG,
∵BE平分∠ABC,EH⊥AB,EF⊥BC,
∴EH=EF,
∴EF=EG,
∴点E到DA、DC的距离相等;
(2)解:∵由(1)知:DE平分∠ADC,
∴∠EDC=∠DEB+∠DBE,
∴=∠DEB+∠ABC,
∴∠DEB=(∠CDA﹣∠ABC)=∠BAD=30°.
17.(1)证明:如图,过点E作EF⊥DA于点F,
∵∠C=90°,DE平分∠ADC,
∴CE=EF,
∵E是BC的中点,
∴BE=CE,
∴EF=EB,
又∵∠B=90°,EF⊥DA,.
∴AE平分∠DAB.
(2)解:∵EF⊥DA,∠C=90°,
∴△EFD和△ECD都为Rt△,
又∵DE平分∠ADC,
∴EC=EF,
在Rt△EFD和Rt△ECD中,
,
∴
∴
同理∠AEF=∠AEB,S△AEF=S△AEB,
∴
∵AE=4,DE=3,
∴
∴
=12
∴四边形ABCD的面积为12.
