第十一章 三角形 单元练习(含答案) 2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 第十一章 三角形 单元练习(含答案) 2023—2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 168.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-04 21:44:04 | ||
图片预览

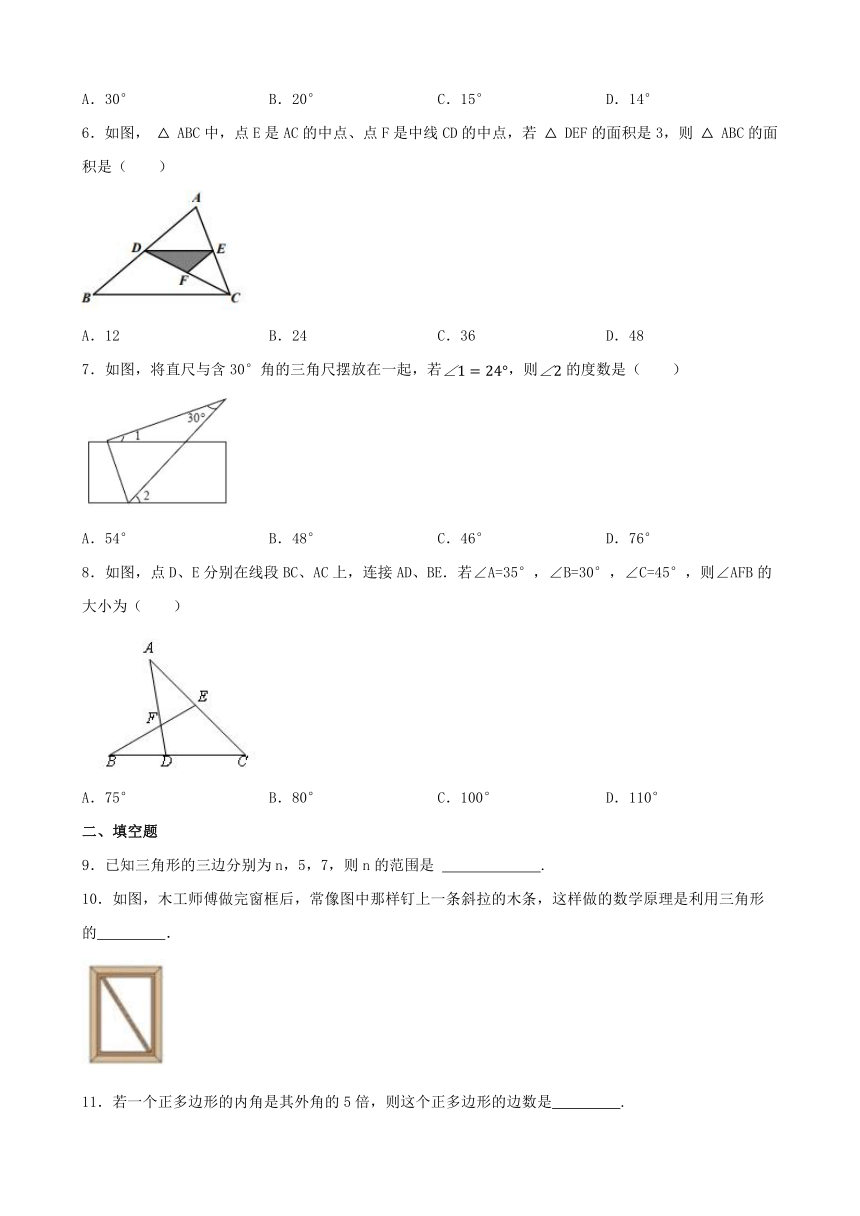
文档简介
第十一章 三角形
一、选择题
1.下列长度的三条线段,能组成三角形的是( )
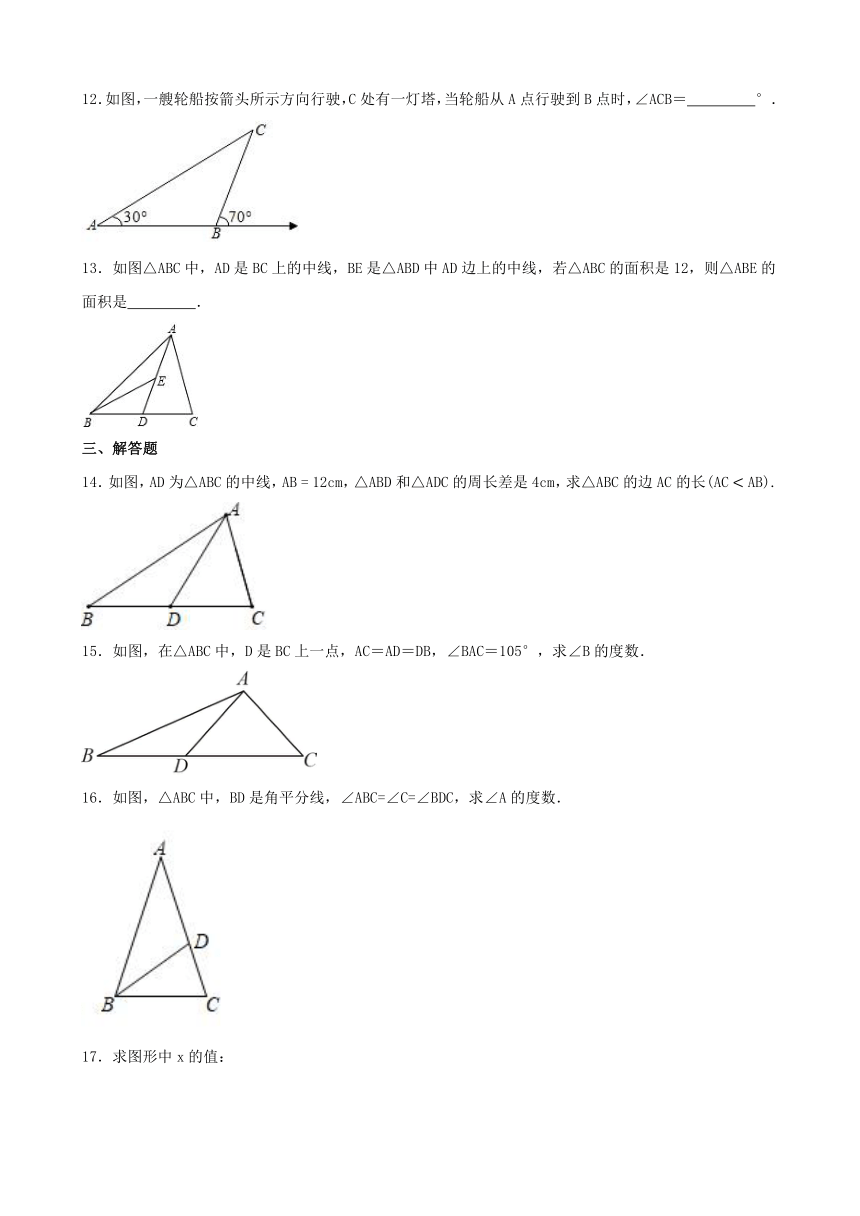
A.,, B.,,
C.,, D.,,
2.在下列图形中,正确画出△ABC的边BC上的高的是( )
A. B.
C. D.
3.如图,人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.三角形具有稳定性 B.垂线段最短
C.两点之间,线段最短 D.两直线平行,内错角相等
4.如果过一个多边形的一个顶点的对角线有5条,则该多边形是( )
A.九边形 B.八边形 C.七边形 D.六边形
5.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
A.30° B.20° C.15° D.14°
6.如图, ABC中,点E是AC的中点、点F是中线CD的中点,若 DEF的面积是3,则 ABC的面积是( )
A.12 B.24 C.36 D.48
7.如图,将直尺与含30°角的三角尺摆放在一起,若,则的度数是( )
A.54° B.48° C.46° D.76°
8.如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=30°,∠C=45°,则∠AFB的大小为( )
A.75° B.80° C.100° D.110°
二、填空题
9.已知三角形的三边分别为n,5,7,则n的范围是 .
10.如图,木工师傅做完窗框后,常像图中那样钉上一条斜拉的木条,这样做的数学原理是利用三角形的 .
11.若一个正多边形的内角是其外角的5倍,则这个正多边形的边数是 .
12.如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,当轮船从A点行驶到B点时,∠ACB= °.
13.如图△ABC中,AD是BC上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是12,则△ABE的面积是 .
三、解答题
14.如图,AD为△ABC的中线,AB = 12cm,△ABD和△ADC的周长差是4cm,求△ABC的边AC的长(AC AB).
15.如图,在△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,求∠B的度数.
16.如图,△ABC中,BD是角平分线,∠ABC=∠C=∠BDC,求∠A的度数.
17.求图形中x的值:
18.如图所示,在中,平分交于点E,交于点D,,,求的度数.
参考答案
1.D
2.C
3.A
4.B
5.C
6.B
7.A
8.D
9.2<n<12
10.稳定性
11.12
12.40
13.3
14.解:∵AD为△ABC的中线,
∴BD = CD,
∵△ABD和△ADC的周长差是4cm,
∴AB + AD + BD – (AC + AD + CD) = AB + AD + BD – AC – AD – BD = AB – AC = 4cm,
∵AB = 12cm,
∴AC = AB – 4cm = 8cm.
15.解:∵,
∴,.
设,
∴.
∵,
∴,
在中,
∵,
∴,
∴,
∴.
16.解:设∠DBC=x,
∵BD是角平分线,
∴∠ABD=∠DBC,
∴∠ABD=∠DBC=x,则∠ABC=∠C=∠BDC=2x,
∵∠BDC=∠A+∠ABD,即2x=∠A+x,
∴∠A=x,
∴x+2x+2x=180°,
解得,x=36°,
∴∠A的度数为36°.
17.∵∠A+∠B+∠C+∠D+∠E=180°×(5﹣2),
∴x+(x+20°)+70°+x+(x﹣10°)=540°,
4x=460°,
x=115°.
18.解:∵,
∴
∵平分,,
∴,
∵,
∴,
∴,
∴.
一、选择题
1.下列长度的三条线段,能组成三角形的是( )
A.,, B.,,
C.,, D.,,
2.在下列图形中,正确画出△ABC的边BC上的高的是( )
A. B.
C. D.
3.如图,人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.三角形具有稳定性 B.垂线段最短
C.两点之间,线段最短 D.两直线平行,内错角相等
4.如果过一个多边形的一个顶点的对角线有5条,则该多边形是( )
A.九边形 B.八边形 C.七边形 D.六边形
5.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
A.30° B.20° C.15° D.14°
6.如图, ABC中,点E是AC的中点、点F是中线CD的中点,若 DEF的面积是3,则 ABC的面积是( )
A.12 B.24 C.36 D.48
7.如图,将直尺与含30°角的三角尺摆放在一起,若,则的度数是( )
A.54° B.48° C.46° D.76°
8.如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=30°,∠C=45°,则∠AFB的大小为( )
A.75° B.80° C.100° D.110°
二、填空题
9.已知三角形的三边分别为n,5,7,则n的范围是 .
10.如图,木工师傅做完窗框后,常像图中那样钉上一条斜拉的木条,这样做的数学原理是利用三角形的 .
11.若一个正多边形的内角是其外角的5倍,则这个正多边形的边数是 .
12.如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,当轮船从A点行驶到B点时,∠ACB= °.
13.如图△ABC中,AD是BC上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是12,则△ABE的面积是 .
三、解答题
14.如图,AD为△ABC的中线,AB = 12cm,△ABD和△ADC的周长差是4cm,求△ABC的边AC的长(AC AB).
15.如图,在△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,求∠B的度数.
16.如图,△ABC中,BD是角平分线,∠ABC=∠C=∠BDC,求∠A的度数.
17.求图形中x的值:
18.如图所示,在中,平分交于点E,交于点D,,,求的度数.
参考答案
1.D
2.C
3.A
4.B
5.C
6.B
7.A
8.D
9.2<n<12
10.稳定性
11.12
12.40
13.3
14.解:∵AD为△ABC的中线,
∴BD = CD,
∵△ABD和△ADC的周长差是4cm,
∴AB + AD + BD – (AC + AD + CD) = AB + AD + BD – AC – AD – BD = AB – AC = 4cm,
∵AB = 12cm,
∴AC = AB – 4cm = 8cm.
15.解:∵,
∴,.
设,
∴.
∵,
∴,
在中,
∵,
∴,
∴,
∴.
16.解:设∠DBC=x,
∵BD是角平分线,
∴∠ABD=∠DBC,
∴∠ABD=∠DBC=x,则∠ABC=∠C=∠BDC=2x,
∵∠BDC=∠A+∠ABD,即2x=∠A+x,
∴∠A=x,
∴x+2x+2x=180°,
解得,x=36°,
∴∠A的度数为36°.
17.∵∠A+∠B+∠C+∠D+∠E=180°×(5﹣2),
∴x+(x+20°)+70°+x+(x﹣10°)=540°,
4x=460°,
x=115°.
18.解:∵,
∴
∵平分,,
∴,
∵,
∴,
∴,
∴.
