人教版六年级数学下册《圆锥的体积》课件(共24张PPT)
文档属性
| 名称 | 人教版六年级数学下册《圆锥的体积》课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-04 08:51:13 | ||
图片预览






文档简介
(共24张PPT)
圆锥的体积
第三单元 圆柱与圆锥
圆锥的体积
创设情境
上面两种冰淇淋的价格都是5元一个,请大家帮老师参考一下买哪一种最合算?
你们喜欢吃冰淇淋吗?
创设情境
冰淇淋包装盒是什么形状呢?
冰淇淋包装盒是圆锥。
知识回顾
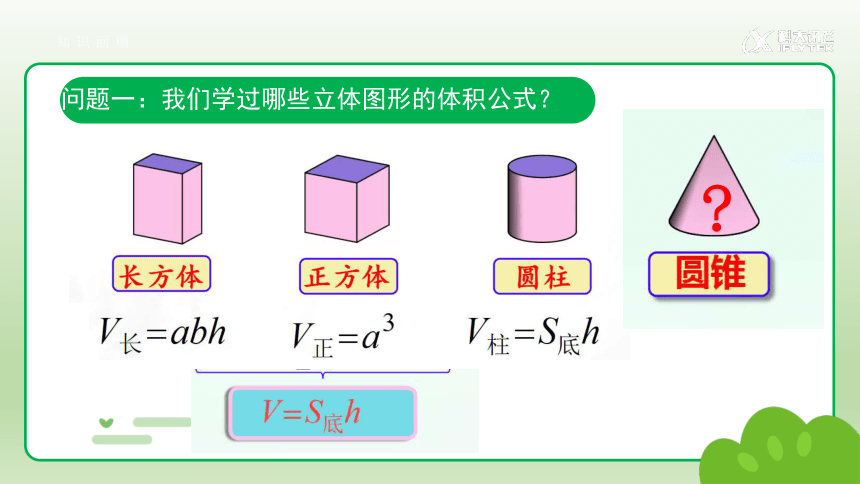
问题一:我们学过哪些立体图形的体积公式?
探究新知
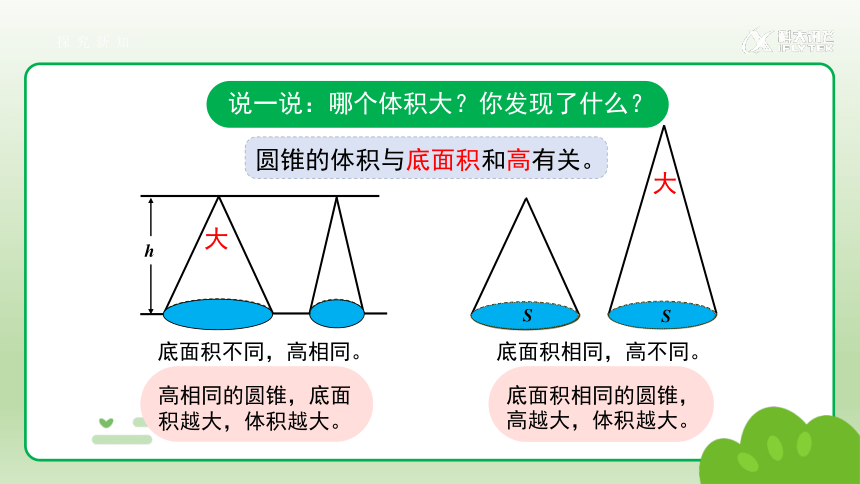
说一说:哪个体积大?你发现了什么?
底面积相同的圆锥,高越大,体积越大。
大
大
底面积相同,高不同。
底面积不同,高相同。
圆锥的体积与底面积和高有关。
高相同的圆锥,底面积越大,体积越大。
h
S
S
探究新知
问题一:我们学过哪些立体图形的体积公式
问题二:圆锥的体积可能和哪个立体图形的体积有关呢?为什么?
圆柱的底面是圆,圆锥的底面也是圆。
探究新知
问题三:圆锥的体积可能与等底等高的圆柱有什么关系?
●
●
圆锥的体积应该与同它等高等底的圆柱体积有关。
圆锥的体积可能是它等高等底的圆柱体积的。
这些猜想都正确吗?
探究新知
小组合作,验证猜想
探索圆锥体积和圆柱体积之间的关系
实验要求:
1.全体组员起立,轻推凳子,前后四人为一小组,小组成员分工合作:两人操作,一人记录,一人汇报。
2.实验前先观察你拿到的圆柱和圆锥的相同点和不同点。
3.根据记录单的要求做实验,操作时尽量不要将水或者沙子撒出来,装水时要装满,减小误差。
4.实验完成后,小组讨论结果,认真填写记录单,并整理好实验器具和卫生,端正坐姿。
方法一:将圆锥形容器装满沙子或水,倒入圆柱形容器里,倒满为止。倒几次?
方法二:将圆柱形容器装满沙子或水,再倒入圆锥形的容器里,倒完为止。倒几次?
(3)通过实验你有什么发现?由此可以得出什么结论?
输入标题
1次
2次
3次
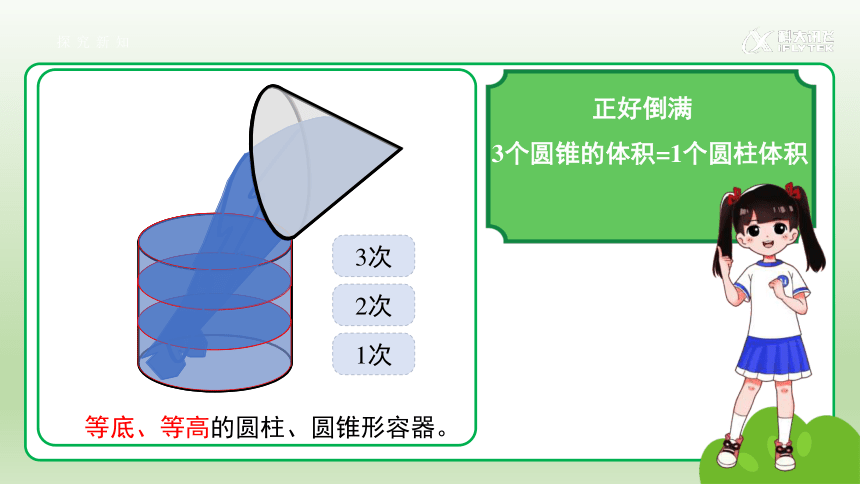
正好倒满
3个圆锥的体积=1个圆柱体积
等底、等高的圆柱、圆锥形容器。
探究新知
等底等高
圆柱的体积等于圆锥体积的3倍
圆锥的体积等于圆柱体积的
通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
归纳小结
探究新知
圆锥体积计算公式推导
讨论:已知以下信息,怎么求圆锥的体积
底面半径和高
V圆锥= πr2h
底面直径和高
V圆锥= π h
V圆锥= π h
底面周长和高
回顾课始问题
你能解决老师的这个问题吗?
S=30cm
h=9cm
S=50cm
h=6cm
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重多少吨?
4 m
1.5 m
求沙子的体积就是求圆锥的体积。
底面直径
高
把直径转化为半径,再求出底面积。
先算什么?再算什么?
沙子的质量=圆锥的体积×沙子每立方米的质量
探究新知
输入标题
沙堆底面积:3.14 ×(4÷2)2=12.56(m2)
沙堆重:6.28×1.5=9.42(t)
答:这堆沙子的体积大约是6.28 m3,大约重9.42 t。
×12.56×1.5=6.28(m3)
沙堆的体积:
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重多少吨?
4 m
1.5 m
底面直径
高
沙子的质量=圆锥的体积×沙子每立方米的质量
探究新知
输入标题
=
圆锥的体积等于与它等底等高圆柱体积的。
归 纳
实验
等量关系
结论
字母表示
探究新知
1.(1)一个圆柱的体积是75.36m3,与它等底、等高的
圆锥的体积是( )m3。
(2)一个圆锥的体积是141.3m3,与它等底、等高的
圆柱的体积是( )m3。
25.12
423.9
(教材P34 练习六T3)
输入标题
2.判断对错,对的画“√”,错的画“×”。
(1)圆锥的体积等于圆柱体积的。 ( )
(2)圆柱的体积大于与它等底等高的圆锥的体积。( )
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。 ( )
(4)一个圆柱形木料,将它加工成最大的圆锥,削去部分的体积和圆锥的体积比是2:1 ( )
×
√
×
巩固练习
圆柱和圆柱不一定是等底等高的
不一定,圆柱和圆锥的底面积不一定是相等的
√
输入标题
3.一个圆锥的底面周长是31.4 cm,高是9 cm。它的体积是多少?
×3.14×(31.4÷3.14÷2)2×9=235.5(cm3)
答:它的体积是235.5 cm3。
V = Sh
V=πh
巩固练习
输入标题
4.相信你能行
(1)把一个圆柱形零件削成一个最大的圆锥形零件,体积减少16.8立方分米,原来零件的体积是( )立方分米。
(2)等底等高的一个圆锥体和一个圆柱体组成组合体,组合体的体积是48立方分米,圆锥体积是( )立方分米,圆柱体体积是( )立方分米。
巩固练习
输入标题
5.一个用钢铸造成的圆锥形铅锤,底面直径是4 cm,高6 cm。每立方厘米钢大约重7.9 g。这个铅锤重多少克?(得数保留整数。)
答:这个铅锤重198克。
质量=铅锤的体积×每立方厘米钢的质量
铅锤底面积:
3.14×(4÷2)2=3.14×4=12.56(cm2)
铅锤的体积:
×12.56×6≈25.09(cm3)
25.09×7.9≈198(g)
铅锤的质量:
巩固练习
今天的学习你有什么收获?
课堂小结
圆锥体积等于与它等底等高圆柱体积的
=
实验
结论
字母表示
课后活动
观察生活中的圆锥形,你能计算它们的体积吗,和小伙伴们一起交流一下吧!
输入标题
拓展延伸
如图,把一个体积是73 dm 的圆柱形木块,削成两个顶点相连的完全相同的圆锥形木块,形成“沙漏”状,那么每个圆锥的体积是多少立方分米?
h
72×÷2
=24÷2
=12(dm3)
h
答:每个圆锥的体积是12 dm 。
小圆锥和圆柱的体积有什么关系?
高有什么关系?底面积有什么关系?
圆锥的体积
第三单元 圆柱与圆锥
圆锥的体积
创设情境
上面两种冰淇淋的价格都是5元一个,请大家帮老师参考一下买哪一种最合算?
你们喜欢吃冰淇淋吗?
创设情境
冰淇淋包装盒是什么形状呢?
冰淇淋包装盒是圆锥。
知识回顾
问题一:我们学过哪些立体图形的体积公式?
探究新知
说一说:哪个体积大?你发现了什么?
底面积相同的圆锥,高越大,体积越大。
大
大
底面积相同,高不同。
底面积不同,高相同。
圆锥的体积与底面积和高有关。
高相同的圆锥,底面积越大,体积越大。
h
S
S
探究新知
问题一:我们学过哪些立体图形的体积公式
问题二:圆锥的体积可能和哪个立体图形的体积有关呢?为什么?
圆柱的底面是圆,圆锥的底面也是圆。
探究新知
问题三:圆锥的体积可能与等底等高的圆柱有什么关系?
●
●
圆锥的体积应该与同它等高等底的圆柱体积有关。
圆锥的体积可能是它等高等底的圆柱体积的。
这些猜想都正确吗?
探究新知
小组合作,验证猜想
探索圆锥体积和圆柱体积之间的关系
实验要求:
1.全体组员起立,轻推凳子,前后四人为一小组,小组成员分工合作:两人操作,一人记录,一人汇报。
2.实验前先观察你拿到的圆柱和圆锥的相同点和不同点。
3.根据记录单的要求做实验,操作时尽量不要将水或者沙子撒出来,装水时要装满,减小误差。
4.实验完成后,小组讨论结果,认真填写记录单,并整理好实验器具和卫生,端正坐姿。
方法一:将圆锥形容器装满沙子或水,倒入圆柱形容器里,倒满为止。倒几次?
方法二:将圆柱形容器装满沙子或水,再倒入圆锥形的容器里,倒完为止。倒几次?
(3)通过实验你有什么发现?由此可以得出什么结论?
输入标题
1次
2次
3次
正好倒满
3个圆锥的体积=1个圆柱体积
等底、等高的圆柱、圆锥形容器。
探究新知
等底等高
圆柱的体积等于圆锥体积的3倍
圆锥的体积等于圆柱体积的
通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
归纳小结
探究新知
圆锥体积计算公式推导
讨论:已知以下信息,怎么求圆锥的体积
底面半径和高
V圆锥= πr2h
底面直径和高
V圆锥= π h
V圆锥= π h
底面周长和高
回顾课始问题
你能解决老师的这个问题吗?
S=30cm
h=9cm
S=50cm
h=6cm
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重多少吨?
4 m
1.5 m
求沙子的体积就是求圆锥的体积。
底面直径
高
把直径转化为半径,再求出底面积。
先算什么?再算什么?
沙子的质量=圆锥的体积×沙子每立方米的质量
探究新知
输入标题
沙堆底面积:3.14 ×(4÷2)2=12.56(m2)
沙堆重:6.28×1.5=9.42(t)
答:这堆沙子的体积大约是6.28 m3,大约重9.42 t。
×12.56×1.5=6.28(m3)
沙堆的体积:
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重多少吨?
4 m
1.5 m
底面直径
高
沙子的质量=圆锥的体积×沙子每立方米的质量
探究新知
输入标题
=
圆锥的体积等于与它等底等高圆柱体积的。
归 纳
实验
等量关系
结论
字母表示
探究新知
1.(1)一个圆柱的体积是75.36m3,与它等底、等高的
圆锥的体积是( )m3。
(2)一个圆锥的体积是141.3m3,与它等底、等高的
圆柱的体积是( )m3。
25.12
423.9
(教材P34 练习六T3)
输入标题
2.判断对错,对的画“√”,错的画“×”。
(1)圆锥的体积等于圆柱体积的。 ( )
(2)圆柱的体积大于与它等底等高的圆锥的体积。( )
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。 ( )
(4)一个圆柱形木料,将它加工成最大的圆锥,削去部分的体积和圆锥的体积比是2:1 ( )
×
√
×
巩固练习
圆柱和圆柱不一定是等底等高的
不一定,圆柱和圆锥的底面积不一定是相等的
√
输入标题
3.一个圆锥的底面周长是31.4 cm,高是9 cm。它的体积是多少?
×3.14×(31.4÷3.14÷2)2×9=235.5(cm3)
答:它的体积是235.5 cm3。
V = Sh
V=πh
巩固练习
输入标题
4.相信你能行
(1)把一个圆柱形零件削成一个最大的圆锥形零件,体积减少16.8立方分米,原来零件的体积是( )立方分米。
(2)等底等高的一个圆锥体和一个圆柱体组成组合体,组合体的体积是48立方分米,圆锥体积是( )立方分米,圆柱体体积是( )立方分米。
巩固练习
输入标题
5.一个用钢铸造成的圆锥形铅锤,底面直径是4 cm,高6 cm。每立方厘米钢大约重7.9 g。这个铅锤重多少克?(得数保留整数。)
答:这个铅锤重198克。
质量=铅锤的体积×每立方厘米钢的质量
铅锤底面积:
3.14×(4÷2)2=3.14×4=12.56(cm2)
铅锤的体积:
×12.56×6≈25.09(cm3)
25.09×7.9≈198(g)
铅锤的质量:
巩固练习
今天的学习你有什么收获?
课堂小结
圆锥体积等于与它等底等高圆柱体积的
=
实验
结论
字母表示
课后活动
观察生活中的圆锥形,你能计算它们的体积吗,和小伙伴们一起交流一下吧!
输入标题
拓展延伸
如图,把一个体积是73 dm 的圆柱形木块,削成两个顶点相连的完全相同的圆锥形木块,形成“沙漏”状,那么每个圆锥的体积是多少立方分米?
h
72×÷2
=24÷2
=12(dm3)
h
答:每个圆锥的体积是12 dm 。
小圆锥和圆柱的体积有什么关系?
高有什么关系?底面积有什么关系?
