4.3 牛顿第二定律(课件)(共22张PPT) 高一物理人教版(2019)必修第一册
文档属性
| 名称 | 4.3 牛顿第二定律(课件)(共22张PPT) 高一物理人教版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-05 21:39:02 | ||
图片预览





文档简介
(共22张PPT)
第4章 运动和力的关系
第3节 牛顿第二定律
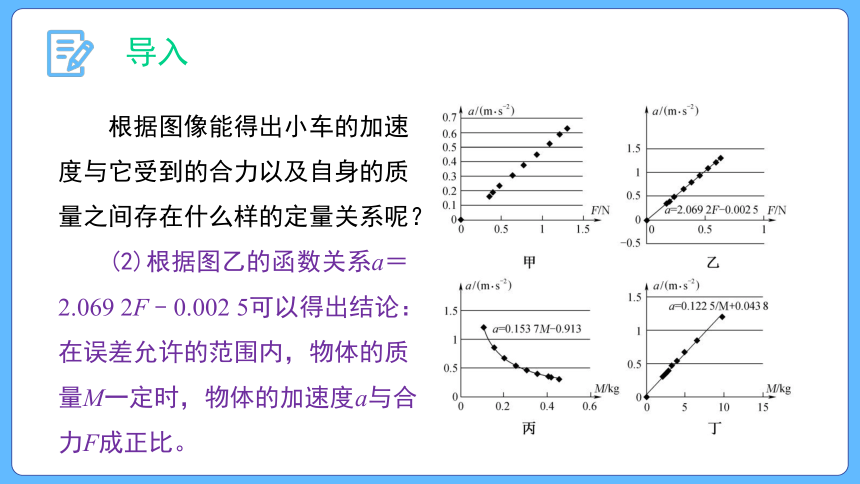
根据图像能得出小车的加速
度与它受到的合力以及自身的质
量之间存在什么样的定量关系呢?
(1)根据图甲可以得到结论:
物体的质量M一定时,物体的加
速度a与合力F呈线性关系。
导入
根据图像能得出小车的加速
度与它受到的合力以及自身的质
量之间存在什么样的定量关系呢?
(2)根据图乙的函数关系a=
2.069 2F﹣0.002 5可以得出结论:
在误差允许的范围内,物体的质
量M一定时,物体的加速度a与合
力F成正比。
导入
根据图像能得出小车的加速
度与它受到的合力以及自身的质
量之间存在什么样的定量关系呢?
(3)从图丙的解析式a=
0.153 7M﹣0.913可得出结论:合
力F一定时,加速度a与质量M成
反比。但如果没有解析式是很难
判断a与M的具体关系的。
导入
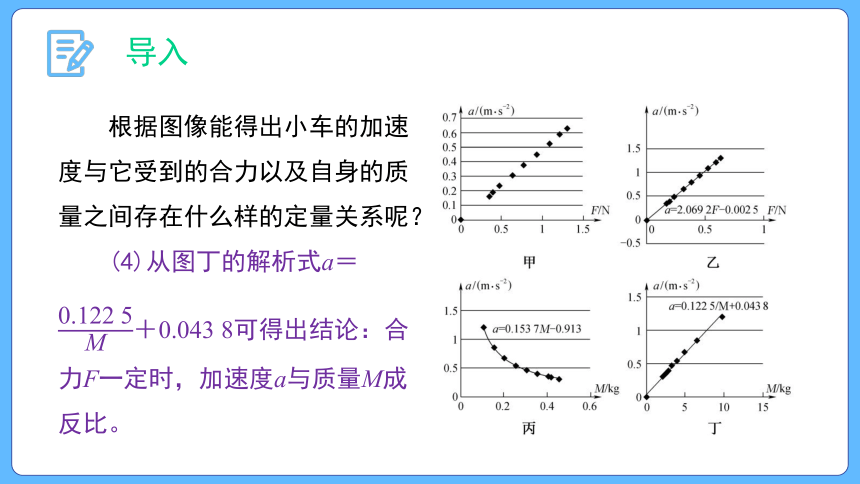
根据图像能得出小车的加速
度与它受到的合力以及自身的质
量之间存在什么样的定量关系呢?
(4)从图丁的解析式a=
+0.043 8可得出结论:合
力F一定时,加速度a与质量M成
反比。
导入
从前面出示的图像我们能看到,小车的加速度a与其受到的合力F并不是真的成正比,与小车的质量M也并不是真的成反比,因为这组同学得到的a-F、a-图像的截距都不为0。
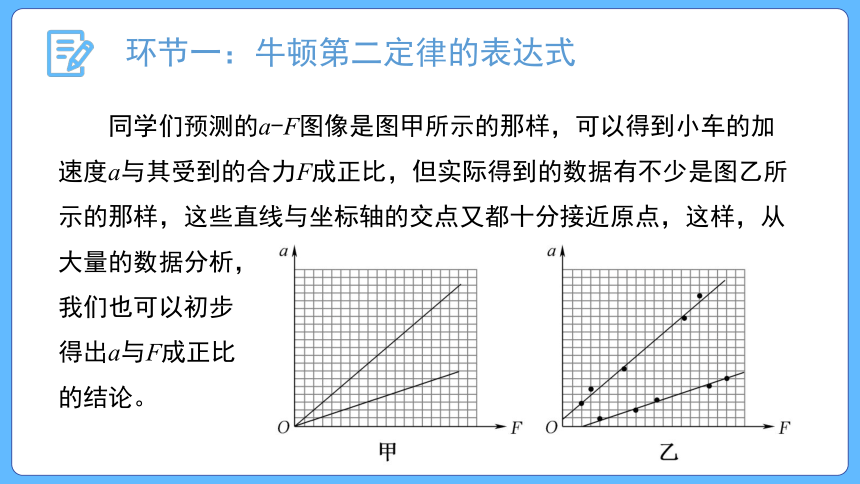
环节一:牛顿第二定律的表达式
同学们预测的a-F图像是图甲所示的那样,可以得到小车的加速度a与其受到的合力F成正比,但实际得到的数据有不少是图乙所示的那样,这些直线与坐标轴的交点又都十分接近原点,这样,从大量的数据分析,
我们也可以初步
得出a与F成正比
的结论。
环节一:牛顿第二定律的表达式
同样,各小组几乎也都得到了小车运动的加速度a与它的质量m成反比的结论。但这个结论是否具有普遍性呢?或者说,对其他任何物体,都有这样的结论吗?我们应该怎么做才能验证这一猜想呢?
将实验结论应用于更多事例来进行检验,用实验事实以及实际现象去验证。
经过大量的实验和观察到的事实都可以得出与上节实验结论相同的结论,由此可以总结出一般性的规律。
环节一:牛顿第二定律的表达式
环节一:牛顿第二定律的表达式
思路一
实验结论:m一定,a∝F;F一定,a∝(说明:此处m指研究对象的质量)。由此可以得出a∝,可以写成等式F=kma,式中k是比例系数。
这就是牛顿第二定律,其内容是:物体加速度的大小跟它受到的作用力成正比,跟它的质量成反比,加速度的方向跟作用力的方向相同。
环节一:牛顿第二定律的表达式
思路二
由实验可以得到结论:m一定,a∝F;F一定,a∝。根据这些结论可以得出什么样的关系式呢?
可以直接写出关系式a∝,再进行变形写出F=kma。
我们可以从两个实验结论分别写出a=k1F和a=k2,能直接写成a=k吗?
在研究中,先让物体从状态1到一个中间状态,再让物体从中
间状态到状态2。每个状态对应的物理量的大小,以及状态变化过程中保持的不变量如图所示。请根据实验结论写出状态1与中间状态的关系式和中间状态与状态2的关系式。
环节一:牛顿第二定律的表达式
(1)由质量一定时加速度与合力成正比的结论可得:=。
(2)由合力一定时加速度与质量成反比的结论可得:=。
环节一:牛顿第二定律的表达式
你能否将=和=写成一个关系式?
a0相同,所以可得:a0==→=。
是否可以从上式拓展到更一般的关系式呢?
====…==k。
由此可得:F=kma。
环节一:牛顿第二定律的表达式
牛顿第二定律:物体加速度的大小跟它受到的作用力成正比,跟它的质量成反比,加速度的方向跟作用力的方向相同。
表达式:F=kma。
环节一:牛顿第二定律的表达式
力的单位是牛顿,你知道1 N是怎样定义的吗?由F=ma能定义力的单位吗?
当k=1时,质量为1 kg的物体在某力作用下获得1 m/s2的加速度,则这个力为F=ma=1 kg·m/s2。
这个力就是一个单位的力,力的单位就是kg·m/s2 。为了纪念牛顿,把力的单位称作“牛顿”。即1 N= 1 kg·m/s2 。
在质量的单位取千克(kg),加速度的单位取米每二次方秒(m/s2),力的单位取牛顿(N)时,牛顿第二定律写为F=ma。
环节一:牛顿第二定律的表达式
物体通常会同时受到多个力的作用,你可以怎么确定物体的加速度呢?
先求合力,再求加速度。
还可以怎样求加速度呢?物体的加速度是合力作用的结果,是不是每个力都有贡献,或者每个力都能产生一个加速度呢?
可以先求每个力的加速度,再求合加速度。
环节一:牛顿第二定律的表达式
比较a=与a=,这两个关系式有什么区别?
(1)a=是定义式,a与Δv、Δt无关,表示时间Δt内的平均加速度,Δt→0时表示瞬时加速度,加速度的方向与时间Δt内的速度变化量的方向相同。
(2)a=是决定式,a由F、m决定,具有瞬时性(即a与F同时产生,同时消失),加速度的方向与F的方向相同。
(3)由a=可知,F相同时,a越大说明运动状态越易改变,物体的惯性越小。
环节一:牛顿第二定律的表达式
例1 在平直路面上,质量为1 100 kg的汽车在进行研发测试,当速度达到100 km/h时取消动力,汽车经过70 s停了下来。汽车受到的阻力是多大 汽车重新起步加速时,牵引力为2 000 N,产生的加速度是多少 假定试车过程中汽车受到的阻力不变。
初速度为v0=100 km/h=27.8 m/s,末速度为0,滑行时间为t=70 s。
根据加速度的定义式得a==﹣0.397 m/s2,
根据牛顿第二定律得汽车受到的阻力为F阻=ma=﹣437 N。
重新起步后,汽车所受的合力为F合=F牵+F阻=1 563 N。
由牛顿第二定律可以得到汽车的加速度为a==1.42 m/s2,
重新起步产生的加速度的方向与运动方向相同。
环节二:牛顿第二定律的应用
例2 某同学在列车车厢的顶部用细线悬挂一个小球,
在列车以某一加速度渐渐启动的过程中,细线就会偏过一
定角度并相对车厢保持静止,通过测定偏角的大小就能确
定列车的加速度。在某次测定中,悬线与竖直方向的夹角
为θ,求列车的加速度。
设小球的质量为m,小球在竖直平面内受到重力mg、绳的拉力FT,在这两个力的作用下,小球产生水平方向的加速度a。这表明,FT与mg的合力方向水平向右。
根据牛顿第二定律得mgtan θ=ma,
解得a==gtan θ。
加速度的方向水平向右。
环节二:牛顿第二定律的应用
课堂练习
B
课堂练习
A
谢谢!
第4章 运动和力的关系
第3节 牛顿第二定律
根据图像能得出小车的加速
度与它受到的合力以及自身的质
量之间存在什么样的定量关系呢?
(1)根据图甲可以得到结论:
物体的质量M一定时,物体的加
速度a与合力F呈线性关系。
导入
根据图像能得出小车的加速
度与它受到的合力以及自身的质
量之间存在什么样的定量关系呢?
(2)根据图乙的函数关系a=
2.069 2F﹣0.002 5可以得出结论:
在误差允许的范围内,物体的质
量M一定时,物体的加速度a与合
力F成正比。
导入
根据图像能得出小车的加速
度与它受到的合力以及自身的质
量之间存在什么样的定量关系呢?
(3)从图丙的解析式a=
0.153 7M﹣0.913可得出结论:合
力F一定时,加速度a与质量M成
反比。但如果没有解析式是很难
判断a与M的具体关系的。
导入
根据图像能得出小车的加速
度与它受到的合力以及自身的质
量之间存在什么样的定量关系呢?
(4)从图丁的解析式a=
+0.043 8可得出结论:合
力F一定时,加速度a与质量M成
反比。
导入
从前面出示的图像我们能看到,小车的加速度a与其受到的合力F并不是真的成正比,与小车的质量M也并不是真的成反比,因为这组同学得到的a-F、a-图像的截距都不为0。
环节一:牛顿第二定律的表达式
同学们预测的a-F图像是图甲所示的那样,可以得到小车的加速度a与其受到的合力F成正比,但实际得到的数据有不少是图乙所示的那样,这些直线与坐标轴的交点又都十分接近原点,这样,从大量的数据分析,
我们也可以初步
得出a与F成正比
的结论。
环节一:牛顿第二定律的表达式
同样,各小组几乎也都得到了小车运动的加速度a与它的质量m成反比的结论。但这个结论是否具有普遍性呢?或者说,对其他任何物体,都有这样的结论吗?我们应该怎么做才能验证这一猜想呢?
将实验结论应用于更多事例来进行检验,用实验事实以及实际现象去验证。
经过大量的实验和观察到的事实都可以得出与上节实验结论相同的结论,由此可以总结出一般性的规律。
环节一:牛顿第二定律的表达式
环节一:牛顿第二定律的表达式
思路一
实验结论:m一定,a∝F;F一定,a∝(说明:此处m指研究对象的质量)。由此可以得出a∝,可以写成等式F=kma,式中k是比例系数。
这就是牛顿第二定律,其内容是:物体加速度的大小跟它受到的作用力成正比,跟它的质量成反比,加速度的方向跟作用力的方向相同。
环节一:牛顿第二定律的表达式
思路二
由实验可以得到结论:m一定,a∝F;F一定,a∝。根据这些结论可以得出什么样的关系式呢?
可以直接写出关系式a∝,再进行变形写出F=kma。
我们可以从两个实验结论分别写出a=k1F和a=k2,能直接写成a=k吗?
在研究中,先让物体从状态1到一个中间状态,再让物体从中
间状态到状态2。每个状态对应的物理量的大小,以及状态变化过程中保持的不变量如图所示。请根据实验结论写出状态1与中间状态的关系式和中间状态与状态2的关系式。
环节一:牛顿第二定律的表达式
(1)由质量一定时加速度与合力成正比的结论可得:=。
(2)由合力一定时加速度与质量成反比的结论可得:=。
环节一:牛顿第二定律的表达式
你能否将=和=写成一个关系式?
a0相同,所以可得:a0==→=。
是否可以从上式拓展到更一般的关系式呢?
====…==k。
由此可得:F=kma。
环节一:牛顿第二定律的表达式
牛顿第二定律:物体加速度的大小跟它受到的作用力成正比,跟它的质量成反比,加速度的方向跟作用力的方向相同。
表达式:F=kma。
环节一:牛顿第二定律的表达式
力的单位是牛顿,你知道1 N是怎样定义的吗?由F=ma能定义力的单位吗?
当k=1时,质量为1 kg的物体在某力作用下获得1 m/s2的加速度,则这个力为F=ma=1 kg·m/s2。
这个力就是一个单位的力,力的单位就是kg·m/s2 。为了纪念牛顿,把力的单位称作“牛顿”。即1 N= 1 kg·m/s2 。
在质量的单位取千克(kg),加速度的单位取米每二次方秒(m/s2),力的单位取牛顿(N)时,牛顿第二定律写为F=ma。
环节一:牛顿第二定律的表达式
物体通常会同时受到多个力的作用,你可以怎么确定物体的加速度呢?
先求合力,再求加速度。
还可以怎样求加速度呢?物体的加速度是合力作用的结果,是不是每个力都有贡献,或者每个力都能产生一个加速度呢?
可以先求每个力的加速度,再求合加速度。
环节一:牛顿第二定律的表达式
比较a=与a=,这两个关系式有什么区别?
(1)a=是定义式,a与Δv、Δt无关,表示时间Δt内的平均加速度,Δt→0时表示瞬时加速度,加速度的方向与时间Δt内的速度变化量的方向相同。
(2)a=是决定式,a由F、m决定,具有瞬时性(即a与F同时产生,同时消失),加速度的方向与F的方向相同。
(3)由a=可知,F相同时,a越大说明运动状态越易改变,物体的惯性越小。
环节一:牛顿第二定律的表达式
例1 在平直路面上,质量为1 100 kg的汽车在进行研发测试,当速度达到100 km/h时取消动力,汽车经过70 s停了下来。汽车受到的阻力是多大 汽车重新起步加速时,牵引力为2 000 N,产生的加速度是多少 假定试车过程中汽车受到的阻力不变。
初速度为v0=100 km/h=27.8 m/s,末速度为0,滑行时间为t=70 s。
根据加速度的定义式得a==﹣0.397 m/s2,
根据牛顿第二定律得汽车受到的阻力为F阻=ma=﹣437 N。
重新起步后,汽车所受的合力为F合=F牵+F阻=1 563 N。
由牛顿第二定律可以得到汽车的加速度为a==1.42 m/s2,
重新起步产生的加速度的方向与运动方向相同。
环节二:牛顿第二定律的应用
例2 某同学在列车车厢的顶部用细线悬挂一个小球,
在列车以某一加速度渐渐启动的过程中,细线就会偏过一
定角度并相对车厢保持静止,通过测定偏角的大小就能确
定列车的加速度。在某次测定中,悬线与竖直方向的夹角
为θ,求列车的加速度。
设小球的质量为m,小球在竖直平面内受到重力mg、绳的拉力FT,在这两个力的作用下,小球产生水平方向的加速度a。这表明,FT与mg的合力方向水平向右。
根据牛顿第二定律得mgtan θ=ma,
解得a==gtan θ。
加速度的方向水平向右。
环节二:牛顿第二定律的应用
课堂练习
B
课堂练习
A
谢谢!
