第二十三章 旋转 单元练习(含答案) 2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十三章 旋转 单元练习(含答案) 2023—2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 198.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-04 18:54:32 | ||
图片预览

文档简介
第二十三章 旋转
一、选择题
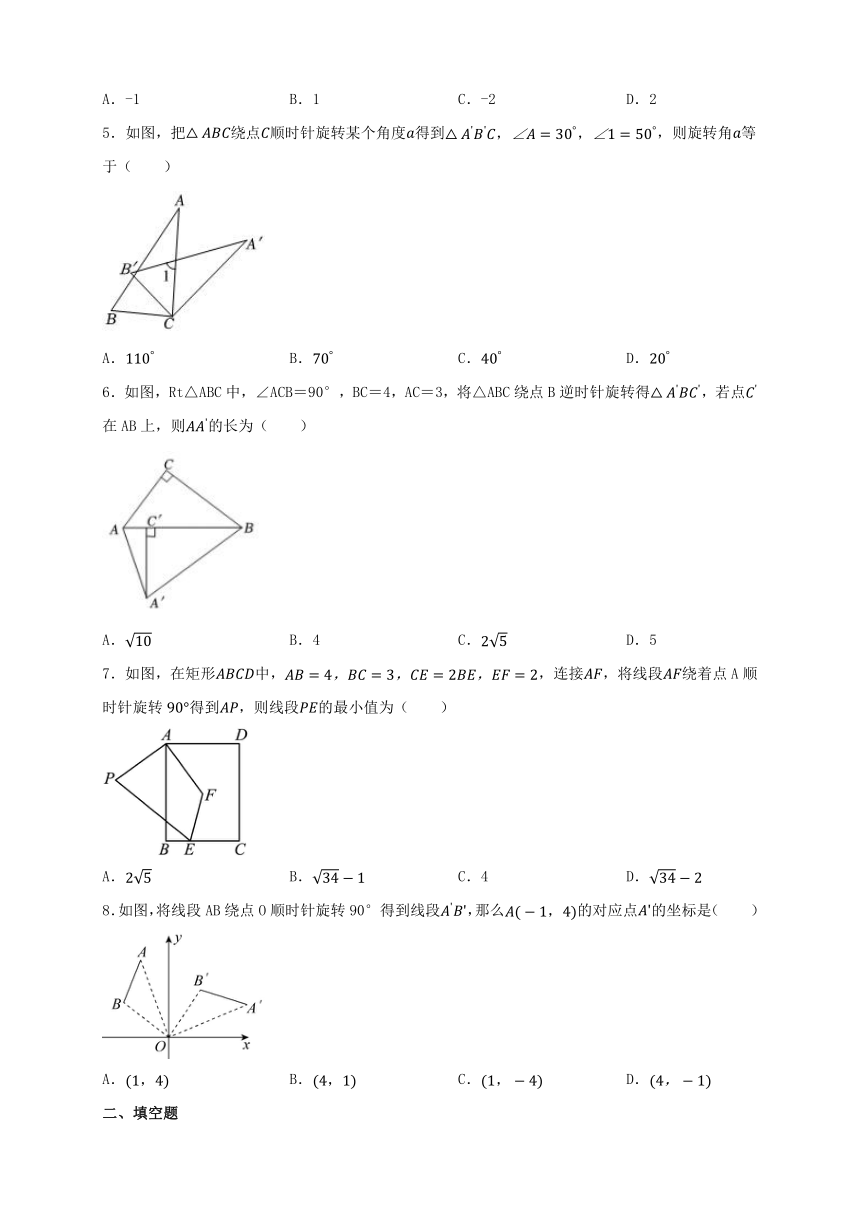
1.下列图形中,既是中心对称图形,又是轴对称图形的是( )
A. B.
C. D.
2.如图,△ABC经过变换得到△AB'C',其中△ABC绕点A逆时针旋转60°的是( )
A. B.
C. D.
3.如图,将正方形ABCD绕点D逆时针旋转90°后,点B的坐标变为( )
A. B. C. D.
4.已知点A(-1,a),点B(b,2)关于原点对称,则a+b的值是( )
A.-1 B.1 C.-2 D.2
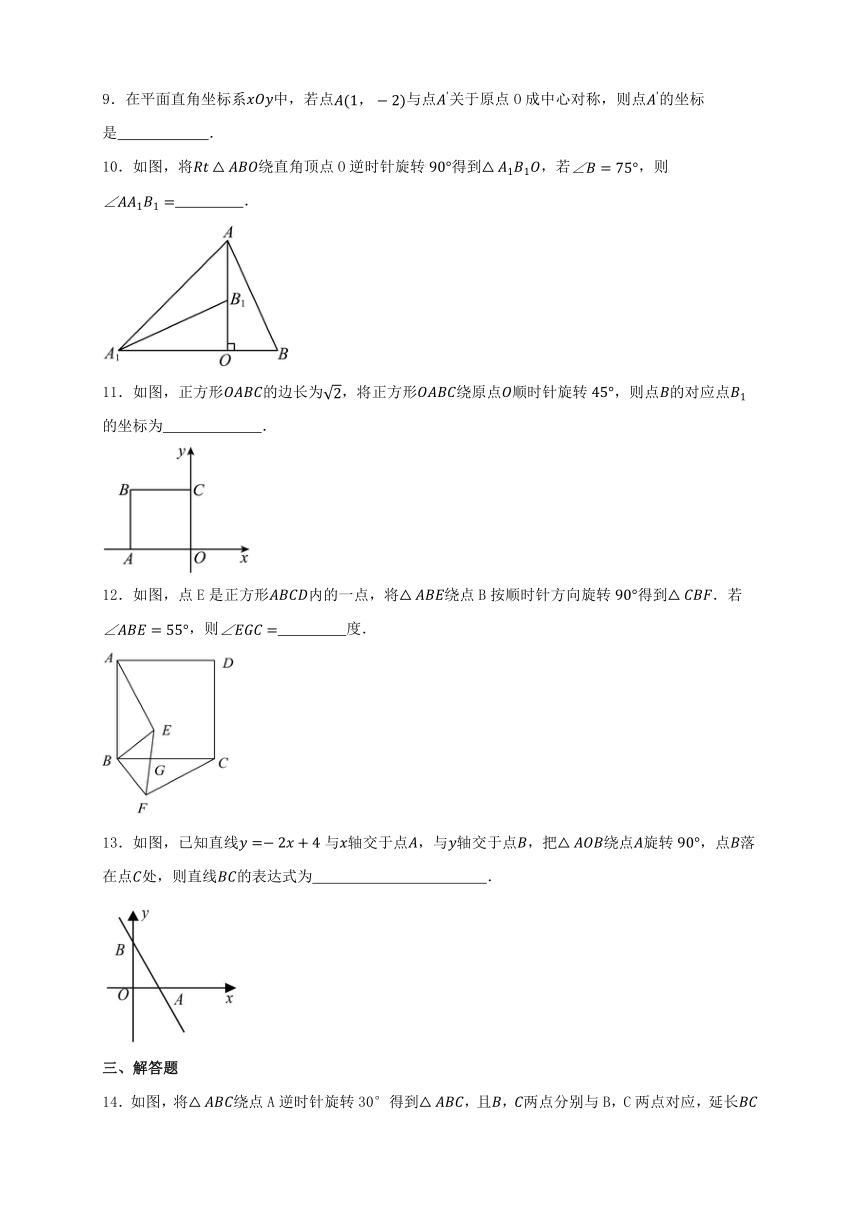
5.如图,把绕点顺时针旋转某个角度得到,则旋转角等于( )
A. B. C. D.
6.如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得,若点在AB上,则的长为( )
A. B.4 C. D.5
7.如图,在矩形中,,连接,将线段绕着点A顺时针旋转得到,则线段的最小值为( )
A. B. C.4 D.
8.如图,将线段AB绕点O顺时针旋转90°得到线段,那么的对应点的坐标是( )
A. B. C. D.
二、填空题
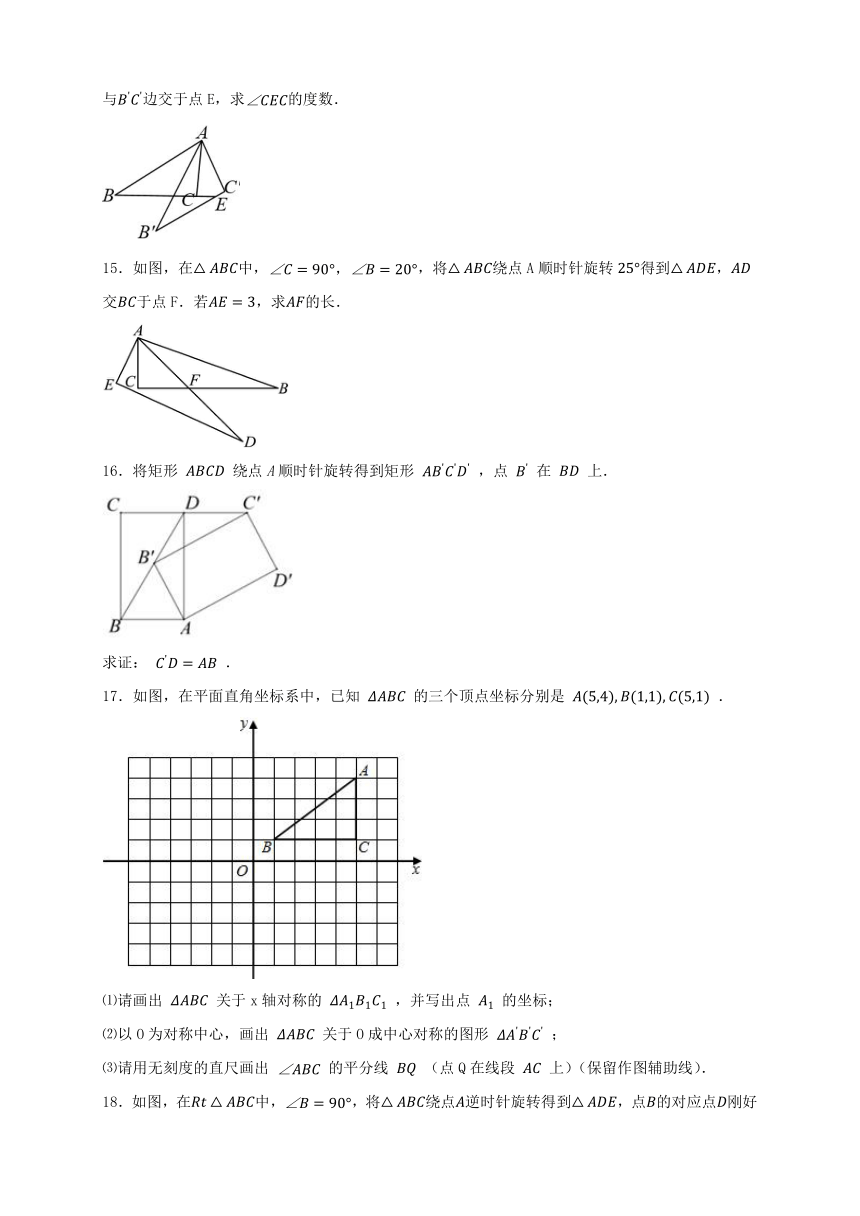
9.在平面直角坐标系中,若点与点关于原点O成中心对称,则点的坐标是 .
10.如图,将绕直角顶点O逆时针旋转得到,若,则 .
11.如图,正方形的边长为,将正方形绕原点顺时针旋转,则点的对应点的坐标为 .
12.如图,点E是正方形内的一点,将绕点B按顺时针方向旋转得到.若,则 度.
13.如图,已知直线与轴交于点,与轴交于点,把绕点旋转,点落在点处,则直线的表达式为 .
三、解答题
14.如图,将绕点A逆时针旋转30°得到,且,两点分别与B,C两点对应,延长与边交于点E,求的度数.
15.如图,在中,,将绕点A顺时针旋转得到,交于点F.若,求的长.
16.将矩形 绕点A顺时针旋转得到矩形 ,点 在 上.
求证: .
17.如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 .
⑴请画出 关于x轴对称的 ,并写出点 的坐标;
⑵以O为对称中心,画出 关于O成中心对称的图形 ;
⑶请用无刻度的直尺画出 的平分线 (点Q在线段 上)(保留作图辅助线).
18.如图,在中,,将绕点逆时针旋转得到,点的对应点刚好落在边上,连接.
(1)若,求的度数;
(2)若,,求四边形的面积.
19.将直角三角板OMN的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图,若∠BON=60°,求∠AOM的度数;
(2)若∠AOM=2∠COM,求∠AON的度数;
(3)将直角三角板OMN绕顶点O按逆时针方向旋转,在旋转过程中:当∠BON=120°时,求∠COM的度数.
参考答案
1.C
2.D
3.A
4.A
5.C
6.A
7.D
8.B
9.
10.30°
11.(0,2)
12.80
13.或
14.解:由旋转的性质可得,,
∵∠ACB+∠ACE=180°,
∴,
∴.
15.解:∵绕点A顺时针旋转得到,
∴.
∵,
∴.
∵,
∴.
∵,
∴是等腰直角三角形.
∴.
16.证明(方法不唯一):
由旋转可得, ,
,
又
又 ,
,
,
又 ,
.
17.解:(1)如图所示, 即为所求,点 的坐标为 ;
(2)如图所示;
(3)如图所示,在格点上分别取一点M、N,连接AN、CM,交于点J,作射线BJ,交AC于点Q,则BQ即为所求
18.(1)解:在,,
,
将绕点顺时针旋转得到,
,,
,
;
(2)解:在中,,
,
,
由旋转可得,,
,
.
19.(1)解:∵∠MON=90°,∠BON=60°,
∴∠AOM=180°-∠MON-∠BON=180°-90°-60°=30°.
(2)解:∵射线OC平分∠AON,
∴∠AON=2∠AOC,
设∠COM=x,则∠AOM=2x,
∴∠CON=∠AOC=∠COM+∠AOM=x+2x=3x,
∵∠COM+∠CON=90°,
∴x+3x=90°,
解之:x=22.5°;
∴∠AON=6x=6×22.5°=135°
(3)解:当NO在直线AB的上方时,
∵∠AON=180°-∠BON,
∴∠AON=60°,
∵OC平分∠AON,
∴∠CON=∠AON=30°,
∵∠MON=90°,
∴∠COM=∠MON-∠CON=90°-30°=60°;
当ON在直线AB的下方时,
∵∠AON=180°-∠BON,
∴∠AON=60°,
∵OC平分∠AON,
∴∠CON=30°,
∴∠COM=∠MON+∠CON=90°+30°=120°;
∴∠COM的度数为60°或120°
一、选择题
1.下列图形中,既是中心对称图形,又是轴对称图形的是( )
A. B.
C. D.
2.如图,△ABC经过变换得到△AB'C',其中△ABC绕点A逆时针旋转60°的是( )
A. B.
C. D.
3.如图,将正方形ABCD绕点D逆时针旋转90°后,点B的坐标变为( )
A. B. C. D.
4.已知点A(-1,a),点B(b,2)关于原点对称,则a+b的值是( )
A.-1 B.1 C.-2 D.2
5.如图,把绕点顺时针旋转某个角度得到,则旋转角等于( )
A. B. C. D.
6.如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得,若点在AB上,则的长为( )
A. B.4 C. D.5
7.如图,在矩形中,,连接,将线段绕着点A顺时针旋转得到,则线段的最小值为( )
A. B. C.4 D.
8.如图,将线段AB绕点O顺时针旋转90°得到线段,那么的对应点的坐标是( )
A. B. C. D.
二、填空题
9.在平面直角坐标系中,若点与点关于原点O成中心对称,则点的坐标是 .
10.如图,将绕直角顶点O逆时针旋转得到,若,则 .
11.如图,正方形的边长为,将正方形绕原点顺时针旋转,则点的对应点的坐标为 .
12.如图,点E是正方形内的一点,将绕点B按顺时针方向旋转得到.若,则 度.
13.如图,已知直线与轴交于点,与轴交于点,把绕点旋转,点落在点处,则直线的表达式为 .
三、解答题
14.如图,将绕点A逆时针旋转30°得到,且,两点分别与B,C两点对应,延长与边交于点E,求的度数.
15.如图,在中,,将绕点A顺时针旋转得到,交于点F.若,求的长.
16.将矩形 绕点A顺时针旋转得到矩形 ,点 在 上.
求证: .
17.如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 .
⑴请画出 关于x轴对称的 ,并写出点 的坐标;
⑵以O为对称中心,画出 关于O成中心对称的图形 ;
⑶请用无刻度的直尺画出 的平分线 (点Q在线段 上)(保留作图辅助线).
18.如图,在中,,将绕点逆时针旋转得到,点的对应点刚好落在边上,连接.
(1)若,求的度数;
(2)若,,求四边形的面积.
19.将直角三角板OMN的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图,若∠BON=60°,求∠AOM的度数;
(2)若∠AOM=2∠COM,求∠AON的度数;
(3)将直角三角板OMN绕顶点O按逆时针方向旋转,在旋转过程中:当∠BON=120°时,求∠COM的度数.
参考答案
1.C
2.D
3.A
4.A
5.C
6.A
7.D
8.B
9.
10.30°
11.(0,2)
12.80
13.或
14.解:由旋转的性质可得,,
∵∠ACB+∠ACE=180°,
∴,
∴.
15.解:∵绕点A顺时针旋转得到,
∴.
∵,
∴.
∵,
∴.
∵,
∴是等腰直角三角形.
∴.
16.证明(方法不唯一):
由旋转可得, ,
,
又
又 ,
,
,
又 ,
.
17.解:(1)如图所示, 即为所求,点 的坐标为 ;
(2)如图所示;
(3)如图所示,在格点上分别取一点M、N,连接AN、CM,交于点J,作射线BJ,交AC于点Q,则BQ即为所求
18.(1)解:在,,
,
将绕点顺时针旋转得到,
,,
,
;
(2)解:在中,,
,
,
由旋转可得,,
,
.
19.(1)解:∵∠MON=90°,∠BON=60°,
∴∠AOM=180°-∠MON-∠BON=180°-90°-60°=30°.
(2)解:∵射线OC平分∠AON,
∴∠AON=2∠AOC,
设∠COM=x,则∠AOM=2x,
∴∠CON=∠AOC=∠COM+∠AOM=x+2x=3x,
∵∠COM+∠CON=90°,
∴x+3x=90°,
解之:x=22.5°;
∴∠AON=6x=6×22.5°=135°
(3)解:当NO在直线AB的上方时,
∵∠AON=180°-∠BON,
∴∠AON=60°,
∵OC平分∠AON,
∴∠CON=∠AON=30°,
∵∠MON=90°,
∴∠COM=∠MON-∠CON=90°-30°=60°;
当ON在直线AB的下方时,
∵∠AON=180°-∠BON,
∴∠AON=60°,
∵OC平分∠AON,
∴∠CON=30°,
∴∠COM=∠MON+∠CON=90°+30°=120°;
∴∠COM的度数为60°或120°
同课章节目录
