第二十二章 二次函数 单元练习 (含答案)2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十二章 二次函数 单元练习 (含答案)2023—2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 50.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 08:43:33 | ||
图片预览

文档简介
第二十二章 二次函数
一、选择题
1.下列函数中,y关于x的二次函数的是( )
A.y=x3+2x2+3 B.y=﹣
C.y=x2+x D.y=mx2+x+1
2.已知一个二次函数y = ax2(a≠0)的图象经过(-2,8),则下列点中在该函数的图象上的是( )
A.(2,8) B.(1,3) C.( -1,3) D.(2,6)
3.二次函数的图象在这一段位于轴的下方,在这一段位于轴的上方,则的值为( )
A.1 B.-1 C.2 D.-2
4.若二次函数的图象经过A、B、C三点,则关于y1、y2、y3大小关系正确的是( )
A. B. C. D.
5.在二次函数y=x2-2x-3中,当时,y的最大值和最小值分别是( )
A.0,-4 B.0,-3 C.-3,-4 D.0,0
6.在二次函数y =x2+ 2x+1的图像上,若y随x的增大而增大,则x的取值范围是( )
A.x<1 B.x>1 C.x<-1 D.x>-1
7.如图,铅球的出手点 距地面1米,出手后的运动路线是抛物线,出手后4秒钟达到最大高度 米,则铅球运行路线的解析式为( )
A. B.
C. D.
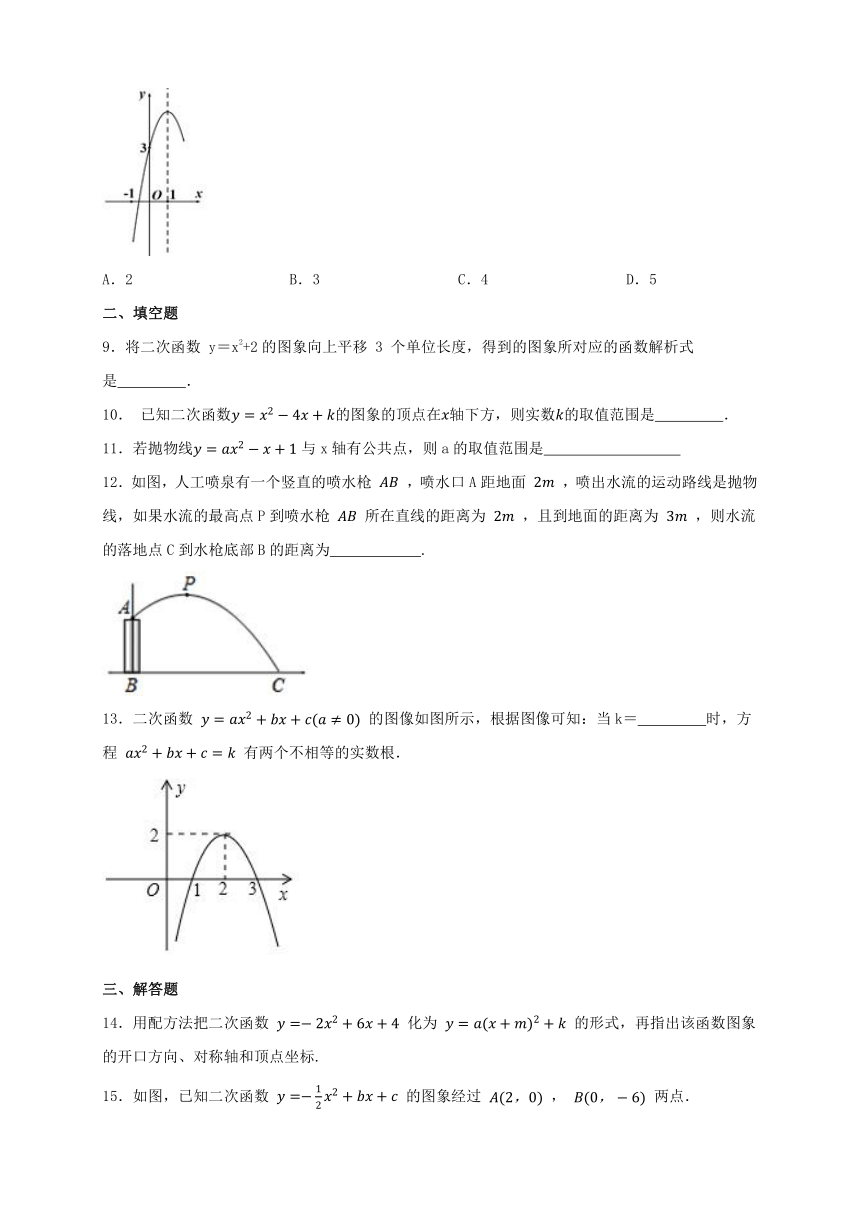
8.如图是抛物线 的部分图象,其对称轴为直线 ,与 轴的交点坐标为 ,下列结论:① ;② ;③方程 的两根分别是0和2;④方程 有一个实根大于2;⑤当 时, 随着 的增大而减小. 其中正确结论的个数是( )
A.2 B.3 C.4 D.5
二、填空题
9.将二次函数 y=x2+2的图象向上平移 3 个单位长度,得到的图象所对应的函数解析式是 .
10. 已知二次函数的图象的顶点在轴下方,则实数的取值范围是 .
11.若抛物线与x轴有公共点,则a的取值范围是
12.如图,人工喷泉有一个竖直的喷水枪 ,喷水口A距地面 ,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪 所在直线的距离为 ,且到地面的距离为 ,则水流的落地点C到水枪底部B的距离为 .
13.二次函数 的图像如图所示,根据图像可知:当k= 时,方程 有两个不相等的实数根.
三、解答题
14.用配方法把二次函数 化为 的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.
15.如图,已知二次函数 的图象经过 , 两点.
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与 轴交于点 ,连接 , ,求 的面积.
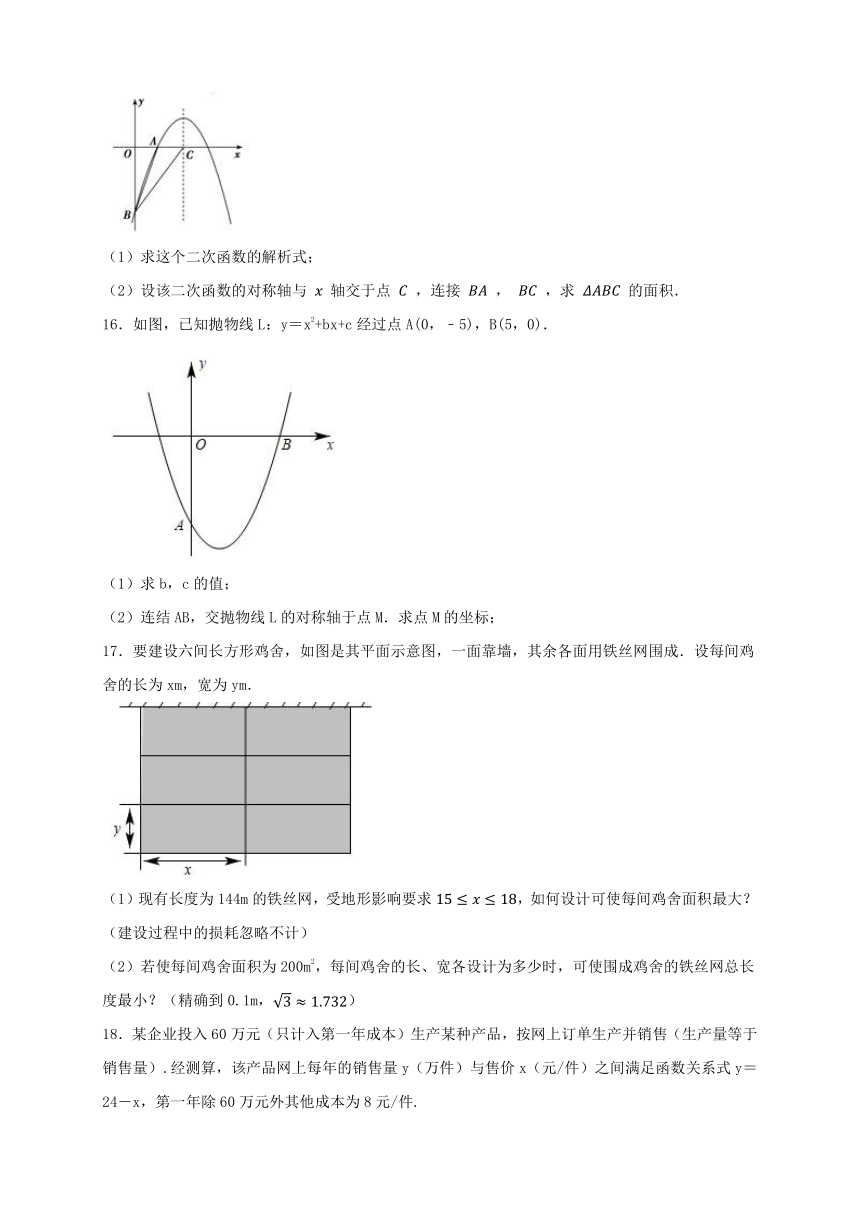
16.如图,已知抛物线L:y=x2+bx+c经过点A(0,﹣5),B(5,0).
(1)求b,c的值;
(2)连结AB,交抛物线L的对称轴于点M.求点M的坐标;
17.要建设六间长方形鸡舍,如图是其平面示意图,一面靠墙,其余各面用铁丝网围成.设每间鸡舍的长为xm,宽为ym.
(1)现有长度为144m的铁丝网,受地形影响要求,如何设计可使每间鸡舍面积最大?(建设过程中的损耗忽略不计)
(2)若使每间鸡舍面积为200m2,每间鸡舍的长、宽各设计为多少时,可使围成鸡舍的铁丝网总长度最小?(精确到0.1m,)
18.某企业投入60万元(只计入第一年成本)生产某种产品,按网上订单生产并销售(生产量等于销售量).经测算,该产品网上每年的销售量y(万件)与售价x(元/件)之间满足函数关系式y=24-x,第一年除60万元外其他成本为8元/件.
(1)求该产品第一年的利润w(万元)与售价x之间的函数关系式;
(2)该产品第一年利润为4万元,第二年将它全部作为技改资金再次投入(只计入第二年成本)后,其他成本下降2元/件.①求该产品第一年的售价;②若第二年售价不高于第一年,销售量不超过13万件,则第二年利润最少是多少万元?
参考答案
1.C
2.A
3.A
4.C
5.A
6.D
7.C
8.C
9.y=x2+5
10.
11.且
12.
13.k<2
14.解: ,
= ,
= ,
开口向下,对称轴为直线 ,顶点
15.(1)解:把 , 代入 得
,
解得 .
∴这个二次函数解析式为 .
(2)解:∵抛物线对称轴为直线 ,
∴ 的坐标为 ,
∴ ,
∴ .
16.(1)解:将点A、点B坐标代入函数解析式可得:
,
解得: ,
∴ , ;
(2)解:设直线AB的解析式为: ,
将点A、点B坐标代入函数解析式可得:
,
解得: ,
∴一次函数解析式为: ,
由(1)得二次函数解析式为: ,
对称轴为: ,
直线 与 的交点为M,
∴当 时, ,
∴交点M的坐标为(2,-3).
17.(1)解:由条件知:,即①.
设每间鸡舍的面积为S,则.把①代入得
根据二次函数的性质,当时,关于x的函数S的图象自左向右下降,S随x的增大而减小,又要求,所以时,S取最大值为90,
此时,每间鸡舍长为15m,宽为6m,每间面积最大为90m2.
(2)解:由条件知.设铁丝网总长为l,则.
由,得.
.
由非负数的性质当且仅当,等号成立,
此时,,.
故每间鸡舍长为,宽为m时,可使铁丝网总长最小.
18.(1)解:由题意得:
(2)解:①由(1)得:当 时,
则 即
解得:
即第一年的售价为每件16元,
② 第二年售价不高于第一年,销售量不超过13万件,
解得:
其他成本下降2元/件,
∴
对称轴为
当 时,利润最高,为77万元,而
当 时, (万元)
当 时, (万元)
所以第二年的最低利润为 万元.
一、选择题
1.下列函数中,y关于x的二次函数的是( )
A.y=x3+2x2+3 B.y=﹣
C.y=x2+x D.y=mx2+x+1
2.已知一个二次函数y = ax2(a≠0)的图象经过(-2,8),则下列点中在该函数的图象上的是( )
A.(2,8) B.(1,3) C.( -1,3) D.(2,6)
3.二次函数的图象在这一段位于轴的下方,在这一段位于轴的上方,则的值为( )
A.1 B.-1 C.2 D.-2
4.若二次函数的图象经过A、B、C三点,则关于y1、y2、y3大小关系正确的是( )
A. B. C. D.
5.在二次函数y=x2-2x-3中,当时,y的最大值和最小值分别是( )
A.0,-4 B.0,-3 C.-3,-4 D.0,0
6.在二次函数y =x2+ 2x+1的图像上,若y随x的增大而增大,则x的取值范围是( )
A.x<1 B.x>1 C.x<-1 D.x>-1
7.如图,铅球的出手点 距地面1米,出手后的运动路线是抛物线,出手后4秒钟达到最大高度 米,则铅球运行路线的解析式为( )
A. B.
C. D.
8.如图是抛物线 的部分图象,其对称轴为直线 ,与 轴的交点坐标为 ,下列结论:① ;② ;③方程 的两根分别是0和2;④方程 有一个实根大于2;⑤当 时, 随着 的增大而减小. 其中正确结论的个数是( )
A.2 B.3 C.4 D.5
二、填空题
9.将二次函数 y=x2+2的图象向上平移 3 个单位长度,得到的图象所对应的函数解析式是 .
10. 已知二次函数的图象的顶点在轴下方,则实数的取值范围是 .
11.若抛物线与x轴有公共点,则a的取值范围是
12.如图,人工喷泉有一个竖直的喷水枪 ,喷水口A距地面 ,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪 所在直线的距离为 ,且到地面的距离为 ,则水流的落地点C到水枪底部B的距离为 .
13.二次函数 的图像如图所示,根据图像可知:当k= 时,方程 有两个不相等的实数根.
三、解答题
14.用配方法把二次函数 化为 的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.
15.如图,已知二次函数 的图象经过 , 两点.
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与 轴交于点 ,连接 , ,求 的面积.
16.如图,已知抛物线L:y=x2+bx+c经过点A(0,﹣5),B(5,0).
(1)求b,c的值;
(2)连结AB,交抛物线L的对称轴于点M.求点M的坐标;
17.要建设六间长方形鸡舍,如图是其平面示意图,一面靠墙,其余各面用铁丝网围成.设每间鸡舍的长为xm,宽为ym.
(1)现有长度为144m的铁丝网,受地形影响要求,如何设计可使每间鸡舍面积最大?(建设过程中的损耗忽略不计)
(2)若使每间鸡舍面积为200m2,每间鸡舍的长、宽各设计为多少时,可使围成鸡舍的铁丝网总长度最小?(精确到0.1m,)
18.某企业投入60万元(只计入第一年成本)生产某种产品,按网上订单生产并销售(生产量等于销售量).经测算,该产品网上每年的销售量y(万件)与售价x(元/件)之间满足函数关系式y=24-x,第一年除60万元外其他成本为8元/件.
(1)求该产品第一年的利润w(万元)与售价x之间的函数关系式;
(2)该产品第一年利润为4万元,第二年将它全部作为技改资金再次投入(只计入第二年成本)后,其他成本下降2元/件.①求该产品第一年的售价;②若第二年售价不高于第一年,销售量不超过13万件,则第二年利润最少是多少万元?
参考答案
1.C
2.A
3.A
4.C
5.A
6.D
7.C
8.C
9.y=x2+5
10.
11.且
12.
13.k<2
14.解: ,
= ,
= ,
开口向下,对称轴为直线 ,顶点
15.(1)解:把 , 代入 得
,
解得 .
∴这个二次函数解析式为 .
(2)解:∵抛物线对称轴为直线 ,
∴ 的坐标为 ,
∴ ,
∴ .
16.(1)解:将点A、点B坐标代入函数解析式可得:
,
解得: ,
∴ , ;
(2)解:设直线AB的解析式为: ,
将点A、点B坐标代入函数解析式可得:
,
解得: ,
∴一次函数解析式为: ,
由(1)得二次函数解析式为: ,
对称轴为: ,
直线 与 的交点为M,
∴当 时, ,
∴交点M的坐标为(2,-3).
17.(1)解:由条件知:,即①.
设每间鸡舍的面积为S,则.把①代入得
根据二次函数的性质,当时,关于x的函数S的图象自左向右下降,S随x的增大而减小,又要求,所以时,S取最大值为90,
此时,每间鸡舍长为15m,宽为6m,每间面积最大为90m2.
(2)解:由条件知.设铁丝网总长为l,则.
由,得.
.
由非负数的性质当且仅当,等号成立,
此时,,.
故每间鸡舍长为,宽为m时,可使铁丝网总长最小.
18.(1)解:由题意得:
(2)解:①由(1)得:当 时,
则 即
解得:
即第一年的售价为每件16元,
② 第二年售价不高于第一年,销售量不超过13万件,
解得:
其他成本下降2元/件,
∴
对称轴为
当 时,利润最高,为77万元,而
当 时, (万元)
当 时, (万元)
所以第二年的最低利润为 万元.
同课章节目录
