平行的判定及性质综合应用
图片预览




文档简介
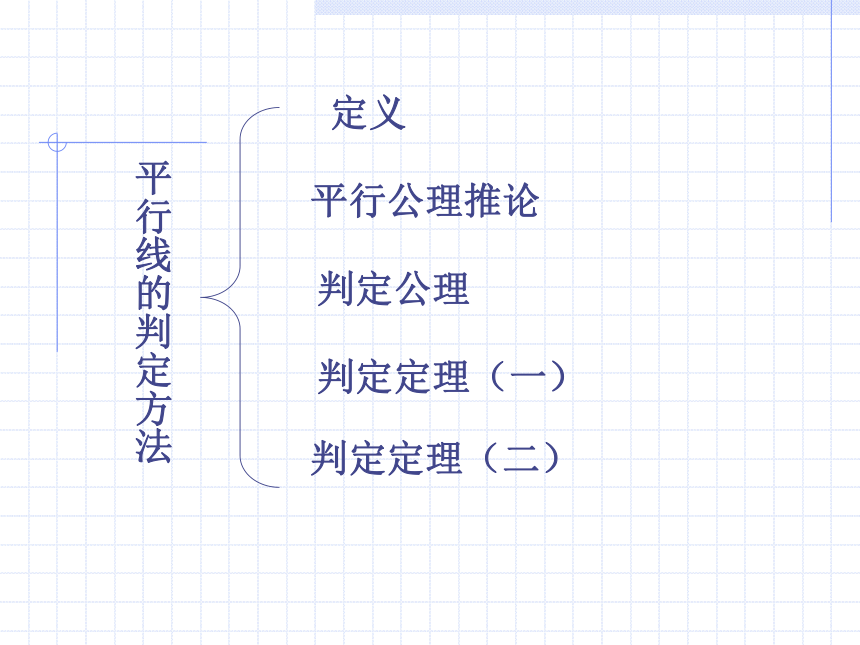
课件13张PPT。平行线的性质与判定的综合应用平行公理及推论平行线的判定平行线的性质一、知识结构定义平行公理推论判定公理判定定理(一)判定定理(二)平行线的判定方法平行线的性质:两直线平行同位角相等内错角相等同旁内角互补基础训练:
1、选择:
(1)α和β是同旁内角,若∠α=50°,则∠β的度数为 ( )
(A)50 ° (B)130 °
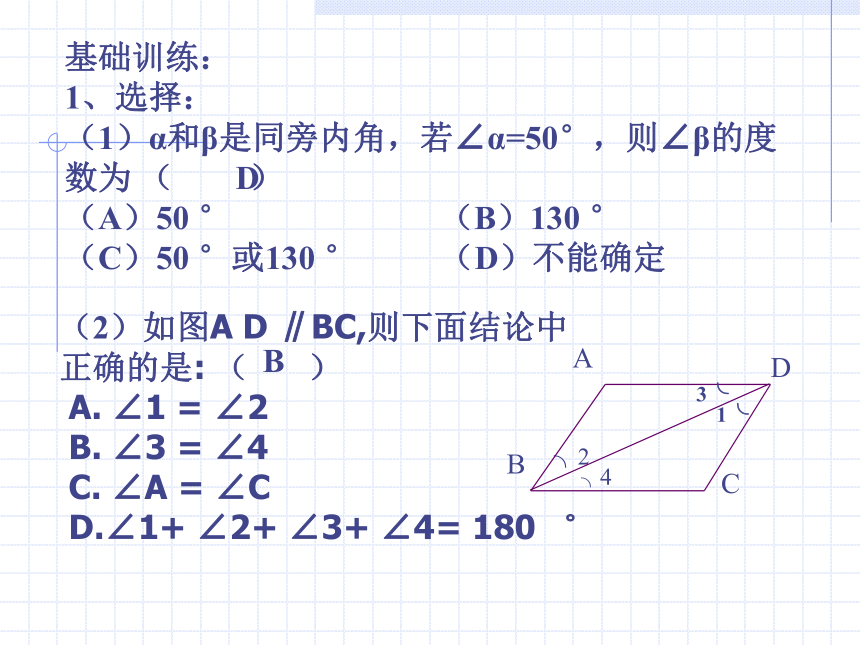
(C)50 °或130 ° (D)不能确定(2)如图A D ∥BC,则下面结论中正确的是: ( )
A. ∠1 = ∠2
B. ∠3 = ∠4
C. ∠A = ∠C
D.∠1+ ∠2+ ∠3+ ∠4= 180 ゜DB (4)如图,AB∥CD ∥EF,BC ∥AD,AC为∠BAD的平分线,图中与∠AOF相等的角有( ) (A)2个 (B)3个
(C)4个 (D)5个BD (5)如图,∠1= ∠2=45 °,∠3=70 °,则∠4等于( )
(A)70 ° (B)110 °
(C)45 ° (D)35°2、填空:
(1)如图,如果AD ∥BC,那么可以推出哪些结论?把可推出的结论都写出来
__________________________________B答:∠EAD= ∠B, ∠DAC= ∠C,
∠DAB+∠B=180 °证明:∵ ∠1= ∠2(已知)
∠1= ∠3, ∠2= ∠4 ( )
∴ ∠3= ∠4(等量代换)
∴___ ∥ _____( )
∴ ∠C=______ ( )
∵ ∠C= ∠D (已知)
∴∠D=________( )
∴DF∥AC ( )对顶角相等内错角相等,两直线平行∠ABD∠ABD两直线平行,同位角相等等量代换内错角相等,两直线平行 E点为DF上的点,B为AC上的点,
∠1= ∠2, ∠C= ∠D,求证:DF ∥AC (3)某人从点A向南偏东40 °走到点B,再自点B向北偏西75 °走到点C,则∠ABC=____°. (4)货船沿北偏西62 °方向航行,后因避礁先向右拐28 °,再向左拐28 °,这时货船沿____________方向前进。北偏西62 ° (5) .如图, AB∥CD ,直线EF分别交AB,CD于点E、F,EG平分∠BEF,若∠1=72 °
则∠2= _________35∠3=54 °如图,已知:AB∥CD, ∠1=∠2.
说明BE∥CF的理由.1.如图,已知:AB∥CD,∠1=55°∠2=80°, 求∠3的度数. 2.如图,已知:AB∥CD,∠A=70°∠DHE=70°,试说明AM∥EF平行公理及推论平行线的判定平行线的性质平行线的意义判定公理判定定理性质公理性质定理知识结构定义平行公理推论判定公理判定定理(一)判定定理(二)平行线的判定方法两直线平行同位角相等内错角相等同旁内角互补平行线的性质
1、选择:
(1)α和β是同旁内角,若∠α=50°,则∠β的度数为 ( )
(A)50 ° (B)130 °
(C)50 °或130 ° (D)不能确定(2)如图A D ∥BC,则下面结论中正确的是: ( )
A. ∠1 = ∠2
B. ∠3 = ∠4
C. ∠A = ∠C
D.∠1+ ∠2+ ∠3+ ∠4= 180 ゜DB (4)如图,AB∥CD ∥EF,BC ∥AD,AC为∠BAD的平分线,图中与∠AOF相等的角有( ) (A)2个 (B)3个
(C)4个 (D)5个BD (5)如图,∠1= ∠2=45 °,∠3=70 °,则∠4等于( )
(A)70 ° (B)110 °
(C)45 ° (D)35°2、填空:
(1)如图,如果AD ∥BC,那么可以推出哪些结论?把可推出的结论都写出来
__________________________________B答:∠EAD= ∠B, ∠DAC= ∠C,
∠DAB+∠B=180 °证明:∵ ∠1= ∠2(已知)
∠1= ∠3, ∠2= ∠4 ( )
∴ ∠3= ∠4(等量代换)
∴___ ∥ _____( )
∴ ∠C=______ ( )
∵ ∠C= ∠D (已知)
∴∠D=________( )
∴DF∥AC ( )对顶角相等内错角相等,两直线平行∠ABD∠ABD两直线平行,同位角相等等量代换内错角相等,两直线平行 E点为DF上的点,B为AC上的点,
∠1= ∠2, ∠C= ∠D,求证:DF ∥AC (3)某人从点A向南偏东40 °走到点B,再自点B向北偏西75 °走到点C,则∠ABC=____°. (4)货船沿北偏西62 °方向航行,后因避礁先向右拐28 °,再向左拐28 °,这时货船沿____________方向前进。北偏西62 ° (5) .如图, AB∥CD ,直线EF分别交AB,CD于点E、F,EG平分∠BEF,若∠1=72 °
则∠2= _________35∠3=54 °如图,已知:AB∥CD, ∠1=∠2.
说明BE∥CF的理由.1.如图,已知:AB∥CD,∠1=55°∠2=80°, 求∠3的度数. 2.如图,已知:AB∥CD,∠A=70°∠DHE=70°,试说明AM∥EF平行公理及推论平行线的判定平行线的性质平行线的意义判定公理判定定理性质公理性质定理知识结构定义平行公理推论判定公理判定定理(一)判定定理(二)平行线的判定方法两直线平行同位角相等内错角相等同旁内角互补平行线的性质
