思维拓展:小数除法(试题)数学五年级上册北师大版(含答案)
文档属性
| 名称 | 思维拓展:小数除法(试题)数学五年级上册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 20:47:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
思维拓展:小数除法(试题)数学五年级上册北师大版
一、选择题
1.按规律填数:18,9,4.5,2.25,1.125,( ),0.28125,…
A.0.5625 B.0.125 C.0.65 D.0.5635
2.要使商小于,里应填( )的数。
A. B. C. D.
3.45米长的绳子,每3.7米截成一段,结果是( )。
A.12段余0.6米 B.12段余6米 C.12段
4.用1000元人民币兑换欧元,算式是( )。(1欧元兑换人民币7.2元)
A.1000÷7.2 B.1000×7.2 C.1000×1 D.7.2÷1000
5.做一套校服需要1.9m布,20m最多可做( )套这样的校服。
A.10 B.11 C.12
6.李阿姨买了14个橘子共重2.1千克,如果买这样的橘子11千克,大约( )个。
A.不到50个 B.100个以上 C.70多个 D.不到60个
二、填空题
7.10.6÷6的商用循环小数表示是( ),保留两位小数是( )。
8.被除数扩大到原来的6倍,除数扩大到原来的3倍,商( )倍。
9.完成下表,电价按每千瓦时0.48元计算(得数保留两位小数)。
名称 每时耗电 量/千瓦时 每日耗电量/千瓦时 (按24小时计算) 每年耗电量/千瓦时 (按365天算) 每年所交电费/元 (按365天算)
冰箱 普通型 0.04 ( ) ( ) ( )
节能型 0.02 ( ) ( ) ( )
10.做一个水桶需要铁皮3.4m2,22.8m2的铁皮最多能做( )个水桶。
11.计算下面各题,说说你发现了什么?
0.32÷0.8=( ) 8÷0.4=( )
5.2÷1=( ) 3.67÷1=( )
80÷1.6=( ) 7.2÷1.2=( )
我发现:在小数除法的算式中,当除数大于1时,商( )被除数;当除数小于1时,商( )被除数。
12.循环小数0.ABCABC…的小数部分前60位上的数字和是100,这个循环小数的循环节是( )时这个循环小数最大,是( )时这个循环小数最小。(A、B、C为三个不同的自然数)
13.要使□.24÷6的商大于1,方框里可填( );如果商小于1,方框里可填( )。
14.贝贝心里想了一个数,于是她把这个数与它自己相加、相减、相除,所得的和、差、商加起来是10.6。贝贝心里想的数是( )。
三、解答题
15.一个没有拧紧的水龙头每天大约滴水1.8千克,请计算:
(1)一年(按365 天计算)浪费多少千克水?
(2)把这些水分装在饮水桶中(每桶水约重15千克),大约能装多少桶?
16.王乐在计算6.4除以一个数时,由于商的小数点向右点错了一位,结果是40,这道题的除数是多少?
17.校办工厂原来有3台制钉机,每小时可以制钉24.3千克.现在又增加了同样的制钉机2台,每小时一共可以制钉多少千克
18.甲、乙两袋大米的总质量是26.8千克,如果从甲袋中取出3.2千克放入乙袋,这时两袋大米的质量相等,原来甲、乙两袋大米各重多少千克?
19.同学们去爬枫叶山。已知同学们上山平均速度是每小时1.5千米,上山用了3小时;沿原路下山,下山用时2小时。那么同学们上山和下山的平均速度是多少?
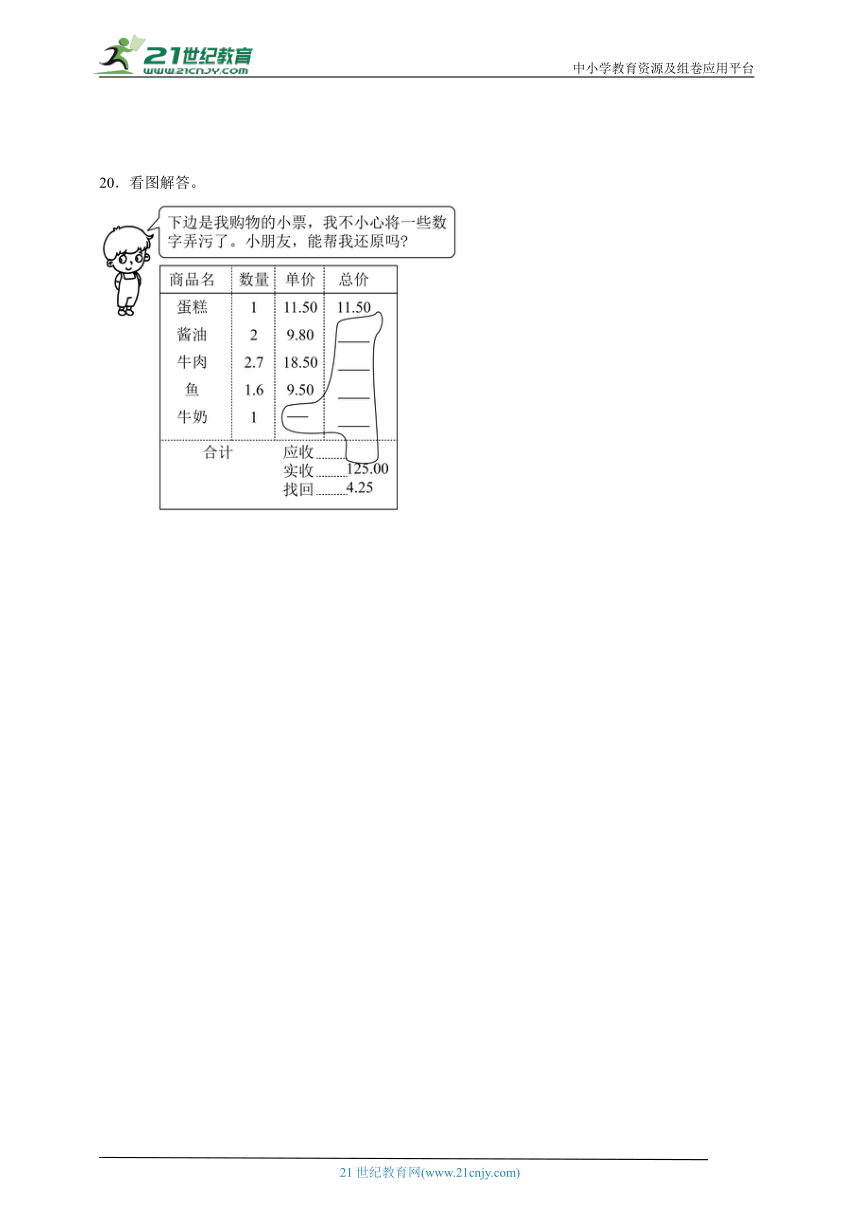
20.看图解答。
参考答案:
1.A
【分析】根据题意可知,9=18÷2;4.5=9÷2,2.25=4.5÷2,…,由此可知,后一个数是前一个数的一半,用前一个数除以2,即可求出后一个数,据此解答。
【详解】1.125÷2=0.5625
按规律填数:18,9,4.5,2.25,1.125,0.5625,0.28125,…
故答案为:A
【点睛】解答本题的关键是根据已知的数得出前后数之间的变化规律,再利用变化规律进行解答。
2.A
【分析】根据题意,结合小数除法的计算法则可知,当4□.38的整数部分小于45时,4□.38÷45的商小于1。据此解题。
【详解】要使4□.38÷45的商小于1,□里应填小于5的数,即:0、1、2、3、4。
故答案为:A
【点睛】本题考查了小数除法,掌握小数除法的计算法则是解题的关键。
3.A
【分析】根据除法的意义,用45除以3.7即可求出共可以截成几段;用每段绳子的长度乘段数即可求出截去多少米,再用绳子的总长度减去截去的长度即可求出还剩下多少米。
【详解】45÷3.7≈12(段)
45-12×3.7
=45-44.4
=0.6(米)
则45米长的绳子,每3.7米截成一段,结果是12段余0.6米。
故答案为:A
【点睛】本题考查小数除法,明确小数除法的计算方法是解题的关键。
4.A
【分析】由于1欧元兑换人民币7.2元,则看1000元人民币里面有多少个7.2,有多少个7.2就能兑换多少个欧元,即1000÷7.2,由此即可选择。
【详解】由分析可知:1000÷7.2≈138.89(欧元)
故答案为:A。
【点睛】此题主要考查人民币的兑换方法,同时熟练掌握除法的意义是解题的关键。
5.A
【分析】求20米布可以做多少套校服,就是求20米里面有几个1.9米,用20除以1.9即可求解。
【详解】20÷1.9≈10(套)
故答案为:A
【点睛】解答此题应根据求一个数里面含有几个另一个数,用除法解答;注意:应结合实际情况,用“去尾”法。
6.C
【分析】14个橘子共2.1千克,用2.1千克除以14个,求出每个橘子的质量,再用11千克除以每个橘子的质量,即可求出11千克橘子的个数。
【详解】11÷(2.1÷14)
=11÷0.15
≈73(个)
买这样的橘子11千克,大约有70多个。
故答案为:C
【点睛】解决本题先根据除法平均分的意义求出每个橘子的质量,再根据除法的包含意义求解。
7. 1.77
【分析】计算出10.6÷6的商,找出循环节;根据循环小数的简写方法:在循环节的首位和末位的上面各记一个小圆点即可;将此数保留两位小数,就是精确到百分位,看千分位上的数,再运用“四舍五入”的方法求出近似数即可;据此进行解答。
【详解】10.6÷6=1.766……
1.766……=
≈1.77
【点睛】本题考查循环小数的简写,以及小数的近似数的求法。
8.扩大到原来的2
【分析】除数不变,被除数扩大几倍或缩小到原来的几分之一,商也同样扩大几倍或缩小到原来的几分之一;被除数不变,除数扩大几倍或缩小到原来的几分之一(0除外),商反而缩小到原来的几分之一或扩大相同的倍数。所以被除数扩大到原来的6倍,除数扩大到原来的3倍,商先扩大到原来的6倍,再缩小,也就是将商扩大到原来的(6÷3)倍。
【详解】6÷3=2
被除数扩大到原来的6倍,除数扩大到原来的3倍,商扩大到原来的2倍。
【点睛】掌握商的变化规律是解答本题的关键。
9.见详解
【分析】普通型冰箱:用普通型冰箱每小时耗电量×24小时,求出每日的耗电量;
再用每日的耗电量×365天,求出每年的耗电量;
再用每年耗电量×每千瓦时0.48元,即可求出普通型冰箱每年所交电费的钱数;
节能型冰箱:用节能型冰箱每小时耗电量×24小时,求出每日的耗电量;
再用每日的耗电量×365天,求出每年的耗电量;
再用每年耗电量×每千瓦时0.48元,即可求出节能型冰箱每年所交电费的钱数;
保留几位小数,就看保留小数的下一位小数,再根据“四舍五入”法进行解答。
【详解】普通型冰箱:0.04×24=0.96(千瓦时)
0.96×365=350.4(千瓦时)
350.4×0.48≈168.19(元)
节能型冰箱:0.02×24=0.48(千瓦时)
0.48×365=175.2(千瓦时)
175.2×0.48≈84.10(元)
名称 每时耗电 量/千瓦时 每日耗电量/千瓦时 (按24小时计算) 每年耗电量/千瓦时 (按365天算) 每年所交电费/元 (按365天算)
冰箱 普通型 0.04 0.96 350.4 168.19
节能型 0.02 0.48 175.2 84.10
【点睛】本题考查小数与整数的乘法计算,小数与小数的乘法计算,以及“四舍五入”法的应用。
10.6
【分析】根据题意,做一个水桶需要铁皮3.4m2,求22.8m2铁皮最多能做多少个水桶,就是求22.8里有多少个3.4,用除法计算,结果用去尾法保留整数。
【详解】22.8÷3.4≈6(个)
做一个水桶需要铁皮3.4m2,22.8m2的铁皮最多能做6个水桶。
【点睛】本题考查除数是小数的除法,注意结果用“去尾法”解答。
11. 0.4 20 5.2 3.67 50 6 小于 大于
【分析】计算小数除法时,先移动除数的小数点使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数末尾添0补足),然后按照除数是整数的小数除法进行计算;
先根据小数除法计算的方法求出各个题目的商,再观察算式中除数与1的大小关系,以及被除数与商的大小关系,从而找出规律。
【详解】由分析可得:
0.32÷0.8=0.4 8÷0.4=20
5.2÷1=5.2 3.67÷1=3.67
80÷1.6=50 7.2÷1.2=6
观察算式,可以发现:
一个数(0除外),除以大于1的数,商小于这个数;
一个数(0除外),除以等于1的数,商等于这个数;
一个数(0除外),除以小于1的数,商大于这个数;
综上所述:在小数除法的算式中,当除数大于1时,商小于被除数;当除数小于1时,商大于被除数。
【点睛】本题考查了小数除法的应用,要求熟悉被除数和除数以及商之间的关系,并且了解它们之间的变化规律。
12. 410 023
【分析】根据题意,这个循环小数的循环节是ABC,又因为小数部分前60位上的数字和是100,所以60÷3×(A+B+C)=100,由此可得A+B+C的数值,因为A、B、C为三个不同的自然数,可以列举出三个字母各自代替的数字,据此答题即可。
【详解】由分析可得:
60÷3×(A+B+C)=100
60÷3×(A+B+C)×3=100×3
60×(A+B+C)=300
A+B+C=300÷60
A+B+C=5
因为A、B、C为三个不同的自然数,所以这三个数只能分别是0、2、3或0、1、4,要想循环小数最大,让A最大,B第二大,C最小,即A=4,B=1,C=0,此时该循环小数为0.410410…,要想循环小数最小,则A最小,B第二小,C最大,即A=0,B=2,C=3,此时该循环小数为0.023023…。
综上所述:循环小数0.ABCABC…的小数部分前60位上的数字和是100,这个循环小数的循环节是410时这个循环小数最大,是023时这个循环小数最小。
【点睛】本题主要考查简单周期现象中的规律问题,关键是利用循环小数的特点做题。
13. 6,7,8,9 0,1,2,3,4,5
【分析】根据题意可知,除数是6,要使商大于1,□内的数大于或等于6;如果商小于1,□内的数小于6,据此解答。
【详解】□.24÷6的商大于1,□内可以填:6,7,8,9;
□.24÷6的商小于1,□内可以填:0,1,2,3,4,5。
要使□.24÷6的商大于1,方框里可填7,8,9;如果商小于1,方框里可填0,1,2,3,4,5。
【点睛】明确被除数与除数之间大小关系是解答本题的关键。
14.4.8
【分析】设这个数为x,相加为2x,相减为0,相除为1;2x加1等于10.6,由此列方程为2x+1=10.6,解方程即可。
【详解】解:设这个数为x,根据题意可得:
2x+(x-x)+x÷x=10.6
2x+1=10.6
2x=9.6
2x÷2=9.6÷2
x=4.8
贝贝心里想的数是4.8。
【点睛】解答此题的关键是理解和、差、商的意义,明确:两个相同的数差为0、商为1。
15.(1)657千克(2)44桶
【详解】(1)1.8×365=657(千克)
答:一年浪费657千克水
(2)657÷15=43.8(桶)≈44(桶)
答:大约能装44桶水
16.1.6
【详解】6.4÷4=1.6;
答:这道题的除数是1.6.
【点睛】因为商的小数点向右点错了一位,即商扩大了10倍,结果是40,正确的商应为4,求被除数,根据“被除数÷除数=商”进行解答即可.
17.40.5千克
【详解】解法1:
24.3÷3×(3+2)
=24.3÷3×5
=8.1×5
=40.5(千克)
解法2:24.3+24.3÷3×2
=24.3+8.1×2
=24.3+16.2
=40.5(千克)
答:每小时一共可以制钉40.5千克.
【点睛】解法1:先求出每台制钉机每小时制钉的重量,然后用每台制钉机每小时制钉的重量乘现在制钉机的台数即可求出现在每小时一共可以制钉的重量;解法2:用每台制钉机每小时制钉的重量乘2,再加上原来3台制钉的总重量就是现在一共可以制钉的重量.
18.甲: 16.6千克;乙:10.2千克
【详解】26.8÷2=13.4(千克) 甲:13.4+3.2=16.6(千克)
乙:13.4-3.2=10.2(千克)
19.1.8千米/小时
【分析】根据速度×时间=路程,把数代入公式即可求出上山的路程:1.5×3=4.5(千米),由于同学们上山和下山总共走了4.5×2=9(千米),用时:3+2=5(小时),根据公式:速度=路程÷时间,把数代入公式即可求解。
【详解】1.5×3×2÷(3+2)
=4.5×2÷5
=9÷5
=1.8(千米/时)
答:同学们上山和下山的平均速度是1.8千米/时。
【点睛】本题主要考查行程问题的公式,熟练掌握它的公式并灵活运用,求出往返的路程和时间是解题的关键。
20.见详解
【分析】根据单价×数量=总价,据此分别求出酱油、牛肉、鱼的总价;用实收的钱数减去找回的钱数即可求出应收的钱数,再用应收的钱数减去蛋糕、酱油、牛肉和鱼的总价,即可求出牛奶的总价,再根据总价÷数量=单价,据此求出牛奶的单价;。
【详解】(元)
(元)
(元)
(元)
(元)
24.5÷1=24.5(元)
如图所示:
【点睛】本题考查小数乘法,明确总价、数量和单价之间的关系是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:小数除法(试题)数学五年级上册北师大版
一、选择题
1.按规律填数:18,9,4.5,2.25,1.125,( ),0.28125,…
A.0.5625 B.0.125 C.0.65 D.0.5635
2.要使商小于,里应填( )的数。
A. B. C. D.
3.45米长的绳子,每3.7米截成一段,结果是( )。
A.12段余0.6米 B.12段余6米 C.12段
4.用1000元人民币兑换欧元,算式是( )。(1欧元兑换人民币7.2元)
A.1000÷7.2 B.1000×7.2 C.1000×1 D.7.2÷1000
5.做一套校服需要1.9m布,20m最多可做( )套这样的校服。
A.10 B.11 C.12
6.李阿姨买了14个橘子共重2.1千克,如果买这样的橘子11千克,大约( )个。
A.不到50个 B.100个以上 C.70多个 D.不到60个
二、填空题
7.10.6÷6的商用循环小数表示是( ),保留两位小数是( )。
8.被除数扩大到原来的6倍,除数扩大到原来的3倍,商( )倍。
9.完成下表,电价按每千瓦时0.48元计算(得数保留两位小数)。
名称 每时耗电 量/千瓦时 每日耗电量/千瓦时 (按24小时计算) 每年耗电量/千瓦时 (按365天算) 每年所交电费/元 (按365天算)
冰箱 普通型 0.04 ( ) ( ) ( )
节能型 0.02 ( ) ( ) ( )
10.做一个水桶需要铁皮3.4m2,22.8m2的铁皮最多能做( )个水桶。
11.计算下面各题,说说你发现了什么?
0.32÷0.8=( ) 8÷0.4=( )
5.2÷1=( ) 3.67÷1=( )
80÷1.6=( ) 7.2÷1.2=( )
我发现:在小数除法的算式中,当除数大于1时,商( )被除数;当除数小于1时,商( )被除数。
12.循环小数0.ABCABC…的小数部分前60位上的数字和是100,这个循环小数的循环节是( )时这个循环小数最大,是( )时这个循环小数最小。(A、B、C为三个不同的自然数)
13.要使□.24÷6的商大于1,方框里可填( );如果商小于1,方框里可填( )。
14.贝贝心里想了一个数,于是她把这个数与它自己相加、相减、相除,所得的和、差、商加起来是10.6。贝贝心里想的数是( )。
三、解答题
15.一个没有拧紧的水龙头每天大约滴水1.8千克,请计算:
(1)一年(按365 天计算)浪费多少千克水?
(2)把这些水分装在饮水桶中(每桶水约重15千克),大约能装多少桶?
16.王乐在计算6.4除以一个数时,由于商的小数点向右点错了一位,结果是40,这道题的除数是多少?
17.校办工厂原来有3台制钉机,每小时可以制钉24.3千克.现在又增加了同样的制钉机2台,每小时一共可以制钉多少千克
18.甲、乙两袋大米的总质量是26.8千克,如果从甲袋中取出3.2千克放入乙袋,这时两袋大米的质量相等,原来甲、乙两袋大米各重多少千克?
19.同学们去爬枫叶山。已知同学们上山平均速度是每小时1.5千米,上山用了3小时;沿原路下山,下山用时2小时。那么同学们上山和下山的平均速度是多少?
20.看图解答。
参考答案:
1.A
【分析】根据题意可知,9=18÷2;4.5=9÷2,2.25=4.5÷2,…,由此可知,后一个数是前一个数的一半,用前一个数除以2,即可求出后一个数,据此解答。
【详解】1.125÷2=0.5625
按规律填数:18,9,4.5,2.25,1.125,0.5625,0.28125,…
故答案为:A
【点睛】解答本题的关键是根据已知的数得出前后数之间的变化规律,再利用变化规律进行解答。
2.A
【分析】根据题意,结合小数除法的计算法则可知,当4□.38的整数部分小于45时,4□.38÷45的商小于1。据此解题。
【详解】要使4□.38÷45的商小于1,□里应填小于5的数,即:0、1、2、3、4。
故答案为:A
【点睛】本题考查了小数除法,掌握小数除法的计算法则是解题的关键。
3.A
【分析】根据除法的意义,用45除以3.7即可求出共可以截成几段;用每段绳子的长度乘段数即可求出截去多少米,再用绳子的总长度减去截去的长度即可求出还剩下多少米。
【详解】45÷3.7≈12(段)
45-12×3.7
=45-44.4
=0.6(米)
则45米长的绳子,每3.7米截成一段,结果是12段余0.6米。
故答案为:A
【点睛】本题考查小数除法,明确小数除法的计算方法是解题的关键。
4.A
【分析】由于1欧元兑换人民币7.2元,则看1000元人民币里面有多少个7.2,有多少个7.2就能兑换多少个欧元,即1000÷7.2,由此即可选择。
【详解】由分析可知:1000÷7.2≈138.89(欧元)
故答案为:A。
【点睛】此题主要考查人民币的兑换方法,同时熟练掌握除法的意义是解题的关键。
5.A
【分析】求20米布可以做多少套校服,就是求20米里面有几个1.9米,用20除以1.9即可求解。
【详解】20÷1.9≈10(套)
故答案为:A
【点睛】解答此题应根据求一个数里面含有几个另一个数,用除法解答;注意:应结合实际情况,用“去尾”法。
6.C
【分析】14个橘子共2.1千克,用2.1千克除以14个,求出每个橘子的质量,再用11千克除以每个橘子的质量,即可求出11千克橘子的个数。
【详解】11÷(2.1÷14)
=11÷0.15
≈73(个)
买这样的橘子11千克,大约有70多个。
故答案为:C
【点睛】解决本题先根据除法平均分的意义求出每个橘子的质量,再根据除法的包含意义求解。
7. 1.77
【分析】计算出10.6÷6的商,找出循环节;根据循环小数的简写方法:在循环节的首位和末位的上面各记一个小圆点即可;将此数保留两位小数,就是精确到百分位,看千分位上的数,再运用“四舍五入”的方法求出近似数即可;据此进行解答。
【详解】10.6÷6=1.766……
1.766……=
≈1.77
【点睛】本题考查循环小数的简写,以及小数的近似数的求法。
8.扩大到原来的2
【分析】除数不变,被除数扩大几倍或缩小到原来的几分之一,商也同样扩大几倍或缩小到原来的几分之一;被除数不变,除数扩大几倍或缩小到原来的几分之一(0除外),商反而缩小到原来的几分之一或扩大相同的倍数。所以被除数扩大到原来的6倍,除数扩大到原来的3倍,商先扩大到原来的6倍,再缩小,也就是将商扩大到原来的(6÷3)倍。
【详解】6÷3=2
被除数扩大到原来的6倍,除数扩大到原来的3倍,商扩大到原来的2倍。
【点睛】掌握商的变化规律是解答本题的关键。
9.见详解
【分析】普通型冰箱:用普通型冰箱每小时耗电量×24小时,求出每日的耗电量;
再用每日的耗电量×365天,求出每年的耗电量;
再用每年耗电量×每千瓦时0.48元,即可求出普通型冰箱每年所交电费的钱数;
节能型冰箱:用节能型冰箱每小时耗电量×24小时,求出每日的耗电量;
再用每日的耗电量×365天,求出每年的耗电量;
再用每年耗电量×每千瓦时0.48元,即可求出节能型冰箱每年所交电费的钱数;
保留几位小数,就看保留小数的下一位小数,再根据“四舍五入”法进行解答。
【详解】普通型冰箱:0.04×24=0.96(千瓦时)
0.96×365=350.4(千瓦时)
350.4×0.48≈168.19(元)
节能型冰箱:0.02×24=0.48(千瓦时)
0.48×365=175.2(千瓦时)
175.2×0.48≈84.10(元)
名称 每时耗电 量/千瓦时 每日耗电量/千瓦时 (按24小时计算) 每年耗电量/千瓦时 (按365天算) 每年所交电费/元 (按365天算)
冰箱 普通型 0.04 0.96 350.4 168.19
节能型 0.02 0.48 175.2 84.10
【点睛】本题考查小数与整数的乘法计算,小数与小数的乘法计算,以及“四舍五入”法的应用。
10.6
【分析】根据题意,做一个水桶需要铁皮3.4m2,求22.8m2铁皮最多能做多少个水桶,就是求22.8里有多少个3.4,用除法计算,结果用去尾法保留整数。
【详解】22.8÷3.4≈6(个)
做一个水桶需要铁皮3.4m2,22.8m2的铁皮最多能做6个水桶。
【点睛】本题考查除数是小数的除法,注意结果用“去尾法”解答。
11. 0.4 20 5.2 3.67 50 6 小于 大于
【分析】计算小数除法时,先移动除数的小数点使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数末尾添0补足),然后按照除数是整数的小数除法进行计算;
先根据小数除法计算的方法求出各个题目的商,再观察算式中除数与1的大小关系,以及被除数与商的大小关系,从而找出规律。
【详解】由分析可得:
0.32÷0.8=0.4 8÷0.4=20
5.2÷1=5.2 3.67÷1=3.67
80÷1.6=50 7.2÷1.2=6
观察算式,可以发现:
一个数(0除外),除以大于1的数,商小于这个数;
一个数(0除外),除以等于1的数,商等于这个数;
一个数(0除外),除以小于1的数,商大于这个数;
综上所述:在小数除法的算式中,当除数大于1时,商小于被除数;当除数小于1时,商大于被除数。
【点睛】本题考查了小数除法的应用,要求熟悉被除数和除数以及商之间的关系,并且了解它们之间的变化规律。
12. 410 023
【分析】根据题意,这个循环小数的循环节是ABC,又因为小数部分前60位上的数字和是100,所以60÷3×(A+B+C)=100,由此可得A+B+C的数值,因为A、B、C为三个不同的自然数,可以列举出三个字母各自代替的数字,据此答题即可。
【详解】由分析可得:
60÷3×(A+B+C)=100
60÷3×(A+B+C)×3=100×3
60×(A+B+C)=300
A+B+C=300÷60
A+B+C=5
因为A、B、C为三个不同的自然数,所以这三个数只能分别是0、2、3或0、1、4,要想循环小数最大,让A最大,B第二大,C最小,即A=4,B=1,C=0,此时该循环小数为0.410410…,要想循环小数最小,则A最小,B第二小,C最大,即A=0,B=2,C=3,此时该循环小数为0.023023…。
综上所述:循环小数0.ABCABC…的小数部分前60位上的数字和是100,这个循环小数的循环节是410时这个循环小数最大,是023时这个循环小数最小。
【点睛】本题主要考查简单周期现象中的规律问题,关键是利用循环小数的特点做题。
13. 6,7,8,9 0,1,2,3,4,5
【分析】根据题意可知,除数是6,要使商大于1,□内的数大于或等于6;如果商小于1,□内的数小于6,据此解答。
【详解】□.24÷6的商大于1,□内可以填:6,7,8,9;
□.24÷6的商小于1,□内可以填:0,1,2,3,4,5。
要使□.24÷6的商大于1,方框里可填7,8,9;如果商小于1,方框里可填0,1,2,3,4,5。
【点睛】明确被除数与除数之间大小关系是解答本题的关键。
14.4.8
【分析】设这个数为x,相加为2x,相减为0,相除为1;2x加1等于10.6,由此列方程为2x+1=10.6,解方程即可。
【详解】解:设这个数为x,根据题意可得:
2x+(x-x)+x÷x=10.6
2x+1=10.6
2x=9.6
2x÷2=9.6÷2
x=4.8
贝贝心里想的数是4.8。
【点睛】解答此题的关键是理解和、差、商的意义,明确:两个相同的数差为0、商为1。
15.(1)657千克(2)44桶
【详解】(1)1.8×365=657(千克)
答:一年浪费657千克水
(2)657÷15=43.8(桶)≈44(桶)
答:大约能装44桶水
16.1.6
【详解】6.4÷4=1.6;
答:这道题的除数是1.6.
【点睛】因为商的小数点向右点错了一位,即商扩大了10倍,结果是40,正确的商应为4,求被除数,根据“被除数÷除数=商”进行解答即可.
17.40.5千克
【详解】解法1:
24.3÷3×(3+2)
=24.3÷3×5
=8.1×5
=40.5(千克)
解法2:24.3+24.3÷3×2
=24.3+8.1×2
=24.3+16.2
=40.5(千克)
答:每小时一共可以制钉40.5千克.
【点睛】解法1:先求出每台制钉机每小时制钉的重量,然后用每台制钉机每小时制钉的重量乘现在制钉机的台数即可求出现在每小时一共可以制钉的重量;解法2:用每台制钉机每小时制钉的重量乘2,再加上原来3台制钉的总重量就是现在一共可以制钉的重量.
18.甲: 16.6千克;乙:10.2千克
【详解】26.8÷2=13.4(千克) 甲:13.4+3.2=16.6(千克)
乙:13.4-3.2=10.2(千克)
19.1.8千米/小时
【分析】根据速度×时间=路程,把数代入公式即可求出上山的路程:1.5×3=4.5(千米),由于同学们上山和下山总共走了4.5×2=9(千米),用时:3+2=5(小时),根据公式:速度=路程÷时间,把数代入公式即可求解。
【详解】1.5×3×2÷(3+2)
=4.5×2÷5
=9÷5
=1.8(千米/时)
答:同学们上山和下山的平均速度是1.8千米/时。
【点睛】本题主要考查行程问题的公式,熟练掌握它的公式并灵活运用,求出往返的路程和时间是解题的关键。
20.见详解
【分析】根据单价×数量=总价,据此分别求出酱油、牛肉、鱼的总价;用实收的钱数减去找回的钱数即可求出应收的钱数,再用应收的钱数减去蛋糕、酱油、牛肉和鱼的总价,即可求出牛奶的总价,再根据总价÷数量=单价,据此求出牛奶的单价;。
【详解】(元)
(元)
(元)
(元)
(元)
24.5÷1=24.5(元)
如图所示:
【点睛】本题考查小数乘法,明确总价、数量和单价之间的关系是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
