思维拓展:小数除法(试题)数学五年级上册人教版(含答案)
文档属性
| 名称 | 思维拓展:小数除法(试题)数学五年级上册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 23:04:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
思维拓展:小数除法(试题)数学五年级上册人教版
一、选择题
1.下列算式中,a都是大于0而小于1的数,得数一定大于1的是( )。
A.a÷a B.a+a C.a×a D.1÷a
2.下面的算式中与结果不相等的算式是( )。
A. B. C. D.
3.小明家与奶奶家相距58.5km,爸爸开车去奶奶家,每分行1.5km,( )分可以到达奶奶家。
A.32 B.39 C.43
4.小明在计算一个数乘0.5时,把乘号看成了除号,结果是14,正确的结果是( )
A.28 B.3.5 C.14.5
5.如果甲×0.1=乙÷0.1(甲、乙都不为0),那么甲、乙两数之间的关系是( )。
A.甲>乙 B.甲<乙 C.甲=乙 D.无法确定
6.已知a=,b=,那么a÷b=( )。
A.2.4 B.24 C.0.24
二、填空题
7.根据172÷43=4,在括号里填上合适的数。
1720÷( )=4 ( )÷0.43=4
17.2÷4.3=( ) 0.172÷0.043=( )
172÷0.43=( ) 1.72÷4.3=( )
8.一个小数,把它的小数点向左移动两位后再除以原数,商是( )。
9.不计算,用发现的规律填空:
1.08÷0.9=1.2,
11.07÷0.9=12.3,
111.06÷0.9=123.4,
1111.05÷0.9= ,
÷0.9=12345.6。
10.两个数相除的商是2.4,如果被除数扩大到原来的100倍,除数除以0.01,商是( );A除以B的商是0.7余0.03。若A、B两数同时乘10,则其商是( ),余数是( )。
11.陈老师7.2分跑完1.44km,平均每分跑( )km,平均跑1km要用( )分。
12.某日银行,100泰铢可以兑换人民币19.36元。一个纪念品的标价是25泰铢,折合人民币( )元。
13.一个循环小数0.abab…(a,b都是非0自然数),这个数的小数部分前10位上的数字和是50,这个循环小数最大是( ),最小是( )。
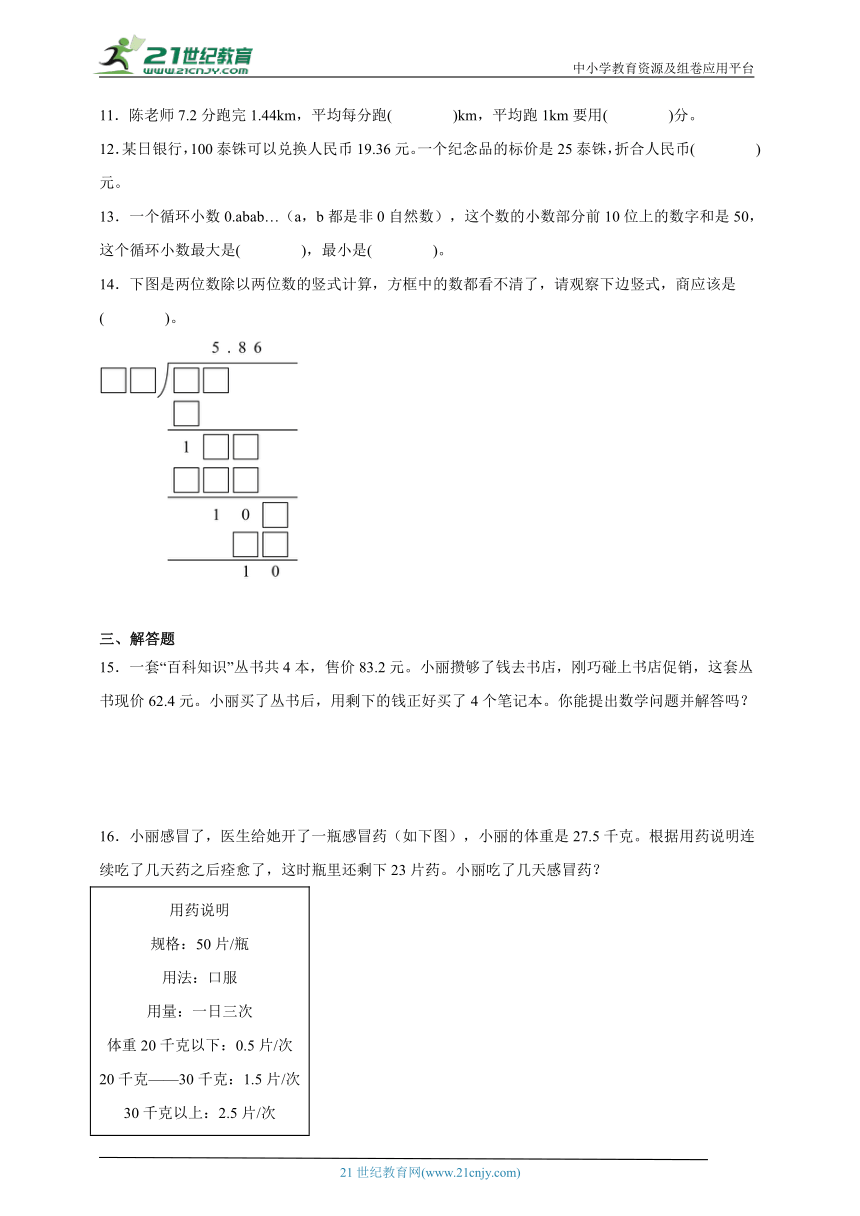
14.下图是两位数除以两位数的竖式计算,方框中的数都看不清了,请观察下边竖式,商应该是( )。
三、解答题
15.一套“百科知识”丛书共4本,售价83.2元。小丽攒够了钱去书店,刚巧碰上书店促销,这套丛书现价62.4元。小丽买了丛书后,用剩下的钱正好买了4个笔记本。你能提出数学问题并解答吗?
16.小丽感冒了,医生给她开了一瓶感冒药(如下图),小丽的体重是27.5千克。根据用药说明连续吃了几天药之后痊愈了,这时瓶里还剩下23片药。小丽吃了几天感冒药?
用药说明 规格:50片/瓶 用法:口服 用量:一日三次 体重20千克以下:0.5片/次 20千克——30千克:1.5片/次 30千克以上:2.5片/次
17.星星儿童制衣厂原来做一套童装需要1.8米布料,后来改进了裁剪方法,每套童装节约0.2米布料。原来准备做360套童装的布料,现在可以做多少套?
18.科学研究表明,10000平方米的森林每周可吸收6.3吨二氧化碳。城北的森林公园有50000平方米森林,今年8月份这片森林一共吸收了多少二氧化碳?
19.一个停车场停车1小时内收费8元,如果超过1小时,每多停半小时要多交2.5元(不足半小时按半小时计算)。
①李司机的车停了3.2小时,应付停车费多少元?
②王司机交了33元停车费。他的车最多停了多久?
20.疫情防控期间,第一实验小学每天给教室消毒需要使用4.6千克消毒液。
(1)每千克消毒液6.8元,学校每天使用的消毒液需要多少元钱?
(2)为了方便各班级使用,后勤处的陈老师每次都要把这些消毒液分装到小瓶中。每个小瓶最多能装0.5千克,陈老师至少需要准备多少个这样的小瓶?
参考答案:
1.D
【分析】如果a是大于0而小于1的数,可以设a为0.5,求出每个式子的值和1比较。
【详解】设a为0.5,则:
A.a÷a
=0.5÷0.5
=1;
B.a+a
=0.5+0.5
=1;
C.a×a
=0.5×0.5
=0.25;
D.1÷a
=1÷0.5
=2
四个选项中只有D选项得数大于1。
故选:D
【点睛】本题主要考查小数乘除法的应用,解答此题关键是通过计算,所得到的商大于这个数,然后再进一步解答即可。
2.C
【分析】根据商不变的规律:被除数和除数同时乘或除以一个不为0的数,商不变。据此解答即可。
【详解】A.,被除数乘10,除数也乘10,符合商不变的规律,与原式结果相等。
B.,被除数乘100,除数也乘100,符合商不变的规律,与原式结果相等。
C.,被除数除以10,除数乘10,不符合商不变的规律,与原式结果不相等。
D.,被除数除以10,除数也除以10,符合商不变的规律,与原式结果相等。
故选:C
【点睛】本题考查商不变的规律,灵活运用是解题的关键。
3.B
【分析】根据路程÷速度=时间,列式计算,根据小数除法的计算方法计算出结果即可。
【详解】58.5÷1.5=39(分)
39分可以到达奶奶家。
故答案为:B
【点睛】关键是理解速度、时间、路程之间的关系。
4.B
【分析】根据题意,一个数除以0.5得出结果是14,根据商×除数=被除数,可以用14×0.5就可以求出这个数,然后再用这个数去乘0.5即可求出正确的结果.
【详解】这个数是:14×0.5=7;
那么正确的结果是:7×0.5=3.5.
故选B.
5.A
【分析】假设甲×0.1=乙÷0.1=1,根据因数=积÷另一个因数,被除数=商×除数;据此解答。
【详解】假设甲×0.1=乙÷0.1=1
甲:1÷0.1=10
乙:1×0.1=0.1
0.1<10
所以甲>乙
故答案为:A
【点睛】本题可假设结果为1,然后求出甲和乙的值是解题的关键。
6.A
【分析】被除数和除数同时扩大几倍或缩小到原来的几分之一(0除外),商不变。小数点位置移动引起数的大小变化规律:一个数的小数点向右移动一位、两位、三位……,这个数就扩大到原来的10倍、100倍、1000倍……;是一个2006位小数,是也一个2007位小数;将和的小数点向右移动2006位,则变为6÷2.5,商不变,据此解答。
【详解】
所以a÷b=2.4
故答案为:A
【点睛】本题考查了除数是小数的小数除法以及小数点的移动规律。
7. 430 1.72 4 4 400 0.4
【分析】商的变化规律:
(1)除数不变,被除数扩大到原来的几倍,商也扩大到原来的几倍;除数不变,被除数缩小为原来的几分之一,商也缩小为原来的几分之一。
(2)被除数不变,除数扩大到原来的几倍,商反而缩小为原来的几分之一;被除数不变,除数缩小为原来的几分之一,商反而扩大到原来的几倍。
(3)被除数和除数同时乘或除以相同的不为0的数,商不变。
【详解】根据172÷43=4,可得:
1720÷430=4 1.72÷0.43=4
17.2÷4.3=4 0.172÷0.043=4
172÷0.43=400 1.72÷4.3=0.4
【点睛】关键是掌握并灵活运用商的变化规律。
8.0.01
【分析】可假定这个数是1.2,把它的小数点向左移动两位,那么这个数就是0.012,用0.012除以1.2 求出商即可。
【详解】假定这个数是1.2,则:
0.012÷1.2=0.01
【点睛】解决本题利用赋值法比较简单,设出数据,求出移动小数点后形成的数,进而求解。
9. 1234.5 11111.04
【分析】观察已给的式子,除数都是0.9,被除数的整数部分有几个1,商的整数部分就有几位,商的小数部分只有一位,商从自然数1开始每个数字比前一个数字大1,被除数的小数部分第一个数字是0,第二个数字与商的小数部分的数加起来是10。
【详解】1111.05÷0.9=1234.5,11111.04÷0.9=12345.6。
【点睛】此题考查学生的观察推理能力,找到算式的规律是解题的关键。
10. 2.4 0.7 0.3
【分析】(1)除数除以0.01,相当于除数扩大到原来的100倍,被除数和除数同时扩大到原来的100倍,商不变;
(2)被除数和除数同时乘10,商不变,余数的小数点和被除数移动后的小数点位置一致,据此解答。
【详解】两个数相除的商是2.4,如果被除数扩大到原来的100倍,除数除以0.01,商是( 2.4 );A除以B的商是0.7余0.03。若A、B两数同时乘10,则其商是( 2.4 ),余数是( 0.3 )。
【点睛】掌握商的变化规律是解答题目的关键。
11. 0.2 5
【分析】已知陈老师7.2分跑完1.44km,求平均每分跑多少km,就是求陈老师跑步的速度,根据“速度=路程÷时间”,代入数据计算求解;
求平均跑1km要用多少时间,根据“时间=路程÷速度”,代入数据计算求解。
【详解】1.44÷7.2=0.2(km)
1÷0.2=5(分)
平均每分跑0.2 km,平均跑1km要用5分。
【点睛】本题考查小数除法的应用,掌握速度、时间、路程之间的关系是解题的关键。
12.4.84
【分析】已知100泰铢可以兑换人民币19.36元,先用除法求出1泰铢可以兑换人民币多少元,再乘25,即是25泰铢折合人民币的钱数。
【详解】19.36÷100×25
=0.1936×25
=4.84(元)
折合人民币4.84元。
【点睛】本题考查小数乘除法的应用,掌握外汇与人民币的换算方法是解题的关键。
13. 0.919191… 0.191919…
【分析】这个数小数部分前10位上的数字和是50,即5(A+B)=50,则A+B=10,据此解答。
【详解】由题意可知:
5(A+B)=50
A+B=10
所以这个循环小数最大是0.919191…,最小是0.191919…。
【点睛】解答此题的关键是:先根据题意,求出A+B的和,然后根据要使循环小数最大,十分位应最大,为9,百分位为1;反之,要使循环小数最大,十分位应最小,为1,百分位为9。
14./5.8666…
【分析】根据除数是两位数的除法的计算方法可知100个百分之一除以两位数商6,余数是10,那么继续除下去,在被除数末尾添0,100个千分之一除以两位数商仍是6,余数仍是10,据此解答。
【详解】从竖式可知,100个百分之一除以两位数后商6余数是10,继续除,则100个千分之一除以两位数后商仍然是6余数是10,以此类推,商应该是。
【点睛】考查循环小数的认识和简写。
15.每本笔记本多少钱?5.2元
【分析】提问如:每本笔记本多少钱?(原来的售价-现价)÷笔记本数量=笔记本单价,据此列式解答。
【详解】每本笔记本多少钱?
(83.2-62.4)÷4
=20.8÷4
=5.2(元)
答:每本笔记本5.2元钱。
(答案不唯一)
【点睛】关键是根据已知条件提出合理的问题,掌握小数除法的计算方法。
16.6天
【分析】根据题意可知,小丽的体重是27.5千克,则小丽需要每次吃1.5片;已知一瓶有50片,还剩下23片药,则说明小丽吃了(50-23)片;一日3次,则小丽每天吃(3×1.5)片,然后用(50-23)÷(3×1.5)即可求出吃药的天数。
【详解】30>27.5>20
小丽需要每次吃1.5片;
(50-23)÷(3×1.5)
=27÷4.5
=6(天)
答:小丽吃了6天感冒药。
【点睛】本题考查了小数除法的计算和应用,掌握相应的计算方法是解答本题的关键。
17.405套
【分析】利用减法,求出现在做一套童装需要多少米的布料。将原来每套衣服的布料乘360套,求出布料一共有多少米,再将其除以现在每套衣服需要的布料1.6米,求出现在可以做多少套。
【详解】1.8×360÷(1.8-0.2)
=648÷1.6
=405(套)
答:现在可以做405套。
【点睛】本题考查了小数乘除法应用题,求出布料总长是解题的关键。
18.139.5吨
【分析】先用6.3÷7÷10000求出1平方米森林平均每天吸收二氧化碳的吨数;再用1平方米森林平均每天吸收二氧化碳的吨数×50000×31,求出50000平方米森林8月份(31天)吸收二氧化碳的吨数。
【详解】1周有7天,8月份有31天。
6.3÷7÷10000×50000×31
=0.00009×50000×31
=139.5(吨)
答:今年8月份这片森林一共吸收了139.5二氧化碳。
【点睛】此题考查了小数乘、除法的计算方法及归一问题。
19.①20.5元
②6小时
【分析】①李司机的车停了3.2小时,按3.5小时收费,先求出超出1小时的部分,除以0.5,求出超出几个半小时,乘对应收费标准,再加上1小时内的费用即可。
②先减去1小时内的费用,除以2.5,求出超出几个半小时,超出的半小时数×0.5+1=最多停车时间。
【详解】①3.2小时按3.5小时收费。
(3.5-1)÷0.5×2.5+8
=2.5÷0.5×2.5+8
=12.5+8
=20.5(元)
答:应付停车费20.5元。
②(33-8)÷2.5×0.5+1
=25÷2.5×0.5+1
=5+1
=6(小时)
答:他的车最多停了6小时。
【点睛】关键是理解收费规则,掌握小数乘除法的计算方法。
20.(1)31.28元
(2)10个
【分析】(1)已知每千克消毒液6.8元,学校每天使用4.6千克消毒液,根据“总价=单价×数量”,代入数据计算,即可求出学校每天使用消毒液需要的钱数。
(2)求分装4.6千克消毒液至少需要多少个0.5千克的小瓶,也就是求4.6千克里面有几个0.5千克,用除法计算,得数采用“进一法”取整数。
【详解】(1)6.8×4.6=31.28(元)
答:学校每天使用的消毒液需要31.28元。
(2)4.6÷0.5≈10(个)
答:陈老师至少需要准备10个这样的小瓶。
【点睛】(1)本题考查小数乘法的意义及应用,掌握单价、数量、总价之间的关系是解题的关键。
(2)本题考查小数除法的意义及应用,注意计算结果要结合生活实际,采用“进一法”取近似数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:小数除法(试题)数学五年级上册人教版
一、选择题
1.下列算式中,a都是大于0而小于1的数,得数一定大于1的是( )。
A.a÷a B.a+a C.a×a D.1÷a
2.下面的算式中与结果不相等的算式是( )。
A. B. C. D.
3.小明家与奶奶家相距58.5km,爸爸开车去奶奶家,每分行1.5km,( )分可以到达奶奶家。
A.32 B.39 C.43
4.小明在计算一个数乘0.5时,把乘号看成了除号,结果是14,正确的结果是( )
A.28 B.3.5 C.14.5
5.如果甲×0.1=乙÷0.1(甲、乙都不为0),那么甲、乙两数之间的关系是( )。
A.甲>乙 B.甲<乙 C.甲=乙 D.无法确定
6.已知a=,b=,那么a÷b=( )。
A.2.4 B.24 C.0.24
二、填空题
7.根据172÷43=4,在括号里填上合适的数。
1720÷( )=4 ( )÷0.43=4
17.2÷4.3=( ) 0.172÷0.043=( )
172÷0.43=( ) 1.72÷4.3=( )
8.一个小数,把它的小数点向左移动两位后再除以原数,商是( )。
9.不计算,用发现的规律填空:
1.08÷0.9=1.2,
11.07÷0.9=12.3,
111.06÷0.9=123.4,
1111.05÷0.9= ,
÷0.9=12345.6。
10.两个数相除的商是2.4,如果被除数扩大到原来的100倍,除数除以0.01,商是( );A除以B的商是0.7余0.03。若A、B两数同时乘10,则其商是( ),余数是( )。
11.陈老师7.2分跑完1.44km,平均每分跑( )km,平均跑1km要用( )分。
12.某日银行,100泰铢可以兑换人民币19.36元。一个纪念品的标价是25泰铢,折合人民币( )元。
13.一个循环小数0.abab…(a,b都是非0自然数),这个数的小数部分前10位上的数字和是50,这个循环小数最大是( ),最小是( )。
14.下图是两位数除以两位数的竖式计算,方框中的数都看不清了,请观察下边竖式,商应该是( )。
三、解答题
15.一套“百科知识”丛书共4本,售价83.2元。小丽攒够了钱去书店,刚巧碰上书店促销,这套丛书现价62.4元。小丽买了丛书后,用剩下的钱正好买了4个笔记本。你能提出数学问题并解答吗?
16.小丽感冒了,医生给她开了一瓶感冒药(如下图),小丽的体重是27.5千克。根据用药说明连续吃了几天药之后痊愈了,这时瓶里还剩下23片药。小丽吃了几天感冒药?
用药说明 规格:50片/瓶 用法:口服 用量:一日三次 体重20千克以下:0.5片/次 20千克——30千克:1.5片/次 30千克以上:2.5片/次
17.星星儿童制衣厂原来做一套童装需要1.8米布料,后来改进了裁剪方法,每套童装节约0.2米布料。原来准备做360套童装的布料,现在可以做多少套?
18.科学研究表明,10000平方米的森林每周可吸收6.3吨二氧化碳。城北的森林公园有50000平方米森林,今年8月份这片森林一共吸收了多少二氧化碳?
19.一个停车场停车1小时内收费8元,如果超过1小时,每多停半小时要多交2.5元(不足半小时按半小时计算)。
①李司机的车停了3.2小时,应付停车费多少元?
②王司机交了33元停车费。他的车最多停了多久?
20.疫情防控期间,第一实验小学每天给教室消毒需要使用4.6千克消毒液。
(1)每千克消毒液6.8元,学校每天使用的消毒液需要多少元钱?
(2)为了方便各班级使用,后勤处的陈老师每次都要把这些消毒液分装到小瓶中。每个小瓶最多能装0.5千克,陈老师至少需要准备多少个这样的小瓶?
参考答案:
1.D
【分析】如果a是大于0而小于1的数,可以设a为0.5,求出每个式子的值和1比较。
【详解】设a为0.5,则:
A.a÷a
=0.5÷0.5
=1;
B.a+a
=0.5+0.5
=1;
C.a×a
=0.5×0.5
=0.25;
D.1÷a
=1÷0.5
=2
四个选项中只有D选项得数大于1。
故选:D
【点睛】本题主要考查小数乘除法的应用,解答此题关键是通过计算,所得到的商大于这个数,然后再进一步解答即可。
2.C
【分析】根据商不变的规律:被除数和除数同时乘或除以一个不为0的数,商不变。据此解答即可。
【详解】A.,被除数乘10,除数也乘10,符合商不变的规律,与原式结果相等。
B.,被除数乘100,除数也乘100,符合商不变的规律,与原式结果相等。
C.,被除数除以10,除数乘10,不符合商不变的规律,与原式结果不相等。
D.,被除数除以10,除数也除以10,符合商不变的规律,与原式结果相等。
故选:C
【点睛】本题考查商不变的规律,灵活运用是解题的关键。
3.B
【分析】根据路程÷速度=时间,列式计算,根据小数除法的计算方法计算出结果即可。
【详解】58.5÷1.5=39(分)
39分可以到达奶奶家。
故答案为:B
【点睛】关键是理解速度、时间、路程之间的关系。
4.B
【分析】根据题意,一个数除以0.5得出结果是14,根据商×除数=被除数,可以用14×0.5就可以求出这个数,然后再用这个数去乘0.5即可求出正确的结果.
【详解】这个数是:14×0.5=7;
那么正确的结果是:7×0.5=3.5.
故选B.
5.A
【分析】假设甲×0.1=乙÷0.1=1,根据因数=积÷另一个因数,被除数=商×除数;据此解答。
【详解】假设甲×0.1=乙÷0.1=1
甲:1÷0.1=10
乙:1×0.1=0.1
0.1<10
所以甲>乙
故答案为:A
【点睛】本题可假设结果为1,然后求出甲和乙的值是解题的关键。
6.A
【分析】被除数和除数同时扩大几倍或缩小到原来的几分之一(0除外),商不变。小数点位置移动引起数的大小变化规律:一个数的小数点向右移动一位、两位、三位……,这个数就扩大到原来的10倍、100倍、1000倍……;是一个2006位小数,是也一个2007位小数;将和的小数点向右移动2006位,则变为6÷2.5,商不变,据此解答。
【详解】
所以a÷b=2.4
故答案为:A
【点睛】本题考查了除数是小数的小数除法以及小数点的移动规律。
7. 430 1.72 4 4 400 0.4
【分析】商的变化规律:
(1)除数不变,被除数扩大到原来的几倍,商也扩大到原来的几倍;除数不变,被除数缩小为原来的几分之一,商也缩小为原来的几分之一。
(2)被除数不变,除数扩大到原来的几倍,商反而缩小为原来的几分之一;被除数不变,除数缩小为原来的几分之一,商反而扩大到原来的几倍。
(3)被除数和除数同时乘或除以相同的不为0的数,商不变。
【详解】根据172÷43=4,可得:
1720÷430=4 1.72÷0.43=4
17.2÷4.3=4 0.172÷0.043=4
172÷0.43=400 1.72÷4.3=0.4
【点睛】关键是掌握并灵活运用商的变化规律。
8.0.01
【分析】可假定这个数是1.2,把它的小数点向左移动两位,那么这个数就是0.012,用0.012除以1.2 求出商即可。
【详解】假定这个数是1.2,则:
0.012÷1.2=0.01
【点睛】解决本题利用赋值法比较简单,设出数据,求出移动小数点后形成的数,进而求解。
9. 1234.5 11111.04
【分析】观察已给的式子,除数都是0.9,被除数的整数部分有几个1,商的整数部分就有几位,商的小数部分只有一位,商从自然数1开始每个数字比前一个数字大1,被除数的小数部分第一个数字是0,第二个数字与商的小数部分的数加起来是10。
【详解】1111.05÷0.9=1234.5,11111.04÷0.9=12345.6。
【点睛】此题考查学生的观察推理能力,找到算式的规律是解题的关键。
10. 2.4 0.7 0.3
【分析】(1)除数除以0.01,相当于除数扩大到原来的100倍,被除数和除数同时扩大到原来的100倍,商不变;
(2)被除数和除数同时乘10,商不变,余数的小数点和被除数移动后的小数点位置一致,据此解答。
【详解】两个数相除的商是2.4,如果被除数扩大到原来的100倍,除数除以0.01,商是( 2.4 );A除以B的商是0.7余0.03。若A、B两数同时乘10,则其商是( 2.4 ),余数是( 0.3 )。
【点睛】掌握商的变化规律是解答题目的关键。
11. 0.2 5
【分析】已知陈老师7.2分跑完1.44km,求平均每分跑多少km,就是求陈老师跑步的速度,根据“速度=路程÷时间”,代入数据计算求解;
求平均跑1km要用多少时间,根据“时间=路程÷速度”,代入数据计算求解。
【详解】1.44÷7.2=0.2(km)
1÷0.2=5(分)
平均每分跑0.2 km,平均跑1km要用5分。
【点睛】本题考查小数除法的应用,掌握速度、时间、路程之间的关系是解题的关键。
12.4.84
【分析】已知100泰铢可以兑换人民币19.36元,先用除法求出1泰铢可以兑换人民币多少元,再乘25,即是25泰铢折合人民币的钱数。
【详解】19.36÷100×25
=0.1936×25
=4.84(元)
折合人民币4.84元。
【点睛】本题考查小数乘除法的应用,掌握外汇与人民币的换算方法是解题的关键。
13. 0.919191… 0.191919…
【分析】这个数小数部分前10位上的数字和是50,即5(A+B)=50,则A+B=10,据此解答。
【详解】由题意可知:
5(A+B)=50
A+B=10
所以这个循环小数最大是0.919191…,最小是0.191919…。
【点睛】解答此题的关键是:先根据题意,求出A+B的和,然后根据要使循环小数最大,十分位应最大,为9,百分位为1;反之,要使循环小数最大,十分位应最小,为1,百分位为9。
14./5.8666…
【分析】根据除数是两位数的除法的计算方法可知100个百分之一除以两位数商6,余数是10,那么继续除下去,在被除数末尾添0,100个千分之一除以两位数商仍是6,余数仍是10,据此解答。
【详解】从竖式可知,100个百分之一除以两位数后商6余数是10,继续除,则100个千分之一除以两位数后商仍然是6余数是10,以此类推,商应该是。
【点睛】考查循环小数的认识和简写。
15.每本笔记本多少钱?5.2元
【分析】提问如:每本笔记本多少钱?(原来的售价-现价)÷笔记本数量=笔记本单价,据此列式解答。
【详解】每本笔记本多少钱?
(83.2-62.4)÷4
=20.8÷4
=5.2(元)
答:每本笔记本5.2元钱。
(答案不唯一)
【点睛】关键是根据已知条件提出合理的问题,掌握小数除法的计算方法。
16.6天
【分析】根据题意可知,小丽的体重是27.5千克,则小丽需要每次吃1.5片;已知一瓶有50片,还剩下23片药,则说明小丽吃了(50-23)片;一日3次,则小丽每天吃(3×1.5)片,然后用(50-23)÷(3×1.5)即可求出吃药的天数。
【详解】30>27.5>20
小丽需要每次吃1.5片;
(50-23)÷(3×1.5)
=27÷4.5
=6(天)
答:小丽吃了6天感冒药。
【点睛】本题考查了小数除法的计算和应用,掌握相应的计算方法是解答本题的关键。
17.405套
【分析】利用减法,求出现在做一套童装需要多少米的布料。将原来每套衣服的布料乘360套,求出布料一共有多少米,再将其除以现在每套衣服需要的布料1.6米,求出现在可以做多少套。
【详解】1.8×360÷(1.8-0.2)
=648÷1.6
=405(套)
答:现在可以做405套。
【点睛】本题考查了小数乘除法应用题,求出布料总长是解题的关键。
18.139.5吨
【分析】先用6.3÷7÷10000求出1平方米森林平均每天吸收二氧化碳的吨数;再用1平方米森林平均每天吸收二氧化碳的吨数×50000×31,求出50000平方米森林8月份(31天)吸收二氧化碳的吨数。
【详解】1周有7天,8月份有31天。
6.3÷7÷10000×50000×31
=0.00009×50000×31
=139.5(吨)
答:今年8月份这片森林一共吸收了139.5二氧化碳。
【点睛】此题考查了小数乘、除法的计算方法及归一问题。
19.①20.5元
②6小时
【分析】①李司机的车停了3.2小时,按3.5小时收费,先求出超出1小时的部分,除以0.5,求出超出几个半小时,乘对应收费标准,再加上1小时内的费用即可。
②先减去1小时内的费用,除以2.5,求出超出几个半小时,超出的半小时数×0.5+1=最多停车时间。
【详解】①3.2小时按3.5小时收费。
(3.5-1)÷0.5×2.5+8
=2.5÷0.5×2.5+8
=12.5+8
=20.5(元)
答:应付停车费20.5元。
②(33-8)÷2.5×0.5+1
=25÷2.5×0.5+1
=5+1
=6(小时)
答:他的车最多停了6小时。
【点睛】关键是理解收费规则,掌握小数乘除法的计算方法。
20.(1)31.28元
(2)10个
【分析】(1)已知每千克消毒液6.8元,学校每天使用4.6千克消毒液,根据“总价=单价×数量”,代入数据计算,即可求出学校每天使用消毒液需要的钱数。
(2)求分装4.6千克消毒液至少需要多少个0.5千克的小瓶,也就是求4.6千克里面有几个0.5千克,用除法计算,得数采用“进一法”取整数。
【详解】(1)6.8×4.6=31.28(元)
答:学校每天使用的消毒液需要31.28元。
(2)4.6÷0.5≈10(个)
答:陈老师至少需要准备10个这样的小瓶。
【点睛】(1)本题考查小数乘法的意义及应用,掌握单价、数量、总价之间的关系是解题的关键。
(2)本题考查小数除法的意义及应用,注意计算结果要结合生活实际,采用“进一法”取近似数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
