思维拓展:多边形的面积(试题)数学五年级上册苏教版(含答案)
文档属性
| 名称 | 思维拓展:多边形的面积(试题)数学五年级上册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 09:15:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
思维拓展:多边形的面积(试题)数学五年级上册苏教版
一、选择题
1.下图平行线间三个图形的面积相比较,( )。
A.三个图形的面积相等 B.三角形的面积最大
C.平行四边形的面积最小 D.梯形面积最大
2.如图ABCD为长方形,EFCD为平行四边形,比较阴影部分甲,乙的面积,( )。
A.甲大 B.乙大 C.甲乙一样大 D.无法确定
3.一个平行四边形的底是10厘米,高是6厘米。如果把它的底和高分别乘3,那么它的面积( )。
A.扩大3倍 B.扩大6倍 C.扩大9倍 D.无法确定
4.如图,梯形被分为平行四边形和三角形,三角形的面积是32平方厘米,梯形的面积是( )平方厘米。
A.32 B.64 C.96 D.128
5.如下图,阴影部分的面积是20平方厘米,那么平行四边形的面积是( )平方厘米。
A.20 B.30 C.40 D.50
6.一个长方形的长去掉4厘米后,面积就减少了20平方厘米,剩下的部分正好是一个正方形,原来的长方形的面积是( )平方厘米。
A.25 B.45 C.5 D.20
二、填空题
7.一个平行四边形的底是32厘米,高是2分米,它的面积是( )平方分米,和它等底等高的三角形的面积是( )平方分米。
8.一个直角三角形的两条直角边分别是3厘米、4厘米,这个直角三角形的面积是( )平方厘米.如果这个直角三角形的斜边长是5厘米,那么这条斜边上的高是( )厘米.
9.下图中的阴影部分的面积是( )平方厘米。
10.一个梯形的面积是28平方米,它的高是7米,上底是3米,下底是( )米;用两个这样的梯形拼成一个平行四边形,平行四边形的面积是( )。
11.一堆钢管堆成了横截面为梯形,最上层有2根,最下层有12根,相邻两层相差1根,这堆钢管一共有( )根。
12.如图,把平行四边形剪成一个三角形和一个梯形,那么三角形的面积是( )cm2,梯形的面积是( )cm2。
13.如图,把一个平行四边形框架拉成长方形,面积增加了。原来平行四边形的高是( )cm。
14.一块梯形田地,它的上下底之和是120米,高是30米,面积是( )平方米。
三、解答题
15.一个梯形下底是上底的3倍,如果把上底延长8厘米,就得到一个平行四边形,且面积增加24平方厘米,这个梯形面积是多少平方厘米?
16.一块直角梯形地,它的下底是40米,如果上底增加38米,这块地就变成了正方形.原来梯形的面积是多少
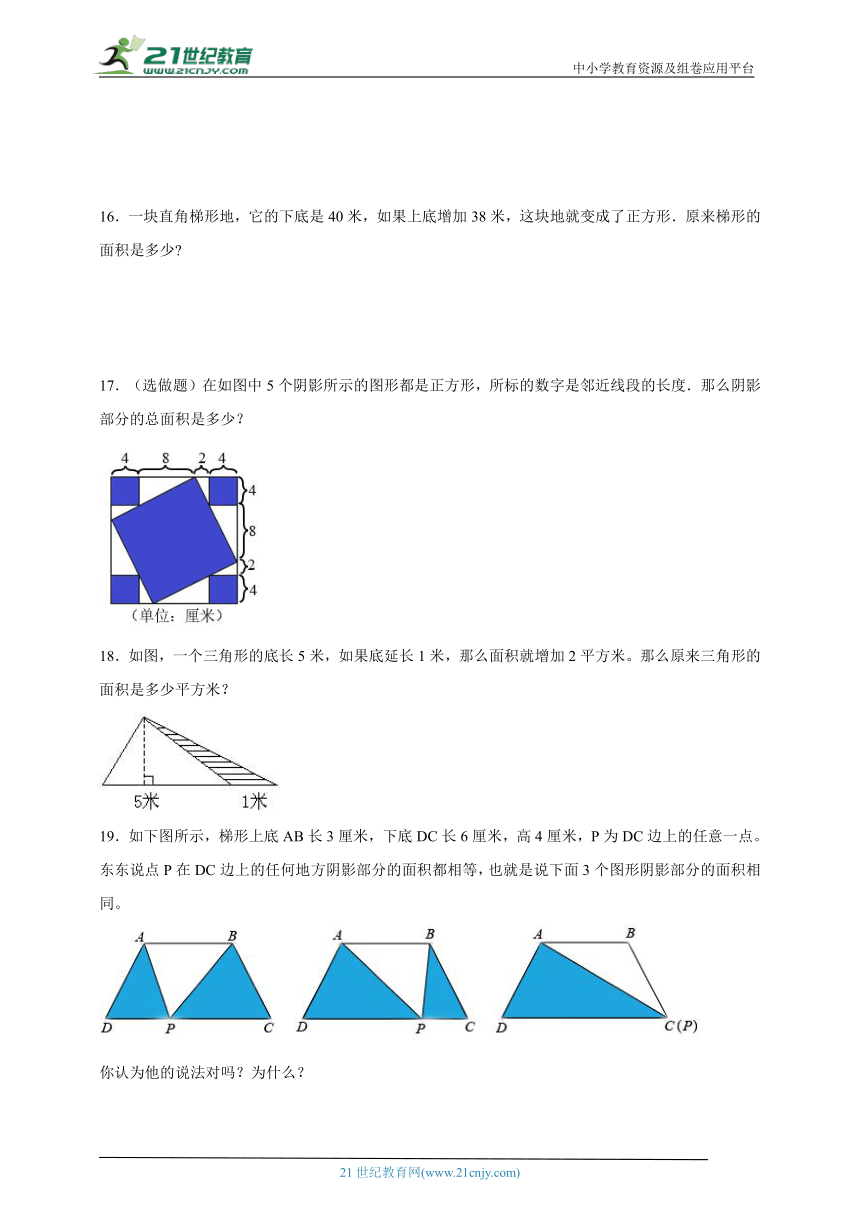
17.(选做题)在如图中5个阴影所示的图形都是正方形,所标的数字是邻近线段的长度.那么阴影部分的总面积是多少?
18.如图,一个三角形的底长5米,如果底延长1米,那么面积就增加2平方米。那么原来三角形的面积是多少平方米?
19.如下图所示,梯形上底AB长3厘米,下底DC长6厘米,高4厘米,P为DC边上的任意一点。东东说点P在DC边上的任何地方阴影部分的面积都相等,也就是说下面3个图形阴影部分的面积相同。
你认为他的说法对吗?为什么?
20.2022年11月29日,搭载神舟十五号载人飞船的长征二号F遥十五运载火箭在酒泉卫星发射中心点火发射,中国航天事业又取得了一个新成就。实验小学组织学生到航天科技馆参观,科技馆内有一架火箭模型的标志牌(如下图)。如果要粉刷标志牌的正、反两面,需要粉刷的面积有多少平方厘米?
参考答案:
1.A
【分析】由图可知:三个图形的高(长)相等,长方形的宽,梯形的上底、下底,三角形的底都已知,再依据三者的面积公式求出它们的面积,比较即可。
【详解】假设长方形的长、三角形的高、梯形的高均为h,
长方形的面积为:4×h=4h
三角形的面积:8×h÷2=4h
梯形的面积:(2+6)×h÷2=4h
所以三个图形的面积相等,
故答案为:A
【点睛】此题主要考查三角形、梯形、长方形的面积公式,牢记公式是解题的关键。
2.C
【详解】因为长方形ABCD的高与平行四边形EFCD的高相等,那么长方形ABCD与平行四边形EFCD的面积相等,同时减去三角形CDF的面积,所以甲、乙两部分面积是相等的。
所以答案为:C
3.C
【分析】平行四边形的面积公式:s=ah,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积。
【详解】因为平行四边形的面积=底×高,如果把它的底和高分别乘3,那么它的面积就扩大3×3=9倍。
故答案为:C
【点睛】此题主要根据平行四边形的面积公式以及因数与积的变化规律解决问题。
4.C
【分析】根据图可知,三角形的底和平行四边形的底是相同的,高也是相同的,根据平行四边形的面积公式:底×高;三角形的面积公式:底×高÷2,由此即可知道等底等高的平行四边形的面积是三角形面积的2倍,则平行四边形的面积是:32×2=64(平方厘米),再加上三角形的面积即可求出梯形的面积。
【详解】32×2+32
=64+32
=96(平方厘米)
所以梯形的面积是96平方厘米。
故答案为:C
【点睛】本题主要考查平行四边形和三角形的面积公式,熟练掌握它们的面积公式并灵活运用。
5.C
【分析】观察图形可知,阴影部分是两个三角形的和,两个三角形的底的和等于平行四边形的底,三角形的高等于平行四边形的高;根据三角形面积公式:面积=底×高÷2;平行四边形面积公式:面积=底×高;由此可知,阴影部分的面积等于平行四边形面积的一半;即平行四边形面积=三角形面积×2,据此求出平行四边形面积。
【详解】20×2=40(平方厘米)
如下图,阴影部分的面积是20平方厘米,那么平行四边形的面积是40平方厘米。
故答案为:C
【点睛】解答本题的关键明确阴影部分的底的和与平行四边形的底的关系,阴影部分的高与平行四边形的高之间的关系是解答本题的关键。
6.B
【分析】根据长方形的面积公式:S=ab,那么b=S÷a,用减少的面积除以减少的长求出原来的宽,因为剩下的部分正好是一个正方形,所以宽加上4厘米就是原来的长,再把数据代入公式求出原来的面积。
【详解】20÷4=5(厘米)
(5+4)×5
=9×5
=45(平方厘米)
故答案为:B
【点睛】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
7. 6.4 3.2
【分析】先把32厘米化为3.2分米,然后根据平行四边形的面积=底×高和三角形的面积=底×高÷2,代入数据解答即可。
【详解】32厘米=3.2分米
3.2×2=6.4(平方分米)
3.2×2÷2=3.2(平方分米)
平行四边形的面积是6.4平方分米,和它等底等高的三角形的面积是3.2平方分米。
【点睛】本题主要考查了平行四边形和三角形面积公式的灵活应用,要熟练掌握相关公式。
8. 6 2.4
【解析】略
9.120
【分析】三个三角形的底的和是20厘米,根据三角形的面积=底×高求出阴影部分的面积。
【详解】20×12÷2
=240÷2
=120(平方厘米)
【点睛】考查了三角形的面积,学生应灵活应用其公式。
10. 5 56平方米
【分析】由“梯形的面积=(上底+下底)×高÷2”可得“梯形的下底=梯形的面积×2÷高-上底”,梯形的上底、高和面积已知,代入此关系式即可求解;用梯形的面积×2即可;据此解答。
【详解】28×2÷7-3
=56÷7-3
=8-3
=5(米)
28×2=56(平方米)
【点睛】本题主要考查梯形面积公式的灵活应用,牢记梯形面积公式是解题的关键。
11.77
【分析】相邻两层相差1根,那么用最下层的12根减去最上层的2根再加1,可以求出这堆钢管有几层,再根据梯形的面积=(上底+下底)×高÷2,列式求出这堆钢管一共多少根。
【详解】12-2+1=11(层)
(12+2)×11÷2
=14×11÷2
=77(根)
所以,这堆钢管一共有77根。
【点睛】本题的关键是灵活运用梯形的面积公式,找准梯形的高。
12. 15 35
【分析】由图可知,三角形底为6厘米,高为5厘米,由三角形面积=底×高÷2,代入数据可得。因为平行四边形对边相等,所以梯形的下底=平行四边形的底=10厘米,梯形上底:10-6=4厘米,由梯形面积=(上底+下底)×高÷2,代入数据可得。
【详解】三角形面积:5×6÷2
=30÷2
=15(平方厘米);
梯形上底:10-6=4(厘米)
梯形面积:(4+10)×5÷2
=14×5÷2
=70÷2
=35(平方厘米)
【点睛】此题考查的是三角形面积与梯形面积公式,能熟练应用并找到平行四边形对边相等的隐含条件是解题的关键。
13.10
【分析】根据长方形面积公式:S=长×宽,代入数值求出该长方形的面积,用求出的长方形面积减去40,可求出原来平行四边形的面积;通过对图的观察,在把平行四边形框架拉成长方形的过程中,平行四边形的底没有变,其底就是长方形的底,改变的是平行四边形的高,利用平行四边形面积公式:S=底×高,将数据代入可以求出原平行四边形的高。
【详解】由分析可得:
(20×12-40)÷20
=(240-40)÷20
=200÷20
=10(cm)
综上所述:如图,把一个平行四边形框架拉成长方形,面积增加了。原来平行四边形的高是10cm。
【点睛】本题考查了长方形、平行四边形面积公式的灵活运用,熟记公式是解题的关键。
14.1800
【分析】根据梯形的面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】120×30÷2
=3600÷2
=1800(平方米)
这块梯形田地的面积是1800平方米。
【点睛】此题主要考查梯形面积的实际应用,熟练掌握其公式是解题关键。
15.48平方厘米
【分析】根据题意,设上底为x厘米,下底为3x厘米,已知如果把上底延长8厘米,就得到一个平行四边形,也就是上底+8=下底,以此列方程求出上底和下底,因为增加的面积是三角形面积,底是8厘米,根据三角形面积=底×高÷2求出高,也就是梯形的高,再根据梯形的面积=(上底+下底)×高÷2即可解答。
【详解】解:设上底为x厘米,下底为3x厘米。
x+8=3x
2x=8
x=4
下底:4×3=12(厘米)
高:24×2÷8
=48÷8
=6(厘米)
梯形面积:(4+12)×6÷2
=16×6÷2
=96÷2
=48(平方厘米)
答:这个梯形面积是48平方厘米。
【点睛】此题主要考查学生对三角形和梯形面积公式的灵活应用,以及可以用方程解答未知数。
16.840平方米
【详解】(40-38+40)×40÷2
=42×40÷2
=840(平方米)
答:原来梯形的面积是840平方米.
17.244平方厘米
【分析】用大正方形的面积减去四个两条直角边是8和4的直角三角形的面积,再减去4个两条直角边是4和2的直角三角形的面积。据此解答。
【详解】(4+8+2+4)×(4+8+2+4)
=18×18
=324(平方厘米)
大直角三角形的面积:
8×4÷2
=32÷2
=16(平方厘米)
小直角三角形的面积:
4×2÷2
=8÷2
=4(平方厘米),
324-16×4-4×4
=324-64-16
=244(平方厘米)
答:阴影部分的面积是244平方厘米。
【点睛】本题的关键是根据图形,用大正方形的面积减去空白部分的面积。
18.10平方米
【分析】三角形面积=底×高÷2,底延长1米后,面积增加2平方米,即1×高÷2=2,
高为4米,原三角形面积为5×4÷2=10(平方米)。
【详解】2×2÷1=4(米)
5×4÷2=10(平方米)
答:原来三角形的面积是10平方米。
19.见详解
【分析】根据阴影部分的面积与梯形面积的关系进行判断即可。
【详解】答:东东的说法正确。因为根据图示可知,三个图形中阴影部分的面积都等于梯形面积的一半。所以阴影部分的面积相等。
【点睛】本题主要考查组合图形的面积的计算。
20.1810平方厘米
【分析】观察图形可知,要粉刷的面积分三部分,一部分是底是10厘米,高是8厘米的三角形面积,一部分是长是80厘米,宽是10厘米的长方形面积;一部分是上底是10厘米,下底是16厘米,高是5厘米的梯形面积;根据三角形面积公式:面积=底×高÷2;长方形面积公式:面积=长×宽;梯形面积公式:面积=(上底+下底)×高÷2,代入数据,求出它们的面积,再相加,最后再乘2,即可解答。
【详解】[10×8÷2+80×10+(10+16)×5÷2]÷2
=[80÷2+800+26×5÷2]×2
=[40+800+130÷2]×2
=[840+65]×2
=905×2
=1810(平方厘米)
答:需要粉刷的面积有1810平方厘米。
【点睛】本题考查组合图形的面积求法,把组合图形分成规矩图形,再根据规矩图形的面积公式进行解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:多边形的面积(试题)数学五年级上册苏教版
一、选择题
1.下图平行线间三个图形的面积相比较,( )。
A.三个图形的面积相等 B.三角形的面积最大
C.平行四边形的面积最小 D.梯形面积最大
2.如图ABCD为长方形,EFCD为平行四边形,比较阴影部分甲,乙的面积,( )。
A.甲大 B.乙大 C.甲乙一样大 D.无法确定
3.一个平行四边形的底是10厘米,高是6厘米。如果把它的底和高分别乘3,那么它的面积( )。
A.扩大3倍 B.扩大6倍 C.扩大9倍 D.无法确定
4.如图,梯形被分为平行四边形和三角形,三角形的面积是32平方厘米,梯形的面积是( )平方厘米。
A.32 B.64 C.96 D.128
5.如下图,阴影部分的面积是20平方厘米,那么平行四边形的面积是( )平方厘米。
A.20 B.30 C.40 D.50
6.一个长方形的长去掉4厘米后,面积就减少了20平方厘米,剩下的部分正好是一个正方形,原来的长方形的面积是( )平方厘米。
A.25 B.45 C.5 D.20
二、填空题
7.一个平行四边形的底是32厘米,高是2分米,它的面积是( )平方分米,和它等底等高的三角形的面积是( )平方分米。
8.一个直角三角形的两条直角边分别是3厘米、4厘米,这个直角三角形的面积是( )平方厘米.如果这个直角三角形的斜边长是5厘米,那么这条斜边上的高是( )厘米.
9.下图中的阴影部分的面积是( )平方厘米。
10.一个梯形的面积是28平方米,它的高是7米,上底是3米,下底是( )米;用两个这样的梯形拼成一个平行四边形,平行四边形的面积是( )。
11.一堆钢管堆成了横截面为梯形,最上层有2根,最下层有12根,相邻两层相差1根,这堆钢管一共有( )根。
12.如图,把平行四边形剪成一个三角形和一个梯形,那么三角形的面积是( )cm2,梯形的面积是( )cm2。
13.如图,把一个平行四边形框架拉成长方形,面积增加了。原来平行四边形的高是( )cm。
14.一块梯形田地,它的上下底之和是120米,高是30米,面积是( )平方米。
三、解答题
15.一个梯形下底是上底的3倍,如果把上底延长8厘米,就得到一个平行四边形,且面积增加24平方厘米,这个梯形面积是多少平方厘米?
16.一块直角梯形地,它的下底是40米,如果上底增加38米,这块地就变成了正方形.原来梯形的面积是多少
17.(选做题)在如图中5个阴影所示的图形都是正方形,所标的数字是邻近线段的长度.那么阴影部分的总面积是多少?
18.如图,一个三角形的底长5米,如果底延长1米,那么面积就增加2平方米。那么原来三角形的面积是多少平方米?
19.如下图所示,梯形上底AB长3厘米,下底DC长6厘米,高4厘米,P为DC边上的任意一点。东东说点P在DC边上的任何地方阴影部分的面积都相等,也就是说下面3个图形阴影部分的面积相同。
你认为他的说法对吗?为什么?
20.2022年11月29日,搭载神舟十五号载人飞船的长征二号F遥十五运载火箭在酒泉卫星发射中心点火发射,中国航天事业又取得了一个新成就。实验小学组织学生到航天科技馆参观,科技馆内有一架火箭模型的标志牌(如下图)。如果要粉刷标志牌的正、反两面,需要粉刷的面积有多少平方厘米?
参考答案:
1.A
【分析】由图可知:三个图形的高(长)相等,长方形的宽,梯形的上底、下底,三角形的底都已知,再依据三者的面积公式求出它们的面积,比较即可。
【详解】假设长方形的长、三角形的高、梯形的高均为h,
长方形的面积为:4×h=4h
三角形的面积:8×h÷2=4h
梯形的面积:(2+6)×h÷2=4h
所以三个图形的面积相等,
故答案为:A
【点睛】此题主要考查三角形、梯形、长方形的面积公式,牢记公式是解题的关键。
2.C
【详解】因为长方形ABCD的高与平行四边形EFCD的高相等,那么长方形ABCD与平行四边形EFCD的面积相等,同时减去三角形CDF的面积,所以甲、乙两部分面积是相等的。
所以答案为:C
3.C
【分析】平行四边形的面积公式:s=ah,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积。
【详解】因为平行四边形的面积=底×高,如果把它的底和高分别乘3,那么它的面积就扩大3×3=9倍。
故答案为:C
【点睛】此题主要根据平行四边形的面积公式以及因数与积的变化规律解决问题。
4.C
【分析】根据图可知,三角形的底和平行四边形的底是相同的,高也是相同的,根据平行四边形的面积公式:底×高;三角形的面积公式:底×高÷2,由此即可知道等底等高的平行四边形的面积是三角形面积的2倍,则平行四边形的面积是:32×2=64(平方厘米),再加上三角形的面积即可求出梯形的面积。
【详解】32×2+32
=64+32
=96(平方厘米)
所以梯形的面积是96平方厘米。
故答案为:C
【点睛】本题主要考查平行四边形和三角形的面积公式,熟练掌握它们的面积公式并灵活运用。
5.C
【分析】观察图形可知,阴影部分是两个三角形的和,两个三角形的底的和等于平行四边形的底,三角形的高等于平行四边形的高;根据三角形面积公式:面积=底×高÷2;平行四边形面积公式:面积=底×高;由此可知,阴影部分的面积等于平行四边形面积的一半;即平行四边形面积=三角形面积×2,据此求出平行四边形面积。
【详解】20×2=40(平方厘米)
如下图,阴影部分的面积是20平方厘米,那么平行四边形的面积是40平方厘米。
故答案为:C
【点睛】解答本题的关键明确阴影部分的底的和与平行四边形的底的关系,阴影部分的高与平行四边形的高之间的关系是解答本题的关键。
6.B
【分析】根据长方形的面积公式:S=ab,那么b=S÷a,用减少的面积除以减少的长求出原来的宽,因为剩下的部分正好是一个正方形,所以宽加上4厘米就是原来的长,再把数据代入公式求出原来的面积。
【详解】20÷4=5(厘米)
(5+4)×5
=9×5
=45(平方厘米)
故答案为:B
【点睛】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
7. 6.4 3.2
【分析】先把32厘米化为3.2分米,然后根据平行四边形的面积=底×高和三角形的面积=底×高÷2,代入数据解答即可。
【详解】32厘米=3.2分米
3.2×2=6.4(平方分米)
3.2×2÷2=3.2(平方分米)
平行四边形的面积是6.4平方分米,和它等底等高的三角形的面积是3.2平方分米。
【点睛】本题主要考查了平行四边形和三角形面积公式的灵活应用,要熟练掌握相关公式。
8. 6 2.4
【解析】略
9.120
【分析】三个三角形的底的和是20厘米,根据三角形的面积=底×高求出阴影部分的面积。
【详解】20×12÷2
=240÷2
=120(平方厘米)
【点睛】考查了三角形的面积,学生应灵活应用其公式。
10. 5 56平方米
【分析】由“梯形的面积=(上底+下底)×高÷2”可得“梯形的下底=梯形的面积×2÷高-上底”,梯形的上底、高和面积已知,代入此关系式即可求解;用梯形的面积×2即可;据此解答。
【详解】28×2÷7-3
=56÷7-3
=8-3
=5(米)
28×2=56(平方米)
【点睛】本题主要考查梯形面积公式的灵活应用,牢记梯形面积公式是解题的关键。
11.77
【分析】相邻两层相差1根,那么用最下层的12根减去最上层的2根再加1,可以求出这堆钢管有几层,再根据梯形的面积=(上底+下底)×高÷2,列式求出这堆钢管一共多少根。
【详解】12-2+1=11(层)
(12+2)×11÷2
=14×11÷2
=77(根)
所以,这堆钢管一共有77根。
【点睛】本题的关键是灵活运用梯形的面积公式,找准梯形的高。
12. 15 35
【分析】由图可知,三角形底为6厘米,高为5厘米,由三角形面积=底×高÷2,代入数据可得。因为平行四边形对边相等,所以梯形的下底=平行四边形的底=10厘米,梯形上底:10-6=4厘米,由梯形面积=(上底+下底)×高÷2,代入数据可得。
【详解】三角形面积:5×6÷2
=30÷2
=15(平方厘米);
梯形上底:10-6=4(厘米)
梯形面积:(4+10)×5÷2
=14×5÷2
=70÷2
=35(平方厘米)
【点睛】此题考查的是三角形面积与梯形面积公式,能熟练应用并找到平行四边形对边相等的隐含条件是解题的关键。
13.10
【分析】根据长方形面积公式:S=长×宽,代入数值求出该长方形的面积,用求出的长方形面积减去40,可求出原来平行四边形的面积;通过对图的观察,在把平行四边形框架拉成长方形的过程中,平行四边形的底没有变,其底就是长方形的底,改变的是平行四边形的高,利用平行四边形面积公式:S=底×高,将数据代入可以求出原平行四边形的高。
【详解】由分析可得:
(20×12-40)÷20
=(240-40)÷20
=200÷20
=10(cm)
综上所述:如图,把一个平行四边形框架拉成长方形,面积增加了。原来平行四边形的高是10cm。
【点睛】本题考查了长方形、平行四边形面积公式的灵活运用,熟记公式是解题的关键。
14.1800
【分析】根据梯形的面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】120×30÷2
=3600÷2
=1800(平方米)
这块梯形田地的面积是1800平方米。
【点睛】此题主要考查梯形面积的实际应用,熟练掌握其公式是解题关键。
15.48平方厘米
【分析】根据题意,设上底为x厘米,下底为3x厘米,已知如果把上底延长8厘米,就得到一个平行四边形,也就是上底+8=下底,以此列方程求出上底和下底,因为增加的面积是三角形面积,底是8厘米,根据三角形面积=底×高÷2求出高,也就是梯形的高,再根据梯形的面积=(上底+下底)×高÷2即可解答。
【详解】解:设上底为x厘米,下底为3x厘米。
x+8=3x
2x=8
x=4
下底:4×3=12(厘米)
高:24×2÷8
=48÷8
=6(厘米)
梯形面积:(4+12)×6÷2
=16×6÷2
=96÷2
=48(平方厘米)
答:这个梯形面积是48平方厘米。
【点睛】此题主要考查学生对三角形和梯形面积公式的灵活应用,以及可以用方程解答未知数。
16.840平方米
【详解】(40-38+40)×40÷2
=42×40÷2
=840(平方米)
答:原来梯形的面积是840平方米.
17.244平方厘米
【分析】用大正方形的面积减去四个两条直角边是8和4的直角三角形的面积,再减去4个两条直角边是4和2的直角三角形的面积。据此解答。
【详解】(4+8+2+4)×(4+8+2+4)
=18×18
=324(平方厘米)
大直角三角形的面积:
8×4÷2
=32÷2
=16(平方厘米)
小直角三角形的面积:
4×2÷2
=8÷2
=4(平方厘米),
324-16×4-4×4
=324-64-16
=244(平方厘米)
答:阴影部分的面积是244平方厘米。
【点睛】本题的关键是根据图形,用大正方形的面积减去空白部分的面积。
18.10平方米
【分析】三角形面积=底×高÷2,底延长1米后,面积增加2平方米,即1×高÷2=2,
高为4米,原三角形面积为5×4÷2=10(平方米)。
【详解】2×2÷1=4(米)
5×4÷2=10(平方米)
答:原来三角形的面积是10平方米。
19.见详解
【分析】根据阴影部分的面积与梯形面积的关系进行判断即可。
【详解】答:东东的说法正确。因为根据图示可知,三个图形中阴影部分的面积都等于梯形面积的一半。所以阴影部分的面积相等。
【点睛】本题主要考查组合图形的面积的计算。
20.1810平方厘米
【分析】观察图形可知,要粉刷的面积分三部分,一部分是底是10厘米,高是8厘米的三角形面积,一部分是长是80厘米,宽是10厘米的长方形面积;一部分是上底是10厘米,下底是16厘米,高是5厘米的梯形面积;根据三角形面积公式:面积=底×高÷2;长方形面积公式:面积=长×宽;梯形面积公式:面积=(上底+下底)×高÷2,代入数据,求出它们的面积,再相加,最后再乘2,即可解答。
【详解】[10×8÷2+80×10+(10+16)×5÷2]÷2
=[80÷2+800+26×5÷2]×2
=[40+800+130÷2]×2
=[840+65]×2
=905×2
=1810(平方厘米)
答:需要粉刷的面积有1810平方厘米。
【点睛】本题考查组合图形的面积求法,把组合图形分成规矩图形,再根据规矩图形的面积公式进行解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
