平面图形的面积课件(共16张ppt)六年级数学下册苏教版
文档属性
| 名称 | 平面图形的面积课件(共16张ppt)六年级数学下册苏教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
平面图形的面积
点我
阴影图形的面积:
移动
割补
转换
例1.如图,圆的半径是2cm,等腰直角三角形的底边长16cm,求阴影部分面积。
法一:
分析:移动阴影部分的面积
梯形的上底:2×2=4(厘米)
梯形的面积:(4+16)×2÷2 =20(平方厘米)
答:阴影部分的面积是16平方厘米。
三角形的面积:4×2÷2 =4(平方厘米)
阴影的面积:20-4 =16(平方厘米)
①
②
③
④
例1.如图,圆的半径是2cm,等腰直角三角形的底边长16cm,求阴影部分面积。
法二:
分析:移动阴影部分的面积
答:阴影部分的面积是16平方厘米。
三角形的底:16÷2=8(厘米)
两个三角形的面积:
(8×2÷2)×2 =16(平方厘米)
例1.如图,圆的半径是2cm,等腰直角三角形的底边长16cm,求阴影部分面积。
法三:
分析:不移动
阴影部分的面积= 13.72+2.28=16(平方厘米)
③+④的面积=梯形的面积-半圆的面积
梯形的面积:(4+16)×2÷2 =20(平方厘米)
①
②
③
④
半圆的面积:3.14×2×2÷2 =6.28 (平方厘米)
③+④的面积=20-6.28=13.72(平方厘米)
①+②的面积 = 半圆的面积-三角形的面积
三角形的面积:4×2÷2 =4 (平方厘米)
①+②的面积=6.28-4=2.28 (平方厘米)
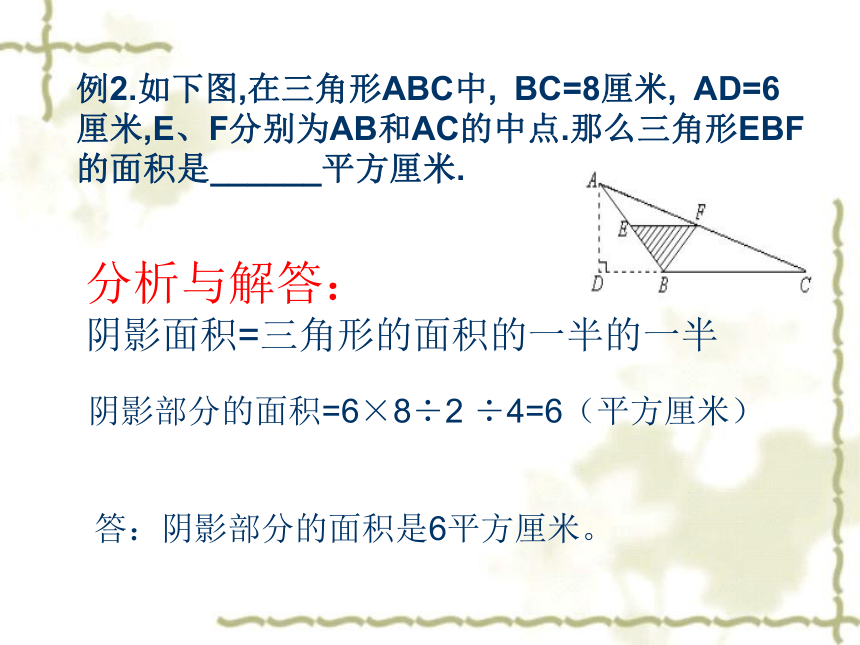
例2.如下图,在三角形ABC中, BC=8厘米, AD=6厘米,E、F分别为AB和AC的中点.那么三角形EBF的面积是______平方厘米.
分析与解答:
阴影面积=三角形的面积的一半的一半
阴影部分的面积=6×8÷2 ÷4=6(平方厘米)
答:阴影部分的面积是6平方厘米。
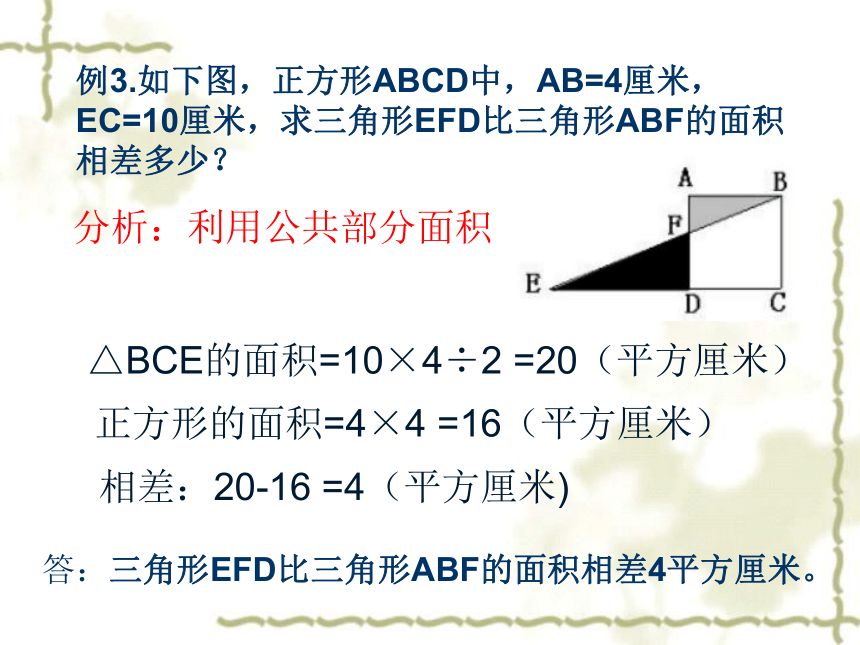
例3.如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求三角形EFD比三角形ABF的面积相差多少?
分析:利用公共部分面积
△BCE的面积=10×4÷2 =20(平方厘米)
正方形的面积=4×4 =16(平方厘米)
相差:20-16 =4(平方厘米)
答:三角形EFD比三角形ABF的面积相差4平方厘米。
例4.如图是两个完全一样的直角三角形重叠在一起,按照图中的已知条件求阴影部分的面积(单位:厘米)。
分析:利用公共部分面积
空白梯形的上底:120-40=80(厘米)
空白梯形的面积:
(80+120)×30÷2 =3000(平方厘米)
答:阴影部分的面积是3000平方厘米。
例5.大正方形的边长是6厘米,小正方形的边长是4厘米,求阴影部分的面积。
分析与解答:
阴影面积=用整体图形面积-空白图形的面积
6×6 + 4×4=52(平方厘米)
答:阴影部分的面积是14平方厘米。
6×6 ÷2=18(平方厘米)
(6+4)×4 ÷2=20(平方厘米)
52-18-20=14(平方厘米)
例6.(45中小升初试题)如图所示,求阴影部分的面积(单位:厘米)。
分析与解答:割补法
阴影面积=4×6=24(平方厘米)
答:阴影部分的面积是24平方厘米。
三角形的等高模型(等面积法)
定义:三角形面积的大小,取决于三角形底和高的乘积。
1、等底等高的两个三角形面积相等;
2、两个三角形高相等,面积之比等于底之比;
两个三角形底相等,面积之比等于高之比。
3、狼牙模型(一半模型):三角形面积等
于与它等底等高的平行四边形面积的一半。
拓展
A
B
C
D
【例1】长方形 ABCD 的面积为 36cm2,E、F、G 为各边中点,H 为 AD 边上任意一点,问阴影部分面积是多少?
分析:如图,连接BH,HC
面积①=面积②,面积③=面积④,面积⑤=面积⑥
阴影面积=面积②+面积③+面积⑥-S△BEF
答:阴影部分的面积是13.5平方厘米。
①
②
③
④
阴影的面积=18-4.5=13.5(平方厘米)
⑤
⑥
面积②+面积③+面积⑥=长方形面积的一半
例2. 如右图,阴影部分的面积和平行四边形ABCD的面积比是( );如果阴影部分的面积是16平方厘米,则平行四边形的面积是( )平方厘米。
分析与解答:狼牙模型
一半模型
1:2
32
例7.这个圆的半径是10厘米,求
(1)大正方形的面积是多少平方厘米?
(2)小正方形的面积是多少平方厘米?
分析与解答:
大正方形的边长等于圆的直径
小正方形的对角线是圆的直径
大正方形的面积:10×2=20(厘米)
20×20=400(平方厘米)
小正方形的面积: 20×20÷2=200(平方厘米)
例8.(如图,已知四条线段的长分别是:AB=2厘米,CE=6厘米,CD=5厘米,AF=4厘米,并且有两个直角。求四边形ABCD的面积。
分析与解答:割补法
大三角形的面积:5×4÷2=10(平方厘米)
小三角形的面积: 2×6÷2=6(平方厘米)
四边形ABCD的面积: 10+6=16(平方厘米)
答:四边形ABCD的面积是16平方厘米。
例9.如图所示,△ABC是等腰直角三角形,求阴影部分的面积(单位:厘米)。
分析与解答:整体图形-空白图形
圆的的面积:3.14×1×1=3.14(平方厘米)
三角形的面积: 2×2÷2=2(平方厘米)
阴影部分的面积: 3.14-2=1.14(平方厘米)
答:阴影部分的面积是1.14平方厘米。
平面图形的面积
点我
阴影图形的面积:
移动
割补
转换
例1.如图,圆的半径是2cm,等腰直角三角形的底边长16cm,求阴影部分面积。
法一:
分析:移动阴影部分的面积
梯形的上底:2×2=4(厘米)
梯形的面积:(4+16)×2÷2 =20(平方厘米)
答:阴影部分的面积是16平方厘米。
三角形的面积:4×2÷2 =4(平方厘米)
阴影的面积:20-4 =16(平方厘米)
①
②
③
④
例1.如图,圆的半径是2cm,等腰直角三角形的底边长16cm,求阴影部分面积。
法二:
分析:移动阴影部分的面积
答:阴影部分的面积是16平方厘米。
三角形的底:16÷2=8(厘米)
两个三角形的面积:
(8×2÷2)×2 =16(平方厘米)
例1.如图,圆的半径是2cm,等腰直角三角形的底边长16cm,求阴影部分面积。
法三:
分析:不移动
阴影部分的面积= 13.72+2.28=16(平方厘米)
③+④的面积=梯形的面积-半圆的面积
梯形的面积:(4+16)×2÷2 =20(平方厘米)
①
②
③
④
半圆的面积:3.14×2×2÷2 =6.28 (平方厘米)
③+④的面积=20-6.28=13.72(平方厘米)
①+②的面积 = 半圆的面积-三角形的面积
三角形的面积:4×2÷2 =4 (平方厘米)
①+②的面积=6.28-4=2.28 (平方厘米)
例2.如下图,在三角形ABC中, BC=8厘米, AD=6厘米,E、F分别为AB和AC的中点.那么三角形EBF的面积是______平方厘米.
分析与解答:
阴影面积=三角形的面积的一半的一半
阴影部分的面积=6×8÷2 ÷4=6(平方厘米)
答:阴影部分的面积是6平方厘米。
例3.如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求三角形EFD比三角形ABF的面积相差多少?
分析:利用公共部分面积
△BCE的面积=10×4÷2 =20(平方厘米)
正方形的面积=4×4 =16(平方厘米)
相差:20-16 =4(平方厘米)
答:三角形EFD比三角形ABF的面积相差4平方厘米。
例4.如图是两个完全一样的直角三角形重叠在一起,按照图中的已知条件求阴影部分的面积(单位:厘米)。
分析:利用公共部分面积
空白梯形的上底:120-40=80(厘米)
空白梯形的面积:
(80+120)×30÷2 =3000(平方厘米)
答:阴影部分的面积是3000平方厘米。
例5.大正方形的边长是6厘米,小正方形的边长是4厘米,求阴影部分的面积。
分析与解答:
阴影面积=用整体图形面积-空白图形的面积
6×6 + 4×4=52(平方厘米)
答:阴影部分的面积是14平方厘米。
6×6 ÷2=18(平方厘米)
(6+4)×4 ÷2=20(平方厘米)
52-18-20=14(平方厘米)
例6.(45中小升初试题)如图所示,求阴影部分的面积(单位:厘米)。
分析与解答:割补法
阴影面积=4×6=24(平方厘米)
答:阴影部分的面积是24平方厘米。
三角形的等高模型(等面积法)
定义:三角形面积的大小,取决于三角形底和高的乘积。
1、等底等高的两个三角形面积相等;
2、两个三角形高相等,面积之比等于底之比;
两个三角形底相等,面积之比等于高之比。
3、狼牙模型(一半模型):三角形面积等
于与它等底等高的平行四边形面积的一半。
拓展
A
B
C
D
【例1】长方形 ABCD 的面积为 36cm2,E、F、G 为各边中点,H 为 AD 边上任意一点,问阴影部分面积是多少?
分析:如图,连接BH,HC
面积①=面积②,面积③=面积④,面积⑤=面积⑥
阴影面积=面积②+面积③+面积⑥-S△BEF
答:阴影部分的面积是13.5平方厘米。
①
②
③
④
阴影的面积=18-4.5=13.5(平方厘米)
⑤
⑥
面积②+面积③+面积⑥=长方形面积的一半
例2. 如右图,阴影部分的面积和平行四边形ABCD的面积比是( );如果阴影部分的面积是16平方厘米,则平行四边形的面积是( )平方厘米。
分析与解答:狼牙模型
一半模型
1:2
32
例7.这个圆的半径是10厘米,求
(1)大正方形的面积是多少平方厘米?
(2)小正方形的面积是多少平方厘米?
分析与解答:
大正方形的边长等于圆的直径
小正方形的对角线是圆的直径
大正方形的面积:10×2=20(厘米)
20×20=400(平方厘米)
小正方形的面积: 20×20÷2=200(平方厘米)
例8.(如图,已知四条线段的长分别是:AB=2厘米,CE=6厘米,CD=5厘米,AF=4厘米,并且有两个直角。求四边形ABCD的面积。
分析与解答:割补法
大三角形的面积:5×4÷2=10(平方厘米)
小三角形的面积: 2×6÷2=6(平方厘米)
四边形ABCD的面积: 10+6=16(平方厘米)
答:四边形ABCD的面积是16平方厘米。
例9.如图所示,△ABC是等腰直角三角形,求阴影部分的面积(单位:厘米)。
分析与解答:整体图形-空白图形
圆的的面积:3.14×1×1=3.14(平方厘米)
三角形的面积: 2×2÷2=2(平方厘米)
阴影部分的面积: 3.14-2=1.14(平方厘米)
答:阴影部分的面积是1.14平方厘米。
