2.2.2直线的两点式方程 课件(共20张PPT)
文档属性
| 名称 | 2.2.2直线的两点式方程 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 41.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
2.2.2 直线的两点式方程
第 二 章 直线和圆的方程
人教A版2019选修第一册
学习目标
1.掌握直线的两点式方程和截距式方程.
2.会选择适当的方程形式求直线方程.
3.能用直线的两点式方程与截距式方程解答有关问题.
复习导入
确定直线位置的几何要素有两类:
直线上一点和方向
两点确定一条直线
过点P (x0,y0),斜率为k的直线l的点斜式方程为:
y-y0=k(x-x0)
点斜式的特例——斜截式:y=kx+b
情境导入
我们知道,给定一点和一个方向可以唯一确定一条直线.这样,在平面直角坐标系中,给定一个点P0(x0,y0)和斜率k(或倾斜角),就能唯一确定一条直线.
若给定直线上两点p1(x1,y1) p2(x2,y2),你能否得出直线的方程呢
直线的两点式方程
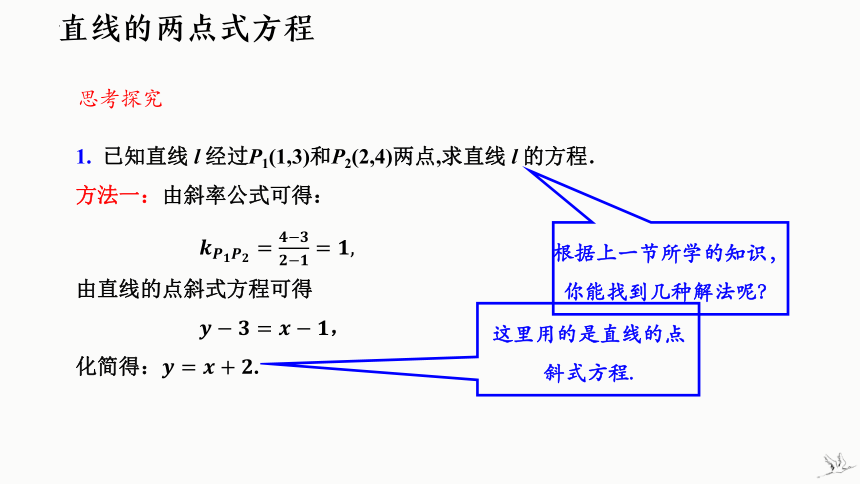
1. 已知直线 l 经过P1(1,3)和P2(2,4)两点,求直线 l 的方程.
方法一:由斜率公式可得:
由直线的点斜式方程可得
,
化简得:.
根据上一节所学的知识,你能找到几种解法呢?
这里用的是直线的点斜式方程.
思考探究
直线的两点式方程
方法二:设直线方程为:y=kx+b(k≠0),由于 l 经过点P1和P2,
所以将两点坐标代入可得:
解方程组得:
所以,直线方程为: y=x+2.
还有什么简单的方法来求解呢?
1. 已知直线 l 经过P1(1,3)和P2(2,4)两点,求直线 l 的方程.
这里用的是待定系数法和方程的数学思想.
直线的两点式方程
已知直线l经过两点P1(x1,y1),P2(x2,y2) (其中x1≠x2,y1≠y2),因为两点确定一条直线,所以直线l是唯一确定的.
即直线l上任意一点P(x,y)坐标与的两点P1,P2的坐标之间有唯一确定的关系.
思考:它们的坐标之间的关系是什么呢?
直线的两点式方程
答:因为所以直线的斜率为k存在,由斜率公式可得,
所以由直线的点斜式方程可得 .
又因为,
思考:一般的,已知直线 l 经过和()两点,如何求直线 l 的方程.
上式可以变形为
这就是经过两点和()的直线方程.
直线的两点式方程
直线的两点式方程
经过两点P1(x1,y1),P2(x2,y2) (其中x1≠x2,y1≠y2)的直线的方程为:
=.
我们把它叫做直线的两点式方程,简称两点式.
当x1=x2时,直线P1P2垂直于x轴,直线方程为______;
当y1=y2时,直线P1P2垂直于y轴,直线方程为______.
x=x1
y=y1
两点式的适用条件:直线的两点式方程,
不能用来表示平行于坐标轴或与坐标轴重合的直线的方程.
直线的两点式方程
3x-5y+6=0
直线的两点式方程
直线的两点式方程
解:将A(a,0),B(0,b)的坐标代入两点式得:
即
x
l
B(0,b)
A(a,0)
O
y
4.已知直线 l 与 x 轴的交点为A(a,0),与 y 轴的交点为B(0,b),其中a≠0,b≠0. 求直线 l 的方程.
直线的截距式方程
直线的截距式方程
直线方程由直线在 x 轴和 y 轴的截距确定,所以我们把上面的方程叫做
直线的截距式方程.
直线在x轴的截距
直线在y轴的截距
思考:直线的截距式方程的适用条件是什么?
它是两点式的特例,所以仍然不能表示平行于坐标轴和与坐标轴重合的直线;另外由于a,b在分母上,所以a≠0且b≠0,也不能表示过原点的直线.
直线的截距式方程
1.求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程.
分析:截距均为0时,设方程为y=kx,截距均不为0时,设为截距式求解.
解:①当截距均为0时,设方程为y=kx,把P(-5,4)代入上式得,
即直线方程为.
②当截距均不为0时,设直线方程为
把P(-5,4)代入上式得
直线方程为-x-y=1,即x+y+1=0.
综上:直线方程为或x+y+1=0.
直线的截距式方程
2.设直线 l 的方程为(a+1)x+y+2-a=0(a∈R).
若直线 l 在两坐标轴上的截距互为相反数,求直线 l 的方程.
解:①当直线过原点时,该直线在x轴和y轴上的截距为零,显然互为相反数.
∴a=2,方程即为3x+y=0.
②当直线不过原点时,a≠2,化简可得,得,
即整理得a+1=-1,∴a=-2,即直线方程为x-y-4=0.
直线的截距式方程
直线的截距式方程
直线的截距式方程
直线方程名称 直线方程形式 适用范围
点斜式
斜截式
两点式
截距式
不垂直x轴(斜率k存在)
不垂直x轴(斜率k存在)
不垂直两个坐标轴
不垂直两个坐标
轴且不经过原点
各类方程的适用范围
课堂小结
课堂小结
2.2.2 直线的两点式方程
第 二 章 直线和圆的方程
人教A版2019选修第一册
学习目标
1.掌握直线的两点式方程和截距式方程.
2.会选择适当的方程形式求直线方程.
3.能用直线的两点式方程与截距式方程解答有关问题.
复习导入
确定直线位置的几何要素有两类:
直线上一点和方向
两点确定一条直线
过点P (x0,y0),斜率为k的直线l的点斜式方程为:
y-y0=k(x-x0)
点斜式的特例——斜截式:y=kx+b
情境导入
我们知道,给定一点和一个方向可以唯一确定一条直线.这样,在平面直角坐标系中,给定一个点P0(x0,y0)和斜率k(或倾斜角),就能唯一确定一条直线.
若给定直线上两点p1(x1,y1) p2(x2,y2),你能否得出直线的方程呢
直线的两点式方程
1. 已知直线 l 经过P1(1,3)和P2(2,4)两点,求直线 l 的方程.
方法一:由斜率公式可得:
由直线的点斜式方程可得
,
化简得:.
根据上一节所学的知识,你能找到几种解法呢?
这里用的是直线的点斜式方程.
思考探究
直线的两点式方程
方法二:设直线方程为:y=kx+b(k≠0),由于 l 经过点P1和P2,
所以将两点坐标代入可得:
解方程组得:
所以,直线方程为: y=x+2.
还有什么简单的方法来求解呢?
1. 已知直线 l 经过P1(1,3)和P2(2,4)两点,求直线 l 的方程.
这里用的是待定系数法和方程的数学思想.
直线的两点式方程
已知直线l经过两点P1(x1,y1),P2(x2,y2) (其中x1≠x2,y1≠y2),因为两点确定一条直线,所以直线l是唯一确定的.
即直线l上任意一点P(x,y)坐标与的两点P1,P2的坐标之间有唯一确定的关系.
思考:它们的坐标之间的关系是什么呢?
直线的两点式方程
答:因为所以直线的斜率为k存在,由斜率公式可得,
所以由直线的点斜式方程可得 .
又因为,
思考:一般的,已知直线 l 经过和()两点,如何求直线 l 的方程.
上式可以变形为
这就是经过两点和()的直线方程.
直线的两点式方程
直线的两点式方程
经过两点P1(x1,y1),P2(x2,y2) (其中x1≠x2,y1≠y2)的直线的方程为:
=.
我们把它叫做直线的两点式方程,简称两点式.
当x1=x2时,直线P1P2垂直于x轴,直线方程为______;
当y1=y2时,直线P1P2垂直于y轴,直线方程为______.
x=x1
y=y1
两点式的适用条件:直线的两点式方程,
不能用来表示平行于坐标轴或与坐标轴重合的直线的方程.
直线的两点式方程
3x-5y+6=0
直线的两点式方程
直线的两点式方程
解:将A(a,0),B(0,b)的坐标代入两点式得:
即
x
l
B(0,b)
A(a,0)
O
y
4.已知直线 l 与 x 轴的交点为A(a,0),与 y 轴的交点为B(0,b),其中a≠0,b≠0. 求直线 l 的方程.
直线的截距式方程
直线的截距式方程
直线方程由直线在 x 轴和 y 轴的截距确定,所以我们把上面的方程叫做
直线的截距式方程.
直线在x轴的截距
直线在y轴的截距
思考:直线的截距式方程的适用条件是什么?
它是两点式的特例,所以仍然不能表示平行于坐标轴和与坐标轴重合的直线;另外由于a,b在分母上,所以a≠0且b≠0,也不能表示过原点的直线.
直线的截距式方程
1.求经过点P(-5,4),且在两坐标轴上的截距相等的直线方程.
分析:截距均为0时,设方程为y=kx,截距均不为0时,设为截距式求解.
解:①当截距均为0时,设方程为y=kx,把P(-5,4)代入上式得,
即直线方程为.
②当截距均不为0时,设直线方程为
把P(-5,4)代入上式得
直线方程为-x-y=1,即x+y+1=0.
综上:直线方程为或x+y+1=0.
直线的截距式方程
2.设直线 l 的方程为(a+1)x+y+2-a=0(a∈R).
若直线 l 在两坐标轴上的截距互为相反数,求直线 l 的方程.
解:①当直线过原点时,该直线在x轴和y轴上的截距为零,显然互为相反数.
∴a=2,方程即为3x+y=0.
②当直线不过原点时,a≠2,化简可得,得,
即整理得a+1=-1,∴a=-2,即直线方程为x-y-4=0.
直线的截距式方程
直线的截距式方程
直线的截距式方程
直线方程名称 直线方程形式 适用范围
点斜式
斜截式
两点式
截距式
不垂直x轴(斜率k存在)
不垂直x轴(斜率k存在)
不垂直两个坐标轴
不垂直两个坐标
轴且不经过原点
各类方程的适用范围
课堂小结
课堂小结
