数学七上第3章整式的加减复习题训练及解析
文档属性
| 名称 | 数学七上第3章整式的加减复习题训练及解析 |  | |
| 格式 | zip | ||
| 文件大小 | 568.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-20 08:15:22 | ||
图片预览




文档简介
复习题训练及解析(一)
用字母表示问题中的数量关系
1.-a(a是有理数)表示的数是 ( )
A.正数 B.负数
C.正数或负数 D.任意有理数
【解析】选D.因为a可以表示任意有理数,则-a表示的数是任意有理数.
【易错提醒】带“-”号的数不一定是负数.比如当a是负数时-a是正数,当a是0时,-a也是0.
2.某市2014年6月份某一天的温差为11℃,最高气温为t℃,则最低气温可表示为 ( )
A.(11+t)℃ B.(11-t)℃
C.(t-11)℃ D.(-t-11)℃
【解析】选C.由已知可知,最高气温-最低气温=温差,从而求出最低气温=最高气温-温差=(t-11)℃.
3.一个两位数,十位上的数字是a,个位上的数字是b,这个两位数用含有字母的式子表示是 ( )
A.ab B.10a+b C.10b+a D.10(a+b)
【解析】选B.用十位上的数字乘以10,加 ( http: / / www.21cnjy.com )上个位上的数字,即可列出这个两位数.因为十位数字为a,个位数字为b,所以这个两位数可以表示为10a+b.
4.(2013·长春模拟)为了帮助灾区重建 ( http: / / www.21cnjy.com )家园,某班全体学生积极捐款,捐款金额共480元,其中18名女生人均捐款a元,则该班男生共捐款 元.
【解析】由题意知18名女生共捐款18a元,所以该班男生共捐款(480-18a)元.
答案:(480-18a)
5.(2013·三明中考)观察下列各数,它们是按一定规律排列的,则第n个数是 .
,,,,,…
【解题指南】解答本题的两个关键
(1)找到分子与分母的关系,明确分子比分母小1.
(2)分母是2的整数次幂.
【解析】因为2=21,4=22,8=23,16=24,32=25,…
所以第n个数的分母是2n,
又因为分子都比相应的分母小1,
所以第n个数的分子为2n-1,
所以第n个数是.
答案:
6.如图所示是一些由若干个花盆组成的形如三 ( http: / / www.21cnjy.com )角形的图案,那么当图案的每条边上有n个花盆时(n≥2,n为整数),该三角形图案所含的花盆总数是多少
( http: / / www.21cnjy.com )
【解析】由题意,知第一个图 ( http: / / www.21cnjy.com )案有3个花盆,第2个图案有6个花盆,第3个图案有9个花盆,当图案的每条边上有n个花盆时,是第(n-1)个图案,所以该图案的花盆总数为3(n-1)盆,即(3n-3)盆.
【一题多解】由题意知,每一个图案都有三 ( http: / / www.21cnjy.com )条边,第1个图案的每一条边上有2个花盆,但是3个顶点处的花盆都重复算了一次,所以第1个图案共有花盆(2×3-3)个;第2个图案的每一条边上有3个花盆,但是3个顶点处的花盆都重复算了一次,所以第2个图案共有花盆(3×3-3)个;第3个图案的每一条边上有4个花盆,但是3个顶点处的花盆都重复算了一次,所以第3个图案共有花盆(4×3-3)个.……
所以第(n-1)个图案的每一条边上 ( http: / / www.21cnjy.com )有n个花盆,但是3个顶点处的花盆都重复算了一次,所以第(n-1)个图案共有花盆(n×3-3)个,即(3n-3)盆.
用代数式表示实际问题
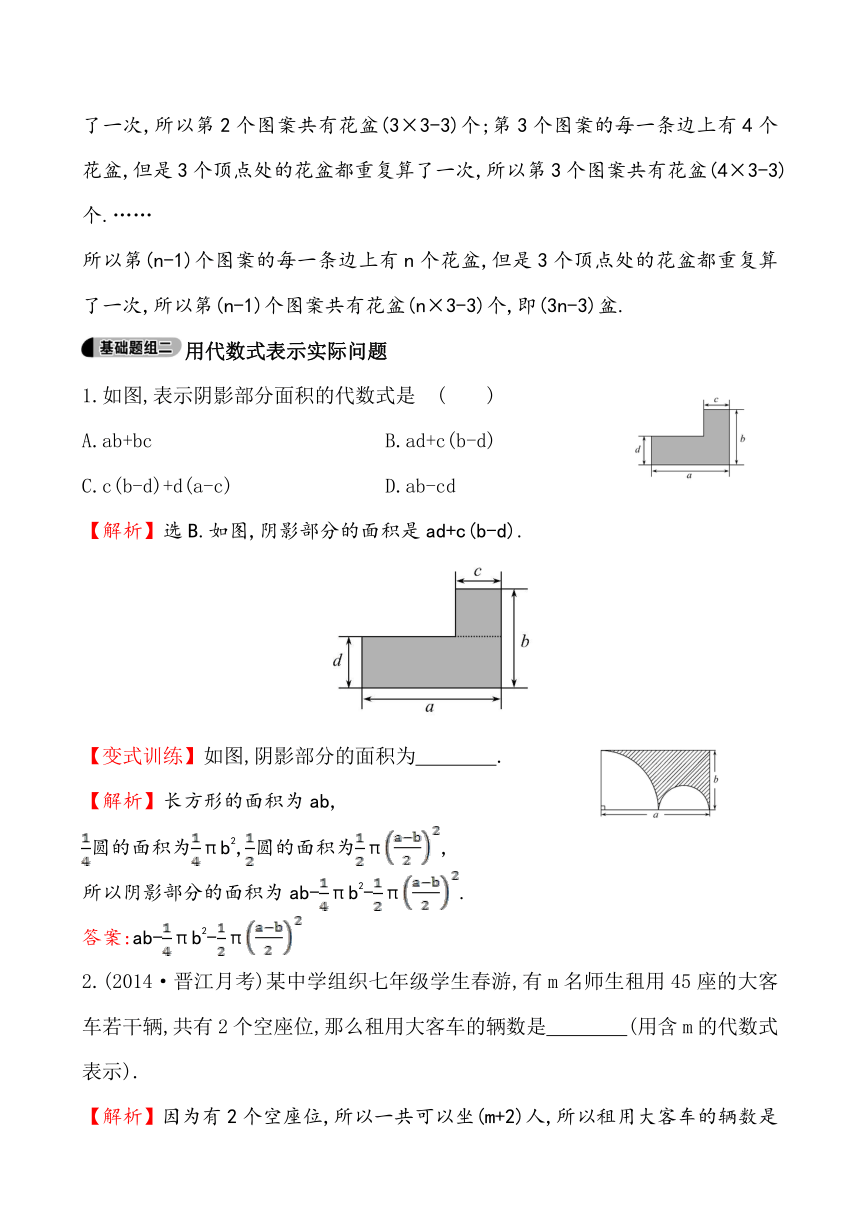
1.如图,表示阴影部分面积的代数式是 ( )
A.ab+bc B.ad+c(b-d)
C.c(b-d)+d(a-c) D.ab-cd
【解析】选B.如图,阴影部分的面积是ad+c(b-d).
( http: / / www.21cnjy.com )
【变式训练】如图,阴影部分的面积为 .
【解析】长方形的面积为ab,
圆的面积为πb2,圆的面积为π,
所以阴影部分的面积为ab-πb2-π.
答案:ab-πb2-π
2.(2014·晋江月考)某中学组 ( http: / / www.21cnjy.com )织七年级学生春游,有m名师生租用45座的大客车若干辆,共有2个空座位,那么租用大客车的辆数是 (用含m的代数式表示).
【解析】因为有2个空座位,所以一共可以坐(m+2)人,所以租用大客车的辆数是.
答案:
3.(2013·长春中考)吉林广播电视塔“五 ( http: / / www.21cnjy.com )一”假期第一天接待游客m人,第二天接待游客n人,则这两天平均每天接待游客 人(用含m,n的代数式表示).
【解析】两天接待游客总数为(m+n),所以其平均数为.
答案:
4.(2013·邵阳中考) ( http: / / www.21cnjy.com )2013年五月份,由于H7N9禽流感的影响,我市鸡肉的价格下降了10%,设鸡肉原来的价格为a元/千克,则五月份的价格为 .
【解析】因为原来价格为a元/千克,五月份比原来下降了10%,所以五月份的价格为a(1-10%)=0.9a元/千克.
答案:0.9a元/千克
【互动探究】如果本题中五月份的价格为a元/千克,那么原来的价格为多少
【解析】可设原来的价格为x元/千克,可得x(1-10%)=a,
所以x=a,即原来的价格为a元/千克.
5.老师利用假期带学生外 ( http: / / www.21cnjy.com )出游玩,已知每张车票50元,甲车车主说,如果乘我的车,师生全部可以享受八折优惠;乙车车主说,如果乘我的车,学生7折优惠,老师买全票.已知这个老师带了x名学生,分别写出乘甲、乙两车所需的车费.
【解析】乘甲车需要的费用为50(x+1)×80%=40(x+1)元;
乘乙车的费用为50×70%x+50=(35x+50)元.
答:乘甲车的费用为40(x+1)元,乘乙车的费用为(35x+50)元.
【错在哪?】作业错例 课堂实拍
七年级一班筹备元旦晚会,作为班长的小明 ( http: / / www.21cnjy.com ),带了100元去购买物品,已知他买了单价为a元的彩笔n支,b元的笔记本m个,回来的时候小明还剩下 元.
( http: / / www.21cnjy.com )
(1)找错:第 步出现错误.
(2)纠错:
答案:(1)③
(2)所以剩下的钱的金额为(100-an-bm)元.
复习题训练及解析(二)
列代数式表示数量关系
1.有三个连续偶数,最大的一个是2n+2,则最小的一个可以表示为 ( )
A.2n-2 B.2n C.2n+1 D.2n-1
【解析】选A.根据连续的偶数相差是2,可知:三个连续的偶数中,最大的比最小的大4.故三个数中最小的一个为:2n+2-4=2n-2.
【变式训练】有三个连续偶数,中间的一个是2n,这三个偶数的和是 .
【解析】根据连续的偶数相差是2,可知:小的偶数是2n-2,大的偶数是2n+2,所以三个偶数的和可列代数式为2n-2+2n+2n+2=6n.
答案:6n
2.(2014·宝山一模)一个两位数,十位数字是x,个位数字是y,如果把它们的位置交换,得到的数是 ( )
A.y+x B.yx C.10y+x D.10x+y
【解析】选C.因为十位数字是x,个位数字是y,
所以交换后的数个位数字是x,十位数字是y,
所以得到的数为10y+x.
【知识归纳】用代数式表示多位整数的方法
1.先用它的各个数位上的数字乘以数字所在数位上的单位.
2.再把所得的积相加.
【互动探究】如果已知a是两位数,b是一位数,把a接写在b的后面,就成为一个三位数.这个三位数可表示成 .
【解析】因为a是两位数,b是一位数,所以b扩大了100倍,所以这个三位数可表示成100b+a.
答案:100b+a
3.(2013·同安区一模)“比a的2倍大的数”用代数式表示为 .
【解析】因为a的2倍是2a,所以比a的2倍大的数是2a+.
答案:2a+
4.(2013·潍坊中考)当n等于1, ( http: / / www.21cnjy.com )2,3…时,由白色小正方形和黑色小正方形组成的图形分别如图所示.则第n个图形中白色小正方形和黑色小正方形的个数总和等于 (用n表示,n是正整数).
( http: / / www.21cnjy.com )
【解题指南】解答本题的三个步骤
(1)观察图案的变化趋势.
(2)从第1个图形进行分析,运用从特殊到一般的探索方式,找出黑白正方形个数增加的变化规律.
(3)用含有n的代数式进行表示.
【解析】第1个图形中有1个白色小正 ( http: / / www.21cnjy.com )方形和4×1个黑色小正方形;第2个图形中有22个白色小正方形和4×2个黑色小正方形;第3个图形中有32个白色小正方形和4×3个黑色小正方形;…第n个图形中有n2个白色小正方形和4n个黑色小正方形;因此第n个图形中白色小正方形和黑色小正方形的个数总和等于n2+4n.
答案:n2+4n
5.(2013·铁岭中考)某商店压了一批 ( http: / / www.21cnjy.com )商品,为尽快售出,该商店采取如下销售方案:将原来每件m元,加价50%,再做两次降价处理,第一次降价30%,第二次降价10%.经过两次降价后的价格为 元(结果用含m的代数式表示).
【解析】根据题意得:
m(1+50%)(1-30%)(1-10%)=0.945m(元).
答案:0.945m
6.用代数式表示:
(1)x的与y的倒数的和.
(2)a,b两数之积与a,b两数之和的差.
(3)a,b的差除以a,b的积.
(4)x的36%与y的平方的差.
【解析】(1)x+.(2)ab-(a+b).(3).
(4)36%x-y2.
【易错提醒】在列代数式时应注意句子中 ( http: / / www.21cnjy.com )出现的“的”字,逐层分析,逐步把问题中与数量有关的词语用代数式表示出来,同时要注意括号的使用,如第(2)题的结果不能写成ab-a+b的形式.
7.一次数学测验中,小亮、小杰、小丽三人的平均分为a分,小亮、小杰的平均分为b分,小杰、小丽的平均分为c分.
那么:
(1)小丽得几分
(2)小亮得几分
(3)小杰得几分
【解析】(1)小丽得(3a-2b)分.
(2)小亮得(3a-2c)分.
(3)小杰得[3a-(3a-2b)-(3a-2c)]分.
【错在哪?】作业错例 课堂实拍
设甲数为x,乙数为y,用代数式表示:
①甲、乙两数的平方差.
②甲、乙两数的差的平方.
③甲数的倒数的5倍与乙数的立方和.
( http: / / www.21cnjy.com )
(1)找错:①与②错在把“平方差”和“差的平方”混了.③错在 .
(2)纠错:
答案:(1)漏掉了甲数的倒数.
(2)
复习题训练及解析(三)
求代数式的值
1.(2013·怀化中考)已知m=1,n=0,则代数式m+n的值为 ( )
A.-1 B.1 C.-2 D.2
【解析】选B.当m=1,n=0时,m+n=1+0=1.
2.当x=-1时,代数式x2-2x+7的值是 ( )
A.10 B.8 C.6 D.4
【解析】选A.x=-1时,x2-2x+7=(-1)2-2×(-1)+7=1+2+7=10.
【易错提醒】如果代入的值是负数,要注意加上括号,以免在符号上出错.如本题代入后等于1+2+7而不是-1-2+7.
3.如果a+b=2,那么代数式3a+3b的值是 ( )
A.6 B.5 C.4 D.12
【解析】选A.因为a+b=2,所以3(a+b)=3×2=6.
【变式训练】(2014·高港区二模)若2a+3b-5=0,则多项式6a+9b-12的值是 .
【解析】因为2a+3b-5=0,所以2a+3b=5,
所以6a+9b-12=3(2a+3b)-12=3×5-12=3.
答案:3
4.(2013·吉林中考)若a-2b=3,则2a-4b-5= .
【解析】2a-4b-5=2(a-2b)-5=2×3-5=1.
答案:1
【互动探究】若2+a-2b=0,那么2a-4b-5的值是多少
【解析】因为2+a-2b=0,所以a-2b=-2,
所以2a-4b-5=2(a-2b)-5=2×(-2)-5=-9.
【知识归纳】整体代入法
求代数式的值最常用的方法就是代入法 ( http: / / www.21cnjy.com ),即把字母所表示的数值直接代入,计算求值.有时给出的条件不是字母的具体值,就需要先进行化简,求出字母的值,但有时很难求出字母的值或者根本就求不出字母的值,根据题目特点,将一个代数式的值整体代入,求值时方便又快捷,这种整体代入的方法经常用到.
5.(2014·宜春模拟)已知a=b-2,则(a-b)2+(b-a)+1的值为 .
【解析】因为a=b-2,所以a-b=-2,b-a=2,
所以原式=(-2)2+2+1=7.
答案:7
6.已知=3,求代数式-的值.
【解析】因为=3,所以=.
所以-
=2×-×
=2×3-×
=6-
=.
求代数式的值的应用
1.某种导火线的燃烧速度是0. ( http: / / www.21cnjy.com )81cm/s,爆破员跑开的速度是5m/s,为在点火后使爆破员跑到150m以外的安全地区,导火线的长度可以为 ( )
A.22cm B.23cm
C.24cm D.25cm
【解析】选D.导火线的长度是与安全地区的路程相关,设点火后使爆破员跑到xm以外的安全地区,那么所需导火线的长度至少为×0.81cm.当x=150时,导火线的长度为×0.81=24.3(cm),故导火线的长度至少为24.3cm,只有D项符合要求.
2.(2013·苏州中考)按照如图所示的操作步骤,若输入x的值为2,则输出的值为 .
【解题指南】解答本题的两个步骤
(1)按运算程序列出代数式.
(2)把x的值代入所列的代数式.
【解析】由图可知输出的结果为(x+3)2-5,
当x=2时,(x+3)2-5=(2+3)2-5=25-5=20.
答案:20
3.(2013·红河州中考)下列图形是 ( http: / / www.21cnjy.com )由一些小正方形和实心圆按一定规律排列而成的,如图所示,按此规律排列下去,第20个图形中有 个实心圆.
( http: / / www.21cnjy.com )
【解析】第(1)个图形中有4+2×0=4个实心圆;
第(2)个图形中有4+2×1=6个实心圆;
第(3)个图形中有4+2×2=8个实心圆;…,
第(n)个图形中有4+2×(n -1)个实心圆;
所以第20个图形中有4+2×19=42个实心圆.
答案:42
4.若梯形的上底为a,下底为b,高为h,则梯形面积为 ,当a=2cm,
b=4 cm,h=3cm时,梯形的面积为 .
【解析】梯形的面积公式为S=(上底+下底)×高÷2,
即S=(a+b)h,
当a=2cm,b=4cm,h=3cm时,
S=×(2+4)×3=×6×3=9(cm2).
答案:(a+b)h 9cm2
5.一块三角尺的形状和尺寸如图所示,a为直角边的长,r为圆孔的半径.
(1)求阴影部分的面积S.
(2)当a=8cm,r=1.5cm时.求S的值(π取3.14).
( http: / / www.21cnjy.com )
【解析】(1)因为三角形的面积为a2,
圆的面积为πr2,
所以阴影部分的面积S=a2-πr2.
(2)当a=8cm,r=1.5cm,π取3.14时,
S=a2-πr2=×82-3.14×1.52
=32-7.065=24.935(cm2).
【错在哪?】作业错例 课堂实拍
已知a=,b=,求代数式a+2b的值.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:
答案:(1)① (2)
复习题训练及解析(三)
单项式
1.在x2-x,2πx3y,,-4,a中单项式的个数是 ( )
A.1 B.2 C.3 D.4
【解析】选C.所给式子中,单项式有2πx3y,-4,a,共3个.
【易错提醒】不是单项式,凡是分母中有字母的代数式都不是单项式.
2.(2013·德宏州中考)-4a2b的次数是 ( )
A.3 B.2 C.4 D.-4
【解析】选A.因为单项式-4a2b中所有字母指数的和为2+1=3,所以此单项式的次数为3.
3.(2013·岳阳中考)单项式-5x2y的系数是 .
【解析】因为-5x2y=-5·x2y,所以该单项式的系数是-5.
答案:-5
【变式训练】(2014·椒江区二模)单项式-2πy的系数为 ( )
A.-2π B.-2 C.2 D.2π
【解析】选A.因为-2πy=-2π·y,
所以-2πy的系数为-2π.
4.(2013·淮安中考)观察一列单项式:x,3x2,5x3,7x,9x2,11x3,…,则第2013个单项式是 .
【解题指南】解答本题的两个关键
(1)知道系数是连续的奇数.
(2)知道指数是按1,2,3的顺序三个一循环.
【解析】本题这一列单项式的系数是1,3,5 ( http: / / www.21cnjy.com ),7,9,…,是连续的奇数,可用2n-1表示.所以第2013个单项式的系数为2×2013-1=4025.字母x的指数是1,2,3,1,2,3,…,三个一循环,2013÷3=671,所以指数为3.所以第2013个单项式是4025x3.
答案:4025x3
5.已知-2xmyn+1的次数为2,求3m+3n-5的值.
【解析】因为-2xmyn+1的次数为2,所以m+n+1=2.
所以m+n=1(向所求方向进行转化).
所以3m+3n=3,所以3m+3n-5=3-5=-2.
【变式训练】如果(m+1)2x2yn+1是关于x,y的六次单项式,求m,n的值.
【解析】因为(m+1)2x2yn+1是关于x,y的六次单项式,
所以2+n+1=6,而m+1≠0,解得m≠-1,n=3.
多项式
1.多项式-πx2y+22xy-1是 ( )
A.五次三项式 B.四次三项式
C.二次三项式 D.三次三项式
【解析】选D.多项式-πx2y+22xy-1是三次三项式.
【易错提醒】本题要注意两个问题
(1)π不是字母,所以第一项-πx2y的次数是3次,不是4次.
(2)单项式的次数是所有字母的指数和,而不是所有指数的和,所以第二项22xy的次数是2次,不是4次.
【变式训练】下列多项式是二次三项式的是 ( )
A.2x2+3 B.3x2+2
C.2x+3y+1 D.2x2+3y+1
【解析】选D.选项A,B是二次二项式,选项C是一次三项式,选项D是二次三项式.
2.(2013·佛山中考)多项式1+2xy-3xy2的次数及最高次项的系数分别
是 ( )
A.3,-3 B.2,-3 C.5,-3 D.2,3
【解析】选A.因为多项式的次数就是多项式中次数最高项的次数,所以1+2xy-3xy2的次数是3,这一项的系数是-3.
3.(2013·济宁中考)如果整式xn-2-5x+2是关于x的三次三项式,那么n等于
( )
A.3 B.4 C.5 D.6
【解析】选C.由多项式次数的概念,整式xn-2-5x+2是关于x的三次三项式,所以n-2=3,n=5.
4.(2014·赤峰期中检测)多项式-x2+2x+3xyz是 次 项式.
【解析】多项式-x2+2x+3xyz有三项,最高次项的次数是3,所以该多项式是三次三项式.
答案:三 三
5.如果2xm+1+3x+1是关于x的三次多项式,求m的值.
【解析】因为2xm+1+3x+1是关于x的三次多项式,所以x的最高次数是3,即m+1=3.
解得m=2.
升幂排列与降幂排列
1.把多项式2x2+3x3-x+5x4-1按字母x降幂排列是 ( )
A.2x2+3x3-x+5x4-1 B.5x4+3x3+2x2-1-x
C.-1-x+2x2+3x3+5x4 D.5x4+3x3+2x2-x-1
【解析】选D.多项式2x2+ ( http: / / www.21cnjy.com )3x3-x+5x4-1的各项是2x2,3x3,-x,5x4,-1,所以按字母x降幂排列为5x4+3x3+2x2-x-1.
2.对于多项式22m2+3m-1,下列说法正确的是 ( )
A.它是关于m的四次三项式
B.它的常数项是1
C.它是按m的降幂排列
D.它是按m的升幂排列
【解析】选C.多项式22m2+3m-1 ( http: / / www.21cnjy.com )的各项的次数分别为2,1,0.由于多项式的次数是“多项式中次数最高的项的次数”,所以多项式22m2+3m-1的次数是2,因此A不正确.它的常数项是-1,选项B不正确.
在多项式22m2+3m-1中,22m2的次数是2,3m的次数是1,因此是按m的降幂排列,选项C正确,D不正确.
3.把多项式-2x+1-x3+x2按字母x的降幂排列为 .
【解析】-2x+1-x3+x2按字母x的降幂排列为-x3+x2-2x+1.
答案:-x3+x2-2x+1
4.把多项式4a3b-3ab2+a4-5b5按字母b的升幂排列是 .
【解析】把多项式4a3b-3ab2+a4-5b5按b的升幂排列为a4+4a3b-3ab2-5b5.
答案:a4+4a3b-3ab2-5b5
【互动探究】如果是按字母a的降幂排列,结果应该是什么 与按b的升幂排列的结果有什么关系
【解析】把多项式4a3b-3ab2+a4-5b5按字母a的降幂排列为a4+4a3b-3ab2-5b5,与按b的升幂排列的结果一样.
5.将多项式5a2b5+ab-3a3b3-6a4b2+1按要求排列:
(1)按字母a降幂排列.
(2)按字母b升幂排列.
【解析】(1)按字母a降幂排列为-6a4b2-3a3b3+5a2b5+ab+1.
(2)按字母b升幂排列为1+ab-6a4b2-3a3b3+5a2b5.
【错在哪?】作业错例 课堂实拍
把下列多项式按字母x先进行降幂排列,再进行升幂排列.
12x-10x2+8.
( http: / / www.21cnjy.com )
(1)找错:出现错误的是 .
(2)纠错:
答案:(1)①②
(2)①是-10x2+12x+8,②是8+12x-10x2.
复习题训练及解析(四)
同类项的概念及应用
1.(2014·太原期末模拟)下列各式中,与x2y是同类项的是 ( )
A.xy2 B.x2+y C.-x2y D.3x2y2
【解析】选C. xy2和3x2y2与x2y中相同字母的指数不相同;x2+y是多项式,所以A,B,D均不是x2y的同类项.
2.下列各组中的两项不是同类项的是 ( )
A.-25mn和3nm B.7.2a2b和a2b
C.2x3y2和-3x2y3 D.-125和93
【解析】选C.因为2x3y2和-3x2y3的相同字母的指数不同,所以不是同类项.
【易错提醒】同类项中的指数相同,指的是 ( http: / / www.21cnjy.com )相同字母的指数相同,而不是常数的指数,所以2x3y2和-3x2y3不是同类项,-125和93是同类项.
【变式训练】下列各组中的两项是同类项的是 ( )
A.m3n4和m4n3 B.ab与ab
C.m3与a3 D.2x与2y
【解析】选B.m3n4和m4n3相同字母的指数不同,不是同类项;m3与a3字母不同,不是同类项;2x与2y字母不同,不是同类项.
3.若3xmy3与-x2yn是同类项,则(-m)n等于 ( )
A.6 B.-6 C.8 D.-8
【解题指南】解答本题的两个步骤
(1)根据同类项的定义求出m,n的值.
(2)代入(-m)n计算.
【解析】选D.因为3xmy3与-x2yn是同类项,所以m=2,n=3,所以(-m)n=(-2)3=-8.
4.(2013·凉山州中考)如果单项式-xa+1y3与ybx2是同类项,那么a,b的值分别为
( )
A.a=2,b=3 B.a=1,b=2
C.a=1,b=3 D.a=2,b=2
【解析】选C.因为-xa+1y3与ybx2是同类项,所以a+1=2,b=3,所以a=1,b=3.
5.写出3a2的一个同类项: .
【解析】答案不唯一,只要只含字母a,且a的指数是2,都是3a2的一个同类项,如-2a2.
答案:-2a2(答案不唯一)
6.(2014·松原实验期末检测)当a= 时,5xa-1y2与-3x2y2是同类项.
【解析】由题意得a-1=2,所以a=3.
答案:3
7.如果单项式5xmy4与单项式xy2n是同类项,那么m= ,n= .
【解析】根据同类项的条件:m=1,4=2n,即n=2.
答案:1 2
【变式训练】已知代数式2a3bn+1与-3am-2b2是同类项,则2m+3n= .
【解析】由同类项的定义,可知m-2=3,n+1=2,
解得m=5,n=1,则2m+3n=13.
答案:13
8.判断下列各组式子是不是同类项:
(1)22ab3与-3ab3. (2)0.2abc与7ac.
(3)-5x2y3与4x3y2. (4)π与10.
【解析】(1)是同类项.(2)不是同类项.(3)不是同类项.(4)是同类项.
【易错提醒】常数项都是同类项,要注意π是常数,本题中的π和10是同类项.
9.若3ambn-1与-a4b2是同类项,求(n-m)2014的值.
【解析】由同类项的概念得m=4,2=n-1,
则:m=4,n=3.
所以(n-m)2014=(3-4)2014=(-1)2014=1.
【错在哪?】作业错例 课堂实拍
多项式3x2y-3+5x2y+2xy2+5有哪几项 其中哪些是同类项
( http: / / www.21cnjy.com )
(1)找错:出现错误的是 .
(2)纠错: .
答案:(1)②
(2) 3x2y,+5x2y是同类项
复习题训练及解析(五)
合并同类项
1.(2013·梧州中考)化简a+a= ( )
A.2 B.a2 C.2a2 D.2a
【解析】选D.根据合并同类项的法则:系数相加减,字母及字母的指数不变,可得a+a=2a.
【变式训练】(2014·廊坊一模)计算a+2a= ( )
A.2a2 B.3a2
C.a(1+a) D.3a
【解析】选D.a+2a=(1+2)a=3a.
2.(2013·苏州中考)计算-2x2+3x2的结果为 ( )
A.-5x2 B.5x2 C.-x2 D.x2
【解析】选D.原式=(-2+3)x2=x2.
【变式训练】下列计算中,正确的是 ( )
A.-a-a=0 B.3a+2a=5a2
C.a3+a3=a6 D.a2+a2=2a2
【解析】选D.-a-a=-2a,3a+2a=5a,a3+a3=2a3,a2+a2=2a2.
3.若代数式ax+bx合并同类项后结果为零,则a,b满足的关系式为 ( )
A.a+b=1 B.a=b C.a-b=0 D.a+b=0
【解析】选D.ax+bx=(a+b)x=0,所以a+b=0.
【知识归纳】代数式值恒为0的条件
(1)一个代数式的值恒为0,并不是代数式中的所有字母均为0,而是指代数式中的字母无论取何值,其值均为0.
(2)如果代数式的值恒为0,那么其合并后的系数一定是0.
4.若单项式-5xm-1y2与4x3yn-1能够合并,则m-n= .
【解析】根据题意得单项式-5xm-1y2与4x3yn-1是同类项,
所以m-1=3,n-1=2,
解得m=4,n=3,则m-n=4-3=1.
答案:1
5.合并同类项:
(1)4a2+3b2-2ab-3a2-5b2.
(2)3xy2-5xy+0.5x2y-3xy2-4.5x2y.
【解析】(1)原式=(4a2-3a2)+(3b2-5b2)-2ab=a2-2b2-2ab.
(2)原式=(3xy2+0.5x2y-3xy2-4.5x2y)-5xy=-4x2y-5xy.
【变式训练】如果把x-y看作一个因式,那么代数式2(x-y)2-(x-y)+3(x-y)2-4(x-y)合并后的结果是什么
【解析】2(x-y)2-(x-y)+3(x-y)2-4(x-y)
=5(x-y)2-5(x-y).
6.求多项式5x2+4-3x2-5x-2x2-5+6x的值,其中x=-3.
【解析】5x2+4-3x2-5x-2x2-5+6x
=5x2-3x2-2x2-5x+6x+4-5
=(5-3-2)x2+(-5+6)x+(4-5)
=x-1.
当x=-3时,原式=-3-1=-4.
合并同类项的应用
1.如图,阴影部分的面积是 ( )
( http: / / www.21cnjy.com )
A.xy B.xy C.5xy D.2xy
【解题指南】解答图形面积问题的基本方法
(1)转化:把不规则图形的面积转化为规则图形的面积的和或差.
(2)计算:由规则图形的面积表示出不规则图形的面积.
【解析】选A.阴影部分面积为:3x×2y-0.5x×y-×x×2y=6xy-xy-xy=xy.
2.若a<0,则2014a-10|a|等于 ( )
A.2004a B.-2024a
C.2024a D.-2014a
【解析】选C.2014a-10|a|=2014a+10a=2024a.
3.已知A等于2xy,B是A的3倍,C是B的,那么A+B+C= .
【解析】由题意知B=3×2xy=6xy,C=×6xy=4xy,
所以A+B+C=2xy+6xy+4xy=12xy.
答案:12xy
4.某仓库原有货物mt,上午运进8车货物,下午运出3车货物,后来又运进2车货物,如果每车载货at,那么仓库中现有货物 t.
【解析】仓库中现有货物m+8a-3a+2a=(m+7a)t.
答案:(m+7a)
5.七年级一班为建立“图书角”,各组同学 ( http: / / www.21cnjy.com )踊跃捐书.一组捐x本书,二组捐的书是一组的2倍还多2本,三组捐的书是一组的3倍少1本,则三个小组共捐书
本.
【解析】由题意知,二组捐了(2x+2)本,三组捐了(3x-1)本,所以三个小组共捐书:
x+2x+2+3x-1=(6x+1)(本).
答案:(6x+1)
6.(2014·晋中模拟)要使代数式a3+2ma2-5a2+1中不含有a2的项,则m= .
【解析】由已知要使代数式a3+2ma2-5a2+1中不含有a2的项,可得2m-5=0,即m=.
答案:
7.我校七年级(1)班三个兴趣小组为灾区捐款 ( http: / / www.21cnjy.com ),舞蹈小组的同学共捐款x元,美术小组的同学捐款比舞蹈小组捐款的2倍还多8元,篮球小组的同学捐款比美术小组捐款的一半少6元,这三个小组的同学一共捐款多少元
【解析】由题意知,美术小组的同学捐款为(2x+8)元,篮球小组的同学捐款为元,三个小组同学的捐款数为:x+(2x+8)+
=x+2x+8+x+4-6=(4x+6)元.
【错在哪?】作业错例 课堂实拍
合并同类项5y-2x2y-3y+3x2y.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错: .
答案:(1)②
(2)原式=2y+x2y
复习题训练及解析(六)
去括号法则及应用
1.(2014·南昌模拟)去括号-(a-b)结果正确的是 ( )
A.a-b B.a+b C.-a-b D.b-a
【解析】选D.-(a-b)=-a+b=b-a.
【易错提醒】括号前是“-”号,括号里各项都改变符号,本题易错选C.
2.下列代数式中,去括号的结果等于a-b-c的是 ( )
A.-(a+b+c) B.-b-(c-a)
C.a-(b-c) D.-c+(b-a)
【解析】选B.-(a+b+c)=-a-b-c;-b-(c-a)=-b-c+a=a-b-c;a-(b-c)=a-b+c;
-c+(b-a)=-c+b-a=-a+b-c.
【变式训练】下面去括号错误的是 ( )
A.3(a-b)=3a-b B.a+(b-c)=a+b-c
C.a-(b+c)=a-b-c D.-(a-2b)=-a+2b
【解析】选A.3(a-b)=3a-3b.
3.下列运算正确的是 ( )
A.-2(3x-1)=-6x-1
B.-2(3x-1)=-6x+1
C.-2(3x-1)=-6x-2
D.-2(3x-1)=-6x+2
【解析】选D.-2(3x-1)=-6x+2,所以A,B,C选项错误.
【知识归纳】去括号时,括号前有负数相 ( http: / / www.21cnjy.com )乘,可以运用去括号法则将括号内的项都改变符号,再与负数的绝对值相乘;也可以直接运用乘法分配律将负数与括号内各项相乘,注意不能漏乘.
4.(2013·上海中考)计算:2(a-b)+3b= .
【解析】2(a-b)+3b=2a-2b+3b=2a+b.
答案:2a+b
5.(2013·厦门中考)计算:5a+2b+(3a—2b).
【解析】5a+2b+(3a—2b)=5a+2b+3a—2b
=8a.
6.先化简,再求值:3a2-[7a2-2a-3(a2-a)+1],其中a=-1.
【解析】3a2-[7a2-2a-3(a2-a)+1]
=3a2-(7a2-2a-3a2+3a+1)
=3a2-(4a2+a+1)
=3a2-4a2-a-1
=-a2-a-1.
当a=-1时,原式=-(-1)2-(-1)-1=-1.
添括号法则及应用
1.下列等式:(1)-a-b=-(a-b).(2)-a+b=-(-b+a).(3)4-3x=-(3x-4).其中一定成立的等式的个数是 ( )
A.0个 B.1个 C.2个 D.3个
【解析】选C.因为-a-b=-(a+b),-a+b=-(-b+a),4-3x=-(3x-4),所以一定成立的等式有2个.
【知识拓展】添括号与去括号的关系
(1)添括号与去括号是两个互逆的过程.
(2)添括号是否正确,可通过去括号进行验证.
2.不改变3a2-2b2-b+a+ab的 ( http: / / www.21cnjy.com )值,把二次项放在前面有“+”号的括号里,一次项放在前面有“-”号的括号里,下列各式正确的是 ( )
A.+(3a2+2b2+ab)-(b+a)
B.+(-3a2-2b2-ab)-(b-a)
C.+(3a2-2b2+ab)-(b-a)
D.+(3a2-2b2+ab)-(b+a)
【解析】选C.3a2-2b2-b+a+ab=3a2-2b2+ab-b+a
=+(3a2-2b2+ab)-(b-a).
3.已知a-b=1,则代数式3-2a+2b的值是 ( )
A.-1 B.1 C.-5 D.5
【解析】选B.3-2a+2b=3-2(a-b)=3-2×1=1.
【一题多解】选B.本题也可用下面的方法求解,由a-b=1,得a=b+1,代入可得3-2a+2b=3-2(b+1)+2b
=3-2b-2+2b=1.
4.(2014·宿州质检)若2a-b=1,则4a-2b-1= .
【解析】4a-2b-1=2(2a-b)-1=2×1-1=1.
答案:1
5.a3+3a2-2a=a3+( ),
a-4-2b-c=(a-2b)-( ).
【解析】a3+3a2-2a=a3+(3a2-2a),
a-4-2b-c=(a-2b)-(c+4).
答案:3a2-2a c+4
6.按要求把多项式x3-5x2-4x+9添上括号.
(1)把它放在前面带有“+”号的括号里.
(2)把它放在前面带有“-”号的括号里.
(3)把后两项放在前面带有“-”号的括号里.
(4)把后三项放在前面带有“-”号的括号里.
【解析】(1)x3-5x2-4x+9=+(x3-5x2-4x+9).
(2)x3-5x2-4x+9
=-(-x3+5x2+4x-9).
(3)x3-5x2-4x+9=x3-5x2-(4x-9).
(4)x3-5x2-4x+9=x3-(5x2+4x-9).
【错在哪?】作业错例 课堂实拍
先去括号,再合并同类项:
-(2a2+5)-(3a2-2)-2(-4a2-1).
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:原式 .
答案:(1)①
(2) =-2a2-5-3a2+2+8a2+2=(-2-3+8)a2+(2+2-5)=3a2-1
复习题训练及解析(七)
整式的加减运算
1.已知有一整式与(2x2+5x-2)的和为(2x2+5x+4),则此整式为 ( )
A.2 B.6
C.10x+6 D.4x2+10x+2
【解析】选B.此整式为(2x2+5x+4)-(2x2+5x-2)=2x2+5x+4-2x2-5x+2=6.
【易错提醒】本题要理清三个整式之间的关系,避免出现这个数等于(2x2+5x+4)+(2x2+5x-2)这样的错误.
【变式训练】比多项式5a2-2a-3ab少5a2-2ab的多项式是 ( )
A.-2a-ab B.-2a-5ab
C.-2a+5ab D.2a+ab
【解析】选A.5a2-2a-3ab-(5a2-2ab)=5a2-2a-3ab
-5a2+2ab=-2a-ab.
2.一个多项式减去x2-2y2等于x2+y2,则这个多项式是 ( )
A.-2x2+y2 B.2x2-y2
C.x2-2y2 D.-x2+2y2
【解析】选B.这个多项式是(x2-2y2)+(x2+y2)=2x2-y2.
【互动探究】这两个多项式的和是多少
【解析】这两个多项式的和是(2x2-y2)+(x2-2y2)=3x2-3y2.
3.若M和N都是3次多项式,则M+N为 ( )
A.3次多项式 B.6次多项式
C.次数不超过3的整式 D.次数不低于3的整式
【解析】选C.因为M和N都是3次多项式,
所以M+N为次数不超过3的整式.
4.设a=x2+x,b=x-2,则a与b的大小关系为 .
【解析】由题意得a-b=x2+x-(x-2)=x2+2>0,
所以a>b.
答案:a>b
【知识拓展】作差法比较两个整式的大小
比较两个整式的大小,用作差法, ( http: / / www.21cnjy.com )如果差大于0,则被减数大于减数,如果差小于0,则被减数小于减数.例如,若A=a+b,B=a-b,则A与B的大小关系如何 因为A-B=a+b-(a-b)=a+b-a+b=2b,所以当b<0时,A0时,A>B.
5.已知多项式A=3x2-6x+5,B=2x2+7x-6,求2A-3B.
【解析】因为A=3x2-6x+5,B=2x2+7x-6,
所以2A-3B=2(3x2-6x+5)-3(2x2+7x-6)
=6x2-12x+10-6x2-21x+18=-33x+28.
6.化简求值:
3a2+(4a2-2a-1)-2(3a2-a+1),其中a=.
【解析】3a2+(4a2-2a-1)-2(3a2-a+1)
=3a2+4a2-2a-1-6a2+2a-2=a2-3.
当a=时,原式=()2-3=-3=-.
【变式训练】(2014·广州一模)先化简,再求值4(x-y)-2(3x+y)+1,其中x=1,y=-.
【解析】原式=4x-4y-6x-2y+1
=-2x-6y+1,
当x=1,y=-时,原式=-2×1-6×+1
=-2+2+1=1.
整式加减的实际应用
1.长方形一边等于3a-2b,另一边比它小a-b,则此长方形另一边的长等于
( )
A.4a-3b B.4a+b C.2a+b D.2a-b
【解析】选D.根据题意得:(3a-2b)-(a-b)=3a-2b-a+b=2a-b.
2.(2013·聊城中考)把地球看成 ( http: / / www.21cnjy.com )一个表面光滑的球体,假设沿地球赤道绕紧一圈钢丝,然后把钢丝加长,使钢丝圈沿赤道处处高出球面16cm,那么钢丝大约需要加长 ( )
A.102cm B.104cm C.106cm D.108cm
【解题指南】解答本题考查的知识及解题关键
(1)此题主要考查了圆的周长公式以及科学记数法.
(2)根据已知得出图形变化前后的周长是解题关键.
【解析】选A.设地球半径为rcm,
则地球的周长为2πrcm,
假设沿地球赤道绕紧一圈钢丝,然后把钢丝加长,使钢丝圈沿赤道处处高出球面16cm,
故此时钢丝围成的圆形的周长变为2π(r+16)cm,
所以钢丝大约需要加长:2π(r+16)-2πr≈100(cm)=102(cm).
3.一个长方形的相邻两边长分别为3m+2n和m+n,则这个长方形的周长为 .
【解析】这个长方形的周长为2(3m+2n+m+n)
=2(4m+3n)=8m+6n.
答案:8m+6n
4.已知三角形的第一边长为3a+2b,第二边比第一边长a-b,第三边比第二边短2a,求这个三角形的周长.
【解析】第一边长为3a+2b,
则第二边长为(3a+2b)+(a-b)=4a+b,
第三边长为(4a+b)-2a=2a+b,
所以这个三角形的周长为(3a+2b)+(4a+b)+(2a+b)=3a+2b+4a+b+2a+b=9a+4b.
5.一公园的成年人票价是15元,儿童买 ( http: / / www.21cnjy.com )半票,甲旅行团有x(名)成年人和y(名)儿童;乙旅行团的成年人数是甲旅行团成年人数的2倍,儿童数比甲旅行团儿童人数的2倍少8人,这两个旅行团的门票费用总和是多少
【解析】甲旅行团的门票费用:(15x+y)元,
乙旅行团的门票费用:[15×2x+(2y-8)]元,
所以(15x+y)+[15×2x+(2y-8)]
=15x+y+30x+15y-60=(45x+y-60)元.
即这两个旅行团的门票费用总和是元.
【错在哪?】作业错例 课堂实拍
求a2b-[a2b-2(3abc-a2c)-4a2c]-3abc的值,其中a=-1,b=-3,c=.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:原式
答案:(1)①
(2)
=-a2b+2a2c+3abc.
当a=-1,b=-3,c=时,
原式=-(-1)2×(-3)+2×(-1)2×+3×(-1)×(-3)×=3+1+
=8
用字母表示问题中的数量关系
1.-a(a是有理数)表示的数是 ( )
A.正数 B.负数
C.正数或负数 D.任意有理数
【解析】选D.因为a可以表示任意有理数,则-a表示的数是任意有理数.
【易错提醒】带“-”号的数不一定是负数.比如当a是负数时-a是正数,当a是0时,-a也是0.
2.某市2014年6月份某一天的温差为11℃,最高气温为t℃,则最低气温可表示为 ( )
A.(11+t)℃ B.(11-t)℃
C.(t-11)℃ D.(-t-11)℃
【解析】选C.由已知可知,最高气温-最低气温=温差,从而求出最低气温=最高气温-温差=(t-11)℃.
3.一个两位数,十位上的数字是a,个位上的数字是b,这个两位数用含有字母的式子表示是 ( )
A.ab B.10a+b C.10b+a D.10(a+b)
【解析】选B.用十位上的数字乘以10,加 ( http: / / www.21cnjy.com )上个位上的数字,即可列出这个两位数.因为十位数字为a,个位数字为b,所以这个两位数可以表示为10a+b.
4.(2013·长春模拟)为了帮助灾区重建 ( http: / / www.21cnjy.com )家园,某班全体学生积极捐款,捐款金额共480元,其中18名女生人均捐款a元,则该班男生共捐款 元.
【解析】由题意知18名女生共捐款18a元,所以该班男生共捐款(480-18a)元.
答案:(480-18a)
5.(2013·三明中考)观察下列各数,它们是按一定规律排列的,则第n个数是 .
,,,,,…
【解题指南】解答本题的两个关键
(1)找到分子与分母的关系,明确分子比分母小1.
(2)分母是2的整数次幂.
【解析】因为2=21,4=22,8=23,16=24,32=25,…
所以第n个数的分母是2n,
又因为分子都比相应的分母小1,
所以第n个数的分子为2n-1,
所以第n个数是.
答案:
6.如图所示是一些由若干个花盆组成的形如三 ( http: / / www.21cnjy.com )角形的图案,那么当图案的每条边上有n个花盆时(n≥2,n为整数),该三角形图案所含的花盆总数是多少
( http: / / www.21cnjy.com )
【解析】由题意,知第一个图 ( http: / / www.21cnjy.com )案有3个花盆,第2个图案有6个花盆,第3个图案有9个花盆,当图案的每条边上有n个花盆时,是第(n-1)个图案,所以该图案的花盆总数为3(n-1)盆,即(3n-3)盆.
【一题多解】由题意知,每一个图案都有三 ( http: / / www.21cnjy.com )条边,第1个图案的每一条边上有2个花盆,但是3个顶点处的花盆都重复算了一次,所以第1个图案共有花盆(2×3-3)个;第2个图案的每一条边上有3个花盆,但是3个顶点处的花盆都重复算了一次,所以第2个图案共有花盆(3×3-3)个;第3个图案的每一条边上有4个花盆,但是3个顶点处的花盆都重复算了一次,所以第3个图案共有花盆(4×3-3)个.……
所以第(n-1)个图案的每一条边上 ( http: / / www.21cnjy.com )有n个花盆,但是3个顶点处的花盆都重复算了一次,所以第(n-1)个图案共有花盆(n×3-3)个,即(3n-3)盆.
用代数式表示实际问题
1.如图,表示阴影部分面积的代数式是 ( )
A.ab+bc B.ad+c(b-d)
C.c(b-d)+d(a-c) D.ab-cd
【解析】选B.如图,阴影部分的面积是ad+c(b-d).
( http: / / www.21cnjy.com )
【变式训练】如图,阴影部分的面积为 .
【解析】长方形的面积为ab,
圆的面积为πb2,圆的面积为π,
所以阴影部分的面积为ab-πb2-π.
答案:ab-πb2-π
2.(2014·晋江月考)某中学组 ( http: / / www.21cnjy.com )织七年级学生春游,有m名师生租用45座的大客车若干辆,共有2个空座位,那么租用大客车的辆数是 (用含m的代数式表示).
【解析】因为有2个空座位,所以一共可以坐(m+2)人,所以租用大客车的辆数是.
答案:
3.(2013·长春中考)吉林广播电视塔“五 ( http: / / www.21cnjy.com )一”假期第一天接待游客m人,第二天接待游客n人,则这两天平均每天接待游客 人(用含m,n的代数式表示).
【解析】两天接待游客总数为(m+n),所以其平均数为.
答案:
4.(2013·邵阳中考) ( http: / / www.21cnjy.com )2013年五月份,由于H7N9禽流感的影响,我市鸡肉的价格下降了10%,设鸡肉原来的价格为a元/千克,则五月份的价格为 .
【解析】因为原来价格为a元/千克,五月份比原来下降了10%,所以五月份的价格为a(1-10%)=0.9a元/千克.
答案:0.9a元/千克
【互动探究】如果本题中五月份的价格为a元/千克,那么原来的价格为多少
【解析】可设原来的价格为x元/千克,可得x(1-10%)=a,
所以x=a,即原来的价格为a元/千克.
5.老师利用假期带学生外 ( http: / / www.21cnjy.com )出游玩,已知每张车票50元,甲车车主说,如果乘我的车,师生全部可以享受八折优惠;乙车车主说,如果乘我的车,学生7折优惠,老师买全票.已知这个老师带了x名学生,分别写出乘甲、乙两车所需的车费.
【解析】乘甲车需要的费用为50(x+1)×80%=40(x+1)元;
乘乙车的费用为50×70%x+50=(35x+50)元.
答:乘甲车的费用为40(x+1)元,乘乙车的费用为(35x+50)元.
【错在哪?】作业错例 课堂实拍
七年级一班筹备元旦晚会,作为班长的小明 ( http: / / www.21cnjy.com ),带了100元去购买物品,已知他买了单价为a元的彩笔n支,b元的笔记本m个,回来的时候小明还剩下 元.
( http: / / www.21cnjy.com )
(1)找错:第 步出现错误.
(2)纠错:
答案:(1)③
(2)所以剩下的钱的金额为(100-an-bm)元.
复习题训练及解析(二)
列代数式表示数量关系
1.有三个连续偶数,最大的一个是2n+2,则最小的一个可以表示为 ( )
A.2n-2 B.2n C.2n+1 D.2n-1
【解析】选A.根据连续的偶数相差是2,可知:三个连续的偶数中,最大的比最小的大4.故三个数中最小的一个为:2n+2-4=2n-2.
【变式训练】有三个连续偶数,中间的一个是2n,这三个偶数的和是 .
【解析】根据连续的偶数相差是2,可知:小的偶数是2n-2,大的偶数是2n+2,所以三个偶数的和可列代数式为2n-2+2n+2n+2=6n.
答案:6n
2.(2014·宝山一模)一个两位数,十位数字是x,个位数字是y,如果把它们的位置交换,得到的数是 ( )
A.y+x B.yx C.10y+x D.10x+y
【解析】选C.因为十位数字是x,个位数字是y,
所以交换后的数个位数字是x,十位数字是y,
所以得到的数为10y+x.
【知识归纳】用代数式表示多位整数的方法
1.先用它的各个数位上的数字乘以数字所在数位上的单位.
2.再把所得的积相加.
【互动探究】如果已知a是两位数,b是一位数,把a接写在b的后面,就成为一个三位数.这个三位数可表示成 .
【解析】因为a是两位数,b是一位数,所以b扩大了100倍,所以这个三位数可表示成100b+a.
答案:100b+a
3.(2013·同安区一模)“比a的2倍大的数”用代数式表示为 .
【解析】因为a的2倍是2a,所以比a的2倍大的数是2a+.
答案:2a+
4.(2013·潍坊中考)当n等于1, ( http: / / www.21cnjy.com )2,3…时,由白色小正方形和黑色小正方形组成的图形分别如图所示.则第n个图形中白色小正方形和黑色小正方形的个数总和等于 (用n表示,n是正整数).
( http: / / www.21cnjy.com )
【解题指南】解答本题的三个步骤
(1)观察图案的变化趋势.
(2)从第1个图形进行分析,运用从特殊到一般的探索方式,找出黑白正方形个数增加的变化规律.
(3)用含有n的代数式进行表示.
【解析】第1个图形中有1个白色小正 ( http: / / www.21cnjy.com )方形和4×1个黑色小正方形;第2个图形中有22个白色小正方形和4×2个黑色小正方形;第3个图形中有32个白色小正方形和4×3个黑色小正方形;…第n个图形中有n2个白色小正方形和4n个黑色小正方形;因此第n个图形中白色小正方形和黑色小正方形的个数总和等于n2+4n.
答案:n2+4n
5.(2013·铁岭中考)某商店压了一批 ( http: / / www.21cnjy.com )商品,为尽快售出,该商店采取如下销售方案:将原来每件m元,加价50%,再做两次降价处理,第一次降价30%,第二次降价10%.经过两次降价后的价格为 元(结果用含m的代数式表示).
【解析】根据题意得:
m(1+50%)(1-30%)(1-10%)=0.945m(元).
答案:0.945m
6.用代数式表示:
(1)x的与y的倒数的和.
(2)a,b两数之积与a,b两数之和的差.
(3)a,b的差除以a,b的积.
(4)x的36%与y的平方的差.
【解析】(1)x+.(2)ab-(a+b).(3).
(4)36%x-y2.
【易错提醒】在列代数式时应注意句子中 ( http: / / www.21cnjy.com )出现的“的”字,逐层分析,逐步把问题中与数量有关的词语用代数式表示出来,同时要注意括号的使用,如第(2)题的结果不能写成ab-a+b的形式.
7.一次数学测验中,小亮、小杰、小丽三人的平均分为a分,小亮、小杰的平均分为b分,小杰、小丽的平均分为c分.
那么:
(1)小丽得几分
(2)小亮得几分
(3)小杰得几分
【解析】(1)小丽得(3a-2b)分.
(2)小亮得(3a-2c)分.
(3)小杰得[3a-(3a-2b)-(3a-2c)]分.
【错在哪?】作业错例 课堂实拍
设甲数为x,乙数为y,用代数式表示:
①甲、乙两数的平方差.
②甲、乙两数的差的平方.
③甲数的倒数的5倍与乙数的立方和.
( http: / / www.21cnjy.com )
(1)找错:①与②错在把“平方差”和“差的平方”混了.③错在 .
(2)纠错:
答案:(1)漏掉了甲数的倒数.
(2)
复习题训练及解析(三)
求代数式的值
1.(2013·怀化中考)已知m=1,n=0,则代数式m+n的值为 ( )
A.-1 B.1 C.-2 D.2
【解析】选B.当m=1,n=0时,m+n=1+0=1.
2.当x=-1时,代数式x2-2x+7的值是 ( )
A.10 B.8 C.6 D.4
【解析】选A.x=-1时,x2-2x+7=(-1)2-2×(-1)+7=1+2+7=10.
【易错提醒】如果代入的值是负数,要注意加上括号,以免在符号上出错.如本题代入后等于1+2+7而不是-1-2+7.
3.如果a+b=2,那么代数式3a+3b的值是 ( )
A.6 B.5 C.4 D.12
【解析】选A.因为a+b=2,所以3(a+b)=3×2=6.
【变式训练】(2014·高港区二模)若2a+3b-5=0,则多项式6a+9b-12的值是 .
【解析】因为2a+3b-5=0,所以2a+3b=5,
所以6a+9b-12=3(2a+3b)-12=3×5-12=3.
答案:3
4.(2013·吉林中考)若a-2b=3,则2a-4b-5= .
【解析】2a-4b-5=2(a-2b)-5=2×3-5=1.
答案:1
【互动探究】若2+a-2b=0,那么2a-4b-5的值是多少
【解析】因为2+a-2b=0,所以a-2b=-2,
所以2a-4b-5=2(a-2b)-5=2×(-2)-5=-9.
【知识归纳】整体代入法
求代数式的值最常用的方法就是代入法 ( http: / / www.21cnjy.com ),即把字母所表示的数值直接代入,计算求值.有时给出的条件不是字母的具体值,就需要先进行化简,求出字母的值,但有时很难求出字母的值或者根本就求不出字母的值,根据题目特点,将一个代数式的值整体代入,求值时方便又快捷,这种整体代入的方法经常用到.
5.(2014·宜春模拟)已知a=b-2,则(a-b)2+(b-a)+1的值为 .
【解析】因为a=b-2,所以a-b=-2,b-a=2,
所以原式=(-2)2+2+1=7.
答案:7
6.已知=3,求代数式-的值.
【解析】因为=3,所以=.
所以-
=2×-×
=2×3-×
=6-
=.
求代数式的值的应用
1.某种导火线的燃烧速度是0. ( http: / / www.21cnjy.com )81cm/s,爆破员跑开的速度是5m/s,为在点火后使爆破员跑到150m以外的安全地区,导火线的长度可以为 ( )
A.22cm B.23cm
C.24cm D.25cm
【解析】选D.导火线的长度是与安全地区的路程相关,设点火后使爆破员跑到xm以外的安全地区,那么所需导火线的长度至少为×0.81cm.当x=150时,导火线的长度为×0.81=24.3(cm),故导火线的长度至少为24.3cm,只有D项符合要求.
2.(2013·苏州中考)按照如图所示的操作步骤,若输入x的值为2,则输出的值为 .
【解题指南】解答本题的两个步骤
(1)按运算程序列出代数式.
(2)把x的值代入所列的代数式.
【解析】由图可知输出的结果为(x+3)2-5,
当x=2时,(x+3)2-5=(2+3)2-5=25-5=20.
答案:20
3.(2013·红河州中考)下列图形是 ( http: / / www.21cnjy.com )由一些小正方形和实心圆按一定规律排列而成的,如图所示,按此规律排列下去,第20个图形中有 个实心圆.
( http: / / www.21cnjy.com )
【解析】第(1)个图形中有4+2×0=4个实心圆;
第(2)个图形中有4+2×1=6个实心圆;
第(3)个图形中有4+2×2=8个实心圆;…,
第(n)个图形中有4+2×(n -1)个实心圆;
所以第20个图形中有4+2×19=42个实心圆.
答案:42
4.若梯形的上底为a,下底为b,高为h,则梯形面积为 ,当a=2cm,
b=4 cm,h=3cm时,梯形的面积为 .
【解析】梯形的面积公式为S=(上底+下底)×高÷2,
即S=(a+b)h,
当a=2cm,b=4cm,h=3cm时,
S=×(2+4)×3=×6×3=9(cm2).
答案:(a+b)h 9cm2
5.一块三角尺的形状和尺寸如图所示,a为直角边的长,r为圆孔的半径.
(1)求阴影部分的面积S.
(2)当a=8cm,r=1.5cm时.求S的值(π取3.14).
( http: / / www.21cnjy.com )
【解析】(1)因为三角形的面积为a2,
圆的面积为πr2,
所以阴影部分的面积S=a2-πr2.
(2)当a=8cm,r=1.5cm,π取3.14时,
S=a2-πr2=×82-3.14×1.52
=32-7.065=24.935(cm2).
【错在哪?】作业错例 课堂实拍
已知a=,b=,求代数式a+2b的值.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:
答案:(1)① (2)
复习题训练及解析(三)
单项式
1.在x2-x,2πx3y,,-4,a中单项式的个数是 ( )
A.1 B.2 C.3 D.4
【解析】选C.所给式子中,单项式有2πx3y,-4,a,共3个.
【易错提醒】不是单项式,凡是分母中有字母的代数式都不是单项式.
2.(2013·德宏州中考)-4a2b的次数是 ( )
A.3 B.2 C.4 D.-4
【解析】选A.因为单项式-4a2b中所有字母指数的和为2+1=3,所以此单项式的次数为3.
3.(2013·岳阳中考)单项式-5x2y的系数是 .
【解析】因为-5x2y=-5·x2y,所以该单项式的系数是-5.
答案:-5
【变式训练】(2014·椒江区二模)单项式-2πy的系数为 ( )
A.-2π B.-2 C.2 D.2π
【解析】选A.因为-2πy=-2π·y,
所以-2πy的系数为-2π.
4.(2013·淮安中考)观察一列单项式:x,3x2,5x3,7x,9x2,11x3,…,则第2013个单项式是 .
【解题指南】解答本题的两个关键
(1)知道系数是连续的奇数.
(2)知道指数是按1,2,3的顺序三个一循环.
【解析】本题这一列单项式的系数是1,3,5 ( http: / / www.21cnjy.com ),7,9,…,是连续的奇数,可用2n-1表示.所以第2013个单项式的系数为2×2013-1=4025.字母x的指数是1,2,3,1,2,3,…,三个一循环,2013÷3=671,所以指数为3.所以第2013个单项式是4025x3.
答案:4025x3
5.已知-2xmyn+1的次数为2,求3m+3n-5的值.
【解析】因为-2xmyn+1的次数为2,所以m+n+1=2.
所以m+n=1(向所求方向进行转化).
所以3m+3n=3,所以3m+3n-5=3-5=-2.
【变式训练】如果(m+1)2x2yn+1是关于x,y的六次单项式,求m,n的值.
【解析】因为(m+1)2x2yn+1是关于x,y的六次单项式,
所以2+n+1=6,而m+1≠0,解得m≠-1,n=3.
多项式
1.多项式-πx2y+22xy-1是 ( )
A.五次三项式 B.四次三项式
C.二次三项式 D.三次三项式
【解析】选D.多项式-πx2y+22xy-1是三次三项式.
【易错提醒】本题要注意两个问题
(1)π不是字母,所以第一项-πx2y的次数是3次,不是4次.
(2)单项式的次数是所有字母的指数和,而不是所有指数的和,所以第二项22xy的次数是2次,不是4次.
【变式训练】下列多项式是二次三项式的是 ( )
A.2x2+3 B.3x2+2
C.2x+3y+1 D.2x2+3y+1
【解析】选D.选项A,B是二次二项式,选项C是一次三项式,选项D是二次三项式.
2.(2013·佛山中考)多项式1+2xy-3xy2的次数及最高次项的系数分别
是 ( )
A.3,-3 B.2,-3 C.5,-3 D.2,3
【解析】选A.因为多项式的次数就是多项式中次数最高项的次数,所以1+2xy-3xy2的次数是3,这一项的系数是-3.
3.(2013·济宁中考)如果整式xn-2-5x+2是关于x的三次三项式,那么n等于
( )
A.3 B.4 C.5 D.6
【解析】选C.由多项式次数的概念,整式xn-2-5x+2是关于x的三次三项式,所以n-2=3,n=5.
4.(2014·赤峰期中检测)多项式-x2+2x+3xyz是 次 项式.
【解析】多项式-x2+2x+3xyz有三项,最高次项的次数是3,所以该多项式是三次三项式.
答案:三 三
5.如果2xm+1+3x+1是关于x的三次多项式,求m的值.
【解析】因为2xm+1+3x+1是关于x的三次多项式,所以x的最高次数是3,即m+1=3.
解得m=2.
升幂排列与降幂排列
1.把多项式2x2+3x3-x+5x4-1按字母x降幂排列是 ( )
A.2x2+3x3-x+5x4-1 B.5x4+3x3+2x2-1-x
C.-1-x+2x2+3x3+5x4 D.5x4+3x3+2x2-x-1
【解析】选D.多项式2x2+ ( http: / / www.21cnjy.com )3x3-x+5x4-1的各项是2x2,3x3,-x,5x4,-1,所以按字母x降幂排列为5x4+3x3+2x2-x-1.
2.对于多项式22m2+3m-1,下列说法正确的是 ( )
A.它是关于m的四次三项式
B.它的常数项是1
C.它是按m的降幂排列
D.它是按m的升幂排列
【解析】选C.多项式22m2+3m-1 ( http: / / www.21cnjy.com )的各项的次数分别为2,1,0.由于多项式的次数是“多项式中次数最高的项的次数”,所以多项式22m2+3m-1的次数是2,因此A不正确.它的常数项是-1,选项B不正确.
在多项式22m2+3m-1中,22m2的次数是2,3m的次数是1,因此是按m的降幂排列,选项C正确,D不正确.
3.把多项式-2x+1-x3+x2按字母x的降幂排列为 .
【解析】-2x+1-x3+x2按字母x的降幂排列为-x3+x2-2x+1.
答案:-x3+x2-2x+1
4.把多项式4a3b-3ab2+a4-5b5按字母b的升幂排列是 .
【解析】把多项式4a3b-3ab2+a4-5b5按b的升幂排列为a4+4a3b-3ab2-5b5.
答案:a4+4a3b-3ab2-5b5
【互动探究】如果是按字母a的降幂排列,结果应该是什么 与按b的升幂排列的结果有什么关系
【解析】把多项式4a3b-3ab2+a4-5b5按字母a的降幂排列为a4+4a3b-3ab2-5b5,与按b的升幂排列的结果一样.
5.将多项式5a2b5+ab-3a3b3-6a4b2+1按要求排列:
(1)按字母a降幂排列.
(2)按字母b升幂排列.
【解析】(1)按字母a降幂排列为-6a4b2-3a3b3+5a2b5+ab+1.
(2)按字母b升幂排列为1+ab-6a4b2-3a3b3+5a2b5.
【错在哪?】作业错例 课堂实拍
把下列多项式按字母x先进行降幂排列,再进行升幂排列.
12x-10x2+8.
( http: / / www.21cnjy.com )
(1)找错:出现错误的是 .
(2)纠错:
答案:(1)①②
(2)①是-10x2+12x+8,②是8+12x-10x2.
复习题训练及解析(四)
同类项的概念及应用
1.(2014·太原期末模拟)下列各式中,与x2y是同类项的是 ( )
A.xy2 B.x2+y C.-x2y D.3x2y2
【解析】选C. xy2和3x2y2与x2y中相同字母的指数不相同;x2+y是多项式,所以A,B,D均不是x2y的同类项.
2.下列各组中的两项不是同类项的是 ( )
A.-25mn和3nm B.7.2a2b和a2b
C.2x3y2和-3x2y3 D.-125和93
【解析】选C.因为2x3y2和-3x2y3的相同字母的指数不同,所以不是同类项.
【易错提醒】同类项中的指数相同,指的是 ( http: / / www.21cnjy.com )相同字母的指数相同,而不是常数的指数,所以2x3y2和-3x2y3不是同类项,-125和93是同类项.
【变式训练】下列各组中的两项是同类项的是 ( )
A.m3n4和m4n3 B.ab与ab
C.m3与a3 D.2x与2y
【解析】选B.m3n4和m4n3相同字母的指数不同,不是同类项;m3与a3字母不同,不是同类项;2x与2y字母不同,不是同类项.
3.若3xmy3与-x2yn是同类项,则(-m)n等于 ( )
A.6 B.-6 C.8 D.-8
【解题指南】解答本题的两个步骤
(1)根据同类项的定义求出m,n的值.
(2)代入(-m)n计算.
【解析】选D.因为3xmy3与-x2yn是同类项,所以m=2,n=3,所以(-m)n=(-2)3=-8.
4.(2013·凉山州中考)如果单项式-xa+1y3与ybx2是同类项,那么a,b的值分别为
( )
A.a=2,b=3 B.a=1,b=2
C.a=1,b=3 D.a=2,b=2
【解析】选C.因为-xa+1y3与ybx2是同类项,所以a+1=2,b=3,所以a=1,b=3.
5.写出3a2的一个同类项: .
【解析】答案不唯一,只要只含字母a,且a的指数是2,都是3a2的一个同类项,如-2a2.
答案:-2a2(答案不唯一)
6.(2014·松原实验期末检测)当a= 时,5xa-1y2与-3x2y2是同类项.
【解析】由题意得a-1=2,所以a=3.
答案:3
7.如果单项式5xmy4与单项式xy2n是同类项,那么m= ,n= .
【解析】根据同类项的条件:m=1,4=2n,即n=2.
答案:1 2
【变式训练】已知代数式2a3bn+1与-3am-2b2是同类项,则2m+3n= .
【解析】由同类项的定义,可知m-2=3,n+1=2,
解得m=5,n=1,则2m+3n=13.
答案:13
8.判断下列各组式子是不是同类项:
(1)22ab3与-3ab3. (2)0.2abc与7ac.
(3)-5x2y3与4x3y2. (4)π与10.
【解析】(1)是同类项.(2)不是同类项.(3)不是同类项.(4)是同类项.
【易错提醒】常数项都是同类项,要注意π是常数,本题中的π和10是同类项.
9.若3ambn-1与-a4b2是同类项,求(n-m)2014的值.
【解析】由同类项的概念得m=4,2=n-1,
则:m=4,n=3.
所以(n-m)2014=(3-4)2014=(-1)2014=1.
【错在哪?】作业错例 课堂实拍
多项式3x2y-3+5x2y+2xy2+5有哪几项 其中哪些是同类项
( http: / / www.21cnjy.com )
(1)找错:出现错误的是 .
(2)纠错: .
答案:(1)②
(2) 3x2y,+5x2y是同类项
复习题训练及解析(五)
合并同类项
1.(2013·梧州中考)化简a+a= ( )
A.2 B.a2 C.2a2 D.2a
【解析】选D.根据合并同类项的法则:系数相加减,字母及字母的指数不变,可得a+a=2a.
【变式训练】(2014·廊坊一模)计算a+2a= ( )
A.2a2 B.3a2
C.a(1+a) D.3a
【解析】选D.a+2a=(1+2)a=3a.
2.(2013·苏州中考)计算-2x2+3x2的结果为 ( )
A.-5x2 B.5x2 C.-x2 D.x2
【解析】选D.原式=(-2+3)x2=x2.
【变式训练】下列计算中,正确的是 ( )
A.-a-a=0 B.3a+2a=5a2
C.a3+a3=a6 D.a2+a2=2a2
【解析】选D.-a-a=-2a,3a+2a=5a,a3+a3=2a3,a2+a2=2a2.
3.若代数式ax+bx合并同类项后结果为零,则a,b满足的关系式为 ( )
A.a+b=1 B.a=b C.a-b=0 D.a+b=0
【解析】选D.ax+bx=(a+b)x=0,所以a+b=0.
【知识归纳】代数式值恒为0的条件
(1)一个代数式的值恒为0,并不是代数式中的所有字母均为0,而是指代数式中的字母无论取何值,其值均为0.
(2)如果代数式的值恒为0,那么其合并后的系数一定是0.
4.若单项式-5xm-1y2与4x3yn-1能够合并,则m-n= .
【解析】根据题意得单项式-5xm-1y2与4x3yn-1是同类项,
所以m-1=3,n-1=2,
解得m=4,n=3,则m-n=4-3=1.
答案:1
5.合并同类项:
(1)4a2+3b2-2ab-3a2-5b2.
(2)3xy2-5xy+0.5x2y-3xy2-4.5x2y.
【解析】(1)原式=(4a2-3a2)+(3b2-5b2)-2ab=a2-2b2-2ab.
(2)原式=(3xy2+0.5x2y-3xy2-4.5x2y)-5xy=-4x2y-5xy.
【变式训练】如果把x-y看作一个因式,那么代数式2(x-y)2-(x-y)+3(x-y)2-4(x-y)合并后的结果是什么
【解析】2(x-y)2-(x-y)+3(x-y)2-4(x-y)
=5(x-y)2-5(x-y).
6.求多项式5x2+4-3x2-5x-2x2-5+6x的值,其中x=-3.
【解析】5x2+4-3x2-5x-2x2-5+6x
=5x2-3x2-2x2-5x+6x+4-5
=(5-3-2)x2+(-5+6)x+(4-5)
=x-1.
当x=-3时,原式=-3-1=-4.
合并同类项的应用
1.如图,阴影部分的面积是 ( )
( http: / / www.21cnjy.com )
A.xy B.xy C.5xy D.2xy
【解题指南】解答图形面积问题的基本方法
(1)转化:把不规则图形的面积转化为规则图形的面积的和或差.
(2)计算:由规则图形的面积表示出不规则图形的面积.
【解析】选A.阴影部分面积为:3x×2y-0.5x×y-×x×2y=6xy-xy-xy=xy.
2.若a<0,则2014a-10|a|等于 ( )
A.2004a B.-2024a
C.2024a D.-2014a
【解析】选C.2014a-10|a|=2014a+10a=2024a.
3.已知A等于2xy,B是A的3倍,C是B的,那么A+B+C= .
【解析】由题意知B=3×2xy=6xy,C=×6xy=4xy,
所以A+B+C=2xy+6xy+4xy=12xy.
答案:12xy
4.某仓库原有货物mt,上午运进8车货物,下午运出3车货物,后来又运进2车货物,如果每车载货at,那么仓库中现有货物 t.
【解析】仓库中现有货物m+8a-3a+2a=(m+7a)t.
答案:(m+7a)
5.七年级一班为建立“图书角”,各组同学 ( http: / / www.21cnjy.com )踊跃捐书.一组捐x本书,二组捐的书是一组的2倍还多2本,三组捐的书是一组的3倍少1本,则三个小组共捐书
本.
【解析】由题意知,二组捐了(2x+2)本,三组捐了(3x-1)本,所以三个小组共捐书:
x+2x+2+3x-1=(6x+1)(本).
答案:(6x+1)
6.(2014·晋中模拟)要使代数式a3+2ma2-5a2+1中不含有a2的项,则m= .
【解析】由已知要使代数式a3+2ma2-5a2+1中不含有a2的项,可得2m-5=0,即m=.
答案:
7.我校七年级(1)班三个兴趣小组为灾区捐款 ( http: / / www.21cnjy.com ),舞蹈小组的同学共捐款x元,美术小组的同学捐款比舞蹈小组捐款的2倍还多8元,篮球小组的同学捐款比美术小组捐款的一半少6元,这三个小组的同学一共捐款多少元
【解析】由题意知,美术小组的同学捐款为(2x+8)元,篮球小组的同学捐款为元,三个小组同学的捐款数为:x+(2x+8)+
=x+2x+8+x+4-6=(4x+6)元.
【错在哪?】作业错例 课堂实拍
合并同类项5y-2x2y-3y+3x2y.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错: .
答案:(1)②
(2)原式=2y+x2y
复习题训练及解析(六)
去括号法则及应用
1.(2014·南昌模拟)去括号-(a-b)结果正确的是 ( )
A.a-b B.a+b C.-a-b D.b-a
【解析】选D.-(a-b)=-a+b=b-a.
【易错提醒】括号前是“-”号,括号里各项都改变符号,本题易错选C.
2.下列代数式中,去括号的结果等于a-b-c的是 ( )
A.-(a+b+c) B.-b-(c-a)
C.a-(b-c) D.-c+(b-a)
【解析】选B.-(a+b+c)=-a-b-c;-b-(c-a)=-b-c+a=a-b-c;a-(b-c)=a-b+c;
-c+(b-a)=-c+b-a=-a+b-c.
【变式训练】下面去括号错误的是 ( )
A.3(a-b)=3a-b B.a+(b-c)=a+b-c
C.a-(b+c)=a-b-c D.-(a-2b)=-a+2b
【解析】选A.3(a-b)=3a-3b.
3.下列运算正确的是 ( )
A.-2(3x-1)=-6x-1
B.-2(3x-1)=-6x+1
C.-2(3x-1)=-6x-2
D.-2(3x-1)=-6x+2
【解析】选D.-2(3x-1)=-6x+2,所以A,B,C选项错误.
【知识归纳】去括号时,括号前有负数相 ( http: / / www.21cnjy.com )乘,可以运用去括号法则将括号内的项都改变符号,再与负数的绝对值相乘;也可以直接运用乘法分配律将负数与括号内各项相乘,注意不能漏乘.
4.(2013·上海中考)计算:2(a-b)+3b= .
【解析】2(a-b)+3b=2a-2b+3b=2a+b.
答案:2a+b
5.(2013·厦门中考)计算:5a+2b+(3a—2b).
【解析】5a+2b+(3a—2b)=5a+2b+3a—2b
=8a.
6.先化简,再求值:3a2-[7a2-2a-3(a2-a)+1],其中a=-1.
【解析】3a2-[7a2-2a-3(a2-a)+1]
=3a2-(7a2-2a-3a2+3a+1)
=3a2-(4a2+a+1)
=3a2-4a2-a-1
=-a2-a-1.
当a=-1时,原式=-(-1)2-(-1)-1=-1.
添括号法则及应用
1.下列等式:(1)-a-b=-(a-b).(2)-a+b=-(-b+a).(3)4-3x=-(3x-4).其中一定成立的等式的个数是 ( )
A.0个 B.1个 C.2个 D.3个
【解析】选C.因为-a-b=-(a+b),-a+b=-(-b+a),4-3x=-(3x-4),所以一定成立的等式有2个.
【知识拓展】添括号与去括号的关系
(1)添括号与去括号是两个互逆的过程.
(2)添括号是否正确,可通过去括号进行验证.
2.不改变3a2-2b2-b+a+ab的 ( http: / / www.21cnjy.com )值,把二次项放在前面有“+”号的括号里,一次项放在前面有“-”号的括号里,下列各式正确的是 ( )
A.+(3a2+2b2+ab)-(b+a)
B.+(-3a2-2b2-ab)-(b-a)
C.+(3a2-2b2+ab)-(b-a)
D.+(3a2-2b2+ab)-(b+a)
【解析】选C.3a2-2b2-b+a+ab=3a2-2b2+ab-b+a
=+(3a2-2b2+ab)-(b-a).
3.已知a-b=1,则代数式3-2a+2b的值是 ( )
A.-1 B.1 C.-5 D.5
【解析】选B.3-2a+2b=3-2(a-b)=3-2×1=1.
【一题多解】选B.本题也可用下面的方法求解,由a-b=1,得a=b+1,代入可得3-2a+2b=3-2(b+1)+2b
=3-2b-2+2b=1.
4.(2014·宿州质检)若2a-b=1,则4a-2b-1= .
【解析】4a-2b-1=2(2a-b)-1=2×1-1=1.
答案:1
5.a3+3a2-2a=a3+( ),
a-4-2b-c=(a-2b)-( ).
【解析】a3+3a2-2a=a3+(3a2-2a),
a-4-2b-c=(a-2b)-(c+4).
答案:3a2-2a c+4
6.按要求把多项式x3-5x2-4x+9添上括号.
(1)把它放在前面带有“+”号的括号里.
(2)把它放在前面带有“-”号的括号里.
(3)把后两项放在前面带有“-”号的括号里.
(4)把后三项放在前面带有“-”号的括号里.
【解析】(1)x3-5x2-4x+9=+(x3-5x2-4x+9).
(2)x3-5x2-4x+9
=-(-x3+5x2+4x-9).
(3)x3-5x2-4x+9=x3-5x2-(4x-9).
(4)x3-5x2-4x+9=x3-(5x2+4x-9).
【错在哪?】作业错例 课堂实拍
先去括号,再合并同类项:
-(2a2+5)-(3a2-2)-2(-4a2-1).
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:原式 .
答案:(1)①
(2) =-2a2-5-3a2+2+8a2+2=(-2-3+8)a2+(2+2-5)=3a2-1
复习题训练及解析(七)
整式的加减运算
1.已知有一整式与(2x2+5x-2)的和为(2x2+5x+4),则此整式为 ( )
A.2 B.6
C.10x+6 D.4x2+10x+2
【解析】选B.此整式为(2x2+5x+4)-(2x2+5x-2)=2x2+5x+4-2x2-5x+2=6.
【易错提醒】本题要理清三个整式之间的关系,避免出现这个数等于(2x2+5x+4)+(2x2+5x-2)这样的错误.
【变式训练】比多项式5a2-2a-3ab少5a2-2ab的多项式是 ( )
A.-2a-ab B.-2a-5ab
C.-2a+5ab D.2a+ab
【解析】选A.5a2-2a-3ab-(5a2-2ab)=5a2-2a-3ab
-5a2+2ab=-2a-ab.
2.一个多项式减去x2-2y2等于x2+y2,则这个多项式是 ( )
A.-2x2+y2 B.2x2-y2
C.x2-2y2 D.-x2+2y2
【解析】选B.这个多项式是(x2-2y2)+(x2+y2)=2x2-y2.
【互动探究】这两个多项式的和是多少
【解析】这两个多项式的和是(2x2-y2)+(x2-2y2)=3x2-3y2.
3.若M和N都是3次多项式,则M+N为 ( )
A.3次多项式 B.6次多项式
C.次数不超过3的整式 D.次数不低于3的整式
【解析】选C.因为M和N都是3次多项式,
所以M+N为次数不超过3的整式.
4.设a=x2+x,b=x-2,则a与b的大小关系为 .
【解析】由题意得a-b=x2+x-(x-2)=x2+2>0,
所以a>b.
答案:a>b
【知识拓展】作差法比较两个整式的大小
比较两个整式的大小,用作差法, ( http: / / www.21cnjy.com )如果差大于0,则被减数大于减数,如果差小于0,则被减数小于减数.例如,若A=a+b,B=a-b,则A与B的大小关系如何 因为A-B=a+b-(a-b)=a+b-a+b=2b,所以当b<0时,A
5.已知多项式A=3x2-6x+5,B=2x2+7x-6,求2A-3B.
【解析】因为A=3x2-6x+5,B=2x2+7x-6,
所以2A-3B=2(3x2-6x+5)-3(2x2+7x-6)
=6x2-12x+10-6x2-21x+18=-33x+28.
6.化简求值:
3a2+(4a2-2a-1)-2(3a2-a+1),其中a=.
【解析】3a2+(4a2-2a-1)-2(3a2-a+1)
=3a2+4a2-2a-1-6a2+2a-2=a2-3.
当a=时,原式=()2-3=-3=-.
【变式训练】(2014·广州一模)先化简,再求值4(x-y)-2(3x+y)+1,其中x=1,y=-.
【解析】原式=4x-4y-6x-2y+1
=-2x-6y+1,
当x=1,y=-时,原式=-2×1-6×+1
=-2+2+1=1.
整式加减的实际应用
1.长方形一边等于3a-2b,另一边比它小a-b,则此长方形另一边的长等于
( )
A.4a-3b B.4a+b C.2a+b D.2a-b
【解析】选D.根据题意得:(3a-2b)-(a-b)=3a-2b-a+b=2a-b.
2.(2013·聊城中考)把地球看成 ( http: / / www.21cnjy.com )一个表面光滑的球体,假设沿地球赤道绕紧一圈钢丝,然后把钢丝加长,使钢丝圈沿赤道处处高出球面16cm,那么钢丝大约需要加长 ( )
A.102cm B.104cm C.106cm D.108cm
【解题指南】解答本题考查的知识及解题关键
(1)此题主要考查了圆的周长公式以及科学记数法.
(2)根据已知得出图形变化前后的周长是解题关键.
【解析】选A.设地球半径为rcm,
则地球的周长为2πrcm,
假设沿地球赤道绕紧一圈钢丝,然后把钢丝加长,使钢丝圈沿赤道处处高出球面16cm,
故此时钢丝围成的圆形的周长变为2π(r+16)cm,
所以钢丝大约需要加长:2π(r+16)-2πr≈100(cm)=102(cm).
3.一个长方形的相邻两边长分别为3m+2n和m+n,则这个长方形的周长为 .
【解析】这个长方形的周长为2(3m+2n+m+n)
=2(4m+3n)=8m+6n.
答案:8m+6n
4.已知三角形的第一边长为3a+2b,第二边比第一边长a-b,第三边比第二边短2a,求这个三角形的周长.
【解析】第一边长为3a+2b,
则第二边长为(3a+2b)+(a-b)=4a+b,
第三边长为(4a+b)-2a=2a+b,
所以这个三角形的周长为(3a+2b)+(4a+b)+(2a+b)=3a+2b+4a+b+2a+b=9a+4b.
5.一公园的成年人票价是15元,儿童买 ( http: / / www.21cnjy.com )半票,甲旅行团有x(名)成年人和y(名)儿童;乙旅行团的成年人数是甲旅行团成年人数的2倍,儿童数比甲旅行团儿童人数的2倍少8人,这两个旅行团的门票费用总和是多少
【解析】甲旅行团的门票费用:(15x+y)元,
乙旅行团的门票费用:[15×2x+(2y-8)]元,
所以(15x+y)+[15×2x+(2y-8)]
=15x+y+30x+15y-60=(45x+y-60)元.
即这两个旅行团的门票费用总和是元.
【错在哪?】作业错例 课堂实拍
求a2b-[a2b-2(3abc-a2c)-4a2c]-3abc的值,其中a=-1,b=-3,c=.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:原式
答案:(1)①
(2)
=-a2b+2a2c+3abc.
当a=-1,b=-3,c=时,
原式=-(-1)2×(-3)+2×(-1)2×+3×(-1)×(-3)×=3+1+
=8
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
