数学七上第4章图形的初步认识复习题及解析
文档属性
| 名称 | 数学七上第4章图形的初步认识复习题及解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-20 00:00:00 | ||
图片预览



文档简介
复习题训练及解析(一)
常见的几何体
1.在六角螺母、哈密瓜、易拉罐、足球、字典中,物体的形状类似于棱柱的个数是 ( )
A.0 B.1 C.2 D.3
【解析】选C.六角螺母、字典都有上、下两个底面,并且底面都是多边形,因此它们都类似于棱柱.故选C.
2.(2014·乐山实验月考)下面几何图形中,是棱柱的是 ( )
( http: / / www.21cnjy.com )
【解题指南】判断棱柱的两个关键点
(1)由上下两个底面以及侧面组成.
(2)上下两个底面是完全相同的多边形,侧面是四边形.
【解析】选B.棱柱的侧面应是四边形,符合这个条件的只有选项B中的几何体.
【知识拓展】棱柱的性质
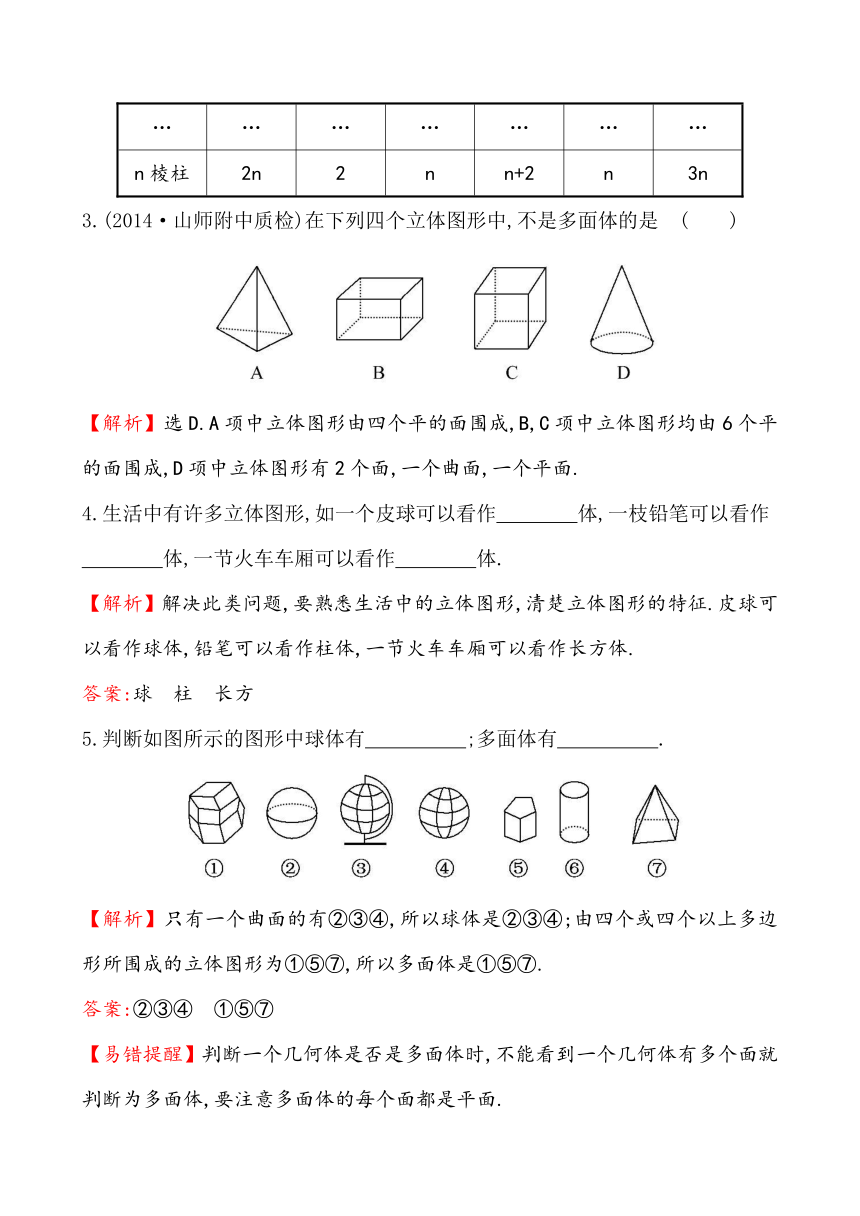
区别名称 顶点数 底面数 侧面数 总面数 侧棱数 总棱数
三棱柱 6 2 3 5 3 9
四棱柱 8 2 4 6 4 12
五棱柱 10 2 5 7 5 15
六棱柱 12 2 6 8 6 18
… … … … … … …
n棱柱 2n 2 n n+2 n 3n
3.(2014·山师附中质检)在下列四个立体图形中,不是多面体的是 ( )
( http: / / www.21cnjy.com )
【解析】选D.A项中立体图形由四个平的面围成,B,C项中立体图形均由6个平的面围成,D项中立体图形有2个面,一个曲面,一个平面.
4.生活中有许多立体图形,如一个皮球可以看作 体,一枝铅笔可以看作
体,一节火车车厢可以看作 体.
【解析】解决此类问题,要熟悉生活中的立体图形,清楚立体图形的特征.皮球可以看作球体,铅笔可以看作柱体,一节火车车厢可以看作长方体.
答案:球 柱 长方
5.判断如图所示的图形中球体有 ;多面体有 .
( http: / / www.21cnjy.com )
【解析】只有一个曲面的有②③④,所以球体是②③④;由四个或四个以上多边形所围成的立体图形为①⑤⑦,所以多面体是①⑤⑦.
答案:②③④ ①⑤⑦
【易错提醒】判断一个几何体是否是多面体时,不能看到一个几何体有多个面就判断为多面体,要注意多面体的每个面都是平面.
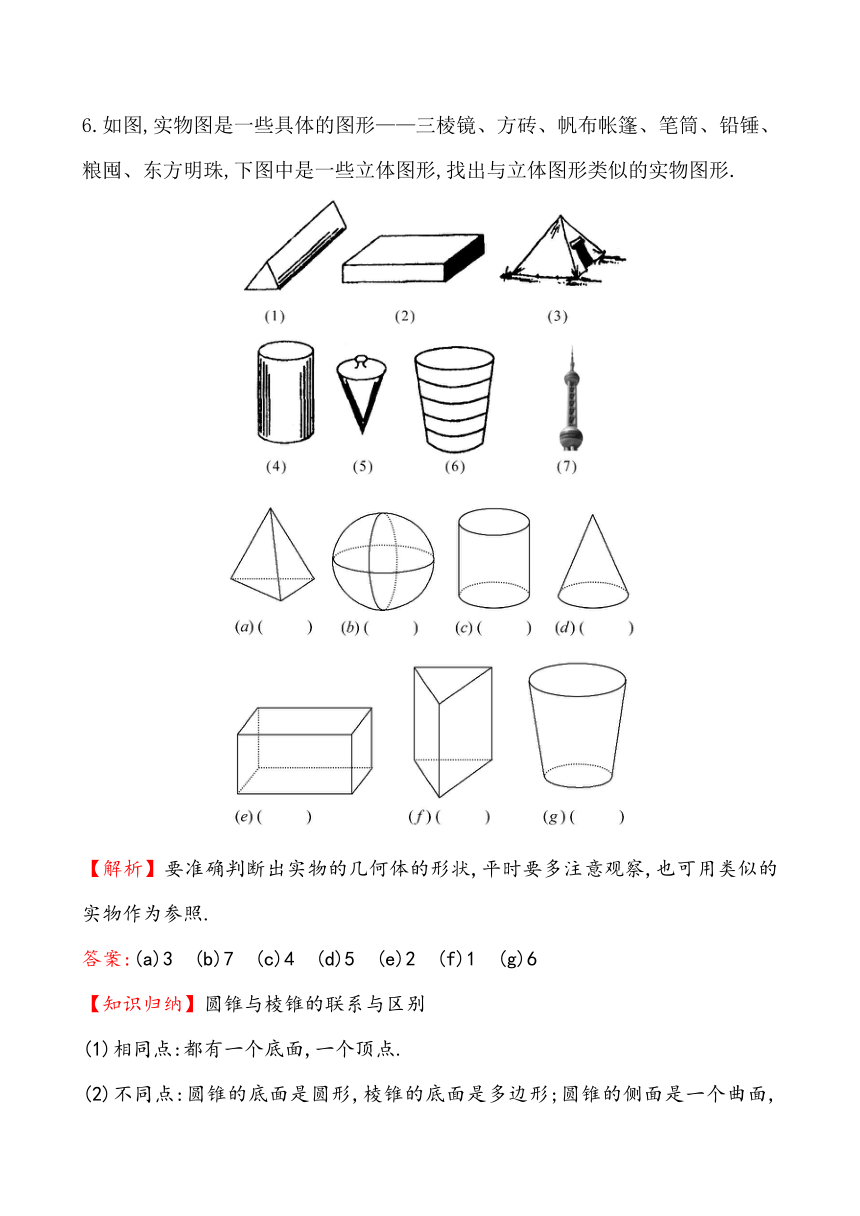
6.如图,实物图是一些具体的图形——三棱 ( http: / / www.21cnjy.com )镜、方砖、帆布帐篷、笔筒、铅锤、粮囤、东方明珠,下图中是一些立体图形,找出与立体图形类似的实物图形.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
【解析】要准确判断出实物的几何体的形状,平时要多注意观察,也可用类似的实物作为参照.
答案:(a)3 (b)7 (c)4 (d)5 (e)2 (f)1 (g)6
【知识归纳】圆锥与棱锥的联系与区别
(1)相同点:都有一个底面,一个顶点.
(2)不同点:圆锥的底面是圆形,棱锥的底面是多边形;圆锥的侧面是一个曲面,棱锥的侧面是由几个平面围成的,且每个平面都是三角形.
7.请你把相应的实物与图形用线连结起来.
( http: / / www.21cnjy.com )
答案:
( http: / / www.21cnjy.com )
【错在哪?】作业错例 课堂实拍
填空:判断下列实物类似于哪一种几何体.
(1)数学课本是 .
(2)粉笔是 .
( http: / / www.21cnjy.com )
(1)找错:上面解析过程 (填“有”或“无”)错误.
(2)纠错: .
答案: (1)有 (2)数学课本的形状是长方体,粉笔的侧面是曲面,两个底面是两个大小不相等的圆,是圆台.
答案:(1)长方体 (2)圆台
复习题训练及解析(二)
由立体图形到三视图
1.(2013·盐城中考)下面的几何体中,主视图不是长方形的是 ( )
( http: / / www.21cnjy.com )
【解析】选C.选项A,B,D图形的主视图是矩形,只有选项C图形的主视图是等腰梯形.
2.(2013·湛江中考)如图是由6个大小相同的正方体组成的几何体,它的左视图是 ( )
( http: / / www.21cnjy.com )
【解析】选A.从左边看,左边一列有两个正方形,右边有一个.
3.(2013·衡阳中考)下列几何体,同一个几何体的主视图与俯视图不同的是
( )
( http: / / www.21cnjy.com )
【解析】选C.图中圆柱的主视图和俯视图都是 ( http: / / www.21cnjy.com )长方形;正方体的正视图和俯视图都是正方形;球的正视图和俯视图都是圆;圆锥的正视图是三角形,俯视图是圆,故选C.
【知识拓展】常见几何体的三视图
几何体视图
主视图
左视图
俯视图
4.(2013·广州中考)如图所示的几何体的主视图是 ( )
( http: / / www.21cnjy.com )
【解析】选A.因为选项B是两个矩形,中间有分隔线,显然不是主视图,而选项C是这个图形的俯视图,选项D不是三视图,
所以确定主视图为选项A.
5.(2013·潍坊中考)如图是常用的一种圆顶螺杆,它的俯视图正确的是 ( )
( http: / / www.21cnjy.com )
【解析】选B.因为圆柱俯视图是一个圆,大圆与小圆组合在一起,所以这个组合体的俯视图是B选项中的图形.
6.已知由四个大小相同的小正方体搭成的几何体如图所示,请画出该几何体的三视图.
( http: / / www.21cnjy.com )
【解析】从正面看有2列,左列有2个正方形,右列有1个正方形;
从左面看有2列,左列有2个正方形,右列有1个正方形;
从上面看也有2列,左列有1个正方形,右列有2个正方形.如图所示:
( http: / / www.21cnjy.com )
由三视图到立体图形
1.某几何体的三视图如图所示,则这个几何体是 ( )
( http: / / www.21cnjy.com )
A.圆柱 B.正方体
C.球 D.圆锥
【解析】选D.根据主视图和左视图为三角形判断出是锥体,根据俯视图是圆形及圆心可判断出这个几何体是圆锥.
【知识归纳】几何体与三视图的联系
已知一个立体图形,可以画出它的三视图,由三 ( http: / / www.21cnjy.com )视图也可以画出几何体.先根据主视图和左视图可以确定几何体是柱体还是锥体,再依据俯视图确定是棱体还是圆体;两方面结合可以确定这个几何体.
2.(2013·内江中考)一个几何体的三视图如图所示,那么这个几何体是 ( )
( http: / / www.21cnjy.com )
【解析】选C.从俯视图看, ( http: / / www.21cnjy.com )它是一个三角形,而选项A和B的俯视图是圆,不可能出现三角形,所以排除A,B,从左视图看,它是一个长方形,而选项D的左视图是三角形,不可能出现长方形,所以排除D,只有选项C符合题意.
3.图中三视图所对应的几何体是 ( )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
【解析】选C.从主视图可以排除选项A,B,从俯视图排除选项D,故选C.
4.一个立体图形的三视图是三个圆,则这个图形是 .
【解析】球体的三视图都是圆,这个图形是球体.
答案:球体
【错在哪?】作业错例 课堂实拍
画出下列几何体的三视图.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)找错:上面解析过程 (填“有”或“无”)错误.
(2)纠错:
答案:(1)有
(2)
( http: / / www.21cnjy.com )
复习题训练及解析(三)
立体图形与平面图形的转化
1.(2013·恩施中考)如图,下列四个选项中,不是正方体表面展开图的是
( )
( http: / / www.21cnjy.com )
【解析】选C.选项A,B,D都可以折叠成一个正方体,只有选项C不能折叠成正方体,因此,选项C不是正方体的表面展开图,所以,本题应选C.
【知识拓展】正方体表面展开图(一四一型6种)口诀:中间四个一连串,两边各一随便放.
( http: / / www.21cnjy.com )
(二三一或一三二型3种)口诀:二三紧连挪一个,三一相连一随便.
( http: / / www.21cnjy.com )
(二二二型1种)口诀:两两相连各挪一.
( http: / / www.21cnjy.com )
(三三型1种)口诀:三个两排一对齐.
( http: / / www.21cnjy.com )
2.(2013·河南中考)如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是 ( )
A.1 B.4 C.5 D.6
【解析】选B.由展开图可知正方体的相对面分别为:1与6相对,2与4相对,3与5相对.
3.如图所示的平面图形中,不可能围成圆锥的是 ( )
( http: / / www.21cnjy.com )
【解析】选D.展开想象,把平面图形折叠成体,检查折叠成的立体图形是否为圆锥.
【归纳整合】圆柱、圆锥的表面展开图
圆柱的表面展开图是由两个相同的圆形和一个矩形组成的,圆锥的表面展开图是由一个圆形和一个扇形组成的.
4.(2013·南京中考)如图,一个几 ( http: / / www.21cnjy.com )何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是 ( )
( http: / / www.21cnjy.com )
【解题指南】观察带颜色的小正方形所在的位置排除A,C选项,再根据正方体表面展开图的特点排除D.
【解析】选B.通过观察涂黑正方形一 ( http: / / www.21cnjy.com )面接着一个三角形,三面接着三个正方形,A,C答案均不直接和三角形相接,D选项不能围成密封的几何体,所以不选,只有B选项符合.
5.若要使得图中的表面展开图折叠成正方体后,相对面上的两个数之和为5,求x+y+z的值.
( http: / / www.21cnjy.com )
【解析】正方体的表面展开图,共有六 ( http: / / www.21cnjy.com )个面,其中面“z”与面“3”相对,面“y”与面“-2”相对,面“x”与面“10”相对.则z+3=5,y+(-2)=5,x+10=5,解得z=2,y=7,x=-5.故x+y+z=4.
多边形及其分割
1.从多边形的一个顶点出发,分别连结这个点与其余各个顶点,得到十个三角形,那么这个多边形的边数为 ( )
A.8 B.10 C.12 D.14
【解析】选C.从一个n边形的某个顶点出发,可以引(n-3)条对角线,把n边形分为(n-2)个三角形.
由题意可知,n-2=10,
解得n=12.所以这个多边形的边数为12.
2.把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是 ( )
A.六边形 B.五边形
C.四边形 D.三角形
【解析】选A.当剪去一个角后,剩下的部分是一个四边形,则这张纸片原来的形状可能是四边形或三角形或五边形,不可能是六边形.
【特别提醒】对于本题学生易错误地认为,剪去一个角所得的多边形一定比原多边形少一条边.
3.(2014·大连实验质检)下列图形中,六边形有 (在横线上写上图形的序号).
( http: / / www.21cnjy.com )
【解析】六边形是指由六条线段首尾相接形成的封 ( http: / / www.21cnjy.com )闭多边形,(4)中有曲线,(5)中的线段不是首尾相接而成的封闭图形,不属于多边形,(1)(2)(3)符合六边形的特点,是六边形.
答案:(1)(2)(3)
4.(2014·衢州模拟) ( http: / / www.21cnjy.com )用若干根火柴可以摆出六个正方形,如图就是一种摆法,要摆出六个正方形至多需要 根火柴,至少需要 根火柴(摆出的六个正方形中,每个正方形的边仅限于一根火柴).
【解析】如图:
( http: / / www.21cnjy.com )
所以至多24根,至少17根
答案:24 17
5.下列图形,至少可以分割成多少个三角形
( http: / / www.21cnjy.com )
【解析】图形(1)至少分割成两个三角形.如图所示.
( http: / / www.21cnjy.com )
图形(2)至少分割成三个三角形.如图所示.
( http: / / www.21cnjy.com )
图形(3)至少分割成三个三角形,如图,过每个顶点都可以将它分割成三个三角形.
( http: / / www.21cnjy.com )
图形(4)至少分割成四个三角形,如图所示.
( http: / / www.21cnjy.com )
【错在哪?】作业错例 课堂实拍
画出两种正方体的表面展开图.
( http: / / www.21cnjy.com )
(1)找错:上面解析过程 (填“有”或“无”)错误.
(2)纠错:
答案:(1)有
(2)答案不唯一.
( http: / / www.21cnjy.com )
复习题训练及解析(四)
直线、射线、线段的表示方法
1.如图所示的各直线的表示中,正确的是 ( )
( http: / / www.21cnjy.com )
【解析】选B.直线有两种表示方法:①一个小写字母;②两个大写字母.
2.如图所示,能用图中的字母表示出来的线段、射线的条数分别为 ( )
A.3条,3条 B.6条,3条
C.6条,6条 D.6条,4条
【解析】选B.线段AB,AC,AD,BC,BD,CD共6条,射线AB,BC,CD共3条.
【归纳整合】在一条直线上取n个点得到的线段的条数
每两个点就有一条线段,每取一个点为“线段其中一个端点”,就有(n-1)个“另一个端点”.所以,就有n(n-1)条线段.不过这里面,线段两个端点均重复,每条线段等于计算了两次,需要减半,共有n(n-1)条线段.
3.(2014·河南模拟)下列说法中正确的语句共有 ( )
①直线AB与直线BA是同 ( http: / / www.21cnjy.com )一条直线;②线段AB与线段BA表示同一条线段;③射线AB与射线BA表示同一条射线;④延长射线AB至C,使AC=BC;⑤延长线段AB至C,使BC=AB;⑥直线总比线段长.
A.2个 B.3个 C.4个 D.5个
【解析】选B.直线AB与直线BA是同一 ( http: / / www.21cnjy.com )条直线,字母无顺序要求;线段AB与线段BA表示同一条线段,字母无顺序要求;射线AB与射线BA表示两条不同的射线,端点不同,方向不同;不能延长射线;直线不能度量,所以不能与线段作比较.
【知识归纳】线段、射线、直线的区别与联系
是否可延长 是否可度量 端点个数
线段 是 是 2
射线 是 否 1
直线 否 否 0
注:线段与射线都是直线的一部分
4.如图,能够相交的是 ( )
( http: / / www.21cnjy.com )
【解析】选B.两条直线无限延长后相交.
5.图中的直线是 ,射线有 条,线段有 条.
【解析】直线只有一条是直线BC;以B和C为端点的射线分别有两条,故共有4条射线;线段有3条:线段AB,线段BC,线段AC.
答案:直线BC 4 3
【加固训练】如图中直线的条数为 ( )
( http: / / www.21cnjy.com )
A.1条 B.2条 C.4条 D.6条
【解析】选A.只有1条直线AC.
6.京石高铁运行途中停靠的车站依次是: ( http: / / www.21cnjy.com )北京西站、新涿州、新高碑店、新保定、新定州、正定国际机场、石家庄新客站,那么要为这列火车制作的火车票有
种.
【解析】画一条直线,在直线上依次取 ( http: / / www.21cnjy.com )A,B,C,D,E,F,G七个点,它们依次表示北京西站、新涿州、新高碑店、新保定、新定州、正定国际机场、石家庄新客站.点A分别与B,C,D,E,F,G形成6条线段;点B分别与C,D,E,F,G形成5条线段;点C分别与D,E,F,G形成4条线段;点D分别与E,F,G形成3条线段;点E分别与F,G形成2条线段;点F与G形成1条线段,所以直线上共有线段的条数是6+5+4+3+2+1=21.
因为车票的起点与终点不同,所以应有21×2=42种车票.
答案:42
【知识拓展】若一条直线有n个点,那么以这n个点中的任意两点为端点的线段共有(n-1)+(n-2)+…+2+1=n(n-1)(条).
7.如图所示,点D,E是线段AC上两点,
(1)图中有几条线段,它们分别是哪几条
(2)有几条直线,分别是哪几条 有几条射线,分别是哪几条
【解析】根据线段、射线、直线的概念,通过观察图形可以得到以下结论:
(1)图中共有8条线段,它们分别是线段AB、线段AD、线段AE、线段AC、线段DE、线段DC、线段EC和线段BC.
(2)图中共有1条直线,是直线AB;图中共有6条射线,它们分别是射线BM、射线AB、射线BA、射线AG、射线BC和射线CH.
线段和直线性质的应用
1.下列四个生活、生产现象:
①用两个钉子就可以把木条固定在墙上;②植 ( http: / / www.21cnjy.com )树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用基本事实“两点之间,线段最短”来解释的现象有 ( )
A.①② B.①③ C.②④ D.③④
【解析】选D.①②现象可以用两点可以确定一条直线来解释;③④现象可以用两点之间,线段最短来解释.
2.建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,这种做法用几何知识解释应是 ( )
A.两点之间,线段最短
B.两点之间,直线最短
C.两点确定一条直线
D.三个点不能在同一直线上
【解析】选C.此做法的目的是让墙建得更直,应用的原理为:两点确定一条直线.
【变式训练】如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是 ( )
A.线段有两个端点
B.两条直线相交,只有一个交点
C.两点之间,线段最短
D.两点确定一条直线
【解析】选D.经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是两点确定一条直线.
3.在看中央电视台“动物世界”节目时 ( http: / / www.21cnjy.com ),我们可以看到这样的画面,非洲雄狮在广阔的草原上捕食鹿时,总是沿直线狂奔,其中蕴含的数学知识是 .
【解析】沿直线狂奔所蕴含的数学知识是两点之间,线段最短.
答案:两点之间,线段最短
4.如图,已知A,B,C,D四点.
(1)经过这四点最多能确定 条线段.
(2)如果这四点是公园里湖面上桥的支撑 ( http: / / www.21cnjy.com )点,图中黑的实线表示桥面,从B地到C地有两座桥如图所示,若想在B,C之间铺设自来水管道,从节省材料的角度考虑,应选择图中①,②两条路中的哪一条,为什么 如果有人想在桥上较长时间观赏湖面风光,应选择哪条路线 说说你的理由.
【解析】(1)根据过n个点最多可确定条直线,
可得当n=4时,==6(条).
(2)根据两点之间线段最短可知②的长度短,①的长度长.所以从节省材料的角度考虑,应选择②,如果有人想在桥上较长时间观赏湖面风光,应选择①.
【错在哪?】作业错例 课堂实拍
如图,射线OA与射线OB表示的是同一条射线吗 射线AB与射线BA是同一条射线吗
( http: / / www.21cnjy.com )
(1)找错:上面解析过程 (填“有”或“无”)错误.
(2)纠错: .
答案:(1)有
(2)虽然表示射线OA,OB的字母不同,但它们的端点相同,方向一致,是同一条射线;射线AB,BA的端点不同,不是同一条射线.
复习题训练及解析(五)
线段的长短比较
1.比较线段a和b的长短,其结果一定是 ( )
A.a=b B.a>b
C.ab或a=b或a【解析】选D.比较线段a和b的长短,其结果有三种情况:a>b或a=b或a【方法技巧】线段长短比较的两种方法
1.度量法:用刻度尺量出两条线段的长度,再比较长短.
2.叠合法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.
2.根据图形,比较两条线段长度的大小.
(1)线段OA与OB.
答: .
(2)线段AB与AD.
答: .
【解析】(1)由叠合法得OB>OA.
(2)由度量法或圆规截取法得AD>AB.
答案:(1)OB>OA (2)AD>AB
3.如图所示,利用圆规比较图中线段的长短,并用“>”“=”“<”填空.
( http: / / www.21cnjy.com )
(1)AB AC.
(2)AD AC.
(3)AF AC.
(4)AE BC.
(5)BC AB.
【解析】利用圆规比较AB与AC ( http: / / www.21cnjy.com )时,圆规的一支点与A重合,另一支点与C重合,则两张角之间的长度就是AC的长度,保持这个张角,把圆规放在线段AB上,使一支点与A重合,另一支点落在线段AB之间,故AB>AC.用同样的方法可以比较其他几对线段.
答案:(1)> (2)= (3)< (4)< (5)=
4.如图所示,线段a,b,且a>b.
( http: / / www.21cnjy.com )
用圆规和直尺画线段:(1)a+b.(2)a-b.
【解析】(1)画法如图(1),画直线A ( http: / / www.21cnjy.com )F,在直线AF上画线段AB=a,再在AB的延长线上画线段BC=b,线段AC就是a与b的和,记作AC=a+b.
(2)画法如图(2),画直线AF,在直线AF上画线段AB=a,再在线段AB上画线段BD=b,线段AD就是a与b的差,记作AD=a-b.
( http: / / www.21cnjy.com )
5.已知线段a,b,求作线段AB=3a-b.
( http: / / www.21cnjy.com )
【解析】如图:(1)画射线AM.
(2)在射线AM上截取AC,使AC=3a.
(3)在线段AC上截取BC,使BC=b;则线段AB即为所求.
线段的有关计算
1.(2014·山师附中质检)如果线段AB=13cm,MA+MB=17cm,那么下面说法中正确的是 ( )
A.点M在线段AB上
B.点M在直线AB上
C.点M在直线AB外
D.点M可能在直线AB上,也可能在直线AB外
【解析】选D.因为线段AB=13cm,MA+MB=17cm,所以点M可能在线段AB或BA的延长线上,也可能在直线AB外.
2.如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是 ( )
A.CD=AC-BD B.CD=BC
C.CD=AB-BD D.CD=AD-BC
【解析】选B.因为C是线段AB的中点,所以AC=BC,所以CD=BC-BD=AC-BD=AB-BD=AD-AC=AD-BC.
3.判断下列语句中:
①线段AB就是A,B两点间的距离;
②线段AB的一半就是线段AB的中点;
③在所有连结两点的线中直线最短;
④如果AB=BC=CD,则AD=3AB.
其中错误语句的个数是 ( )
A. 0 B. 2 C. 3 D. 4
【解析】选D.线段AB和线段AB的中点都是 ( http: / / www.21cnjy.com )几何图形,而A,B两点间的距离和线段AB的一半都是数量,形与数不能划等号;③把线段与直线的性质混淆了;④中的三条线段可能不在一条直线上,因此,这四个语句都是错误的.
4.线段AD=6cm,线段AC=BD=4cm,E,F分别是线段AB,CD的中点,求线段EF的长.
【解析】因为线段AD=6cm,线段AC=BD=4cm,
所以BC=AC+BD-AD=4+4-6=2cm.
所以AB+CD=AD-BC=6-2=4cm.
又因为E,F分别是线段AB,CD的中点,
所以EB=AB,CF=CD,
所以EB+CF=AB+CD=(AB+CD)=2cm,
所以EF=EB+BC+CF=2+2=4(cm).
【知识归纳】线段的计算
1.线段的长度和有理数一样,可以进行加减等运算.
2.如果题目中没有图形,一定要先画出图形,数形结合思想是数学学习的一种重要方法,应特别注意对线段的中点的灵活运用.
5.如图所示,点C,D为线段AB的三等分点(即分成相等的三等份),点E为线段AC的中点,若ED=9,求线段AB的长度.
【解析】因为C,D为线段AB的三等分点,
所以AC=CD=DB.
又因为点E为AC的中点,则AE=EC=AC,
所以CD+EC=DB+AE.
因为ED=EC+CD=9,
所以DB+AE=EC+CD=ED=9,
则AB=2ED=18.
【错在哪?】作业错例 课堂实拍
已知线段AB=12cm,AB所在的直线上有一点C,且BC=6cm,D是线段AC的中点,求线段AD的长.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错: .
答案:(1)①
(2)本题漏掉了第二种情况:当点C在线段AB的延长线上时,此时AD=
(AB+BC)=(12+6)=9 cm.
复习题训练及解析(六)
角的识别与表示
1.下图中表示∠ABC的是 ( )
( http: / / www.21cnjy.com )
【解析】选C.选项B不是角,用三个大写字母表示角时,中间的字母表示角的顶点.
2.下列关于角的说法中,正确的个数为 ( )
①两条射线所组成的图形叫做角;②角是一条射线从一个位置旋转到另一个位置所组成的图形;③两条射线,它们的端点重合时,可以形成角.
A. 0 B. 1 C. 2 D.3
【解析】选B.①中忽视组成角的两条射线必须有公共点;②中没有确定是否绕着它的端点旋转到另一个位置;③是正确的.
3.(2014·赤峰实验质检)如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是 ( )
( http: / / www.21cnjy.com )
【解析】选D.∠O是一个单独的大写英文字母,它只能表示独立的一个角,而∠O还可用∠1或∠AOB表示.
4.如图,以O为顶点且小于180°的角一共有多少个
( http: / / www.21cnjy.com )
【解题指南】解答本题的基本思路:
1.先数出以OM为一边的角.
2.再数出以OA,OB…为一边的角.
3.然后把它们加起来.
【解析】7+6+5+4+3+2+1==28.
【方法技巧】确定角的个数
1.数角的个数时必须做到不重不漏.
2.同一个平面内,从一个顶点出发有n条射线时,形成角的个数与一条直线上n个点形成线段的个数类似,为.
5.如图,请指出OA是表示什么方向的一条射线 依照这条射线画出表示下列方向的射线:
( http: / / www.21cnjy.com )
(1)南偏东20°.(2)北偏西50°.(3)东南方向(即南偏东45°).
【解析】OA方向可表示为南偏东65°.(1)(2)(3)如图所示,OB表示南偏东
20°,OC表示北偏西50°,OD表示东南方向.
( http: / / www.21cnjy.com )
角的度、分、秒的换算
1.36.33°可化为 ( )
A.36°30′3″ B.36°33′
C.36°30′30″ D.36°19′48″
【解析】选D.因为0.33×60′=19.8′,0.8×60″=48″,
所以36.33°=36°19′48″.
【易错提醒】要注意进位原则(满60进1)和退位原则(借1当60).
2.在时刻为8:30时,钟表上的时针和分针之间的夹角为 °.
【解析】钟表一周可视为360°,被分成12个大格,每格对应30°.8:30时,时针与分针夹角恰为2.5个格.
故30°×2.5=75°.
答案:75
3.(1)48′= °.(2)39°36′= °.
【解析】(1)48′=48×°=0.8°.
(2)因为36′=36×°=0.6°,所以39°36′=39.6°.
答案:(1)0.8 (2)39.6
4.(2014·新沂实验质检)将26°48′36″用度表示.
【解析】把36″化成分,36″=′×36=0.6′,
48′+0.6′=48.6′,
把48.6′化成度,48.6′=°×48.6=0.81°.
所以26°48′36″=26.81°.
【知识归纳】角的度、分、秒的换算
1.用度、分、秒表示度时,要先把度的小数部分化成分,再把分的小数部分化成秒,用公式1°=60′,1′=60″.
2.用度表示度、分、秒时,要先把秒化成分,再把分化成度,用公式1″=′,
1′=°.
5.(1)把26.29°转化为度、分、秒表示的形式.
(2)把33°24′36″转化成度表示的形式.
【解析】(1)26.29°=26°+0.29°=26°+0.29×60′=26°+17.4′
=26°+17′+0.4×60″=26°17′+24″=26°17′24″.
(2)33°24′36″=33°+24′+36×′=33°+24′+0.6′=33°+24.6′=33°+24.6×°=33.41°.
【变式训练】
(1)1.05°等于多少分 等于多少秒
(2)将70.23°用度、分、秒表示.
【解析】(1)60′×1.05=63′;3600″×1.05=3780″.
所以1.05°等于63′,等于3780″.
(2)将0.23°化为分,可得0.23×60′=13.8′,
再把0.8′化为秒,得0.8×60″=48″.
所以70.23°=70°13′48″.
【错在哪?】作业错例 课堂实拍
写出图中所有小于平角的角.
( http: / / www.21cnjy.com )
(1)错因:
(2)纠错:
答案:(1)以C为顶点的小于平角的角有两个,错解中遗漏一个,且以点C为顶点的角不止一个,不能用顶点处的大写字母表示角.
(2)图中小于平角的角有:∠A,∠B,∠ACB,∠ACD.
复习题训练及解析(七)
角的比较
1.在∠AOB的内部任取一点C,作射线OC,那么有 ( )
A.∠AOC=∠BOC B.∠AOC>∠BOC
C.∠AOC>∠AOB D.∠AOB>∠AOC
【解析】选D.射线OC在∠AOB的内部,那么∠AOC在∠AOB的内部,且有一公共边OA,所以存在∠AOB>∠AOC.
2.如图所示,如果∠AOD>∠BOC,那么下列说法正确的是 ( )
A.∠COD>∠AOB
B.∠AOB>∠COD
C.∠COD=∠AOB
D.∠AOB与∠COD的大小关系不能确定
【解析】选B.因为∠AOD与 ( http: / / www.21cnjy.com )∠BOC中都包含∠BOD,所以都减去它,不等式仍成立,因为∠AOD>∠BOC,所以∠AOD-∠BOD>∠BOC-∠BOD,即∠AOB>∠COD.
3.如图,∠AOB,∠COD都是直角,那么∠DOB与∠AOC的大小关系是∠DOB ∠AOC.
【解析】由题意∠AOB,∠COD都是直角,
所以∠AOD+∠DOB=∠AOC+∠AOD=90°,
所以∠DOB=∠AOC.
答案:=
4.根据图,比较∠AOC,∠BOD,∠BOC,∠COD,∠AOD的大小,它们从小到大排列为 .
【解析】由图可观察出:∠BOC<∠COD;
∠COD<∠BOD;
∠AOD最大;
∠AOC=∠BOD=90°.
答案:∠BOC<∠COD<∠AOC=∠BOD<∠AOD
5.比较大小:直角 锐角;38.51° 38°50′1″.
【解析】直角=90°,锐角大于0°而小于90°.
故直角>锐角;38.51°=38°30′36″<38°50′1″.
答案:> <
角的平分线及相关计算
1.如图,∠AOD-∠AOC= ( )
A.∠ADC B.∠BOC
C.∠BOD D.∠COD
【解析】选D.结合图形,显然∠AOD-∠AOC=∠COD.
2.(2014·襄阳模拟)如图,∠BOC=40°,OD平分∠AOC,∠AOD=25°,那么∠AOB等于 ( )
( http: / / www.21cnjy.com )
A.65° B.50° C.40° D.90°
【解析】选D.因为OD平分∠AOC,∠AOD=25°,
所以∠AOC=2∠AOD=50°,
所以∠AOB=∠AOC+∠BOC=90°.
3.(2013·广州中考)已知∠ABC=30°,BD是∠ABC的平分线,则
∠ABD= .
【解析】∠ABD=∠ABC=×30°=15°.
答案:15°
4.如图,OB是 的角平分线;OC是 的角平分线,
∠AOD= ,∠BOD= .
( http: / / www.21cnjy.com )
【解析】由题意知,OB是∠AOC的角平分线;OC是∠AOD的角平分线,因为
∠COD=30°,所以∠AOD=60°,∠BOD=∠BOC+∠COD=45°.
答案:∠AOC ∠AOD 60° 45°
5.如图,已知∠AOC=∠BOD=75°,∠BOC=30°,则∠AOD= .
( http: / / www.21cnjy.com )
【解析】因为∠AOC=75°,∠BOC=30°,
所以∠AOB=∠AOC-∠BOC=75°-30°=45°,
又因为∠BOD=75°,
所以∠AOD=∠AOB+∠BOD=45°+75°=120°.
答案:120°
6.计算:(1)12°17′×4.
(2)159°52′÷5(精确到分).
【解析】(1)12°17′×4=12°×4+17′×4
=48°+68′=48°+(1°+8′)=49°8′.
(2)159°52′÷5
=159°÷5+52′÷5=31°+4°52′÷5
=31°+(4×60′+52′)÷5
≈31°58′.
【知识归纳】角度的运算
1.角度相加,应是度与度相加,分与分相加,秒与秒相加.但要注意度、分、秒之间的进位是60进制,进位时,60″=1′,60′=1°.
2.角度相减,度与度相减,分与分相减, ( http: / / www.21cnjy.com )秒与秒相减.当分与分相减不够减时,应向度借,当秒与秒相减不够减时,应向分借,借位时,1°=60′,1′=60″.
3.角度与数字相乘,就是用度、分、秒分别与数字相乘,如果满60分要进1度,60秒要进1分.
4.角度除以数字,先用度除以数字,如果 ( http: / / www.21cnjy.com )度有余数,要将度余数乘以60化为分,然后再用分除以数字,若有余数,再把余数乘以60化成秒,再用秒除以数字.并注意题中要求的精确度,进行四舍五入.
7.(2014·巴中实验质检)如图,(1)∠AOC是哪两个角的和.
(2)∠AOB是哪两个角的差.
(3)如果∠AOB=∠COD,那么∠AOC与∠DOB相等吗
( http: / / www.21cnjy.com )
【解析】(1)∠AOC是∠AOB与∠BOC的和.
(2)∠AOB是∠AOC与∠BOC的差,或∠AOB是∠AOD与∠BOD的差.
(3)因为∠AOB=∠COD,
所以∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠DOB.
【知识归纳】对角的和差关系的理解
1.从“形”的方面理解:画一个角等于已知两角的和(或差).
2.从“数”的方面理解:一个角的度数等于已知两个角的度数的和(或差).
【错在哪?】作业错例 课堂实拍
平面内有两个角,∠AOB=50°,∠AOC=20°,OA为两角的公共边,则∠BOC
为 ( )
A.30° B.70°
C.30°或70° D.无法确定
( http: / / www.21cnjy.com )
(1)错因:
(2)纠错:
答案:(1)本题误认为OB,OC在OA的同侧,遗漏OB,OC在OA两侧的情况.
(2)选C.①如图,当OC落在∠AOB的内部时,∠BOC=∠AOB-∠AOC=50°-20°
=30°.
( http: / / www.21cnjy.com )
②如图,当OC落在∠AOB的外部时,
∠BOC=∠AOB+∠AOC=50°+20°=70°.
综上所述,∠BOC为30°或70°.
复习题训练及解析(八)
余角和补角
1.下列说法正确的个数为 ( )
①锐角的补角一定是钝角;
②一个角的补角一定大于这个角;
③如果两个角是同一个角的补角,那么它们相等;
④锐角和钝角互补.
A.1个 B.2个 C.3个 D.4个
【解析】选B.设一个角为∠α,则与它互补 ( http: / / www.21cnjy.com )的角为∠β=180°-∠α.①当∠α为锐角时,∠α<90°,所以∠β>90°,所以∠β为钝角,①正确;②同理,若∠α为钝角,则它的补角∠β为锐角,∠β<∠α,②不正确;③设∠α+∠β=180°,
∠γ+∠β=180°,所以∠α=∠γ,③正确;④中没有明确指出角的值,因此④不正确.故只有①③成立,故选B.
【知识归纳】互余、互补角的特点
1.互余的两个角必须都是锐角.
2.互补的两个角可以一个是锐角另一个是钝角,也可以两个角都是直角.
2.下列图形中,∠1和∠2互为余角的是 ( )
( http: / / www.21cnjy.com )
【解析】选D.由题意知,选项A中∠1与∠2既不互补也不互余,选项B中∠1和∠2互补,选项C中∠1和∠2相等,选项D中∠1和∠2互余.
【变式训练】(2012·长沙中考)下列四个角中,最有可能与70°角互补的
是 ( )
( http: / / www.21cnjy.com )
【解析】选D.70°角的补角=180°-70 ( http: / / www.21cnjy.com )°=110°,是钝角,结合各选项,只有D选项是钝角,所以,最有可能与70°角互补的是D选项的角.
3.(2014·郴州实验质检)一个角的余角比它的补角的少20°,则这个角为
( )
A.30° B.40° C.60° D.75°
【解析】选B.设这个角为x°,则它的余角为(90-x)°,
它的补角为(180-x)°,
根据题意,得90-x=(180-x)-20,
解方程,得x=40.
4.(2013·泰州中考)已知∠α的补角是130°,则∠α= .
【解析】根据互为补角的定义,∠α=180°-130°=50°.
答案:50°
【变式训练】48°16′的补角是 ,
72°39′16″的余角是 .
【解析】48°16′的补角为180°-48°16′=131°44′,
72°39′16″的余角为90°-72°39′16″=17°20′44″.
答案:131°44′ 17°20′44″
5.已知:如图所示,AB是直线,∠BOC=∠AOC=90°,OD,OE是射线,则图中有 对互余的角, 对互补的角.
( http: / / www.21cnjy.com )
【解析】∠AOE与∠EOC,∠BOD与∠COD互余;∠AOE与∠BOE,∠BOD
与∠AOD,∠AOC与∠BOC互补.
答案:2 3
6.如图,O是直线AB上的点,OC是∠AOB的平分线,
( http: / / www.21cnjy.com )
(1)∠AOD的补角是 ,余角是 .
(2)∠DOB的补角是 .
【解析】因为OC是∠AOB的平分线, ( http: / / www.21cnjy.com )所以∠AOC=∠BOC=90°,所以∠AOD的补角是∠BOD,余角是∠COD,∠DOB的补角是∠AOD.
答案:(1)∠BOD ∠COD (2)∠AOD
7.如图,∠AOB是直角,∠COD=90°,OB平分∠DOE,则∠3与∠4是什么关系 并说明理由.
( http: / / www.21cnjy.com )
【解析】∠3=∠4,理由如下:
因为∠AOB是直角,∠COD=90°,
所以∠1+∠2=90°,∠1+∠3=90°,
所以∠2=∠3,
因为OB平分∠DOE,
所以∠2=∠4,所以∠3=∠4.
8.一个角的余角和它的补角之比是3∶7,求这个角的度数.
【解析】设余角为3x°,补角为7x°,
由题意得7x-3x=90,4x=90,x=22.5.
所以这个角为90°-3x°=90°-67.5°=22.5°.
答:这个角的度数为22.5°.
【错在哪?】作业错例 课堂实拍
如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
( http: / / www.21cnjy.com )
(1)指出图中∠AOD与∠BOE的补角.
(2)试说明∠COD与∠COE具有怎样的数量关系.
( http: / / www.21cnjy.com )
(1)错因:
(2)纠错:
答案:(1) (1)中找的补角不全.(2)∠COD与∠COE互余.
(2) (1)∠AOD的补角是∠BOD,∠COD,∠BOE的补角是∠AOE,∠COE.(2)∠COD
与∠COE互余.理由:因为OD平分∠BOC,OE平分∠AOC,所以∠COD=∠BOC,
∠COE=∠AOC,又∠BOC+∠AOC=180°,所以∠COD+∠COE=90°.
常见的几何体
1.在六角螺母、哈密瓜、易拉罐、足球、字典中,物体的形状类似于棱柱的个数是 ( )
A.0 B.1 C.2 D.3
【解析】选C.六角螺母、字典都有上、下两个底面,并且底面都是多边形,因此它们都类似于棱柱.故选C.
2.(2014·乐山实验月考)下面几何图形中,是棱柱的是 ( )
( http: / / www.21cnjy.com )
【解题指南】判断棱柱的两个关键点
(1)由上下两个底面以及侧面组成.
(2)上下两个底面是完全相同的多边形,侧面是四边形.
【解析】选B.棱柱的侧面应是四边形,符合这个条件的只有选项B中的几何体.
【知识拓展】棱柱的性质
区别名称 顶点数 底面数 侧面数 总面数 侧棱数 总棱数
三棱柱 6 2 3 5 3 9
四棱柱 8 2 4 6 4 12
五棱柱 10 2 5 7 5 15
六棱柱 12 2 6 8 6 18
… … … … … … …
n棱柱 2n 2 n n+2 n 3n
3.(2014·山师附中质检)在下列四个立体图形中,不是多面体的是 ( )
( http: / / www.21cnjy.com )
【解析】选D.A项中立体图形由四个平的面围成,B,C项中立体图形均由6个平的面围成,D项中立体图形有2个面,一个曲面,一个平面.
4.生活中有许多立体图形,如一个皮球可以看作 体,一枝铅笔可以看作
体,一节火车车厢可以看作 体.
【解析】解决此类问题,要熟悉生活中的立体图形,清楚立体图形的特征.皮球可以看作球体,铅笔可以看作柱体,一节火车车厢可以看作长方体.
答案:球 柱 长方
5.判断如图所示的图形中球体有 ;多面体有 .
( http: / / www.21cnjy.com )
【解析】只有一个曲面的有②③④,所以球体是②③④;由四个或四个以上多边形所围成的立体图形为①⑤⑦,所以多面体是①⑤⑦.
答案:②③④ ①⑤⑦
【易错提醒】判断一个几何体是否是多面体时,不能看到一个几何体有多个面就判断为多面体,要注意多面体的每个面都是平面.
6.如图,实物图是一些具体的图形——三棱 ( http: / / www.21cnjy.com )镜、方砖、帆布帐篷、笔筒、铅锤、粮囤、东方明珠,下图中是一些立体图形,找出与立体图形类似的实物图形.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
【解析】要准确判断出实物的几何体的形状,平时要多注意观察,也可用类似的实物作为参照.
答案:(a)3 (b)7 (c)4 (d)5 (e)2 (f)1 (g)6
【知识归纳】圆锥与棱锥的联系与区别
(1)相同点:都有一个底面,一个顶点.
(2)不同点:圆锥的底面是圆形,棱锥的底面是多边形;圆锥的侧面是一个曲面,棱锥的侧面是由几个平面围成的,且每个平面都是三角形.
7.请你把相应的实物与图形用线连结起来.
( http: / / www.21cnjy.com )
答案:
( http: / / www.21cnjy.com )
【错在哪?】作业错例 课堂实拍
填空:判断下列实物类似于哪一种几何体.
(1)数学课本是 .
(2)粉笔是 .
( http: / / www.21cnjy.com )
(1)找错:上面解析过程 (填“有”或“无”)错误.
(2)纠错: .
答案: (1)有 (2)数学课本的形状是长方体,粉笔的侧面是曲面,两个底面是两个大小不相等的圆,是圆台.
答案:(1)长方体 (2)圆台
复习题训练及解析(二)
由立体图形到三视图
1.(2013·盐城中考)下面的几何体中,主视图不是长方形的是 ( )
( http: / / www.21cnjy.com )
【解析】选C.选项A,B,D图形的主视图是矩形,只有选项C图形的主视图是等腰梯形.
2.(2013·湛江中考)如图是由6个大小相同的正方体组成的几何体,它的左视图是 ( )
( http: / / www.21cnjy.com )
【解析】选A.从左边看,左边一列有两个正方形,右边有一个.
3.(2013·衡阳中考)下列几何体,同一个几何体的主视图与俯视图不同的是
( )
( http: / / www.21cnjy.com )
【解析】选C.图中圆柱的主视图和俯视图都是 ( http: / / www.21cnjy.com )长方形;正方体的正视图和俯视图都是正方形;球的正视图和俯视图都是圆;圆锥的正视图是三角形,俯视图是圆,故选C.
【知识拓展】常见几何体的三视图
几何体视图
主视图
左视图
俯视图
4.(2013·广州中考)如图所示的几何体的主视图是 ( )
( http: / / www.21cnjy.com )
【解析】选A.因为选项B是两个矩形,中间有分隔线,显然不是主视图,而选项C是这个图形的俯视图,选项D不是三视图,
所以确定主视图为选项A.
5.(2013·潍坊中考)如图是常用的一种圆顶螺杆,它的俯视图正确的是 ( )
( http: / / www.21cnjy.com )
【解析】选B.因为圆柱俯视图是一个圆,大圆与小圆组合在一起,所以这个组合体的俯视图是B选项中的图形.
6.已知由四个大小相同的小正方体搭成的几何体如图所示,请画出该几何体的三视图.
( http: / / www.21cnjy.com )
【解析】从正面看有2列,左列有2个正方形,右列有1个正方形;
从左面看有2列,左列有2个正方形,右列有1个正方形;
从上面看也有2列,左列有1个正方形,右列有2个正方形.如图所示:
( http: / / www.21cnjy.com )
由三视图到立体图形
1.某几何体的三视图如图所示,则这个几何体是 ( )
( http: / / www.21cnjy.com )
A.圆柱 B.正方体
C.球 D.圆锥
【解析】选D.根据主视图和左视图为三角形判断出是锥体,根据俯视图是圆形及圆心可判断出这个几何体是圆锥.
【知识归纳】几何体与三视图的联系
已知一个立体图形,可以画出它的三视图,由三 ( http: / / www.21cnjy.com )视图也可以画出几何体.先根据主视图和左视图可以确定几何体是柱体还是锥体,再依据俯视图确定是棱体还是圆体;两方面结合可以确定这个几何体.
2.(2013·内江中考)一个几何体的三视图如图所示,那么这个几何体是 ( )
( http: / / www.21cnjy.com )
【解析】选C.从俯视图看, ( http: / / www.21cnjy.com )它是一个三角形,而选项A和B的俯视图是圆,不可能出现三角形,所以排除A,B,从左视图看,它是一个长方形,而选项D的左视图是三角形,不可能出现长方形,所以排除D,只有选项C符合题意.
3.图中三视图所对应的几何体是 ( )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
【解析】选C.从主视图可以排除选项A,B,从俯视图排除选项D,故选C.
4.一个立体图形的三视图是三个圆,则这个图形是 .
【解析】球体的三视图都是圆,这个图形是球体.
答案:球体
【错在哪?】作业错例 课堂实拍
画出下列几何体的三视图.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)找错:上面解析过程 (填“有”或“无”)错误.
(2)纠错:
答案:(1)有
(2)
( http: / / www.21cnjy.com )
复习题训练及解析(三)
立体图形与平面图形的转化
1.(2013·恩施中考)如图,下列四个选项中,不是正方体表面展开图的是
( )
( http: / / www.21cnjy.com )
【解析】选C.选项A,B,D都可以折叠成一个正方体,只有选项C不能折叠成正方体,因此,选项C不是正方体的表面展开图,所以,本题应选C.
【知识拓展】正方体表面展开图(一四一型6种)口诀:中间四个一连串,两边各一随便放.
( http: / / www.21cnjy.com )
(二三一或一三二型3种)口诀:二三紧连挪一个,三一相连一随便.
( http: / / www.21cnjy.com )
(二二二型1种)口诀:两两相连各挪一.
( http: / / www.21cnjy.com )
(三三型1种)口诀:三个两排一对齐.
( http: / / www.21cnjy.com )
2.(2013·河南中考)如图是正方体的一种展开图,其每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是 ( )
A.1 B.4 C.5 D.6
【解析】选B.由展开图可知正方体的相对面分别为:1与6相对,2与4相对,3与5相对.
3.如图所示的平面图形中,不可能围成圆锥的是 ( )
( http: / / www.21cnjy.com )
【解析】选D.展开想象,把平面图形折叠成体,检查折叠成的立体图形是否为圆锥.
【归纳整合】圆柱、圆锥的表面展开图
圆柱的表面展开图是由两个相同的圆形和一个矩形组成的,圆锥的表面展开图是由一个圆形和一个扇形组成的.
4.(2013·南京中考)如图,一个几 ( http: / / www.21cnjy.com )何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色.下列图形中,是该几何体的表面展开图的是 ( )
( http: / / www.21cnjy.com )
【解题指南】观察带颜色的小正方形所在的位置排除A,C选项,再根据正方体表面展开图的特点排除D.
【解析】选B.通过观察涂黑正方形一 ( http: / / www.21cnjy.com )面接着一个三角形,三面接着三个正方形,A,C答案均不直接和三角形相接,D选项不能围成密封的几何体,所以不选,只有B选项符合.
5.若要使得图中的表面展开图折叠成正方体后,相对面上的两个数之和为5,求x+y+z的值.
( http: / / www.21cnjy.com )
【解析】正方体的表面展开图,共有六 ( http: / / www.21cnjy.com )个面,其中面“z”与面“3”相对,面“y”与面“-2”相对,面“x”与面“10”相对.则z+3=5,y+(-2)=5,x+10=5,解得z=2,y=7,x=-5.故x+y+z=4.
多边形及其分割
1.从多边形的一个顶点出发,分别连结这个点与其余各个顶点,得到十个三角形,那么这个多边形的边数为 ( )
A.8 B.10 C.12 D.14
【解析】选C.从一个n边形的某个顶点出发,可以引(n-3)条对角线,把n边形分为(n-2)个三角形.
由题意可知,n-2=10,
解得n=12.所以这个多边形的边数为12.
2.把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是 ( )
A.六边形 B.五边形
C.四边形 D.三角形
【解析】选A.当剪去一个角后,剩下的部分是一个四边形,则这张纸片原来的形状可能是四边形或三角形或五边形,不可能是六边形.
【特别提醒】对于本题学生易错误地认为,剪去一个角所得的多边形一定比原多边形少一条边.
3.(2014·大连实验质检)下列图形中,六边形有 (在横线上写上图形的序号).
( http: / / www.21cnjy.com )
【解析】六边形是指由六条线段首尾相接形成的封 ( http: / / www.21cnjy.com )闭多边形,(4)中有曲线,(5)中的线段不是首尾相接而成的封闭图形,不属于多边形,(1)(2)(3)符合六边形的特点,是六边形.
答案:(1)(2)(3)
4.(2014·衢州模拟) ( http: / / www.21cnjy.com )用若干根火柴可以摆出六个正方形,如图就是一种摆法,要摆出六个正方形至多需要 根火柴,至少需要 根火柴(摆出的六个正方形中,每个正方形的边仅限于一根火柴).
【解析】如图:
( http: / / www.21cnjy.com )
所以至多24根,至少17根
答案:24 17
5.下列图形,至少可以分割成多少个三角形
( http: / / www.21cnjy.com )
【解析】图形(1)至少分割成两个三角形.如图所示.
( http: / / www.21cnjy.com )
图形(2)至少分割成三个三角形.如图所示.
( http: / / www.21cnjy.com )
图形(3)至少分割成三个三角形,如图,过每个顶点都可以将它分割成三个三角形.
( http: / / www.21cnjy.com )
图形(4)至少分割成四个三角形,如图所示.
( http: / / www.21cnjy.com )
【错在哪?】作业错例 课堂实拍
画出两种正方体的表面展开图.
( http: / / www.21cnjy.com )
(1)找错:上面解析过程 (填“有”或“无”)错误.
(2)纠错:
答案:(1)有
(2)答案不唯一.
( http: / / www.21cnjy.com )
复习题训练及解析(四)
直线、射线、线段的表示方法
1.如图所示的各直线的表示中,正确的是 ( )
( http: / / www.21cnjy.com )
【解析】选B.直线有两种表示方法:①一个小写字母;②两个大写字母.
2.如图所示,能用图中的字母表示出来的线段、射线的条数分别为 ( )
A.3条,3条 B.6条,3条
C.6条,6条 D.6条,4条
【解析】选B.线段AB,AC,AD,BC,BD,CD共6条,射线AB,BC,CD共3条.
【归纳整合】在一条直线上取n个点得到的线段的条数
每两个点就有一条线段,每取一个点为“线段其中一个端点”,就有(n-1)个“另一个端点”.所以,就有n(n-1)条线段.不过这里面,线段两个端点均重复,每条线段等于计算了两次,需要减半,共有n(n-1)条线段.
3.(2014·河南模拟)下列说法中正确的语句共有 ( )
①直线AB与直线BA是同 ( http: / / www.21cnjy.com )一条直线;②线段AB与线段BA表示同一条线段;③射线AB与射线BA表示同一条射线;④延长射线AB至C,使AC=BC;⑤延长线段AB至C,使BC=AB;⑥直线总比线段长.
A.2个 B.3个 C.4个 D.5个
【解析】选B.直线AB与直线BA是同一 ( http: / / www.21cnjy.com )条直线,字母无顺序要求;线段AB与线段BA表示同一条线段,字母无顺序要求;射线AB与射线BA表示两条不同的射线,端点不同,方向不同;不能延长射线;直线不能度量,所以不能与线段作比较.
【知识归纳】线段、射线、直线的区别与联系
是否可延长 是否可度量 端点个数
线段 是 是 2
射线 是 否 1
直线 否 否 0
注:线段与射线都是直线的一部分
4.如图,能够相交的是 ( )
( http: / / www.21cnjy.com )
【解析】选B.两条直线无限延长后相交.
5.图中的直线是 ,射线有 条,线段有 条.
【解析】直线只有一条是直线BC;以B和C为端点的射线分别有两条,故共有4条射线;线段有3条:线段AB,线段BC,线段AC.
答案:直线BC 4 3
【加固训练】如图中直线的条数为 ( )
( http: / / www.21cnjy.com )
A.1条 B.2条 C.4条 D.6条
【解析】选A.只有1条直线AC.
6.京石高铁运行途中停靠的车站依次是: ( http: / / www.21cnjy.com )北京西站、新涿州、新高碑店、新保定、新定州、正定国际机场、石家庄新客站,那么要为这列火车制作的火车票有
种.
【解析】画一条直线,在直线上依次取 ( http: / / www.21cnjy.com )A,B,C,D,E,F,G七个点,它们依次表示北京西站、新涿州、新高碑店、新保定、新定州、正定国际机场、石家庄新客站.点A分别与B,C,D,E,F,G形成6条线段;点B分别与C,D,E,F,G形成5条线段;点C分别与D,E,F,G形成4条线段;点D分别与E,F,G形成3条线段;点E分别与F,G形成2条线段;点F与G形成1条线段,所以直线上共有线段的条数是6+5+4+3+2+1=21.
因为车票的起点与终点不同,所以应有21×2=42种车票.
答案:42
【知识拓展】若一条直线有n个点,那么以这n个点中的任意两点为端点的线段共有(n-1)+(n-2)+…+2+1=n(n-1)(条).
7.如图所示,点D,E是线段AC上两点,
(1)图中有几条线段,它们分别是哪几条
(2)有几条直线,分别是哪几条 有几条射线,分别是哪几条
【解析】根据线段、射线、直线的概念,通过观察图形可以得到以下结论:
(1)图中共有8条线段,它们分别是线段AB、线段AD、线段AE、线段AC、线段DE、线段DC、线段EC和线段BC.
(2)图中共有1条直线,是直线AB;图中共有6条射线,它们分别是射线BM、射线AB、射线BA、射线AG、射线BC和射线CH.
线段和直线性质的应用
1.下列四个生活、生产现象:
①用两个钉子就可以把木条固定在墙上;②植 ( http: / / www.21cnjy.com )树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用基本事实“两点之间,线段最短”来解释的现象有 ( )
A.①② B.①③ C.②④ D.③④
【解析】选D.①②现象可以用两点可以确定一条直线来解释;③④现象可以用两点之间,线段最短来解释.
2.建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,这种做法用几何知识解释应是 ( )
A.两点之间,线段最短
B.两点之间,直线最短
C.两点确定一条直线
D.三个点不能在同一直线上
【解析】选C.此做法的目的是让墙建得更直,应用的原理为:两点确定一条直线.
【变式训练】如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是 ( )
A.线段有两个端点
B.两条直线相交,只有一个交点
C.两点之间,线段最短
D.两点确定一条直线
【解析】选D.经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是两点确定一条直线.
3.在看中央电视台“动物世界”节目时 ( http: / / www.21cnjy.com ),我们可以看到这样的画面,非洲雄狮在广阔的草原上捕食鹿时,总是沿直线狂奔,其中蕴含的数学知识是 .
【解析】沿直线狂奔所蕴含的数学知识是两点之间,线段最短.
答案:两点之间,线段最短
4.如图,已知A,B,C,D四点.
(1)经过这四点最多能确定 条线段.
(2)如果这四点是公园里湖面上桥的支撑 ( http: / / www.21cnjy.com )点,图中黑的实线表示桥面,从B地到C地有两座桥如图所示,若想在B,C之间铺设自来水管道,从节省材料的角度考虑,应选择图中①,②两条路中的哪一条,为什么 如果有人想在桥上较长时间观赏湖面风光,应选择哪条路线 说说你的理由.
【解析】(1)根据过n个点最多可确定条直线,
可得当n=4时,==6(条).
(2)根据两点之间线段最短可知②的长度短,①的长度长.所以从节省材料的角度考虑,应选择②,如果有人想在桥上较长时间观赏湖面风光,应选择①.
【错在哪?】作业错例 课堂实拍
如图,射线OA与射线OB表示的是同一条射线吗 射线AB与射线BA是同一条射线吗
( http: / / www.21cnjy.com )
(1)找错:上面解析过程 (填“有”或“无”)错误.
(2)纠错: .
答案:(1)有
(2)虽然表示射线OA,OB的字母不同,但它们的端点相同,方向一致,是同一条射线;射线AB,BA的端点不同,不是同一条射线.
复习题训练及解析(五)
线段的长短比较
1.比较线段a和b的长短,其结果一定是 ( )
A.a=b B.a>b
C.ab或a=b或a
1.度量法:用刻度尺量出两条线段的长度,再比较长短.
2.叠合法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.
2.根据图形,比较两条线段长度的大小.
(1)线段OA与OB.
答: .
(2)线段AB与AD.
答: .
【解析】(1)由叠合法得OB>OA.
(2)由度量法或圆规截取法得AD>AB.
答案:(1)OB>OA (2)AD>AB
3.如图所示,利用圆规比较图中线段的长短,并用“>”“=”“<”填空.
( http: / / www.21cnjy.com )
(1)AB AC.
(2)AD AC.
(3)AF AC.
(4)AE BC.
(5)BC AB.
【解析】利用圆规比较AB与AC ( http: / / www.21cnjy.com )时,圆规的一支点与A重合,另一支点与C重合,则两张角之间的长度就是AC的长度,保持这个张角,把圆规放在线段AB上,使一支点与A重合,另一支点落在线段AB之间,故AB>AC.用同样的方法可以比较其他几对线段.
答案:(1)> (2)= (3)< (4)< (5)=
4.如图所示,线段a,b,且a>b.
( http: / / www.21cnjy.com )
用圆规和直尺画线段:(1)a+b.(2)a-b.
【解析】(1)画法如图(1),画直线A ( http: / / www.21cnjy.com )F,在直线AF上画线段AB=a,再在AB的延长线上画线段BC=b,线段AC就是a与b的和,记作AC=a+b.
(2)画法如图(2),画直线AF,在直线AF上画线段AB=a,再在线段AB上画线段BD=b,线段AD就是a与b的差,记作AD=a-b.
( http: / / www.21cnjy.com )
5.已知线段a,b,求作线段AB=3a-b.
( http: / / www.21cnjy.com )
【解析】如图:(1)画射线AM.
(2)在射线AM上截取AC,使AC=3a.
(3)在线段AC上截取BC,使BC=b;则线段AB即为所求.
线段的有关计算
1.(2014·山师附中质检)如果线段AB=13cm,MA+MB=17cm,那么下面说法中正确的是 ( )
A.点M在线段AB上
B.点M在直线AB上
C.点M在直线AB外
D.点M可能在直线AB上,也可能在直线AB外
【解析】选D.因为线段AB=13cm,MA+MB=17cm,所以点M可能在线段AB或BA的延长线上,也可能在直线AB外.
2.如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是 ( )
A.CD=AC-BD B.CD=BC
C.CD=AB-BD D.CD=AD-BC
【解析】选B.因为C是线段AB的中点,所以AC=BC,所以CD=BC-BD=AC-BD=AB-BD=AD-AC=AD-BC.
3.判断下列语句中:
①线段AB就是A,B两点间的距离;
②线段AB的一半就是线段AB的中点;
③在所有连结两点的线中直线最短;
④如果AB=BC=CD,则AD=3AB.
其中错误语句的个数是 ( )
A. 0 B. 2 C. 3 D. 4
【解析】选D.线段AB和线段AB的中点都是 ( http: / / www.21cnjy.com )几何图形,而A,B两点间的距离和线段AB的一半都是数量,形与数不能划等号;③把线段与直线的性质混淆了;④中的三条线段可能不在一条直线上,因此,这四个语句都是错误的.
4.线段AD=6cm,线段AC=BD=4cm,E,F分别是线段AB,CD的中点,求线段EF的长.
【解析】因为线段AD=6cm,线段AC=BD=4cm,
所以BC=AC+BD-AD=4+4-6=2cm.
所以AB+CD=AD-BC=6-2=4cm.
又因为E,F分别是线段AB,CD的中点,
所以EB=AB,CF=CD,
所以EB+CF=AB+CD=(AB+CD)=2cm,
所以EF=EB+BC+CF=2+2=4(cm).
【知识归纳】线段的计算
1.线段的长度和有理数一样,可以进行加减等运算.
2.如果题目中没有图形,一定要先画出图形,数形结合思想是数学学习的一种重要方法,应特别注意对线段的中点的灵活运用.
5.如图所示,点C,D为线段AB的三等分点(即分成相等的三等份),点E为线段AC的中点,若ED=9,求线段AB的长度.
【解析】因为C,D为线段AB的三等分点,
所以AC=CD=DB.
又因为点E为AC的中点,则AE=EC=AC,
所以CD+EC=DB+AE.
因为ED=EC+CD=9,
所以DB+AE=EC+CD=ED=9,
则AB=2ED=18.
【错在哪?】作业错例 课堂实拍
已知线段AB=12cm,AB所在的直线上有一点C,且BC=6cm,D是线段AC的中点,求线段AD的长.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错: .
答案:(1)①
(2)本题漏掉了第二种情况:当点C在线段AB的延长线上时,此时AD=
(AB+BC)=(12+6)=9 cm.
复习题训练及解析(六)
角的识别与表示
1.下图中表示∠ABC的是 ( )
( http: / / www.21cnjy.com )
【解析】选C.选项B不是角,用三个大写字母表示角时,中间的字母表示角的顶点.
2.下列关于角的说法中,正确的个数为 ( )
①两条射线所组成的图形叫做角;②角是一条射线从一个位置旋转到另一个位置所组成的图形;③两条射线,它们的端点重合时,可以形成角.
A. 0 B. 1 C. 2 D.3
【解析】选B.①中忽视组成角的两条射线必须有公共点;②中没有确定是否绕着它的端点旋转到另一个位置;③是正确的.
3.(2014·赤峰实验质检)如图所示,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是 ( )
( http: / / www.21cnjy.com )
【解析】选D.∠O是一个单独的大写英文字母,它只能表示独立的一个角,而∠O还可用∠1或∠AOB表示.
4.如图,以O为顶点且小于180°的角一共有多少个
( http: / / www.21cnjy.com )
【解题指南】解答本题的基本思路:
1.先数出以OM为一边的角.
2.再数出以OA,OB…为一边的角.
3.然后把它们加起来.
【解析】7+6+5+4+3+2+1==28.
【方法技巧】确定角的个数
1.数角的个数时必须做到不重不漏.
2.同一个平面内,从一个顶点出发有n条射线时,形成角的个数与一条直线上n个点形成线段的个数类似,为.
5.如图,请指出OA是表示什么方向的一条射线 依照这条射线画出表示下列方向的射线:
( http: / / www.21cnjy.com )
(1)南偏东20°.(2)北偏西50°.(3)东南方向(即南偏东45°).
【解析】OA方向可表示为南偏东65°.(1)(2)(3)如图所示,OB表示南偏东
20°,OC表示北偏西50°,OD表示东南方向.
( http: / / www.21cnjy.com )
角的度、分、秒的换算
1.36.33°可化为 ( )
A.36°30′3″ B.36°33′
C.36°30′30″ D.36°19′48″
【解析】选D.因为0.33×60′=19.8′,0.8×60″=48″,
所以36.33°=36°19′48″.
【易错提醒】要注意进位原则(满60进1)和退位原则(借1当60).
2.在时刻为8:30时,钟表上的时针和分针之间的夹角为 °.
【解析】钟表一周可视为360°,被分成12个大格,每格对应30°.8:30时,时针与分针夹角恰为2.5个格.
故30°×2.5=75°.
答案:75
3.(1)48′= °.(2)39°36′= °.
【解析】(1)48′=48×°=0.8°.
(2)因为36′=36×°=0.6°,所以39°36′=39.6°.
答案:(1)0.8 (2)39.6
4.(2014·新沂实验质检)将26°48′36″用度表示.
【解析】把36″化成分,36″=′×36=0.6′,
48′+0.6′=48.6′,
把48.6′化成度,48.6′=°×48.6=0.81°.
所以26°48′36″=26.81°.
【知识归纳】角的度、分、秒的换算
1.用度、分、秒表示度时,要先把度的小数部分化成分,再把分的小数部分化成秒,用公式1°=60′,1′=60″.
2.用度表示度、分、秒时,要先把秒化成分,再把分化成度,用公式1″=′,
1′=°.
5.(1)把26.29°转化为度、分、秒表示的形式.
(2)把33°24′36″转化成度表示的形式.
【解析】(1)26.29°=26°+0.29°=26°+0.29×60′=26°+17.4′
=26°+17′+0.4×60″=26°17′+24″=26°17′24″.
(2)33°24′36″=33°+24′+36×′=33°+24′+0.6′=33°+24.6′=33°+24.6×°=33.41°.
【变式训练】
(1)1.05°等于多少分 等于多少秒
(2)将70.23°用度、分、秒表示.
【解析】(1)60′×1.05=63′;3600″×1.05=3780″.
所以1.05°等于63′,等于3780″.
(2)将0.23°化为分,可得0.23×60′=13.8′,
再把0.8′化为秒,得0.8×60″=48″.
所以70.23°=70°13′48″.
【错在哪?】作业错例 课堂实拍
写出图中所有小于平角的角.
( http: / / www.21cnjy.com )
(1)错因:
(2)纠错:
答案:(1)以C为顶点的小于平角的角有两个,错解中遗漏一个,且以点C为顶点的角不止一个,不能用顶点处的大写字母表示角.
(2)图中小于平角的角有:∠A,∠B,∠ACB,∠ACD.
复习题训练及解析(七)
角的比较
1.在∠AOB的内部任取一点C,作射线OC,那么有 ( )
A.∠AOC=∠BOC B.∠AOC>∠BOC
C.∠AOC>∠AOB D.∠AOB>∠AOC
【解析】选D.射线OC在∠AOB的内部,那么∠AOC在∠AOB的内部,且有一公共边OA,所以存在∠AOB>∠AOC.
2.如图所示,如果∠AOD>∠BOC,那么下列说法正确的是 ( )
A.∠COD>∠AOB
B.∠AOB>∠COD
C.∠COD=∠AOB
D.∠AOB与∠COD的大小关系不能确定
【解析】选B.因为∠AOD与 ( http: / / www.21cnjy.com )∠BOC中都包含∠BOD,所以都减去它,不等式仍成立,因为∠AOD>∠BOC,所以∠AOD-∠BOD>∠BOC-∠BOD,即∠AOB>∠COD.
3.如图,∠AOB,∠COD都是直角,那么∠DOB与∠AOC的大小关系是∠DOB ∠AOC.
【解析】由题意∠AOB,∠COD都是直角,
所以∠AOD+∠DOB=∠AOC+∠AOD=90°,
所以∠DOB=∠AOC.
答案:=
4.根据图,比较∠AOC,∠BOD,∠BOC,∠COD,∠AOD的大小,它们从小到大排列为 .
【解析】由图可观察出:∠BOC<∠COD;
∠COD<∠BOD;
∠AOD最大;
∠AOC=∠BOD=90°.
答案:∠BOC<∠COD<∠AOC=∠BOD<∠AOD
5.比较大小:直角 锐角;38.51° 38°50′1″.
【解析】直角=90°,锐角大于0°而小于90°.
故直角>锐角;38.51°=38°30′36″<38°50′1″.
答案:> <
角的平分线及相关计算
1.如图,∠AOD-∠AOC= ( )
A.∠ADC B.∠BOC
C.∠BOD D.∠COD
【解析】选D.结合图形,显然∠AOD-∠AOC=∠COD.
2.(2014·襄阳模拟)如图,∠BOC=40°,OD平分∠AOC,∠AOD=25°,那么∠AOB等于 ( )
( http: / / www.21cnjy.com )
A.65° B.50° C.40° D.90°
【解析】选D.因为OD平分∠AOC,∠AOD=25°,
所以∠AOC=2∠AOD=50°,
所以∠AOB=∠AOC+∠BOC=90°.
3.(2013·广州中考)已知∠ABC=30°,BD是∠ABC的平分线,则
∠ABD= .
【解析】∠ABD=∠ABC=×30°=15°.
答案:15°
4.如图,OB是 的角平分线;OC是 的角平分线,
∠AOD= ,∠BOD= .
( http: / / www.21cnjy.com )
【解析】由题意知,OB是∠AOC的角平分线;OC是∠AOD的角平分线,因为
∠COD=30°,所以∠AOD=60°,∠BOD=∠BOC+∠COD=45°.
答案:∠AOC ∠AOD 60° 45°
5.如图,已知∠AOC=∠BOD=75°,∠BOC=30°,则∠AOD= .
( http: / / www.21cnjy.com )
【解析】因为∠AOC=75°,∠BOC=30°,
所以∠AOB=∠AOC-∠BOC=75°-30°=45°,
又因为∠BOD=75°,
所以∠AOD=∠AOB+∠BOD=45°+75°=120°.
答案:120°
6.计算:(1)12°17′×4.
(2)159°52′÷5(精确到分).
【解析】(1)12°17′×4=12°×4+17′×4
=48°+68′=48°+(1°+8′)=49°8′.
(2)159°52′÷5
=159°÷5+52′÷5=31°+4°52′÷5
=31°+(4×60′+52′)÷5
≈31°58′.
【知识归纳】角度的运算
1.角度相加,应是度与度相加,分与分相加,秒与秒相加.但要注意度、分、秒之间的进位是60进制,进位时,60″=1′,60′=1°.
2.角度相减,度与度相减,分与分相减, ( http: / / www.21cnjy.com )秒与秒相减.当分与分相减不够减时,应向度借,当秒与秒相减不够减时,应向分借,借位时,1°=60′,1′=60″.
3.角度与数字相乘,就是用度、分、秒分别与数字相乘,如果满60分要进1度,60秒要进1分.
4.角度除以数字,先用度除以数字,如果 ( http: / / www.21cnjy.com )度有余数,要将度余数乘以60化为分,然后再用分除以数字,若有余数,再把余数乘以60化成秒,再用秒除以数字.并注意题中要求的精确度,进行四舍五入.
7.(2014·巴中实验质检)如图,(1)∠AOC是哪两个角的和.
(2)∠AOB是哪两个角的差.
(3)如果∠AOB=∠COD,那么∠AOC与∠DOB相等吗
( http: / / www.21cnjy.com )
【解析】(1)∠AOC是∠AOB与∠BOC的和.
(2)∠AOB是∠AOC与∠BOC的差,或∠AOB是∠AOD与∠BOD的差.
(3)因为∠AOB=∠COD,
所以∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠DOB.
【知识归纳】对角的和差关系的理解
1.从“形”的方面理解:画一个角等于已知两角的和(或差).
2.从“数”的方面理解:一个角的度数等于已知两个角的度数的和(或差).
【错在哪?】作业错例 课堂实拍
平面内有两个角,∠AOB=50°,∠AOC=20°,OA为两角的公共边,则∠BOC
为 ( )
A.30° B.70°
C.30°或70° D.无法确定
( http: / / www.21cnjy.com )
(1)错因:
(2)纠错:
答案:(1)本题误认为OB,OC在OA的同侧,遗漏OB,OC在OA两侧的情况.
(2)选C.①如图,当OC落在∠AOB的内部时,∠BOC=∠AOB-∠AOC=50°-20°
=30°.
( http: / / www.21cnjy.com )
②如图,当OC落在∠AOB的外部时,
∠BOC=∠AOB+∠AOC=50°+20°=70°.
综上所述,∠BOC为30°或70°.
复习题训练及解析(八)
余角和补角
1.下列说法正确的个数为 ( )
①锐角的补角一定是钝角;
②一个角的补角一定大于这个角;
③如果两个角是同一个角的补角,那么它们相等;
④锐角和钝角互补.
A.1个 B.2个 C.3个 D.4个
【解析】选B.设一个角为∠α,则与它互补 ( http: / / www.21cnjy.com )的角为∠β=180°-∠α.①当∠α为锐角时,∠α<90°,所以∠β>90°,所以∠β为钝角,①正确;②同理,若∠α为钝角,则它的补角∠β为锐角,∠β<∠α,②不正确;③设∠α+∠β=180°,
∠γ+∠β=180°,所以∠α=∠γ,③正确;④中没有明确指出角的值,因此④不正确.故只有①③成立,故选B.
【知识归纳】互余、互补角的特点
1.互余的两个角必须都是锐角.
2.互补的两个角可以一个是锐角另一个是钝角,也可以两个角都是直角.
2.下列图形中,∠1和∠2互为余角的是 ( )
( http: / / www.21cnjy.com )
【解析】选D.由题意知,选项A中∠1与∠2既不互补也不互余,选项B中∠1和∠2互补,选项C中∠1和∠2相等,选项D中∠1和∠2互余.
【变式训练】(2012·长沙中考)下列四个角中,最有可能与70°角互补的
是 ( )
( http: / / www.21cnjy.com )
【解析】选D.70°角的补角=180°-70 ( http: / / www.21cnjy.com )°=110°,是钝角,结合各选项,只有D选项是钝角,所以,最有可能与70°角互补的是D选项的角.
3.(2014·郴州实验质检)一个角的余角比它的补角的少20°,则这个角为
( )
A.30° B.40° C.60° D.75°
【解析】选B.设这个角为x°,则它的余角为(90-x)°,
它的补角为(180-x)°,
根据题意,得90-x=(180-x)-20,
解方程,得x=40.
4.(2013·泰州中考)已知∠α的补角是130°,则∠α= .
【解析】根据互为补角的定义,∠α=180°-130°=50°.
答案:50°
【变式训练】48°16′的补角是 ,
72°39′16″的余角是 .
【解析】48°16′的补角为180°-48°16′=131°44′,
72°39′16″的余角为90°-72°39′16″=17°20′44″.
答案:131°44′ 17°20′44″
5.已知:如图所示,AB是直线,∠BOC=∠AOC=90°,OD,OE是射线,则图中有 对互余的角, 对互补的角.
( http: / / www.21cnjy.com )
【解析】∠AOE与∠EOC,∠BOD与∠COD互余;∠AOE与∠BOE,∠BOD
与∠AOD,∠AOC与∠BOC互补.
答案:2 3
6.如图,O是直线AB上的点,OC是∠AOB的平分线,
( http: / / www.21cnjy.com )
(1)∠AOD的补角是 ,余角是 .
(2)∠DOB的补角是 .
【解析】因为OC是∠AOB的平分线, ( http: / / www.21cnjy.com )所以∠AOC=∠BOC=90°,所以∠AOD的补角是∠BOD,余角是∠COD,∠DOB的补角是∠AOD.
答案:(1)∠BOD ∠COD (2)∠AOD
7.如图,∠AOB是直角,∠COD=90°,OB平分∠DOE,则∠3与∠4是什么关系 并说明理由.
( http: / / www.21cnjy.com )
【解析】∠3=∠4,理由如下:
因为∠AOB是直角,∠COD=90°,
所以∠1+∠2=90°,∠1+∠3=90°,
所以∠2=∠3,
因为OB平分∠DOE,
所以∠2=∠4,所以∠3=∠4.
8.一个角的余角和它的补角之比是3∶7,求这个角的度数.
【解析】设余角为3x°,补角为7x°,
由题意得7x-3x=90,4x=90,x=22.5.
所以这个角为90°-3x°=90°-67.5°=22.5°.
答:这个角的度数为22.5°.
【错在哪?】作业错例 课堂实拍
如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
( http: / / www.21cnjy.com )
(1)指出图中∠AOD与∠BOE的补角.
(2)试说明∠COD与∠COE具有怎样的数量关系.
( http: / / www.21cnjy.com )
(1)错因:
(2)纠错:
答案:(1) (1)中找的补角不全.(2)∠COD与∠COE互余.
(2) (1)∠AOD的补角是∠BOD,∠COD,∠BOE的补角是∠AOE,∠COE.(2)∠COD
与∠COE互余.理由:因为OD平分∠BOC,OE平分∠AOC,所以∠COD=∠BOC,
∠COE=∠AOC,又∠BOC+∠AOC=180°,所以∠COD+∠COE=90°.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
