数学七上第2章有理数复习题及解析

复习题训练及解析（一）
用正负数表示相反意义的量
1.(2013·盐城中考)如果收入50元,记作+50元,那么支出30元记作　(　　)
A.+30元 B.―30元 C.+80元 D.―80元
【解析】选B.支出30元应记作-30元.
2.(2013·济宁中考)一运动员某次跳水的最高点离跳台2m,记作+2m,则水面离跳台10m可以记作　(　　)
A.-10m B.-12m C.+10m D.+12m
【解析】选A.水面离跳台10m可以记作-10m.故选A.
【知识归纳】用正、负数表示相反意义的量两注意
1.用正、负数表示具有相反意义的量,必须是同类量,把一个量记作正数,另一个量记作负数,如果有单位,不要漏单位.
2.用正、负数表示具有相反意义的量时,通常规定某一数值为标准.例如,超出记为正,则不足就记为负.
3.(2014·黄冈模拟)2013年6月 ( http: / / www.21cnjy.com )11日17时38分神舟十号载人飞船在酒泉卫星发射中心成功发射,如果火箭发射点火前5秒记为-5秒,那么火箭发射点火后10秒应记为　(　　)
A.-10秒 B.-5秒 C.+5秒 D.+10秒
【解析】选D.若火箭发射点火前5秒记为-5秒,则点火后为正,那么火箭发射点火后10秒应记为+10秒.
4.(2014·宜昌模拟)长江某水文检测站 ( http: / / www.21cnjy.com ),正常水位是10m,规定高于正常水位记为正,低于正常水位记为负.记录表上有3次记录分别为+1.5,0,-1.6,这三次记录表示的实际水位分别是　　　　　　　　.
【解析】按习惯记录,用正数表示的水位就是高于正常水位;反之,用负数表示的水位就是低于正常水位;0表示刚好是正常水位.
答案:11.5m,10m,8.4m
【易错警示】以正常水位10m为标准,不是以0m为标准.
5.某药品说明书上标明药品保存的温度是(20±2)℃,该药品在　　　　℃范围内保存才合适.
【解析】温度是(20±2)℃,表示最低温度是20℃-2℃=18℃,最高温度是20℃+
2℃=22℃,即18～22℃之间是合适温度.
答案:18～22
【变式训练】某种零件,标明要求是Φ20±0 ( http: / / www.21cnjy.com ).02mm(Φ表示直径,单位:mm),经检查,一个零件的直径是19.9mm,该零件　　　　(填“合格”或“不合格”).
【解析】由Φ20±0.02 ( http: / / www.21cnjy.com )mm可知零件直径最大是20+0.02=20.02(mm),最小是20-0.02=19.98(mm),合格范围在19.98mm和20.02mm之间.因为19.9<19.98,所以不合格.
答案:不合格
有理数的分类
1.(2014·山师大附中质检)下列各数既是正数,又是分数的是(　　)
A.+2 B.0 C.3.5 D.-
【解题指南】分数
【解析】选C.3.5=既是正数,又是分数.
2.下列说法错误的是　(　　)
A.负整数集和负分数集组成负有理数集
B.正整数、零、负整数统称为整数
C.正有理数集与负有理数集组成有理数集
D.3.14是小数,也是分数
【解析】选C.因为正有理数集、零与负有理数集组成有理数集,所以选项C错误.
【知识归纳】分类的三条原则
对概念进行分类要按照一定的原则.例如, ( http: / / www.21cnjy.com )对“人”分类,有多种原则:性别、年龄、籍贯、职业、种族……不同的原则,有不同的分法.对数学知识的分类,一般应遵守以下三条原则:
(1)所分的各类应当互不包含.比如,有理数分为非负有理数、零和非正有理数,就违反了这一原则.因为零既属于非负有理数,又属于非正有理数.
(2)所分各类之和必须是原来的全部.比如,将有理数分为正有理数和负有理数就漏掉了“零”.
(3)必须按同一分类标准进行分类.比如,将有理数分成正有理数、零和负分数,就使得各类间的关系含糊不清.
3.(2012·玉林中考)既不是正数也不是负数的是　　　　　　.
【解析】既不是正数也不是负数的数是0.
答案:0
【知识拓展】对数“0”的认识
(1)0并不都表示“没有”的意义,“0”还具有确定的含义.
(2)“0”既不是正数,也不是负数,它是整数.
(3)“0”是划分正数和负数的界限,同时也是各类相反意义的量的基准.
(4)“0”具有独特的运算法则,如任何数与0相乘,积都是0.
4.将下列各数分别填入相应的大括号里:5,-,2014,-0.02,0.618,0,-,-13,,-2.
正数集:{　　　　　　　　　　…};
整数集:{　　　　　　　　　　…};
负数集:{　　　　　　　　　　…};
分数集:{　　　　　　　　　　…};
自然数集:{　　　　　　　　　　…};
负整数集:{　　　　　　　　　　…}.
【解题指南】有理数的分类
有理数按定义可分为:
有理数
有理数按正负分为:
有理数
不论哪种分类标准,都要做到不重复,不遗漏.
【解析】正数集:;
整数集:{5,2014,0,-13,-2…};
负数集:;
分数集:;
自然数集:{5,2014,0…};
负整数集:{-13,-2…}.
5.把-6,0.3,,9,-分成两类,使两类的数具有不同的特征,写出你的分法.
【解析】方法一:可分为整数和分数两类,其中-6,9属于整数,0.3,,-属于分数.
方法二:可分为正数和负数两类,其中0.3,,9属于正数,-6,-属于负数.(答案不唯一,其他分法合理均可)
【知识归纳】分数和有理数的关系
1.凡是分数都是有理数.
2.有限小数和无限循环小数都可化为分数,所以是有理数;无限不循环小数不能化为分数,所以不是有理数.
【错在哪？】作业错例 课堂实拍
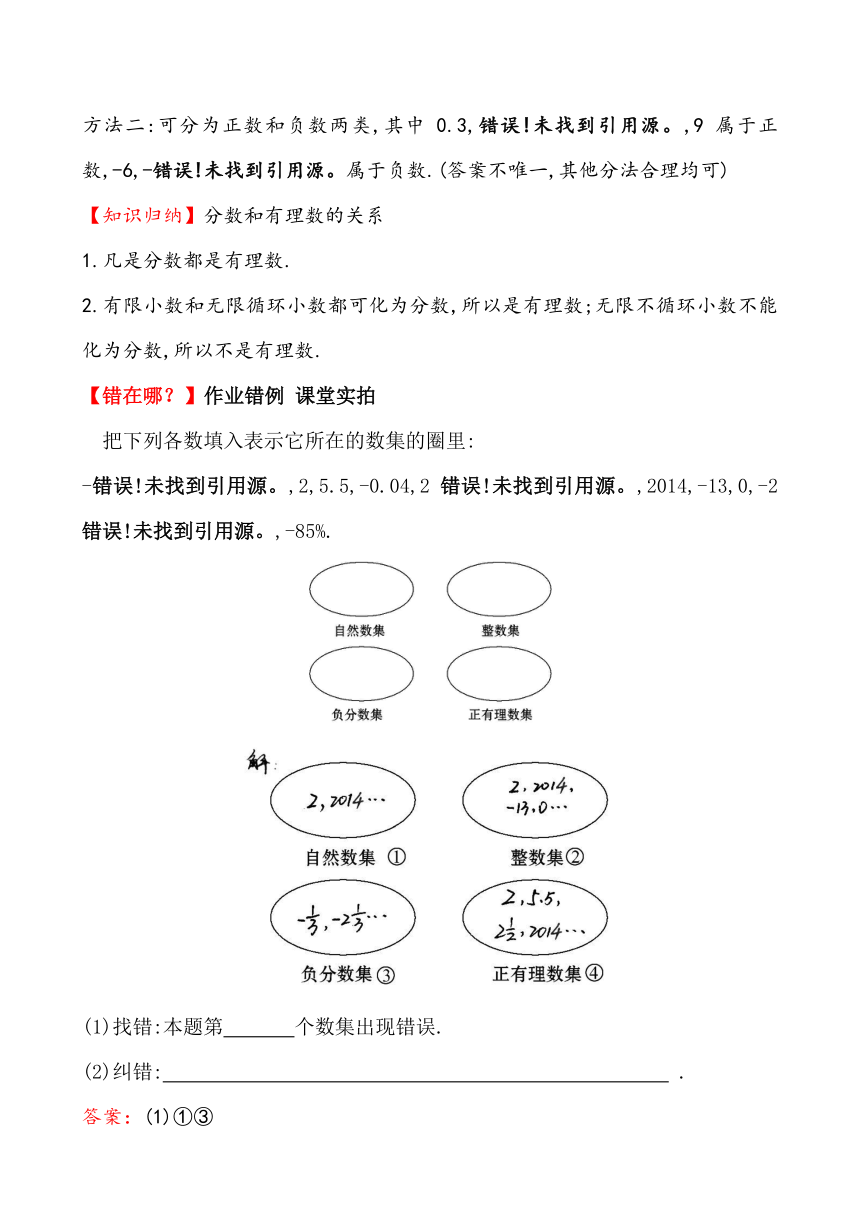
　把下列各数填入表示它所在的数集的圈里:
-,2,5.5,-0.04,2,2014,-13,0,-2,-85%.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)找错:本题第 个数集出现错误.
(2)纠错: .
答案：(1)①③
(2)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
复习题训练及解析（二）
数轴上的点与有理数的关系
1.下列表示数轴的图形中正确的是　(　　)
( http: / / www.21cnjy.com )
【解题指南】数轴需具备三要素:
(1)原点:通常表示0.(2)正方向:水平的数轴通常取向右的方向为正方向.(3)单位长度:以合适的长度作为单位长度,三者缺一不可.
【解析】选D.根据数轴的三要素——原点、正方向、单位长度可知,选项D中的图形是数轴.
2.(2014·新疆模拟)如图所示,点M表示的数是　(　　)
A.2.5　　　　B.-1.5　　　　C.-2.5　　　　D.1.5
【解析】选C.由数轴得点M位于-2和-3的正中间,所以点M表示的数是-2.5.
3.如图,在数轴上表示到原点的距离为3个单位长度的点有　(　　)
A.D点 B.A点 C.A点和D点 D.B点和C点
【解析】选C.由数轴与题意可得,在数轴上表示到原点的距离为3个单位长度的点有A点和D点.
【变式训练】数轴上的点A到表示-1的点的距离是6个单位长度,则点A表示的数为　(　　)
A.6或-6　　　B.-7　　　C.5　　　D.5或-7
【解析】选D.与表示-1的点的距离为6个单位长度的点有两个,分别在表示-1的点的左边和右边.
4.在数轴上,表示+2的点在原点的 ( http: / / www.21cnjy.com )　　　　侧,距原点　　　　个单位长度;表示-7的点在原点的　　　　侧,距原点　　　　个单位长度;两点之间的距离为
　　　　个单位长度.
【解析】在数轴上,表示+2的点在原 ( http: / / www.21cnjy.com )点的右侧,距原点2个单位长度;表示-7的点在原点的左侧,距原点7个单位长度;两点之间的距离为9个单位长度.
答案:右　2　左　7　9
【知识拓展】数形结合思想
(1)数学中,常常把实际问题转化为数学模型,需把具体的人或事物抽象成点或线,用图的形式表达过程,找到隐含的数量关系,达到数形结合的目的.
(2)数轴是进入初中后所接触的第一个数形结合的工具,它把数与形有机结合起来,在处理一些问题时更形象,更直观.
5.数轴上与表示+2的点距离是3个单位长度的点表示的数是　　　　.
【解析】在数轴上,与表示+2的点距离是3个单位长度的点有两个,分别位于已知点的两侧,于是得到所表示的数是+5或-1.
答案:+5或-1
【易错提醒】只考虑+2右边距离是3个单位长度的点所表示的数,遗漏+2左边距离是3个单位长度的点所表示的数.
6.先在数轴上画出表示下列各数的点,然后按照数轴上从左到右的顺序,将这些数重新排列:
-2,-1,-2,,-0.5,0,4.5.
【解析】表示这些数的点在数轴上表示为:
将这些数按照数轴上从左到右的顺序重新排列为:
-2,-2,-1,-0.5,0,,4.5.
【知识归纳】用数轴上的点表示有理数时的三点注意:
1.不要漏掉画正方向.
2.单位长度要均匀相等,切不可大小不一.
3.负数的位置确定要三思,不要写错位置.
有理数的大小比较
1.(2013·重庆中考)在-2,0,1,-4这四个数中,最大的数是　(　　)
A.-4 B.-2 C.0 D.1
【解析】选D.根据有理数比较大小的法则“正数都大于零,负数都小于零,正数都大于负数”,易知1最大.
2.如图,数轴上A,B,C,D四点表示的数分别为a,b,c,d,则它们的大小关系是
　(　　)
A.a>b>c>d B.c>a>d>b
C.a>c>d>b D.a>c>b>d
【解析】选C.由于数轴上表示的数,右边的数大于左边的数,因此a>c>d>b.
3.比较大小:-2　　　4(填“>”或“<”).
【解析】由负数都小于正数得-2<4.
答案:<
4.如图,请你把这五个数:+6,-4.5,,-5,0,按从大到小,从左到右串成糖葫芦状,写在○内的数字依次为:　　　　　　　　　　.
【解析】把这五个数表示在数轴上为:
从大到小的数字依次为+6,,0,-4.5,-5.
答案:+6,,0,-4.5,-5
【变式训练】将三个数-,-0.331,-按从大到小排列起来是　　　　.
【解析】把-,-0.331,-表示在数轴上为:
( http: / / www.21cnjy.com )
按由大到小的顺序排列起来是-0.331,-,-.
答案:-0.331,-,-
5.在数轴上点A,B,C,D,E,F,G分别表示下列各数:
3.5,-3.5,0,2,-2,-,0.5.
(1)按从小到大的顺序用“<”把这些数连接起来.
(2)A与B,D与E,F与G之间分别有怎样的位置关系
【解析】(1)各数用数轴上的点表示,如图所示:
( http: / / www.21cnjy.com )
根据数轴上右边的数总比左边的数大,各数的大小关系按从小到大的顺序用“<”连接为:-3.5<-2<-<0<0.5<2<3.5.
(2)观察数轴可知A与B,D与E,F与G到原点的距离都分别相等.
【错在哪？】作业错例 课堂实拍
　先在数轴上画出表示下列各数的点,然后利用数轴比较它们的大小:,3,2.5,-1.5,-2.5,1,0.
( http: / / www.21cnjy.com )
(1)错因: .
(2)纠错: .
答案：(1) -1.5和-2.5在数轴上所标的位置错误.
(2)将这些数分别在数轴上表示出来,如图所示:
复习题训练及解析（三）
求一个数的相反数
1.(2013·六盘水中考)-2013的相反数是　(　　)
A.-2013　　　 B.　　 　C.2013　　　 D.-
【解析】选C.方法一:因为负数的相反数是正数,
所以-2013的相反数是2013,故选C.
方法二:因为-2013的相反数可以表示为-(-2013),
所以-(-2013)=2013,故选C.
2.下列各组数中,互为相反数的是　(　　)
A.3和-3 B.-3和
C.-3和- D.和3
【解题指南】判断互为相反数两看
【解析】选A.3和-3是只有正负号不同的两个数.
3.如图,数轴上表示数2的相反数的点是　(　　)
( http: / / www.21cnjy.com )
A.点P B.点Q C.点M D.点N
【解析】选D.因为2的相反数是-2,数-2在数轴上的对应位置为点N.
【互动探究】数轴上点M与点Q表示的数有什么关系
提示:点M表示的数为-,点Q表示的数为,因为-与互为相反数,所以点M与点Q表示的数互为相反数.
4.如果a与2014互为相反数,那么a=　　　　.
【解析】如果a与2014互为相反数,那么a是2014的相反数,所以a=-2014.
答案:-2014
【变式训练】-2014的相反数是　　　　.
【解析】只有正负号不同的两个数互为相反数,所以-2014的相反数是2014.
答案:2014
5.数轴上表示一个数的点距离原点2个单位长度,且在原点的左边,则这个数的相反数是　　　　.
【解析】因为一个数在数轴上表示的点距原点2个单位长度,且在原点的左边,所以这个数是-2,所以它的相反数是2.
答案:2
【知识归纳】“相反数”与“相反意义的量”的区别
认为相反意义的量是带“单位”的相反数是错误的.“相反数”与“相反意义的量”主要区别在于:
(1)相反意义的量包含两层意思:
①两个量意义相反、符号不同;
②它们都表示一定的数量(在数量上它们不一定相同).
(2)相反数:
①两个数正负号不同;
②两个数除正负号不同外,其余完全相同.
6.写出下列各数的相反数,并在数轴上把这些相反数表示出来:+2,-3,0,-(-1),-3.5,-(+2).
【解析】因为只有正负号不同的两个数叫互为相反 ( http: / / www.21cnjy.com )数,所以+2,-3,0,-(-1),-3.5,-(+2)的相反数分别是:-2,+3,0,-1,+3.5,+2,在数轴上表示为:
多重符号的化简
1.下列化简错误的是　(　　)
A.-(-3)=3
B.+(-3)=-3
C.-[-(+3)]=-3
D.+{-[+(-3)]}=3
【解析】选C.-[-(+3)]=-(-3)=3.
2.在+(-2)与-2,- ( http: / / www.21cnjy.com )(+1)与+1,-(-4)与+(-4),-(+5)与+(-5),-(-6)与+(+6),+(+7)与+(-7)几对数中,互为相反数的有　(　　)
A.3对　　　 B.4对　　　 C.5对　　 　D.6对
【解析】选A.+(-2)=-2与-2,-(+5)=-5与+(-5)=-5,-(-6)=6与+(+6)=6都分别相等,而-(+1)=-1与+1,-(-4)=4与+(-4)=-4,+(+7)=7与+(-7)=-7都分别互为相反数.
3.(2013·晋江中考)化简-(-2)=　　　　.
【解析】-(-2)表示的是-2的相反数,-2的相反数是2,所以-(-2)=2.
答案:2
4.假期里,小亮做这样一道题:“化简:”,其中的“+”或“-”被调皮的小妹用墨水涂上了,他翻开后面的答案得到结果等于-10,聪明的小亮把此题所有可能出现的情况都写了出来.你知道他写了哪些式子吗
【解析】由式子可以看出,原题应该有三个符号.由结果可知负号的个数应是奇数.所以原式子所有可能出现的情况为:
-[-(-10)]或-[+(+10)]或+[-(+10)]或+[+(-10)].
【错在哪？】作业错例 课堂实拍
　画出数轴,在数轴上表示下列各数的相反数,并把它们的相反数按照数轴上从左到右的顺序排列:1,-(+2.5),0,-3.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错: .
答案：(1)①
(2) 1的相反数是-1,因为-(+2 ( http: / / www.21cnjy.com ).5)=-2.5,所以-(+2.5)的相反数是2.5,0的相反数是0,-3的相反数是3.把它们的相反数在数轴上表示为:
它们的相反数在数轴上从左到右的顺序是:-1,0,2.5,3.
复习题训练及解析（四）
求一个数的绝对值
1.(2013·海南中考)-5的绝对值是　(　　)
A. B.-5 C.5 D.-
【解析】选C.因为-5是一个负数,它的绝对值等于它的相反数,而-5的相反数是5,所以-5的绝对值是5.故选C.
2.(2013·黔西南州中考)|-3|的相反数是　(　　)
A.3 B.-3 C.±3 D.
【解题指南】解答本题两步骤:(1)求出|-3|的值.
(2)求其相反数.
【解析】选B.因为|-3|=3,
所以3的相反数是-3.故选B.
【变式训练】如果x与2互为相反数,那么|x-1|等于　(　　)
A.1 B.-2 C.3 D.-3
【解析】选C.因为x与2互为相反数,
所以x=-2,
那么|x-1|=|-2-1|=3.
3.(2013·桂林中考)下列各数是负数的是　(　　)
A.0 B.-2 013 C.|-2 013| D.
【解析】选B.A选项中的0既不是正数也不是负数,不符合题意;B选项中的-2013是负数,符合题意;C选项中,|-2013|=2013,是正数,不符合题意;D选项中的是正数,不符合题意.故选B.
4.(2014·丽水模拟)如图,数轴的单位长度为1,如果点A,B表示的数的绝对值相等,那么点A表示的数是　(　　)
A.-4 B.-2 C.0 D.4
【解析】选B.设A,B表示的数分别为a,b,则|a|=|b|=2,又因为a5.求下列各数的绝对值:
(1)-8.(2)0.27.(3)-7.(4)+.
【解析】(1)|-8|=8.
(2)|0.27|=0.27.
(3)|-7|=7.
(4)|+|=.
绝对值的性质及应用
1.若|x|=5,则x的值是　(　　)
A.5 B.-5 C.±5 D.
【解析】选C.因为|x|=5,即数x到原点的距离是5,而到原点的距离是5的数有5和-5,所以x的值是±5.
【易错提醒】绝对值等于一个正数的数有两个,它们互为相反数,易漏掉其中一个.
【知识归纳】绝对值的性质
(1)任何有理数都有绝对值,且只有一个.
(2)由绝对值的几何定义可知,数的绝对值是数轴上两点间的距离,因此,任何一个数的绝对值都是非负数.
(3)互为相反数的两个数的绝对值相等.
(4)绝对值相等的两个数相等或互为相反数.
2.(2014·永州模拟)已知a为有理数,则下列四个数中一定为非负数的是
　(　　)
A.a B.-a C.|-a| D.-|-a|
【解析】选C.选项A中的a可以表示任何 ( http: / / www.21cnjy.com )有理数;选项B中的-a表示a的相反数,所以也是表示任何有理数;选项C中|-a|表示-a的绝对值,根据绝对值的意义,可知|-a|为非负数;选项D中-|-a|表示|-a|的相反数,由于|-a|为非负数,所以-|-a|为非正数.
3.绝对值大于3且小于7的所有整数有　　　　.
【解析】绝对值大于3且小于7的所有整数是:-4,-5,-6,4,5,6.
答案:-4,-5,-6,4,5,6
4.已知|a-3|+|b-2|=0,求|a+b|的值.
【解题指南】解答本题两个关键:
(1)利用绝对值的非负性(若|a|+|b|=0,则a=0且b=0)求出字母的值.
(2)代入式子求值.
【解析】由题意知,|a-3|=0,|b-2|=0,
解得a=3,b=2,
所以|a+b|=5.
【错在哪？】作业错例 课堂实拍
　已知|x|=-(-2),求x的值.
( http: / / www.21cnjy.com )
(1)找错:第 步出现错误.
(2)纠错: .
答案：(1)②
(2)因为|x|=-(-2),所以|x|=2,因为|±2|=2,所以x=±2.
复习题训练及解析（五）
有理数的大小比较
1.(2013·桂林中考)在0,2,-2,这四个数中,最大的数是　(　　)
A.2 B.0 C.-2 D.
【解析】选A.因为在0,2,-2,这四个数中,只有2和是正数,且2>,所以最大的数是2.故选A.
2.(2014·桂林模拟)比较-,-,的大小,结果正确的是　(　　)
A.-<-< B.-<<-
C.<-<- D.-<-<
【解析】选A.在-,-,这三个数中,是正数,-和-是负数,正数大于负数,所以最大,>,所以-<-,故选A.
3.下面是几个城市某年一月份的平均温度,其中平均温度最低的是　(　　)
A.桂林11.2℃ B.广州13.5℃
C.北京-4.8℃ D.南京3.4℃
【解析】选C.因为13.5>11.2>3.4>-4.8,所以平均温度最低的是北京-4.8℃.
4.(2013·西双版纳中考)若a=-,b=-,则a,b的大小关系是a　　　b(填:“>”“<”或“=”).
【解析】因为>,所以-<-,所以a答案:<
【变式训练】比较-和-的大小.
【解析】因为==,==,<,所以->-.
5.写出绝对值大于2小于5的所有整数,并比较它们的大小.
【解题指南】已知一个数的绝对值求这个数,根据绝对值的几何意义去分析,即绝对值等于一个正数的数有两个,它们互为相反数;绝对值为0的数只有0.
【解析】绝对值等于2的整数是±2, ( http: / / www.21cnjy.com )绝对值等于5的整数是±5,所以绝对值大于2小于5的整数在-5～-2和2～5之间.绝对值大于2小于5的整数有3,4,-3,-4,它们的大小关系为:-4<-3<3<4.
6.比较下列每对数的大小:
(1)-(-5)与-|-5|.
(2)-(+3)与0.
(3)-π与-|-3.14|.
【解析】(1)化简得:-(-5)=5,-|-5|=-5.
因为正数大于一切负数,所以-(-5)>-|-5|.
(2)化简得:-(+3)=-3.因为负数小于零,
所以-(+3)<0.
(3)化简得:-|-3.14|=-3.14.这是两个负数比较大小.
因为|-π|=π,|-3.14|=3.14,而π>3.14,
所以-π<-|-3.14|.
【知识归纳】含有括号的有理数的大小比较
(1)比较含有括号(或绝对值符号)的有理数的大小时,先将原数进行化简.
(2)确定属于“正数与正数,正数与负数,正数与0,负数与0,负数与负数”哪一类.
(3)根据相应的法则进行大小比较.
【变式训练】比较下列各对数的大小:
(1)+(-8.1)与|-8.1|.
(2)-(+0.01)与0.
(3)-与-.
(4)-与-.
【解析】(1)+(-8.1)=-8.1,|-8.1|=8.1,因为正数大于负数,所以8.1>-8.1.
即+(-8.1)<|-8.1|.
(2)-(+0.01)=-0.01,
因为0大于负数,所以-0.01<0,即-(+0.01)<0.
(3)-=4>0,-=-<0,
因为正数大于负数,所以4>-,
即->-.
(4)==;==.
因为>,即>,
所以-<-.
借助数轴比较有理数的大小
1.如图,数轴上A,B,C三点表示的数分别为a,b,c,则它们的大小关系是　(　　)
A.a>b>c B.b>c>a
C.c>a>b D.b>a>c
【解析】选D.根据数轴的方向“右边的数>左边的数”,因此b>a>c.
2.有理数m,n在数轴上的位置如图所示,比较大小:-m　　　-n.
【解析】观察数轴可知m<0,n<0,|m|>|n|,所以-m>-n.
答案:>
3.有理数a,b在数轴上位置如图所示,则|a|,|b|的大小关系是　　　　.
【解析】在数轴上,|a|就是实数a所对应的点与原点的距离.|b|就是实数b所对应的点与原点的距离.观察数轴得|a|>|b|.
答案:|a|>|b|
【知识归纳】利用数轴比较有理数的大小的方法
　　利用数轴比较两个有理数的大小,数轴右边点表示的数总比左边点表示的数大,且正数大于0,0大于负数,负数小于正数.
4.如图,数轴的一部分被墨水污染,被污染的部分所有整数用“<”连接起来为　　　　.
【解析】被墨水污染的整数在数轴上从左到右分别是-3,-2,-1,0,1,用“<”连接起来为-3<-2<-1<0<1.
答案:-3<-2<-1<0<1
【易错提醒】不要漏掉整数“0”.
5.在数轴上表示数4,-2,1,0,-2.5,并比较它们的大小,将它们按从小到大的顺序用“<”连接.
【解析】在数轴上表示数4,-2,1,0,-2.5,如图:
按从小到大的顺序用“<”连接:-2.5<-2<0<1<4.
【方法技巧】比较有理数大小的五种方法
(1)法则比较法:有理数大小的比较法则有:①正数都大于零,负数都小于零,正数大于负数.②两个负数,绝对值大的反而小.
(2)数轴比较法:在数轴上表示的几个数,右边的数总比左边的数大,根据这个特点可把需要比较的数表示在数轴上,通过数轴比较数的大小.
(3)特殊值比较法:含有字母的数的比较,通常采用取特殊值法,简单快捷.
(4)分类讨论法:比较含有字母的数的大小,有时按照字母的取值范围大于零、等于零或小于零进行讨论,再进行比较,体现了分类讨论的数学思想.
(5)求差(商)法:随着进一步学习有理数的运算,可以知道比较有理数的方法还有求差法、求商法.
【错在哪？】作业错例 课堂实拍
比较-与-的大小.
( http: / / www.21cnjy.com )
(1)找错:第 步出现错误.
(2)纠错: .
答案：(1)③
(2) 因为, ,而,即,所以 (两个负数，绝对值大的反而小)
复习题训练及解析（六）
有理数的加法
1.(2013·天津中考)计算(-3)+(-9)的结果是　(　　)
A.12 B.-12 C.6 D.-6
【解析】选B.(-3)+(-9)=-(3+9)=-12.
2.(2013·包头中考)计算(+2)+(-3)所得的结果是　(　　)
A.1 B.-1 C.5 D.-5
【解析】选B.(+2)+(-3)=-(3-2)=-1.
3.在1,-1,-2这三个数中,任意两数之和最大的是　(　　)
A.2 B.0 C.-1 D.-3
【解题指南】解答本题的两个步骤:
(1)先求出所有的任意两数之和.
(2)再根据有理数大小比较的法则找出任意两数之和中最大的数.
【解析】选B.因为1+(-1)=0,1+(-2)=-1,(-1)+(-2)=-3,所以任意两数之和最大的是0.
4.计算:(1)(-4)+(-5)=　　　　.
(2)+=　　　　.
(3)(-0.125)+=　　　　.
(4)0+(-9.7)=　　　　.
【解析】(1)(-4)+(-5)=-(4+5)=-9.
答案:-9
(2)+=-=-.
答案:-
(3)(-0.125)+=+=0.
答案:0
(4)0+(-9.7)=-9.7.
答案:-9.7
【方法技巧】巧记有理数加法法则
两数相加很重要,计算处处要用到.
学好法则是关键,关键是要看符号.
法则分为同异号,同号异号要分好.
符号不变取原号,正取正来负取负.
别忘绝对值相加,这样求来不会错.
异号相加大减小,符号小心确定好.
绝大取号定正负,互为相反没符号.
5.计算:(1)+.(2)0+.
【解析】(1)+=-=-=-1.
(2)0+=-.
【方法技巧】有理数的加法运算口诀:同号相加一边倒;异号相加“大”减“小”,符号跟着大的跑;绝对值相等“零”正好.
注:“大”减“小”是指绝对值的大的减小的.
有理数加法的实际应用
1.北京与巴黎两地的时差是-7小时(带正号的数表示同一时间比北京早的时间数),如果现在北京时间是7:00,那么巴黎的时间是　(　　)
A.0:00　　　　B.7:00　　　　C.14:00　　　　D.21:00
【解析】选A.根据题意得:7+(-7)=0,所以巴黎的时间是0:00.
【变式训练】纽约时间比香港时间迟13小时 ( http: / / www.21cnjy.com ).你与一位在纽约的朋友约定,纽约时间4月1日晚上8时与他通话,假若你在香港应　　　月　　　日　　　时给他打电话.
【解析】晚上8时即20时,20+13=33(时),33-24=9,即4月2日早上9时.
答案:4　2　早上9
2.(2014·哈尔滨模拟)一天早晨的气温是-7℃,中午的气温比早晨上升了11℃,中午的气温是　(　　)
A.11℃ B.4℃ C.18℃ D.-11℃
【解析】选B.中午的气温是-7+11=4(℃).
3.(2013·峨眉山实验质检)乐乐家冰箱冷冻室的温度为-15℃,调高3℃后的温度为　(　　)
A.18℃ B.12℃ C.-12℃ D.-18℃
【解析】选C.根据题意得-15+3=-12(℃).
4.水位上升8cm,又下降13cm,则水位上升的结果是　　　　cm.
【解析】由题意得(+8)+(-13)=-5(cm).
答案:-5
【互动探究】若改为“水位下降8cm,又下降13cm”,则水位上升的结果是
　　　　cm.
提示:由题意得(-8)+(-13)=-21(cm).
答案:-21
5.A地海拔-50m,B地比A地高90m,B地海拔　　　　.
【解析】因为A地海拔-50m,B地比A地高90m,所以B地海拔(-50)+90=40(m).
答案:40m
6.在一次水下机器人测试中,机器人在 ( http: / / www.21cnjy.com )海下时而上升,时而下降.机器人的初始位置在海平面下1500m,下面是机器人在某段时间内的运动情况(把上升记为“+”,下降记为“-”,单位:m):-2800,1600.问:现在机器人处在什么位置
【解析】根据题意可得:上升为“+”,下降为“-”;则现在机器人的位置距初始位置的距离是(-2800)+1600=-1200(m).
故(-1200)+(-1500)=-2700(m).
答:机器人现在处在海平面下2700m处.
【错在哪？】作业错例 课堂实拍
　计算:+.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错: .
答案：(1)② (2)
复习题训练及解析（七）
加法运算律的运用
1.下面计算用的加法运算律是　(　　)
+3.2++7.8=+(3.2+7.8)=-1+11=10
A.交换律
B.结合律
C.先用交换律,再用结合律
D.先用结合律,再用交换律
【解析】选C.原式=++3.2+7.8(交换律)
=+(3.2+7.8)(结合律)
=-1+11=10.
2.(2014·威海模拟)计算33+(-32)+7+(-8)的结果为　(　　)
A.0　　　　　B.2　　　　　C.-1　　　　　D.5
【解析】选A.33+(-32)+7+(-8)
=(33+7)+[(-32)+(-8)]
=40+(-40)=0.
3.三个小球上的有理数之和等于　　　　.
【解析】(-8)+(+10)+(-2)=[(-8)+(-2)]+(+10)=(-10)+(+10)=0.
答案:0
4.计算:++++的正确结果是　　　　.
【解析】++++
=++
=+(-1)+0=-.
答案:-
5.绝对值小于2014的所有整数有　　　　个,它们的和是　　　　.
【解析】绝对值小于2014的整数有-2013,-2012,-2011,…,0,…,2011,2012,
2013共4027个,它们的和为-2013+(-2012)+(-2011)+…+0+…+2011+2012+2013
=[(-2013)+2013]+[(-2012)+2012]+[(-2011)+2011]+…+0=0.
答案:4027　0
【易错提醒】不要漏掉整数0.
【变式训练】绝对值大于5且小于10的所有整数的和为　　　　.
【解析】绝对值大于5且小于10的所有整数有:
±6,±7,±8,±9,它们的和为0.
答案:0
6.计算下列各题:
(1)+++.
(2)0.75+++1.25.
【解析】
(1)+++
=+
=-+=-.
(2)0.75+++1.25
=(0.75+1.25)+
=2+=-4.
【知识归纳】有理数加法运算的六种简便方法
1.互为相反数结合法:由于互为相反数的两个数的和为0,因此把互为相反数的加数相结合计算较为简便.
2.同号结合法:把正数与正数、负数与负数分别相加计算较为简便.
3.同形结合法:整数与整数、小数与小数、同分母的分数与同分母的分数分别相加计算较为简便.
4.转化结合法:由于在同一个算式中既有分数又有小数,一般要先统一,具体统一成分数还是小数,这要看哪一种运算更简便,不能一概而论.
5.凑整结合法:把相加得整数的加数先结合.
6.凑零结合法:可先分别把相加得零的部分加数相加,然后再计算.
有理数加法的实际应用
1.在CCTV“开心辞典”栏目中,主持 ( http: / / www.21cnjy.com )人问这样一道题目:“a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,请问:a,b,c三数之和是”　(　　)
A.-1 B.0 C.1 D.2
【解题指南】解答本题两关键:
(1)首先根据最小正整数、最大负整数、绝对值最小的有理数的意义求出a,b,c的值.
(2)把a,b,c的值代入a+b+c求出答案.
【解析】选B.由题意,得:a=1,b=-1,c=0,a+b+c=1+(-1)+0=0.
2.某商店去年四个季度的盈亏情 ( http: / / www.21cnjy.com )况如下(盈余为正):+128.5万元,-140万元,-95.5万元,+280万元,这个商店的总盈利情况是　(　　)
A.盈余644万元
B.亏本173万元
C.盈余173万元
D.亏本64万元
【解析】选C.(+128.5)+(-140)+(-95.5)+(+280)
=(128.5+280)+[(-140)+(-95.5)]
=408.5+(-235.5)
=408.5-235.5
=173(万元).
【变式训练】七年级(1)班一学期班费收 ( http: / / www.21cnjy.com )支情况如下(收入为正,支出为负):+250元,-55元,-120元,+7元.该班期末时班费结余为　(　　)
A.82元　 　 B.85元　　 C.90元　　 D.95元
【解析】选A.250+(-55)+(-120)+7
=250+7+[(-55)+(-120)]
=257+(-175)=82(元).
3.现有10箱苹果梨,称重记录如下(单位:kg):31,29,28.5,31.8,29.5,
29.5,32,32.5,28.2,32.3,求这10箱苹果梨的总质量.
【解析】若超过30kg的数记作正数,不足3 ( http: / / www.21cnjy.com )0kg的数记作负数,则这10箱苹果梨的质量记作(单位:kg):+1,-1,-1.5,+1.8,-0.5,-0.5,+2,+2.5,-1.8,+2.3.
所以(+1)+(-1)+(-1.5)+(+1.8)+(-0.5)+(-0.5)+(+2)+(+2.5)+(-1.8)+(+2.3)
=[1+(-1)]+[(+1.8)+(-1.8)]+[(-1.5)+(-0.5)+(-0.5)+2.5]+2+2.3
=4.3(kg).
30×10+4.3=304.3(kg).
答:这10箱苹果梨的总质量为304.3kg.
【错在哪？】作业错例 课堂实拍
出租车司机小李某天下午的营运 ( http: / / www.21cnjy.com )全是在东西方向的大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:km)如下:+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6.
(1)将最后一名乘客送到目的地时,小李当天下午行车里程是多少
(2)若汽车耗油量为0.1L/km,这天下午小李共耗油多少L
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:
答案：(1)①
(2)|+15|+|-2|+|+5|+|-1|+|+10|+|-3|+|-2|+|+12|+|+4|+|-5|+|+6|
=65(km).
答:小李当天下午行车里程是65km.
共耗油:65×0.1=6.5(L).
答:这天下午小李共耗油6.5L.
复习题训练及解析（八）
有理数的减法运算
1.(2013·柳州中考)计算-10-8所得的结果是　(　　)
A.-2　　　 B.2　　 　
C.18　　 　 D.-18
【解析】选D.-10-8=-10+(-8)=-18.
2.计算-,正确的结果为　(　　)
A. B.-
C. D.-
【解析】选D.-=-=-.
3.(2013·梧州中考)计算:0-7=　　　　.
【解析】0-7=0+(-7)=-7.
答案:-7
4.计算:(1)(-3)-(+7).　　(2)-.
(3)-. (4)0-(-5).
【解析】(1)(-3)-(+7)=(-3)+(-7)=-10.
(2)-=+=.
(3)-=+=-3.
(4)0-(-5)=0+5=5.
【知识归纳】有理数减法三注意
(1)计算有理数的减法时应先弄清减数的符号是“+”还是“-”.
(2)将有理数的减法转化为加法时,要先同时改变两个符号,将运算符号“-”变成“+”,同时要改变性质符号.
(3)将减法统一成加法运算后,可以根据加法的运算律简化计算.
【变式训练】计算:(1)(-3)-(-1).(2)(-7)-0.
(3)12-21.(4)(-1.7)-(-2.5).
【解析】(1)(-3)-(-1)=(-3)+(+1)=-2.
(2)(-7)-0=(-7)+0=-7.
(3)12-21=12+(-21)=-9.
(4)(-1.7)-(-2.5)=(-1.7)+(+2.5)=0.8.
5.计算:
(1)(+5)-(-3).　　　 (2)(-3)-(+2).
(3)(-20)-(-12). (4)(-1.4)-2.6.
(5)-. (6)-.
【解析】(1)(+5)-(-3)=5+3=8.
(2)(-3)-(+2)=(-3)+(-2)=-5.
(3)(-20)-(-12)=(-20)+(+12)=-8.
(4)(-1.4)-2.6=(-1.4)+(-2.6)=-4.
(5)-=+=1.
(6)-=+
=+=.
有理数减法的应用
1.(2013·曲靖中考)某地某天的最高气温是8℃,最低气温是-2℃,则该地这一天的温差是　(　　)
A.-10℃　　　　 B.-6℃　　　　
C.6℃　　　　 D.10℃
【解析】选D.因为温差=最高气温-最低气温,所以温差=8-(-2)=8+2=10(℃).
2.珠穆朗玛峰的海拔高度约为8844m,马里亚纳海沟的最低点的海拔高度为-11000m,则珠穆朗玛峰比马里亚纳海沟的最低点高　(　　)
A.2156m B.19844m
C.-2156m D.-19844m
【解析】选B.8844-(-11000)=8844+11000=19844(m).
【变式训练】甲、乙、丙三地的海拔高度分别是20m,-15m,-5m,那么最高的地方比最低的地方高　　　　m.
【解析】最高的地方比最低的地方高20-(-15)=35(m).
答案:35
3.某粮店出售三种品牌的面粉的袋上,分 ( http: / / www.21cnjy.com )别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差　(　　)
A.0.8kg
B.0.6kg
C.0.5kg
D.0.4kg
【解析】选B.0.3-(-0.3)=0.3+0.3=0.6(kg).
4.某地一周内每天的最高气温与最低气温记录如下表:
星期 一 二 三 四 五 六 日
最高气温 10℃ 12℃ 11℃ 9℃ 7℃ 5℃ 7℃
最低气温 2℃ 1℃ 0℃ -1℃ -4℃ -5℃ -5℃
则温差最大的一天是星期　　　　;温差最小的一天是星期　　　　.
【解析】计算得这七天的温差分别是:8℃ ( http: / / www.21cnjy.com ),11℃,11℃,10℃,11℃,10℃,12℃.所以温差最大的一天是星期日;温差最小的一天是星期一.
答案:日　一
5.以地面为基准,A处高+2.5m,B处高-17.8m,C处高-32.4m.问:
(1)A处比B处高多少
(2)B处和C处哪个地方高 高多少
(3)A处和C处哪个地方低 低多少
【解析】(1)(+2.5)-(-17.8)=2.5+17.8=20.3(m).
(2)B处高,(-17.8)-(-32.4)=-17.8+32.4=14.6(m),高14.6m.
(3)C处低,(+2.5)-(-32.4)=2.5+32.4=34.9(m),低34.9m.
【知识拓展】作差法比较大小
　　利用有理数减法可比较两个数的大小,即 ( http: / / www.21cnjy.com )如果要比较a与b的大小,先求a与b的差a-b.当a-b>0时,a>b;当a-b=0时,a=b;当a-b<0时,a【错在哪？】作业错例 课堂实拍
计算:-1-.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错: .
答案：(1)①
(2)
复习题训练及解析（九）
有理数的加减混合运算
1.下列交换加数的位置的变形中,正确的是　(　　)
A.1-4+5-4=1-4+4-5
B.-+--=+--
C.1-2+3-4=2-1+4-3
D.4.5-1.7-2.5+1.8=4.5-2.5+1.8-1.7
【解析】选D.1-4+5-4=1-4-4+5,故A项错误,-+--=-+--,故B项错误,1-2+3-4=-2+1-4+3,故C项错误,D项变形正确.
2.式子-6-8+10+6-5读作　　　　　　　　　　　　　　,或读作　　　　　　　　　　,计算结果为　　　　.
【解析】从性质和运算上读,
-6-8+10+6-5=-6-8-5+10+6
=-19+16=-3.
答案:负6、负8、正10、正6、负5的和　负6减8加10加6减5　-3
3.(2014·芜湖实验期中检测)把(+3)-(-6)-(+7)+(-8)写成省略加号的和的形式为　　　　　　.
【解析】(+3)-(-6)-(+7)+(-8)=(+3)+(+6)+(-7)+(-8)=3+6-7-8.
答案:3+6-7-8
4.计算(-0.25)-+2.75-=　　　　.
【解析】原式=-0.25+3.25+2.75-7.5=3+2.75-7.5
=5.75-7.5=-1.75.
答案:-1.75
【一题多解】本题还可以统一为加法后运用运算律
原式=(-0.25)+(+3.25)+2.75+(-7.5)
=(3.25+2.75)+(-0.25-7.5)=6+(-7.75)=-1.75.
答案:-1.75
5.已知有理数a,b,c在数轴上的位置如图所示,且|a|=1,|b|=2,|c|=4,则a-b+c=　　　　.
【解题指南】由数轴上各个点的位置→a,b,c的正负;
由|a|=1,|b|=2,|c|=4→a,b,c的值;
把a,b,c的值代入求值.
【解析】因为a,c在原点的左侧,b在原点的右侧,
所以b>0,c<0,a<0,
因为|a|=1,|b|=2,|c|=4,所以a=-1,b=2,c=-4,
所以a-b+c=-1-2-4=-7.
答案:-7
6.规定一种新运算:a△b=a-b+1,如3△4=3-4+1=0,那么2△(-3)的值是　　　　.
【解析】根据题意,因为a△b=a-b+1,
所以2△(-3)=2-(-3)+1=6.
答案:6
【互动探究】如果(-2)△x=-8,x的值是多少
【解析】-2-x+1=-8,x=-2+1+8,即x=7.
7.计算:
(1)(2014·南通实验质检)12-+-15.
(2)(2014·抚州实验期中)-20+(-14)-(-18)+13.
(3)(2014·陆丰东海中学期中)-20+(-6)+23-(-20).
【解析】(1)原式=12+18+[(-7)+(-15)]=30+(-22)=8.
(2)原式=[-20+(-14)]+(18+13)=-34+31=-3.
(3)原式=-20+(-6)+23+20=[(-20)+20]+[(-6)+23]=17.
有理数加减混合运算的实际应用
1.某天上午6:00柳江河水位为80.4m, ( http: / / www.21cnjy.com )到上午11:30水位上涨了5.3m,到下午6:00水位又跌了0.9m,下午6:00水位应为　(　　)
A.76 m B.84.8 m C.85.8 m D.86.6 m
【解析】选B.根据题意列算式得:80.4+5.3-0.9=85.7-0.9=84.8(m).
2.某小商店一周中每天的盈亏情况如表所示(盈利为“+”,亏损为“-”)
星期 一 二 三 四 五 六 日
盈亏的情况(元) +128.3 -25.6 +237.3 -7 -3 +322.5 +312.3
这一周的盈亏情况为　　　　　　　　.
【解析】因为128.3+(-25.6)+237.3+(-7)+(-3)+322.5+312.3
=(128.3+237.3+322.5+312.3)+[(-25.6)+(-7)+(-3)]
=1000.4+(-35.6)
=964.8(元).
所以这一周总的盈亏情况为盈利964.8元.
答案:盈利964.8元
3.张村共有10块小麦田,今年的收成与去年相比(增产为正,减产为负)的情况如下:
55kg,79 kg,-40 kg, ( http: / / www.21cnjy.com )-25 kg,10 kg,-16 kg,27 kg,-5 kg,31 kg,4 kg,今年的小麦总产量与去年相比情况如何
【解析】55+79+(-40)+(-25)+10+(-16)+27+(-5)+31+4
=(55+79+10+27+31+4)+[(-40)+(-16)+(-25)+(-5)]=206-86=120(kg).
答:今年的小麦总产量与去年相比增产120kg.
【知识归纳】有理数加减混合运算的实际应用的三点注意
1.根据有理数的意义,确定最多、最少.
2.计算各个数的和,确定增减总量.
3.增减总量+平均总量=实际总量.
4.某摩托车厂本周内计划每日生产300 ( http: / / www.21cnjy.com )辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如表(增加的车辆数为正数,减少的车辆数为负数)
星期 一 二 三 四 五 六 日
增减 -5 +7 -3 +4 +10 -9 -25
(1)本周三生产了多少辆摩托车
(2)本周总生产量与计划生产量相比,是增加还是减少
(3)产量最多的一天比产量最少的一天多生产了多少辆
【解析】(1)本周三生产的摩托车为:300-3=297辆.
(2)本周总生产量为(-5)+(+7)+(-3)+(+4)+(+10)+(-9)+(-25)=-21辆,所以本周总生产量与计划生产量相比减少21辆.
(3)产量最多的一天比产量最少的一天多生产了(+10)-(-25)=35(辆),即产量最多的一天比产量最少的一天多生产了35辆.
【错在哪？】作业错例 课堂实拍
　计算:--+.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错: .
答案：(1)①
(2) 原式=
复习题训练及解析（十）
两个有理数的乘法运算
1.如果两个数的积为0,那么　(　　)
A.两个数都是0 B.两个数是相反数
C.两个数都不是0 D.两个数中至少有一个为0
【解析】选D.根据任何数与零相乘都得零可知,两个数中至少有一个为0.
2.下列计算正确的是　(　　)
A.(-7)×(-6)=-42 　　　　B.(-3)×(+5)=15
C.(-2)×0=0 　　　 　D.-7×4=×4=-26
【解析】选C.A错误,结果应为42;
B错误,结果应为-15;D错误,结果应为-30.
3.两个负分数相乘,结果可能是　(　　)
A.0
B.负整数
C.正整数或正分数
D.负分数
【解析】选C.如果两个负分数能够完全约分,把分母全部约去,则结果是正整数;如果不能完全约分,则结果是正分数.
4.(2013·衡阳中考)计算(-4)×=　　　　.
【解题指南】
两个数符号 积的符号 积的绝对值 积
同号 同号得正 4×=2 2
【解析】(-4)×=+=2.
答案:2
5.计算:0×(-3)×5=　　　　.
【解题指南】三个有理数相乘,按从左到右的顺序,先计算前两个有理数的乘积,然后把所得的积与第三个有理数相乘.
【解析】0×(-3)×5=0×5=0.
答案:0
6.2×=　　　　.
【解析】2×=×=-3.
答案:-3
7.的相反数与绝对值分别为m和n,则mn=　　　　.
【解析】的相反数与绝对值分别为m和n,那么m和n分别是-,.则mn=×=-.
答案:-
有理数乘法法则的应用
1.(2014·蒙城模拟)与-8的积为1的数是　(　　)
A.-8 B.8 C. D.-
【解析】选D.由于积是1大于0,∴这两个数是同号,故是负数;然后把-8与-分别与-8相乘判断选择.
2.如果ab<0,那么下列判断正确的是　(　　)
A.a<0,b<0 B.a>0,b>0
C.a≥0,b≤0 D.a<0,b>0或a>0,b<0
【解析】选D.因为ab<0,所以a与b异号,所以a<0,b>0或a>0,b<0.
3.已知两数相乘大于0,两数相加小于0,则这两数的符号为　(　　)
A.同正 B.同负
C.一正一负 D.无法确定
【解析】选B.由积大于0,得两数同号;由和小于0,得两个数都是负数.
4.已知|a|=5,|b|=2,且a+b<0,则ab的值是　(　　)
A.10 B.-10 C.10或-10 D.-3或-7
【解析】选C.由|a|=5,|b|=2,得a=±5,b=±2;
由a+b<0,得a=-5.
当a=-5,b=2时,ab=-10;
当a=-5,b=-2时,ab=10.
【变式训练】若a=1,|b|=4,则ab的值为　　　　.
【解析】由|b|=4,得b=±4;
当a=1,b=4时,ab=4;
当a=1,b=-4时,ab=1×(-4)=-4.
答案:±4
【易错提醒】当已知某一因数的绝对值,求两个有理数的积时,要分类讨论,这个因数可能是正数,也可能是负数.
5.已知:×2=+2,×3=+3,×4=+4,…,如果×10=+10(a,b都是正整数),那么a+b的值是多少
【解析】本题属于规律探究型问题,是近年中考的热点题型,解答此类问题的关键是要对已知信息进行合理分析,找出其内在规律.对于本题由规律可知×10=+10,所以a=10,b=9,所以a+b=10+9=19.
6.在一个秘密俱乐部中,有一种特殊 ( http: / / www.21cnjy.com )的算账方式:a*b=3a-4b,聪明的小东通过计算2*(-4)发现了这一秘密,他是这样计算的:“2*(-4)=3×2-4×(-4)=22”,假如规定:a*b=2a-3b-1,那么请你求2*(-3)的值.
【解析】2*(-3)=2×2-3×(-3)-1
=4-(-9)-1=4+9-1=12.
【错在哪？】作业错例 课堂实拍
　计算:×(-25).
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错: .
答案：(1)②
(2) 由同号得正，得积的符号为正，故：原式=×25=101
复习题训练及解析（十一）
多个有理数相乘
1.计算(-0.125)×15×(-8)×=[(-0.125)×(-8)]×,这里运用了乘法的　(　　)
A.结合律 B.交换律
C.分配律 D.交换律和结合律
【解析】选D.在计算中-8与15交换了位置,运用了乘法交换律,而-0.125与-8,15与-结合在一起,运用了乘法结合律.
2.(2013·洞头六校期中)如果五个有理数相乘,积为负,那么其中正因数有
　(　　)
A.2个 B.3个
C.4个 D.2个或4个或0个
【解析】选D.五个有理数相乘积为负,则必有奇数个负因数,即1个或3个或5个,故正因数为4个或2个或0个.
【易错提醒】题目中求“正”因数的个数,易误认为求“负”因数的个数.
3.(2013·成都七中月考)在下列各式中:
①(-3)×4×2.3×(-5);
②3.5×(-20)×4.6×(-1)×(-6)×0;
③(-1.5)×(-2.4)×(-3)×(-9)×5.3;
④(-3)×(-4)×(-5)×(-7)×(-10),
以上的各式结果为负数的个数有　(　　)
A.1个 B.2个 C.3个 D.4个
【解题指南】积为负数要满足两个条件:①不含0因数;②负因数的个数是奇数个.
【解析】选A.①、③中有偶数个负因数,故积为正数;②中含有0因数,故积为0;④中含有5个负因数,故积为负数.
4.四个各不相等的整数a,b,c,d,它们的积a·b·c·d=9,那么a+b+c+d的值是　　　　.
【解题指南】由于abcd=9,且a,b,c,d是整数,所以把9分解成四个不相等的整数的积,从而可确定a,b,c,d的值,进而求其和.
【解析】∵9=1×(-1)×3×(-3),
∴a+b+c+d=1+(-1)+3+(-3)=0.
答案:0
5.计算:(15.9)×(-1998)×(1199)×(-2000)×0=　　　　.
【解析】因为算式中含0因数,所以积为0.
答案:0
6.计算:
(1)(-4)×5×(-0.25).
(2)××(-2).
(3)××0×(-26).
【解析】(1)(-4)×5×(-0.25)=4×5×0.25=5.
(2)××(-2)=-××2=-1.
(3)××0×(-26)=0.
有理数乘法的分配律
1.计算×12时,应该运用　(　　)
A.加法交换律 B.乘法分配律
C.乘法交换律 D.乘法结合律
【解析】选B.用12和括号内的各数分别相乘,然后再把所得积相加,这个计算过程应用了乘法分配律.
【变式训练】计算(-3)×,用分配律计算过程正确的是　(　　)
A.(-3)×4+(-3)×
B.(-3)×4-(-3)×
C.3×4-(-3)×
D.(-3)×4+3×
【解析】选A.(-3)×=(-3)×=(-3)×4+(-3)×.
2.算式×4可以化为　(　　)
A.-3×4-×4 B.-3×4+3
C.-3×4+×4 D.-3×3-3
【解析】选A.可以将-3转换为-3-的形式,再利用乘法分配律计算.
【变式训练】简便方法计算:7.97×(-8).
【解析】7.97×(-8)=(8-0.03)×(-8)
=-64+0.24=-63.76.
3.计算:99×(-5)=　　　　.
【解析】99×(-5)=×(-5)=100×(-5)+×(-5)=-500+=-499.
答案:-499
4.计算:×60.
【解析】原式=×60+×60-×60=45+35-70=10.
5.(2013·泰州姜堰二中月考)求值:
(1)×(-36).
(2)×-×-×.
【解析】(1)原式=×(-36)+×(-36)-×(-36)
=(-6)-20+21=-26+21=-5.
(2)原式=-×=.
【知识归纳】有理数乘法分配律的应用
1.直接利用a(b+c)计算,将先加减再乘的运算转化为先乘,再加减.
2.逆用:将算式中的相同因数提出后再乘.
如:ab+ac=a(b+c).
3.注意:解答实际问题时,要注意分清题目条件,符合哪一种,然后对应运算.
【错在哪？】作业错例 课堂实拍
　计算:-24×.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:原式 .
答案：(1) ①
(2) =
复习题训练及解析（十二）
求一个数的倒数
1.(2013·南昌中考)-3的倒数是　(　　)
A. B.- C.± D.0
【解析】选B.因为-3=-,所以-3的倒数为-.
2.(2013·荆门中考)-6的倒数是　(　　)
A.6 B.-6 C. D.-
【解析】选D.-6的倒数是1÷(-6)=1×=-.
3.(2013·北京中考)-的倒数是　(　　)
A. B. C.- D.-
【解析】选D.由倒数的概念知-的倒数是-.
【变式训练】-的倒数的绝对值为　　　　.
【解析】因为-的倒数是-,-=,所以-的倒数的绝对值是.
答案:
4.若一个数的相反数为-2.5,则这个数是　　　　,它的倒数是　　　　.
【解析】若一个数的相反数为-2.5,则这个数是2.5,因为2.5×0.4=1,所以2.5的倒数是0.4.
答案:2.5　0.4
5.求下列各数的倒数:
(1)-3.(2)-.(3)0.45.
【解析】(1)因为(-3)×=1,所以-3的倒数是-.
(2)因为×=1,所以-的倒数是-.
(3)因为0.45=,×=1,所以0.45的倒数是.
有理数的除法运算
1.计算6÷(-3)的结果为　(　　)
A.- B.-2 C.-3 D.-18
【解题指南】
判断 选择 符号 绝对值 商
整除 法则二 负 6÷3 -2
不整除
【解析】选B.6÷(-3)=-(6÷3)=-2.
2.(2013·南江中学月考)计算:-3÷÷的结果是　(　　)
A.-3 B.3 C.-12 D.12
【解析】选C.原式=-3×(-2)×(-2)=-12.
3.计算:÷9×的正确结果是　(　　)
A.- B. C.- D.
【解析】选D.原式=××=.
【易错提醒】当算式中仅有乘除运算时,应按从左到右的顺序计算.切不可乱用乘法交换律和结合律,如本题中,切不可先算9×.
4.(2013·泰州永安质检)如果a,b互为倒数,c,d互为相反数,且m=-1,则代数式2ab-(c+d)+m2=　　　　.
【解析】由题意得ab=1,c+d=0,
故原式=2×1-0+(-1)2=3.
答案:3
【互动探究】将题中条件m=-1改为m的绝对值为8,求ab++(-m)=　　　　.
【解析】由=8,得m=±8.
当m=8时,原式=1+0-8=-7;
当m=-8时,原式=1+0-(-8)=9.
答案:-7或9
5.(2013·辽师附中质检)计算:
13÷6+÷6+÷6.
【解析】原式=13×+×+×=×=(-30)×=-5.
分数的化简
1.下列化简正确的是　(　　)
A.=- B.=-2011
C.=-1 D.=-
【解析】选D.=,=0,
=-2×2=-4,=-.
2.化简下列分数:(1)=　　　　.(2)=　　　.
【解析】(1)原式=(-21)÷3=-7.
(2)原式===.
答案:(1)-7　(2)
3.化简下列分数:
(1).(2).(3).
【解析】(1)=26÷(-4)=-(26÷4)=-.
(2)=(-2)÷(-12)=2÷12=.
(3)=÷(-7)=×=-.
【错在哪？】作业错例 课堂实拍
　计算:÷(-3)×.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错: .
答案：(1)①
(2)
复习题训练及解析（十三）
有理数的乘方运算
1.(2013·黔东南中考)(-1)2的值是　(　　)
A.-1　　　　　 B. 1　　　　　 C.-2　　　　　D. 2
【解析】选B.(-1)2=12=1.
2.(2013·日照中考)计算-22+3的结果是　(　　)
A.7　 B.5　 C.-1　 D.-5
【解析】选C.-22+3=-4+3=-1.
3.(2013·黄冈中考)-(-3)2=　(　　)
A.-3　 B.3　 C.-9　 D.9
【解析】选C.因为(-3)2=9,所以-(-3)2=-9.
4.(2014·江苏台东第一阶段质检)若有理数a,b满足+(b-4)2=0,则a-b的值为　　　　.
【解析】因为≥0,(b-4)2≥0,
且+(b-4)2=0,
所以a+6=0,b-4=0,即a=-6,b=4.
所以a-b=-6-4=-10.
答案:-10
【知识归纳】平方的非负意义:对于任意有理数的平方不可能是负数,所以任意有理数的平方的值总是非负的,即a2≥0.多个非负数相加和为0,则它们各个部分都是0.如(x-2)2+(y-3)2=0,则x-2=0,y-3=0.绝对值也具有非负意义,即≥0.
5.计算:×=　　　　.
【解析】×=×
=×=-.
答案:-
6.计算:(1).(2)(-0.3)3.(3)-(-2)4.
(4)-(-2)5.
【解析】(1)==.
(2)(-0.3)3==-.
(3)-(-2)4=-24=-16.
(4)-(-2)5=-(-25)=-(-32)=32.
乘方的实际应用
1.某种细菌在培养过程中,每半小时分裂一次(由一个分裂成两个).经过3个小时,这种细菌由1个可分裂为　(　　)
A.8个 B.16个 C.32个 D.64个
【解析】选D.每半小时分裂一次,一个 ( http: / / www.21cnjy.com )变为两个,实际是21个.分裂第二次时,2个就变为了22个.那么经过3小时,就要分裂6次.即26=2×2×2×2×2×2=64(个).
2.你喜欢吃拉面吗 拉面馆的师傅,用一 ( http: / / www.21cnjy.com )根很粗的面条,把两头捏合在一起拉伸再捏合,再拉伸…反复几次,就把这根很粗的面条拉成了许多细的面条,这样捏合到第5次时可拉出细面条　(　　)
A.10根 B.20根 C.5根 D.32根
【解析】选D.由题意得,捏合到第5次时可拉出细面条25=32(根).
【变式训练】如图,一根细长的 ( http: / / www.21cnjy.com )绳子,沿中间对折,再沿对折后的中间对折,这样连续沿中间对折5次,用剪刀沿5次对折后的中间将绳子全部剪断,此时细绳被剪成　(　　)
A.17段 B.32段 C.33段 D.34段
【解析】选C.根据题意分析 ( http: / / www.21cnjy.com )可得:连续对折5次后,共25段即32段;故剪刀沿对折5次后的绳子的中间将绳子剪断,相当于绳子被截断32次,即此时绳子将被剪成32+1=33段.
3.(2013·贺州中考)2615个位上的数字是　(　　)
A.2　　 B.4　　 C.6　　 D.8
【解析】选D.列表:
n 1 2 3 4 5 6 7 8 9 10
2n 2 4 8 16 32 64 128 256 512 1 024
观察上表,可以发现2的幂的个位上的数字按照 ( http: / / www.21cnjy.com )2,4,8,6的顺序,循环出现,四次一循环.因为615÷4=153……3,所以2615的个位上的数字是8.
【互动探究】215的个位数字是多少
【解析】因为2的幂的个位上的数字按照2,4,8,6的顺序循环出现,四次一循环.15÷4=3……3,故215的个位数字是8.
4.如图是某手机专卖柜台摆放的一幅“手机图” ( http: / / www.21cnjy.com ),第一行有1部手机,第二行有2部手机,第三行有4部手机,第四行有8部手机……你是否发现手机的排列规律 猜猜看,第五行有　　　　部手机、第十行有　　　　部手机.(可用乘方形式表示)
( http: / / www.21cnjy.com )
【解析】由题意和图示可知:第二行有21=2部 ( http: / / www.21cnjy.com )手机,第三行有22=4部手机,第四行有23=8部手机,所以第五行有24部手机、第十行有29部手机.
答案:24　29
5.(2013·镇江中考)地 ( http: / / www.21cnjy.com )震中里氏震级每增加1级,释放的能量增大到原来的32倍,那么里氏　　　　级地震释放的能量是3级地震释放能量的324倍.
【解析】设3级地震释放能量为a, ( http: / / www.21cnjy.com )则由题意可得4级地震释放能量为32a,5级地震释放能量为32×32a=322a,6级地震释放能量为32×322a=323a,7级地震释放能量为32×323a=324a,因此,里氏7级地震释放的能量是3级地震释放能量的324倍.
答案:7
6.(2014·泰州永安质检)定义一种对正整数n的“F”运算:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为(其中k是使结果为奇数的正整数),并且运算重复进行.例如,取n=26,则26 13 44 11 →….若n=449,则第2013次“F”运算的结果是　　　　.
【解析】449×3+5=1352;=169;
169×3+5=512;=1;
1×3+5=8;=1,…,1,8循环出现,所以第2013次“F”运算的结果是8.
答案:8
【错在哪？】作业错例 课堂实拍
　计算:-×(-2)2.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误.
(2)纠错:
答案：(1)① (2)
复习题训练及解析（十四）
用科学记数法表示较大的数
1.2014年3月5日上午9时,第十二届全 ( http: / / www.21cnjy.com )国人民代表大会第二次会议在人民大会堂开幕,国务院总理李克强作政府工作报告,在报告中指出:中国经济运行稳中向好.国内生产总值达到56.9万亿元,比上年增长7.7%.那么56.9万亿用科学记数法可表示为　(　　)
A.5.69×1013 B.56.9×1012
C.0.569×1014 D.5.69×1012
【解析】选A.56.9万亿=56900000000000=5.69×1013.
2.(2013·呼和浩特中考)用激光测距仪测得两物体之间的距离为14000000米,将14000000用科学记数法表示为　(　　)
A.14×107　　 B.1.4×106
C.1.4×107　　　 D.0.14×108
【解题指南】
定a 整数数位 定n 科学记数法
1.4 8 8-1 1.4×107
【解析】选C.因为14000000的整数数位有8位,
所以a=1.4,n=8-1=7,即得1.4×107.
3.(2013·宜昌中考)中国航母辽宁 ( http: / / www.21cnjy.com )舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500t,这个数据用科学记数法表示为　(　　)
A.6.75×104t　　 B.67.5×103t　
C.0.675×105t　　　 D.6.75×10-4t
【解析】选A.67500是5位整数,在用科学记数法表示时,a=6.75,n=5-1=4,所以67500=6.75×104.
【方法技巧】确定指数n的两种方法
(1)n等于原数的整数位数减1.
(2)小数点向左移动了几位,n就等于几.
4.(2013·自贡中考)我国南海某海域探明可燃冰储量约有194亿立方米,194亿用科学记数法表示为　(　　)
A.1.94×1010 B.0.194×1010
C.19.4×109 D.1.94×109
【解析】选A.因为194亿可还原为19400000000,所以这个数是11位整数,所以194亿=1.94×1010.
【一题多解】选A.因为194=1.94×102,亿可表示为108,所以这个数可表示为1.94×1010.
【变式训练】(2013·邵阳中考) ( http: / / www.21cnjy.com )据邵阳市住房公积金管理会议透露,今年我市新增住房公积金11.2亿元,其中11.2亿元可用科学记数法表示为　(　　)
A.11.2×108元 B.1.12×109元　
C.0.112×1010元 D.112×107元
【解析】选B.11.2亿元=1120000000元=1.12×109元,故选B.
5.“余额宝”“雾霾”“公务员加 ( http: / / www.21cnjy.com )薪”热点话题位居第十二届全国人民代表大会第二次会议“前三甲”,“民有所呼、会有所应”如何体现 新的变化传递出了怎样的信号 据武汉大学互联网科学研究中心统计,从2014年3月3日零时至3月8日17时,两会相关微博讨论量为3162200条,两会相关新闻报道数为196000条.那么3162200用科学记数法可表示为　　　　　　　.
【解析】3162200=3.1622×106.
答案:3.1622×106
6.(2013·牡丹江中考)据2013 ( http: / / www.21cnjy.com )年黑龙江省垦区交通运输工作会议消息,今年垦区计划投资27亿元用于公路建设,将为全垦区社会经济发展提供有力支撑.27亿元用科学记数法表示为　　　　元.
【解析】27亿=2.7×109.
答案:2.7×109
7.(2013·莆田中考)小明同学 ( http: / / www.21cnjy.com )在“百度”搜索引擎中输入“中国梦”,搜索到相关的结果个数约为8650000,将这个数用科学记数法表示为　　　　　　　.
【解析】因为8650000的整数数位有7位,所以a=8.65,n=7-1=6.故8650000=8.65×106.
答案:8.65×106
8.用科学记数法表示下列各数:
(1)2130000.(2)-324.7.(3)32800.
【解析】(1)2130000=2.13×106.
(2)-324.7=-3.247×102.
(3)32800=3.28×104.
把用科学记数法表示的数化为原数
1.2013年某省国税系统完成税收收入约7.778×1011元,也就是该省2013年国税系统完成税收收入约为　(　　)
A.777.8亿元 B.7778亿元 C.77.78亿元 D.77780亿元
【解析】选B.7.778×1011=7.778×100000000000
=777800000000=7778亿.
2.一批货物总质量为1.2×107kg,下列运输工具可将其一次运走的是　(　　)
A.一艘万吨级巨轮 B.一辆汽车
C.一辆拖拉机 D.一辆马车
【解析】选A.1.2×107kg=12000000÷1000t=12000t,所以可将其一次运走的是一艘万吨级巨轮.
【变式训练】据统计,全球每分钟有8.5×106t污水排入江河湖海,也就是说排污量是　　　　万吨.
【解析】8.5×106=850×104,即850万吨.
答案:850
3.3.7895×103的整数位数有　　　　位.
【解析】3.7895×103化为原数为3789.5,所以整数位数有4位.
答案:4
4.国家体育场的“鸟巢”钢结构工程施 ( http: / / www.21cnjy.com )工建设中,首次使用了我国科研人员自主研制的强度为4.6×108Pa的钢材,那么4.6×108的原数为　　　　.
【解析】4.6×108=460000000.
答案:460000000
5.地球绕太阳的公转速度约1.1×108m/h,用科学记数法表示的原数为
　　　　m/h.
【解析】1.1×108=110000000.
答案:110000000
6.下列各数是用科学记数法表示的数,原来分别是什么数
(1)1×106.(2)3.14×103.
(3)-1.414×105.(4)1.732×107.
【解析】(1)1×106=1000000.(2)3.14×103=3140.
(3)-1.414×105=-141400.
(4)1.732×107=17320000.
【错在哪？】作业错例 课堂实拍
某市统计局发布2013年一季度全市完成GDP共317亿元,居全省第二位,将这一数据用科学记数法表示为　(　　)
A.31.7×109元　　　　　　
B.3.17×1010元
C.3.17×1011元
D.31.7×1010元
( http: / / www.21cnjy.com )
(1)错因:上面科学记数法表示中 错误.
(2)纠错:
答案：(1) a和n
(2)正确的表示是:3.17×1010,答案选B.
复习题训练及解析（十五）
有理数的混合运算
1.计算22×(-2)3+|3|的结果是　(　　)
A.-29　　　　　 B.-1　　　 　　C.0　　 　　　D.-2
【解析】选A.22×(-2)3+|3|=4×(-8)+3=-32+3=-29.
2.计算:25-3[32+2×(-3)]+5的结果是　(　　)
A.21 B.30 C.39 D.71
【解题指南】本题的计算顺序是:先算括号中的乘方和乘法,再去括号,最后算加减.
【解析】选A.25-3[32+2×(-3)]+5=25-3×[9-6]+5=21.
3.计算:(-2×5)3=　(　　)
A.1000 B.-1000 C.30 D.-30
【解析】选B.(-2×5)3=(-10)3=-1000.
【变式训练】计算:-2×32-(-2×32)=　(　　)
A.0 B.-54 C.-72 D.-18
【解析】选A.-2×32-(-2×32)=-2×9-(-2×9)=-18-(-18)=-18+18=0.
4.(2014·资阳实验质检)规定△是 ( http: / / www.21cnjy.com )一种新的运算符号,且a△b=a2-a×b+a-1,例如:计算2△3=22-2×3+2-1=4-6+2-1=-1.请你根据上面的规定试求4△5的值.
【解析】4△5=42-4×5+4-1=16-20+4-1=-1.
5.(2013·成都七中月考)计算:
-52-÷.
【解析】原式=-25-[-8+(1-0.6)]÷=-25-[-8+(1-0.6)]÷2=-25-(-7.6)÷2=-25+3.8=-21.2.
6.计算:(1)×+÷.
(2)-12-×[2-(-2)2].
【解析】(1)×+÷
=-×+×
=-+=.
(2)-12-×[2-(-2)2]
=-1-×(2-4)
=-1-×(-2)
=-1+=-.
【知识归纳】有理数混合运算的运算级别
　　加减运算是第一级运算,乘除运算是第二级运算,乘方运算是第三级运算.
①运算顺序:要先算第三级运算,再算第二级运算,最后算第一级运算;
②同一级的运算按从左到右的先后顺序进行;
③有括号时,先算小括号里面的,再算中括号里面的,最后算大括号里面的.
有理数混合运算中的运算律的应用
1.算式5×52-4×52运用下列哪种运算律运算较简便　(　　)
A.乘法交换律 B.乘法结合律
C.加法结合律 D.乘法分配律
【解析】选D.逆用乘法分配律可使运算简便.
5×52-4×52=52×(5-4)
=52×1=25×1=25.
2.-24÷×等于　(　　)
A.-16 B.-81
C.16 D.81
【解析】选B.原式=-16××=-81.
3.计算:1×-×2+×=　　　　　.
【解析】1×-×2+×
=×
=×
=.
答案:
4.计算:(-5)×+(-7)×+12×.
【解析】(-5)×+(-7)×+12×
=×[(-5)+(-7)+12]
=×(-5-7+12)
=×(-12+12)=×0=0.
【变式训练】计算:÷.
【解析】原式=×(-64)
=×(-64)-×(-64)+×(-64)-×(-64)
=-32+16-24+4
=-32-24+16+4
=-56+20=-36.
5.(2014·沈丘外语中学质检)计算:÷.
【解析】原式=×(-4)
=×(-4)
=2×(-4)-×(-4)=-3.
6.(2014·无锡南菁中学质检)计算:
-14-×6.
【解析】原式=-1-
=-1-=-1-(6-5)=-2.
【错在哪？】作业错例 课堂实拍
　计算:-22÷×-×23.
( http: / / www.21cnjy.com )
(1)找错:从第 步开始出现错误,出错原因是 错.
(2)纠错:
答案：(1)① 运算顺序 (2) 原式=-4×××8=--4=-.