第五单元《平行四边形的面积(1)》(教案)五年级上册数学沪教版
文档属性
| 名称 | 第五单元《平行四边形的面积(1)》(教案)五年级上册数学沪教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 339.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 12:05:43 | ||
图片预览

文档简介
平行四边形的面积(1)
教学内容:
沪教版小学数学第九册P64-65
教学目标:
1.利用割补.拼摆等方法,探索并掌握平行四边形的面积计算公式。会计算平行四边形的面积。
2.初步学会利用平行四边形的面积公式求有关数据。
3.经历动手操作.探索.发现的过程,并在此过程中体验成功的喜悦。
教学重点:
掌握平行四边形的面积计算公式。
教学难点:
理解平行四边形的面积计算公式的推导过程。
教具准备:
平行四边形磁铁棒.2个平行四边形(2组底边用2种颜色描好).剪刀.水彩笔
教学过程:
一、故事引入(借鉴一师一优课)
师:向阳小学要建成一个花园学校,他们决定由各个班级来承包几块地,种植绿化,并进行评比。以下是五年级三个班级承包的地,它们的面积分别是多少?
出示: 五(1)班 五(2)班 五(3)班
生:五(1)班:5×2=10(平方米)
五(2)班:3×3=9(平方米)
师:长方形和正方形的面积我们都学过,公式分别是:
长方形的面积=长×宽 正方形的面积=边长×边长
S=a×b S=a
师:那五(3)班承包的地是一个平行四边形,它的面积该怎么求呢?
今天我们就要来研究“平行四边形的面积”。(板书课题)
二、探究过程
(一)用数方格的方法数出平行四边形的面积:(借鉴空中课堂)
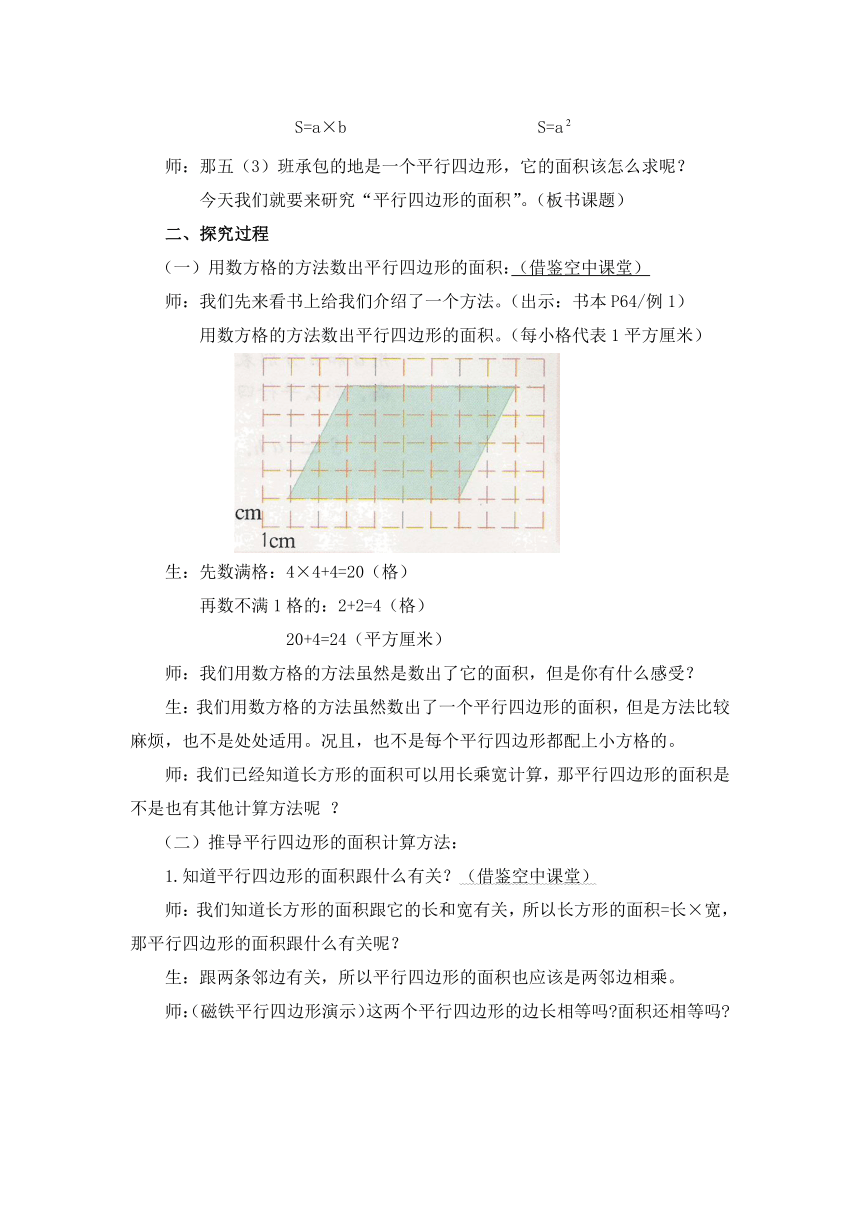
师:我们先来看书上给我们介绍了一个方法。(出示:书本P64/例1)
用数方格的方法数出平行四边形的面积。(每小格代表1平方厘米)
生:先数满格:4×4+4=20(格)
再数不满1格的:2+2=4(格)
20+4=24(平方厘米)
师:我们用数方格的方法虽然是数出了它的面积,但是你有什么感受?
生:我们用数方格的方法虽然数出了一个平行四边形的面积,但是方法比较麻烦,也不是处处适用。况且,也不是每个平行四边形都配上小方格的。
师:我们已经知道长方形的面积可以用长乘宽计算,那平行四边形的面积是不是也有其他计算方法呢 ?
(二)推导平行四边形的面积计算方法:
1.知道平行四边形的面积跟什么有关?(借鉴空中课堂)
师:我们知道长方形的面积跟它的长和宽有关,所以长方形的面积=长×宽,那平行四边形的面积跟什么有关呢?
生:跟两条邻边有关,所以平行四边形的面积也应该是两邻边相乘。
师:(磁铁平行四边形演示)这两个平行四边形的边长相等吗 面积还相等吗
说明什么
生:平行四边形的面积跟邻边没有关系。
师:那跟什么有关?
生:跟它的底和高有关。
师:原来平行四边形在变动时,周长不变,但面积在变化。同样以这条边为底,高越高,面积就越大;高越低,面积就越小。
2.推导平行四边形的面积公式:(播放空中课堂)
师:那平行四边形的面积跟它的底和高存在什么关系呢?你能利用手中的工具,想办法证明平行四边形的面积计算方法吗?
生:先各自动手尝试,再组内交流,并反馈。
把平行四边形剪一刀,拼成一个长方形,……
(学生操作后)提问
师:①你是沿着哪条线把平行四边形剪开的 (高)
②剪开后,你是怎样拼成长方形的 (边回答边演示)
师:平行四边形转化成长方形后,什么变了 什么没变
(形状变了,面积没变)
师:长方形的长与平行四边形的底有什么关系 长方形的宽与平行四边形的高有什么关系 根据这些条件,你能推导出平行四边形的面积计算公式吗 (形成完整的板书)
长方形的面积 = 长 × 宽
‖ ‖ ‖
平行四边形面积 = 底 × 高
师:刚才我们是沿着这条高剪开的,如果沿着另一条高剪开,是不是得到同样的结论呢?我们再来演示一下。(师沿着另一条高剪开演示)
得到的结论一样吗?
生:一样。
师:我们也可以用字母来表示。
板书:S=ah
师:但是,大家必须注意,底×高,必须乘的是底所对应的高。
如:(标上高3m)
4m
S=ah
=4×3
=12(平方米)
答:这个平行四边形的面积是12平方米。
师:也可以告诉你另一组底和相对应的高。(标上高5m)
2.4m
S=ah
=2.4×5
=12(平方米)
答:这个平行四边形的面积是12平方米。
师:底×高,一定是相对应的高,不能去找别人的高,否则就错了。
三.巩固练习:
1.书本P65/试一试/1
2.解决问题:
(1)有一块平行四边形的铁皮,底是8.5厘米,高是7.2厘米,面积是多少平方厘米?
(2)一块平行四边形的土地,底是27米,是高的3倍。这块地的面积是多少平方米?
(3)书本P65/试一试3:
四、总结
今天你有什么收获?
五、板书设计
平行四边形的面积(1)
长方形的面积 = 长 × 宽
‖ ‖ ‖
平行四边形面积 = 底 × 高
S=ah
S=ah S=ah
=4×3 =2.4×5
=12(平方米) =12(平方米)
答:这个平行四边形的 答:这个平行四边形的
面积是12平方米。 面积是12平方米。
教学内容:
沪教版小学数学第九册P64-65
教学目标:
1.利用割补.拼摆等方法,探索并掌握平行四边形的面积计算公式。会计算平行四边形的面积。
2.初步学会利用平行四边形的面积公式求有关数据。
3.经历动手操作.探索.发现的过程,并在此过程中体验成功的喜悦。
教学重点:
掌握平行四边形的面积计算公式。
教学难点:
理解平行四边形的面积计算公式的推导过程。
教具准备:
平行四边形磁铁棒.2个平行四边形(2组底边用2种颜色描好).剪刀.水彩笔
教学过程:
一、故事引入(借鉴一师一优课)
师:向阳小学要建成一个花园学校,他们决定由各个班级来承包几块地,种植绿化,并进行评比。以下是五年级三个班级承包的地,它们的面积分别是多少?
出示: 五(1)班 五(2)班 五(3)班
生:五(1)班:5×2=10(平方米)
五(2)班:3×3=9(平方米)
师:长方形和正方形的面积我们都学过,公式分别是:
长方形的面积=长×宽 正方形的面积=边长×边长
S=a×b S=a
师:那五(3)班承包的地是一个平行四边形,它的面积该怎么求呢?
今天我们就要来研究“平行四边形的面积”。(板书课题)
二、探究过程
(一)用数方格的方法数出平行四边形的面积:(借鉴空中课堂)
师:我们先来看书上给我们介绍了一个方法。(出示:书本P64/例1)
用数方格的方法数出平行四边形的面积。(每小格代表1平方厘米)
生:先数满格:4×4+4=20(格)
再数不满1格的:2+2=4(格)
20+4=24(平方厘米)
师:我们用数方格的方法虽然是数出了它的面积,但是你有什么感受?
生:我们用数方格的方法虽然数出了一个平行四边形的面积,但是方法比较麻烦,也不是处处适用。况且,也不是每个平行四边形都配上小方格的。
师:我们已经知道长方形的面积可以用长乘宽计算,那平行四边形的面积是不是也有其他计算方法呢 ?
(二)推导平行四边形的面积计算方法:
1.知道平行四边形的面积跟什么有关?(借鉴空中课堂)
师:我们知道长方形的面积跟它的长和宽有关,所以长方形的面积=长×宽,那平行四边形的面积跟什么有关呢?
生:跟两条邻边有关,所以平行四边形的面积也应该是两邻边相乘。
师:(磁铁平行四边形演示)这两个平行四边形的边长相等吗 面积还相等吗
说明什么
生:平行四边形的面积跟邻边没有关系。
师:那跟什么有关?
生:跟它的底和高有关。
师:原来平行四边形在变动时,周长不变,但面积在变化。同样以这条边为底,高越高,面积就越大;高越低,面积就越小。
2.推导平行四边形的面积公式:(播放空中课堂)
师:那平行四边形的面积跟它的底和高存在什么关系呢?你能利用手中的工具,想办法证明平行四边形的面积计算方法吗?
生:先各自动手尝试,再组内交流,并反馈。
把平行四边形剪一刀,拼成一个长方形,……
(学生操作后)提问
师:①你是沿着哪条线把平行四边形剪开的 (高)
②剪开后,你是怎样拼成长方形的 (边回答边演示)
师:平行四边形转化成长方形后,什么变了 什么没变
(形状变了,面积没变)
师:长方形的长与平行四边形的底有什么关系 长方形的宽与平行四边形的高有什么关系 根据这些条件,你能推导出平行四边形的面积计算公式吗 (形成完整的板书)
长方形的面积 = 长 × 宽
‖ ‖ ‖
平行四边形面积 = 底 × 高
师:刚才我们是沿着这条高剪开的,如果沿着另一条高剪开,是不是得到同样的结论呢?我们再来演示一下。(师沿着另一条高剪开演示)
得到的结论一样吗?
生:一样。
师:我们也可以用字母来表示。
板书:S=ah
师:但是,大家必须注意,底×高,必须乘的是底所对应的高。
如:(标上高3m)
4m
S=ah
=4×3
=12(平方米)
答:这个平行四边形的面积是12平方米。
师:也可以告诉你另一组底和相对应的高。(标上高5m)
2.4m
S=ah
=2.4×5
=12(平方米)
答:这个平行四边形的面积是12平方米。
师:底×高,一定是相对应的高,不能去找别人的高,否则就错了。
三.巩固练习:
1.书本P65/试一试/1
2.解决问题:
(1)有一块平行四边形的铁皮,底是8.5厘米,高是7.2厘米,面积是多少平方厘米?
(2)一块平行四边形的土地,底是27米,是高的3倍。这块地的面积是多少平方米?
(3)书本P65/试一试3:
四、总结
今天你有什么收获?
五、板书设计
平行四边形的面积(1)
长方形的面积 = 长 × 宽
‖ ‖ ‖
平行四边形面积 = 底 × 高
S=ah
S=ah S=ah
=4×3 =2.4×5
=12(平方米) =12(平方米)
答:这个平行四边形的 答:这个平行四边形的
面积是12平方米。 面积是12平方米。
同课章节目录
