1.1第三课时 菱形的性质与判定的综合应用 课件(共22张PPT) 2023-2024学年度北师大版数学九年级上册
文档属性
| 名称 | 1.1第三课时 菱形的性质与判定的综合应用 课件(共22张PPT) 2023-2024学年度北师大版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 18:33:27 | ||
图片预览





文档简介
(共22张PPT)
第一章 特殊平行四边形
第3课时 菱形的性质与判定的综合
1 菱形的性质与判定
学习目标
学习目标
1.能灵活运用菱形的性质定理及判定定理解决一些相关问题,并掌握菱形面积的求法。
2.经历菱形性质定理及判定定理的应用过程,体会数形结合、转化等思想方法。
新课导入
壹
新课导入
1.菱形是 图形也是 图形.
2.菱形的四条边都 .
3.菱形的两条对角线互相 .
轴对称
中心对称
相等
垂直且平分
温故知新
4. 菱形的判定:
(1)_________________________________
(2)_________________________________
(3)_________________________________
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边相等的四边形是菱形
讲授新知
贰
讲授新课
平行四边形的面积=_________.
F
底×高
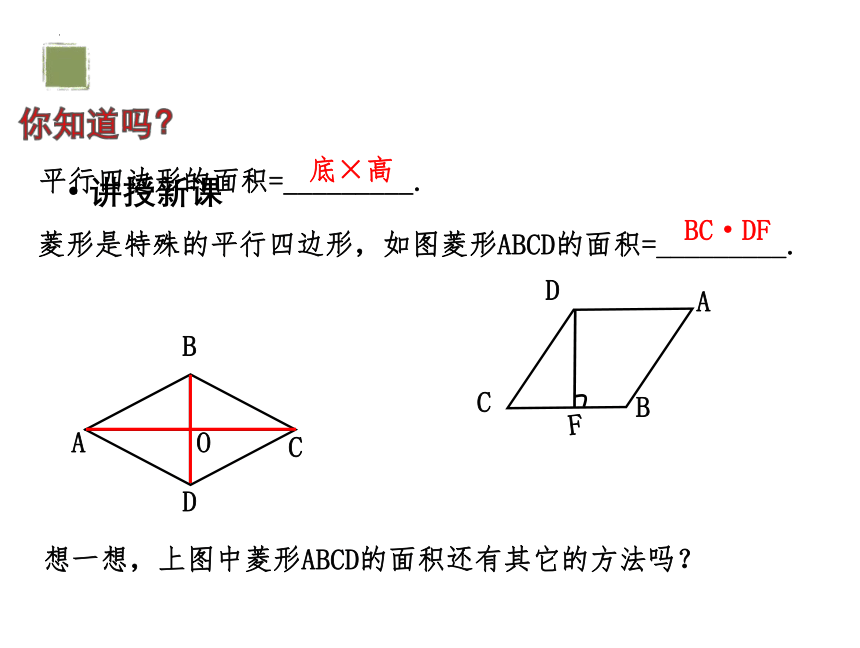
菱形是特殊的平行四边形,如图菱形ABCD的面积=_________.
BC·DF
想一想,上图中菱形ABCD的面积还有其它的方法吗?
A
B
C
O
D
B
A
C
D
你知道吗?
讲授新课
A
B
C
D
O
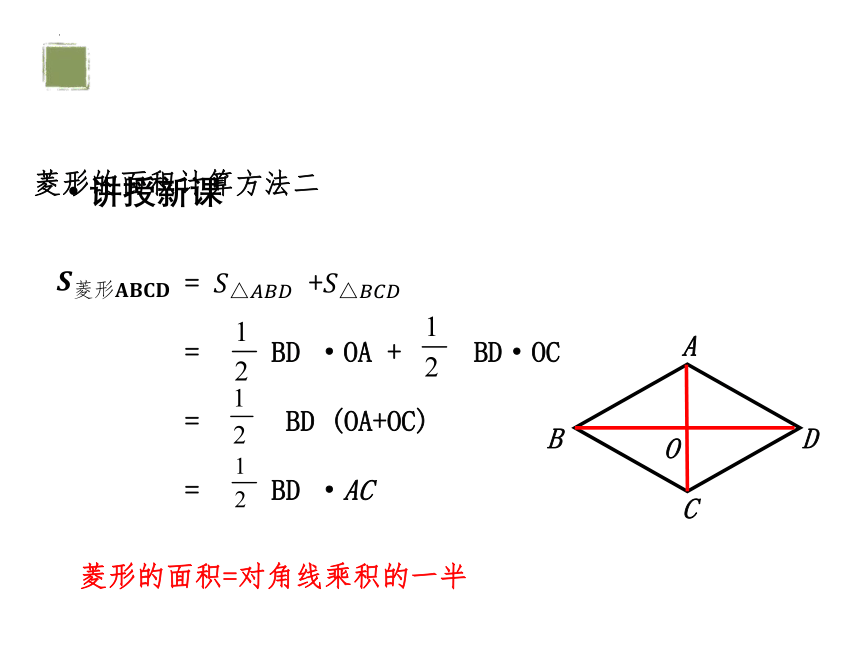
菱形的面积计算方法二
= +
= BD ·OA + BD·OC
= BD (OA+OC)
= BD ·AC
菱形的面积=对角线乘积的一半
讲授新课
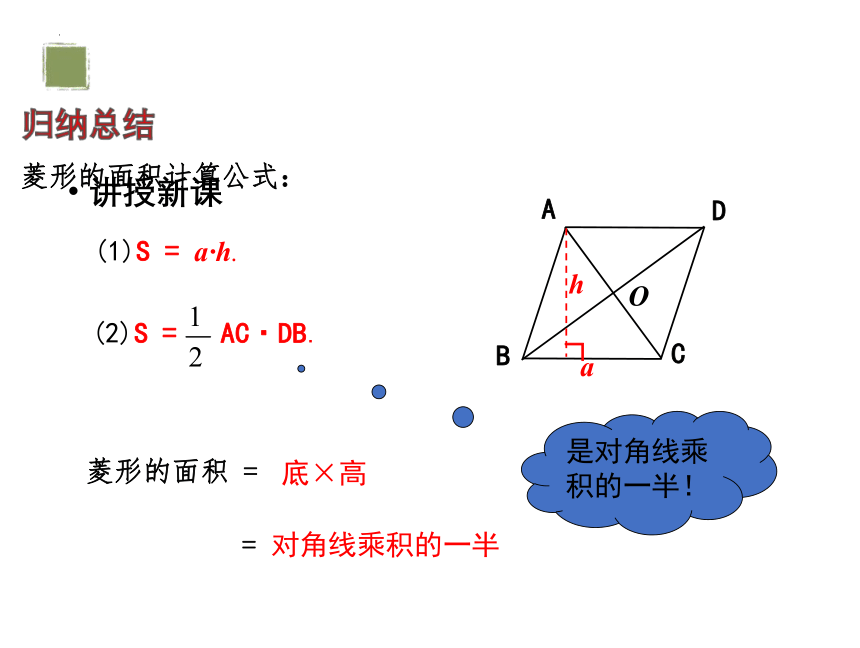
(1)S = a·h.
菱形的面积计算公式:
菱形的面积 =
O
= 对角线乘积的一半
(2)S = AC·DB.
A
B
C
D
a
∟
h
底×高
归纳总结
是对角线乘积的一半!
范例应用
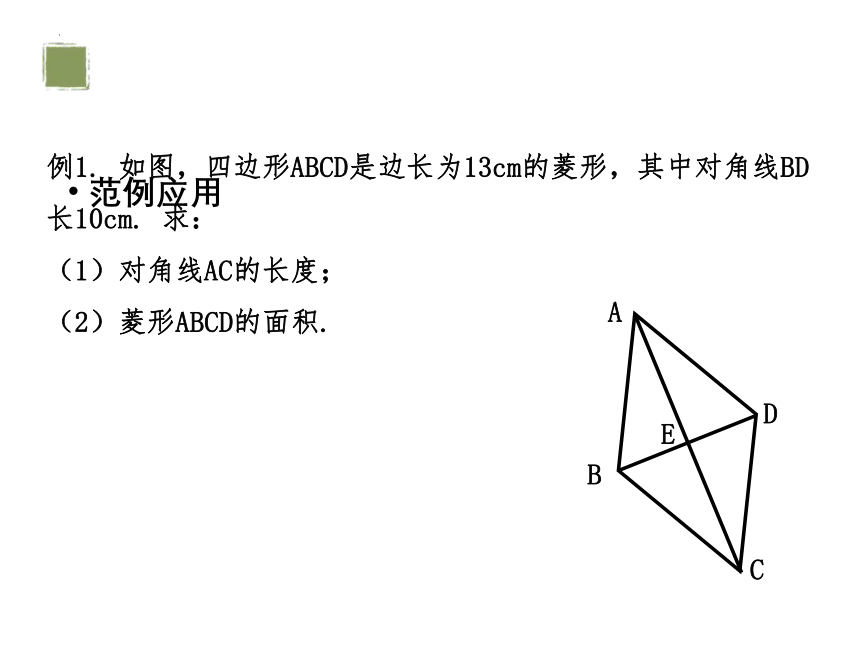
例1. 如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm. 求:
(1)对角线AC的长度;
(2)菱形ABCD的面积.
A
B
C
D
E
范例应用
解:(1)∵四边形ABCD是菱形,AC与BD相交于点E
∴∠AED=90°
DE= BD = ×10 = 5 (cm)
在Rt △ADE中,由勾股定理,得
∴AC=2AE=2×12=24 (cm)
(2)S菱形ABCD= BD ×AC
= ×10×24= 120(cm2).
A
B
C
D
E
你知道为什么吗?
范例应用
例2 如图所示,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,AB=13,OA=5,OB=12.求菱形ABCD两对边的距离h.
解析:先利用菱形的面积等于两条对角线长度乘积的一半求得菱形的面积,又因为菱形是特殊的平行四边形,其面积等于底乘高,也就是一边长与两边之间距离的乘积,从而求得两对边的距离.
范例应用
解:在Rt△AOB中,AB=13,OA=5,OB=12,
于是
所以,S菱形ABCD=4S△AOB=4×30=120.
又因为菱形两组对边的距离相等,
所以,S菱形ABCD=AB h=13h,
即,13h=120,得
方法总结:菱形的面积计算有如下方法:
(1)一边长与两对边的距离(即菱形的高)的积;
(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍);
(3)两条对角线长度乘积的一半.
范例应用
做一做
如图两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是什么图形?为什么?
A
B
C
D
分析:画辅助线构建三角形,通过证明三角形全等得出相等的线段。
ABCD是菱形
当堂训练
叁
当堂训练
1.若菱形的两条对角线长分别为8和6 ,则这个菱形的面积是( )
A. 96 B. 48 C. 24 D. 12
A
B
C
D
C
2.如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
A. 2.4cm B. 4.8cm C. 5cm D. 9.6cm
B
当堂训练
3.如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=4cm,BD=8cm,则这个菱形的面积是 cm .
16
4.如图,菱形ABCD中,∠B=60°,点E在AB边上,点F在AD边上,BE=AF。若∠ECF=60°,△CEF为_______三角形。
等边
当堂训练
5.如图所示,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
又∵EF=BE,
∴四边形BCFE是菱形;
当堂训练
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .
方法总结:判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以尝试证出这个四边形是平行四边形,然后用定义法或判定定理1来证明菱形.
课堂小结
肆
课堂小结
菱形的性质与判定的综合性问题
菱形的周长面积
有关计算
周长=4×边长
面积=底×高=两条对角线乘积的一半
课后作业
基础题:1.课后习题 第 1,2,3,4题。
提高题:2.请学有余力的同学完成课后习题第5题。
谢
谢
第一章 特殊平行四边形
第3课时 菱形的性质与判定的综合
1 菱形的性质与判定
学习目标
学习目标
1.能灵活运用菱形的性质定理及判定定理解决一些相关问题,并掌握菱形面积的求法。
2.经历菱形性质定理及判定定理的应用过程,体会数形结合、转化等思想方法。
新课导入
壹
新课导入
1.菱形是 图形也是 图形.
2.菱形的四条边都 .
3.菱形的两条对角线互相 .
轴对称
中心对称
相等
垂直且平分
温故知新
4. 菱形的判定:
(1)_________________________________
(2)_________________________________
(3)_________________________________
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边相等的四边形是菱形
讲授新知
贰
讲授新课
平行四边形的面积=_________.
F
底×高
菱形是特殊的平行四边形,如图菱形ABCD的面积=_________.
BC·DF
想一想,上图中菱形ABCD的面积还有其它的方法吗?
A
B
C
O
D
B
A
C
D
你知道吗?
讲授新课
A
B
C
D
O
菱形的面积计算方法二
= +
= BD ·OA + BD·OC
= BD (OA+OC)
= BD ·AC
菱形的面积=对角线乘积的一半
讲授新课
(1)S = a·h.
菱形的面积计算公式:
菱形的面积 =
O
= 对角线乘积的一半
(2)S = AC·DB.
A
B
C
D
a
∟
h
底×高
归纳总结
是对角线乘积的一半!
范例应用
例1. 如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm. 求:
(1)对角线AC的长度;
(2)菱形ABCD的面积.
A
B
C
D
E
范例应用
解:(1)∵四边形ABCD是菱形,AC与BD相交于点E
∴∠AED=90°
DE= BD = ×10 = 5 (cm)
在Rt △ADE中,由勾股定理,得
∴AC=2AE=2×12=24 (cm)
(2)S菱形ABCD= BD ×AC
= ×10×24= 120(cm2).
A
B
C
D
E
你知道为什么吗?
范例应用
例2 如图所示,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,AB=13,OA=5,OB=12.求菱形ABCD两对边的距离h.
解析:先利用菱形的面积等于两条对角线长度乘积的一半求得菱形的面积,又因为菱形是特殊的平行四边形,其面积等于底乘高,也就是一边长与两边之间距离的乘积,从而求得两对边的距离.
范例应用
解:在Rt△AOB中,AB=13,OA=5,OB=12,
于是
所以,S菱形ABCD=4S△AOB=4×30=120.
又因为菱形两组对边的距离相等,
所以,S菱形ABCD=AB h=13h,
即,13h=120,得
方法总结:菱形的面积计算有如下方法:
(1)一边长与两对边的距离(即菱形的高)的积;
(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍);
(3)两条对角线长度乘积的一半.
范例应用
做一做
如图两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是什么图形?为什么?
A
B
C
D
分析:画辅助线构建三角形,通过证明三角形全等得出相等的线段。
ABCD是菱形
当堂训练
叁
当堂训练
1.若菱形的两条对角线长分别为8和6 ,则这个菱形的面积是( )
A. 96 B. 48 C. 24 D. 12
A
B
C
D
C
2.如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
A. 2.4cm B. 4.8cm C. 5cm D. 9.6cm
B
当堂训练
3.如图,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=4cm,BD=8cm,则这个菱形的面积是 cm .
16
4.如图,菱形ABCD中,∠B=60°,点E在AB边上,点F在AD边上,BE=AF。若∠ECF=60°,△CEF为_______三角形。
等边
当堂训练
5.如图所示,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
又∵EF=BE,
∴四边形BCFE是菱形;
当堂训练
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .
方法总结:判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以尝试证出这个四边形是平行四边形,然后用定义法或判定定理1来证明菱形.
课堂小结
肆
课堂小结
菱形的性质与判定的综合性问题
菱形的周长面积
有关计算
周长=4×边长
面积=底×高=两条对角线乘积的一半
课后作业
基础题:1.课后习题 第 1,2,3,4题。
提高题:2.请学有余力的同学完成课后习题第5题。
谢
谢
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
