28.九年级数学(下)第26章 反比例函数单元检测题(含答案)
文档属性
| 名称 | 28.九年级数学(下)第26章 反比例函数单元检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 349.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 19:44:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
28.九年级数学(下)第26章《反比例函数》单元检测题(月考一)
(测试范围:第26章全章内容 考试时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.如图某一反比例函数的图象,它的函数解析式可能是( )
A.y= B.y=x2 C.y=2x D.y=-
2.已知反比例函数y=的图象经过(1,-4),则k的值是( )
A.-4 B.4 C.2 D.-2
3.若反比例函数的图象经过点(-2,3),则该反比例函数图象一定经过点( )
A.(2,3) B.(2,-3) C.(-2,-3) D.(-1,-6)
4.已知甲、乙两地相距s(km),汽车从甲地行驶到乙地,则汽车行驶的时间t(h)与行驶速度(km/h)的函数关系图象大致是( )
A B C D
5.如图,A是反比例函数y=的图象上的一点,AB⊥x轴于点B,且△ABO的面积是2,则k的值是( )
A.2 B.-2 C.-4 D.4
6.正比例函数y=6x的图象与反比例函数y=的图象的交点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第一、三象限
7.已知反比例函数y=-,下列结论中正确的是( )
A.图象经过点(-1,-1) B.图象在第一、三象限
C.当x>0时,0<y<1 D.当x<0时,y随x的增大而增大
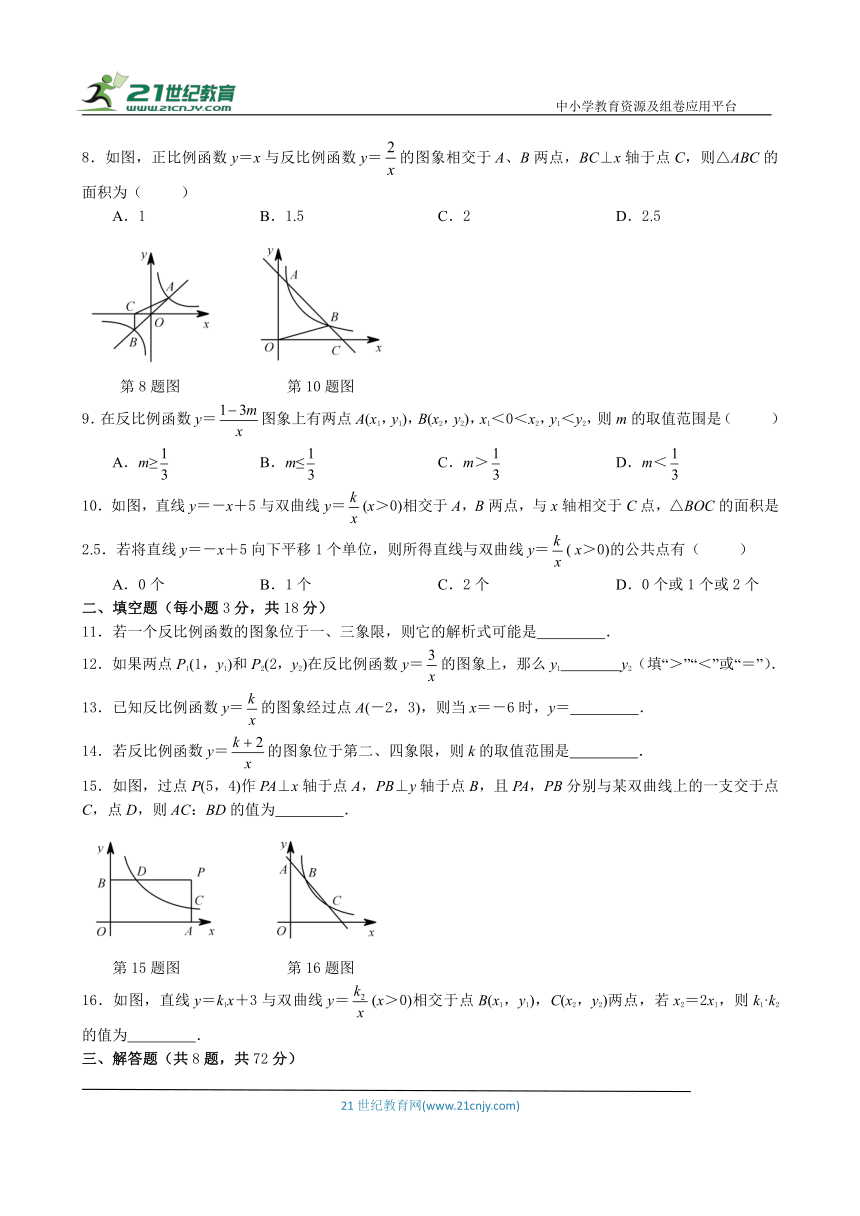
8.如图,正比例函数y=x与反比例函数y=的图象相交于A、B两点,BC⊥x轴于点C,则△ABC的面积为( )
A.1 B.1.5 C.2 D.2.5
第8题图 第10题图
9.在反比例函数y=图象上有两点A(x1,y1),B(x2,y2),x1<0<x2,y1<y2,则m的取值范围是( )
A.m≥ B.m≤ C.m> D.m<
10.如图,直线y=-x+5与双曲线y=(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是2.5.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=( x>0)的公共点有( )
A.0个 B.1个 C.2个 D.0个或1个或2个
二、填空题(每小题3分,共18分)
11.若一个反比例函数的图象位于一、三象限,则它的解析式可能是 .
12.如果两点P1(1,y1)和P2(2,y2)在反比例函数y=的图象上,那么y1 y2(填“>”“<”或“=”).
13.已知反比例函数y=的图象经过点A(-2,3),则当x=-6时,y= .
14.若反比例函数y=的图象位于第二、四象限,则k的取值范围是 .
15.如图,过点P(5,4)作PA⊥x轴于点A,PB⊥y轴于点B,且PA,PB分别与某双曲线上的一支交于点C,点D,则AC:BD的值为 .
第15题图 第16题图
16.如图,直线y=k1x+3与双曲线y=(x>0)相交于点B(x1,y1),C(x2,y2)两点,若x2=2x1,则k1·k2的值为 .
三、解答题(共8题,共72分)
17.(本题8分)反比例函数y=的图象经过点A(3,4).
(1)求k值;
(2)请判断点B(2,6)是否在这个反比例函数的图象上,并说明理由.
18.(本题8分)如图,已知一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3)和B(-3,m)两点.
(1)求这两个函数的解析式;
(2)直接写出△AOB的面积 .
19.(本题8分)如图,直线y=mx与双曲线y=相交于A,B两点,A点的坐标为(2,4).
(1)求反比例函数的解析式;
(2)直接写出线段AB的长是 .
20.(本题8分)已知直线y=-3x与双曲线y=交于点P(-1,n).
(1)求n,m的值;
(2)若点A(-3,y1),B(-1,y2)在双曲线y=上,比较y1,y2的大小.
21.(本题8分)如图,直线y=2x与双曲线y=在第一象限内交于点A(m,2),将直线y=2x向下平移后与反比例函数y=在第一象限内的图象交于点P,且△POA的面积为2.
(1)则k的值是 ;
(2)求平移后的直线的解析式.
22.(本题10分)如图,点B(3,3)在双曲线y=(x>0)上,点D在双曲线y=-(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(1)求k的值;
(2)求点A的坐标.
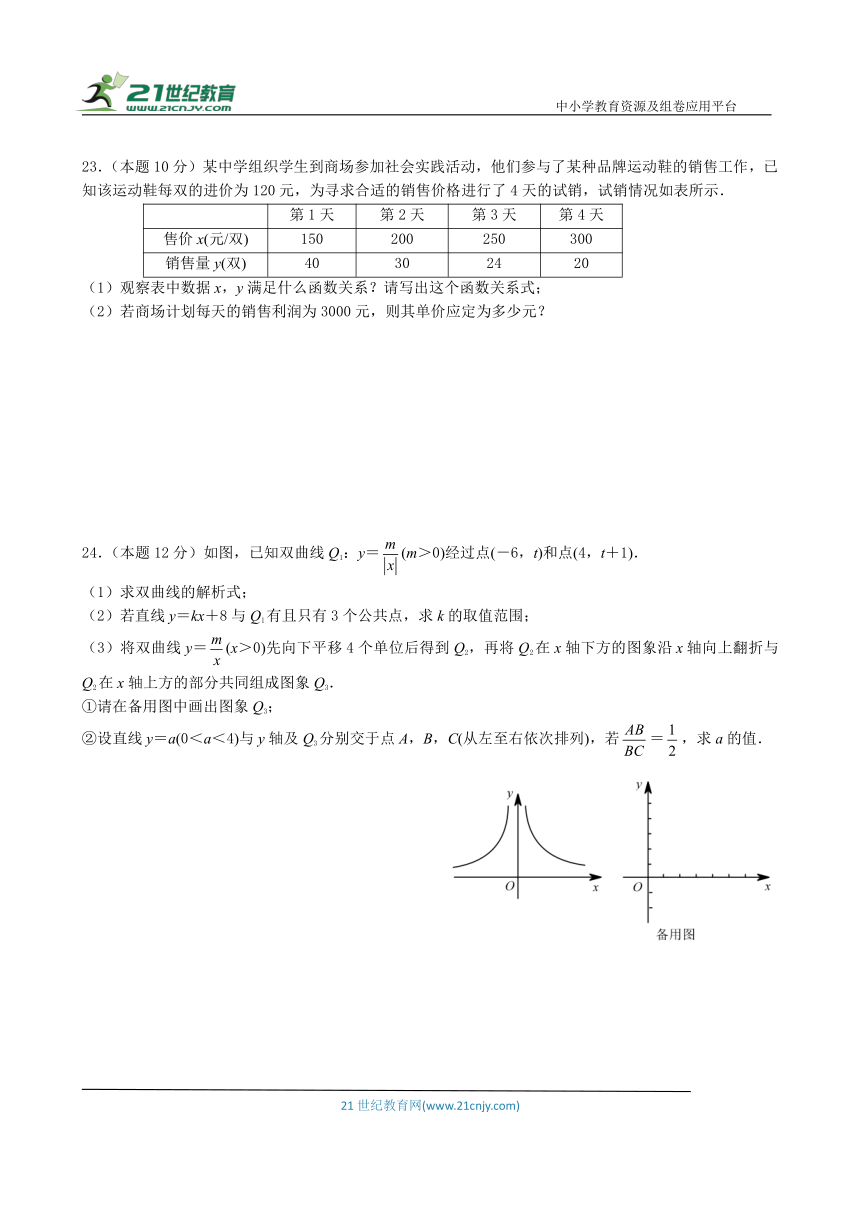
23.(本题10分)某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示.
第1天 第2天 第3天 第4天
售价x(元/双) 150 200 250 300
销售量y(双) 40 30 24 20
(1)观察表中数据x,y满足什么函数关系?请写出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
24.(本题12分)如图,已知双曲线Q1:y=(m>0)经过点(-6,t)和点(4,t+1).
(1)求双曲线的解析式;
(2)若直线y=kx+8与Q1有且只有3个公共点,求k的取值范围;
(3)将双曲线y=(x>0)先向下平移4个单位后得到Q2,再将Q2在x轴下方的图象沿x轴向上翻折与Q2在x轴上方的部分共同组成图象Q3.
①请在备用图中画出图象Q3;
②设直线y=a(0<a<4)与y轴及Q3分别交于点A,B,C(从左至右依次排列),若=,求a的值.
28.九年级数学(下)第26章《反比例函数》单元检测题(月考一)
(测试范围:第26章全章内容 考试时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.如图某一反比例函数的图象,它的函数解析式可能是( )
A.y= B.y=x2 C.y=2x D.y=-
答案:A
2.已知反比例函数y=的图象经过(1,-4),则k的值是( )
A.-4 B.4 C.2 D.-2
答案:A
3.若反比例函数的图象经过点(-2,3),则该反比例函数图象一定经过点( )
A.(2,3) B.(2,-3) C.(-2,-3) D.(-1,-6)
答案:B
4.已知甲、乙两地相距s(km),汽车从甲地行驶到乙地,则汽车行驶的时间t(h)与行驶速度(km/h)的函数关系图象大致是( )
A B C D
答案:B
5.如图,A是反比例函数y=的图象上的一点,AB⊥x轴于点B,且△ABO的面积是2,则k的值是( )
A.2 B.-2 C.-4 D.4
答案:D
6.正比例函数y=6x的图象与反比例函数y=的图象的交点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第一、三象限
答案:D
7.已知反比例函数y=-,下列结论中正确的是( )
A.图象经过点(-1,-1) B.图象在第一、三象限
C.当x>0时,0<y<1 D.当x<0时,y随x的增大而增大
答案:D
8.如图,正比例函数y=x与反比例函数y=的图象相交于A、B两点,BC⊥x轴于点C,则△ABC的面积为( )
A.1 B.1.5 C.2 D.2.5
答案:C
第8题图 第10题图
9.在反比例函数y=图象上有两点A(x1,y1),B(x2,y2),x1<0<x2,y1<y2,则m的取值范围是( )
A.m≥ B.m≤ C.m> D.m<
答案:D
10.如图,直线y=-x+5与双曲线y=(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是2.5.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=( x>0)的公共点有( )
A.0个 B.1个 C.2个 D.0个或1个或2个
答案:B
解:可求B(4,1),∴y=,将直线y=-x+5向下平移1个单位得y=-x+5-1=-x+4,联立y=-x+4与y=,整理得,x2-4x+4=0,∵△=(-4)2+4×4=0,∴平移后的直线与双曲线y=只有一个公共点.
二、填空题(每小题3分,共18分)
11.若一个反比例函数的图象位于一、三象限,则它的解析式可能是 .
答案:y=(写出一个即可)
12.如果两点P1(1,y1)和P2(2,y2)在反比例函数y=的图象上,那么y1 y2(填“>”“<”或“=”).
答案:>
13.已知反比例函数y=的图象经过点A(-2,3),则当x=-6时,y= .
答案:1
14.若反比例函数y=的图象位于第二、四象限,则k的取值范围是 .
答案:k <-2
15.如图,过点P(5,4)作PA⊥x轴于点A,PB⊥y轴于点B,且PA,PB分别与某双曲线上的一支交于点C,点D,则AC:BD的值为 .
答案:4:5
第15题图 第16题图
16.如图,直线y=k1x+3与双曲线y=(x>0)相交于点B(x1,y1),C(x2,y2)两点,若x2=2x1,则k1·k2的值为 .
解:联立k1x+3=,整理得k1x2+3x-k2=0,∴x1+x2=-,x1x2=-,∵x2=2x1,∴x1+x2=3x1=-,x1x2=2x12=-,∴-=(-)2,整理得k1k2=-2.
三、解答题(共8题,共72分)
17.(本题8分)反比例函数y=的图象经过点A(3,4).
(1)求k值;
(2)请判断点B(2,6)是否在这个反比例函数的图象上,并说明理由.
解:(1)k=12
(2)在.
18.(本题8分)如图,已知一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3)和B(-3,m)两点.
(1)求这两个函数的解析式;
(2)直接写出△AOB的面积 .
解:(1)y=,y=x+1;
(2)2.5.
19.(本题8分)如图,直线y=mx与双曲线y=相交于A,B两点,A点的坐标为(2,4).
(1)求反比例函数的解析式;
(2)直接写出线段AB的长是 .
解:(1)把A(2,4)代入y=得:k=8,即反比例函数的解析式是y=;
(2)过A作AC⊥x轴于C,∵A(2,4),∴AC=4,OC=2,由勾股定理得:AO=2,同理求出OB=2,∴AB=4.
20.(本题8分)已知直线y=-3x与双曲线y=交于点P(-1,n).
(1)求n,m的值;
(2)若点A(-3,y1),B(-1,y2)在双曲线y=上,比较y1,y2的大小.
解:(1)n=3,m=2;
(2)∵m-5=-3<0,∴当x<0时,y随x的增大而增大,
又∵点A(x1,y1),B(x2,y2)在双曲线y=上,且x1<x2<0,∴y1<y2.
21.(本题8分)如图,直线y=2x与双曲线y=在第一象限内交于点A(m,2),将直线y=2x向下平移后与反比例函数y=在第一象限内的图象交于点P,且△POA的面积为2.
(1)则k的值是 ;
(2)求平移后的直线的解析式.
解:(1)k=2;
(2)设平移后的直线与y轴交于点B,连接AB,则S△AOB=S△POA=2,求得OB=4,则平移后的直线的函数解析式y=2x-4.
22.(本题10分)如图,点B(3,3)在双曲线y=(x>0)上,点D在双曲线y=-(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(1)求k的值;
(2)求点A的坐标.
解:(1)∵点B(3,3)在双曲线y=上,∴k=3×3=9;
(2)过D作DM⊥x轴于M,过B作BN⊥y轴于N,则∠DMA=∠ANB=90°,
∵B(3,3),∴BN=ON=3,设MD=a,OM=b,
∵D在双曲线y=-(x<0)上,∴-ab=-4,ab=4,
∵四边形ABCD是正方形,证△ADM≌△BAN,
∴BN=AM=3,MD=AN=a,∴OA=3-a,
即ON=b+3-a=3,∴a=b=2,∴OA=3-2=1,∴A(1,0).
23.(本题10分)某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示.
第1天 第2天 第3天 第4天
售价x(元/双) 150 200 250 300
销售量y(双) 40 30 24 20
(1)观察表中数据x,y满足什么函数关系?请写出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
解:(1)由表中数据得xy=6000,∴y=,∴ y是x的反比例函数,故函数关系式为y=;
(2)由题意得(x-120)y=3000,把y=代入,
得(x-120)·=3000,解得x=240,经检验x=240是原方程的根.
答:若商场计划每天的销售利润为3000元,则其单价应定为240元.
24.(本题12分)如图,已知双曲线Q1:y=(m>0)经过点(-6,t)和点(4,t+1).
(1)求双曲线的解析式;
(2)若直线y=kx+8与Q1有且只有3个公共点,求k的取值范围;
(3)将双曲线y=(x>0)先向下平移4个单位后得到Q2,再将Q2在x轴下方的图象沿x轴向上翻折与Q2在x轴上方的部分共同组成图象Q3.
①请在备用图中画出图象Q3;
②设直线y=a(0<a<4)与y轴及Q3分别交于点A,B,C(从左至右依次排列),若=,求a的值.
解:(1)y=;
(2)联立得:kx2+8x-12=0,由△=0得k=-,
联立得:kx2+8x+12=0,由△=0得k=,
∵直线y=kx+8与双曲线y=有且只有3个公共点,
∴0<k<或-<k<0;
(3)①画图略;②由题意,得:Q3的解析式为y=,
令y=a,则A(0,a),B (,a),C (,a),
∵BC=2AB,∴-=2×,
解得:a=2,∴a的值为2.
21世纪教育网(www.21cnjy.com)
28.九年级数学(下)第26章《反比例函数》单元检测题(月考一)
(测试范围:第26章全章内容 考试时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.如图某一反比例函数的图象,它的函数解析式可能是( )
A.y= B.y=x2 C.y=2x D.y=-
2.已知反比例函数y=的图象经过(1,-4),则k的值是( )
A.-4 B.4 C.2 D.-2
3.若反比例函数的图象经过点(-2,3),则该反比例函数图象一定经过点( )
A.(2,3) B.(2,-3) C.(-2,-3) D.(-1,-6)
4.已知甲、乙两地相距s(km),汽车从甲地行驶到乙地,则汽车行驶的时间t(h)与行驶速度(km/h)的函数关系图象大致是( )
A B C D
5.如图,A是反比例函数y=的图象上的一点,AB⊥x轴于点B,且△ABO的面积是2,则k的值是( )
A.2 B.-2 C.-4 D.4
6.正比例函数y=6x的图象与反比例函数y=的图象的交点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第一、三象限
7.已知反比例函数y=-,下列结论中正确的是( )
A.图象经过点(-1,-1) B.图象在第一、三象限
C.当x>0时,0<y<1 D.当x<0时,y随x的增大而增大
8.如图,正比例函数y=x与反比例函数y=的图象相交于A、B两点,BC⊥x轴于点C,则△ABC的面积为( )
A.1 B.1.5 C.2 D.2.5
第8题图 第10题图
9.在反比例函数y=图象上有两点A(x1,y1),B(x2,y2),x1<0<x2,y1<y2,则m的取值范围是( )
A.m≥ B.m≤ C.m> D.m<
10.如图,直线y=-x+5与双曲线y=(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是2.5.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=( x>0)的公共点有( )
A.0个 B.1个 C.2个 D.0个或1个或2个
二、填空题(每小题3分,共18分)
11.若一个反比例函数的图象位于一、三象限,则它的解析式可能是 .
12.如果两点P1(1,y1)和P2(2,y2)在反比例函数y=的图象上,那么y1 y2(填“>”“<”或“=”).
13.已知反比例函数y=的图象经过点A(-2,3),则当x=-6时,y= .
14.若反比例函数y=的图象位于第二、四象限,则k的取值范围是 .
15.如图,过点P(5,4)作PA⊥x轴于点A,PB⊥y轴于点B,且PA,PB分别与某双曲线上的一支交于点C,点D,则AC:BD的值为 .
第15题图 第16题图
16.如图,直线y=k1x+3与双曲线y=(x>0)相交于点B(x1,y1),C(x2,y2)两点,若x2=2x1,则k1·k2的值为 .
三、解答题(共8题,共72分)
17.(本题8分)反比例函数y=的图象经过点A(3,4).
(1)求k值;
(2)请判断点B(2,6)是否在这个反比例函数的图象上,并说明理由.
18.(本题8分)如图,已知一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3)和B(-3,m)两点.
(1)求这两个函数的解析式;
(2)直接写出△AOB的面积 .
19.(本题8分)如图,直线y=mx与双曲线y=相交于A,B两点,A点的坐标为(2,4).
(1)求反比例函数的解析式;
(2)直接写出线段AB的长是 .
20.(本题8分)已知直线y=-3x与双曲线y=交于点P(-1,n).
(1)求n,m的值;
(2)若点A(-3,y1),B(-1,y2)在双曲线y=上,比较y1,y2的大小.
21.(本题8分)如图,直线y=2x与双曲线y=在第一象限内交于点A(m,2),将直线y=2x向下平移后与反比例函数y=在第一象限内的图象交于点P,且△POA的面积为2.
(1)则k的值是 ;
(2)求平移后的直线的解析式.
22.(本题10分)如图,点B(3,3)在双曲线y=(x>0)上,点D在双曲线y=-(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(1)求k的值;
(2)求点A的坐标.
23.(本题10分)某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示.
第1天 第2天 第3天 第4天
售价x(元/双) 150 200 250 300
销售量y(双) 40 30 24 20
(1)观察表中数据x,y满足什么函数关系?请写出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
24.(本题12分)如图,已知双曲线Q1:y=(m>0)经过点(-6,t)和点(4,t+1).
(1)求双曲线的解析式;
(2)若直线y=kx+8与Q1有且只有3个公共点,求k的取值范围;
(3)将双曲线y=(x>0)先向下平移4个单位后得到Q2,再将Q2在x轴下方的图象沿x轴向上翻折与Q2在x轴上方的部分共同组成图象Q3.
①请在备用图中画出图象Q3;
②设直线y=a(0<a<4)与y轴及Q3分别交于点A,B,C(从左至右依次排列),若=,求a的值.
28.九年级数学(下)第26章《反比例函数》单元检测题(月考一)
(测试范围:第26章全章内容 考试时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.如图某一反比例函数的图象,它的函数解析式可能是( )
A.y= B.y=x2 C.y=2x D.y=-
答案:A
2.已知反比例函数y=的图象经过(1,-4),则k的值是( )
A.-4 B.4 C.2 D.-2
答案:A
3.若反比例函数的图象经过点(-2,3),则该反比例函数图象一定经过点( )
A.(2,3) B.(2,-3) C.(-2,-3) D.(-1,-6)
答案:B
4.已知甲、乙两地相距s(km),汽车从甲地行驶到乙地,则汽车行驶的时间t(h)与行驶速度(km/h)的函数关系图象大致是( )
A B C D
答案:B
5.如图,A是反比例函数y=的图象上的一点,AB⊥x轴于点B,且△ABO的面积是2,则k的值是( )
A.2 B.-2 C.-4 D.4
答案:D
6.正比例函数y=6x的图象与反比例函数y=的图象的交点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第一、三象限
答案:D
7.已知反比例函数y=-,下列结论中正确的是( )
A.图象经过点(-1,-1) B.图象在第一、三象限
C.当x>0时,0<y<1 D.当x<0时,y随x的增大而增大
答案:D
8.如图,正比例函数y=x与反比例函数y=的图象相交于A、B两点,BC⊥x轴于点C,则△ABC的面积为( )
A.1 B.1.5 C.2 D.2.5
答案:C
第8题图 第10题图
9.在反比例函数y=图象上有两点A(x1,y1),B(x2,y2),x1<0<x2,y1<y2,则m的取值范围是( )
A.m≥ B.m≤ C.m> D.m<
答案:D
10.如图,直线y=-x+5与双曲线y=(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是2.5.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=( x>0)的公共点有( )
A.0个 B.1个 C.2个 D.0个或1个或2个
答案:B
解:可求B(4,1),∴y=,将直线y=-x+5向下平移1个单位得y=-x+5-1=-x+4,联立y=-x+4与y=,整理得,x2-4x+4=0,∵△=(-4)2+4×4=0,∴平移后的直线与双曲线y=只有一个公共点.
二、填空题(每小题3分,共18分)
11.若一个反比例函数的图象位于一、三象限,则它的解析式可能是 .
答案:y=(写出一个即可)
12.如果两点P1(1,y1)和P2(2,y2)在反比例函数y=的图象上,那么y1 y2(填“>”“<”或“=”).
答案:>
13.已知反比例函数y=的图象经过点A(-2,3),则当x=-6时,y= .
答案:1
14.若反比例函数y=的图象位于第二、四象限,则k的取值范围是 .
答案:k <-2
15.如图,过点P(5,4)作PA⊥x轴于点A,PB⊥y轴于点B,且PA,PB分别与某双曲线上的一支交于点C,点D,则AC:BD的值为 .
答案:4:5
第15题图 第16题图
16.如图,直线y=k1x+3与双曲线y=(x>0)相交于点B(x1,y1),C(x2,y2)两点,若x2=2x1,则k1·k2的值为 .
解:联立k1x+3=,整理得k1x2+3x-k2=0,∴x1+x2=-,x1x2=-,∵x2=2x1,∴x1+x2=3x1=-,x1x2=2x12=-,∴-=(-)2,整理得k1k2=-2.
三、解答题(共8题,共72分)
17.(本题8分)反比例函数y=的图象经过点A(3,4).
(1)求k值;
(2)请判断点B(2,6)是否在这个反比例函数的图象上,并说明理由.
解:(1)k=12
(2)在.
18.(本题8分)如图,已知一次函数y=kx+b的图象与反比例函数y=的图象交于A(2,3)和B(-3,m)两点.
(1)求这两个函数的解析式;
(2)直接写出△AOB的面积 .
解:(1)y=,y=x+1;
(2)2.5.
19.(本题8分)如图,直线y=mx与双曲线y=相交于A,B两点,A点的坐标为(2,4).
(1)求反比例函数的解析式;
(2)直接写出线段AB的长是 .
解:(1)把A(2,4)代入y=得:k=8,即反比例函数的解析式是y=;
(2)过A作AC⊥x轴于C,∵A(2,4),∴AC=4,OC=2,由勾股定理得:AO=2,同理求出OB=2,∴AB=4.
20.(本题8分)已知直线y=-3x与双曲线y=交于点P(-1,n).
(1)求n,m的值;
(2)若点A(-3,y1),B(-1,y2)在双曲线y=上,比较y1,y2的大小.
解:(1)n=3,m=2;
(2)∵m-5=-3<0,∴当x<0时,y随x的增大而增大,
又∵点A(x1,y1),B(x2,y2)在双曲线y=上,且x1<x2<0,∴y1<y2.
21.(本题8分)如图,直线y=2x与双曲线y=在第一象限内交于点A(m,2),将直线y=2x向下平移后与反比例函数y=在第一象限内的图象交于点P,且△POA的面积为2.
(1)则k的值是 ;
(2)求平移后的直线的解析式.
解:(1)k=2;
(2)设平移后的直线与y轴交于点B,连接AB,则S△AOB=S△POA=2,求得OB=4,则平移后的直线的函数解析式y=2x-4.
22.(本题10分)如图,点B(3,3)在双曲线y=(x>0)上,点D在双曲线y=-(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(1)求k的值;
(2)求点A的坐标.
解:(1)∵点B(3,3)在双曲线y=上,∴k=3×3=9;
(2)过D作DM⊥x轴于M,过B作BN⊥y轴于N,则∠DMA=∠ANB=90°,
∵B(3,3),∴BN=ON=3,设MD=a,OM=b,
∵D在双曲线y=-(x<0)上,∴-ab=-4,ab=4,
∵四边形ABCD是正方形,证△ADM≌△BAN,
∴BN=AM=3,MD=AN=a,∴OA=3-a,
即ON=b+3-a=3,∴a=b=2,∴OA=3-2=1,∴A(1,0).
23.(本题10分)某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示.
第1天 第2天 第3天 第4天
售价x(元/双) 150 200 250 300
销售量y(双) 40 30 24 20
(1)观察表中数据x,y满足什么函数关系?请写出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
解:(1)由表中数据得xy=6000,∴y=,∴ y是x的反比例函数,故函数关系式为y=;
(2)由题意得(x-120)y=3000,把y=代入,
得(x-120)·=3000,解得x=240,经检验x=240是原方程的根.
答:若商场计划每天的销售利润为3000元,则其单价应定为240元.
24.(本题12分)如图,已知双曲线Q1:y=(m>0)经过点(-6,t)和点(4,t+1).
(1)求双曲线的解析式;
(2)若直线y=kx+8与Q1有且只有3个公共点,求k的取值范围;
(3)将双曲线y=(x>0)先向下平移4个单位后得到Q2,再将Q2在x轴下方的图象沿x轴向上翻折与Q2在x轴上方的部分共同组成图象Q3.
①请在备用图中画出图象Q3;
②设直线y=a(0<a<4)与y轴及Q3分别交于点A,B,C(从左至右依次排列),若=,求a的值.
解:(1)y=;
(2)联立得:kx2+8x-12=0,由△=0得k=-,
联立得:kx2+8x+12=0,由△=0得k=,
∵直线y=kx+8与双曲线y=有且只有3个公共点,
∴0<k<或-<k<0;
(3)①画图略;②由题意,得:Q3的解析式为y=,
令y=a,则A(0,a),B (,a),C (,a),
∵BC=2AB,∴-=2×,
解得:a=2,∴a的值为2.
21世纪教育网(www.21cnjy.com)
