29.九年级数学(下)第27章《相似》周练(一)(含答案)
文档属性
| 名称 | 29.九年级数学(下)第27章《相似》周练(一)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 293.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 19:40:28 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
29.九年级数学(下)第27章《相似》周练(一)
(考试范围:第27.1~27.2 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
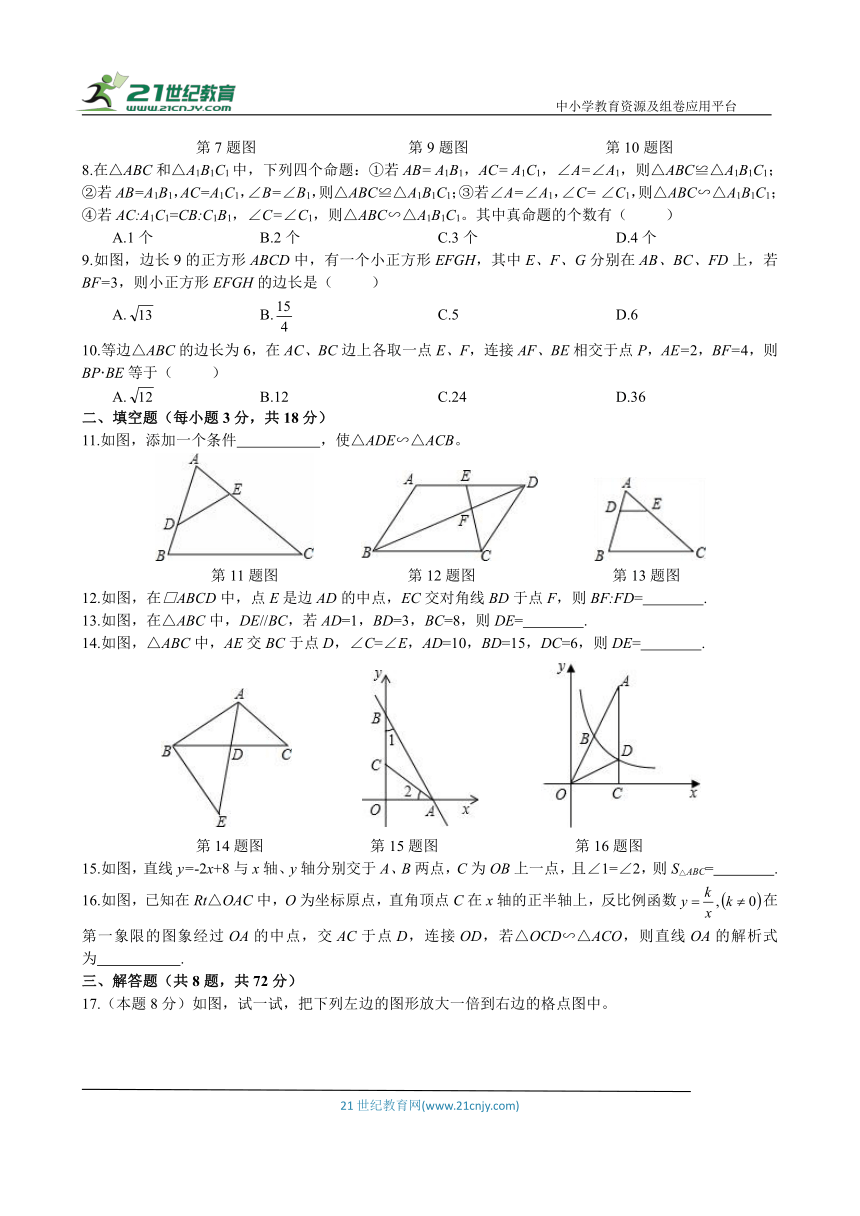
1.小张用手机拍摄得到甲图,经放大后得到乙图,甲图中的线段AB在乙图中对应线段是( )
A.FG B.FH C.EH D.EF
第1题图 第2题图 第3题图
2.如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,若取黄金比为0.6,则x的值为( )
A.108 B.120 C.135 D.216
3.如图,已知直线a//b//c,直线m、n与a、b、c分别交于点A、C、E、B、D、F,AC=8,CE=12,BD=6,则DF等于( )
A.4 B.5 C.9 D.7
4.如图,△ABC∽△AED,那么AE·BC等于( )
A.AB·DE B.AC·DE C.AC·AE D.AB·AE
第4题图 第5题图 第6题图
5.如图,在正方形网格上有两个△ABC和△DEF相似,则∠BAC的度数为( )
A.105° B.115° C.125° D.135°
6.如图,△ACP∽△ABC,若∠A=100°,∠ACP=20°,则∠ACB的度数是( )
A.80° B.60° C.50° D.30°
7.如图,在□ABCD中,EF//AB,DE:EA=2:3,EF=4,则CD的长为( )
A.6 B.8 C.9 D.10
第7题图 第9题图 第10题图
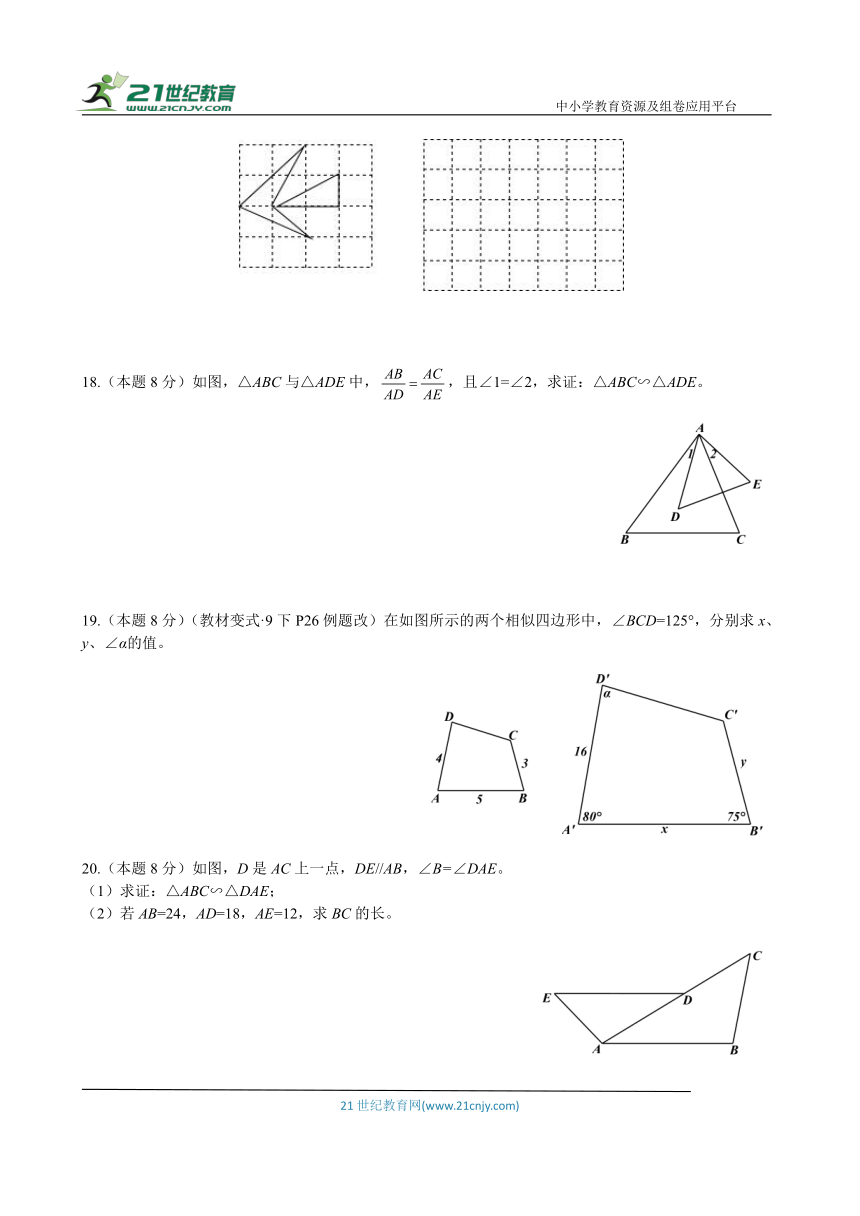
8.在△ABC和△A1B1C1中,下列四个命题:①若AB= A1B1,AC= A1C1,∠A=∠A1,则△ABC≌△A1B1C1;②若AB=A1B1,AC=A1C1,∠B=∠B1,则△ABC≌△A1B1C1;③若∠A=∠A1,∠C= ∠C1,则△ABC∽△A1B1C1;④若AC:A1C1=CB:C1B1,∠C=∠C1,则△ABC∽△A1B1C1。其中真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
9.如图,边长9的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形EFGH的边长是( )
A. B. C.5 D.6
10.等边△ABC的边长为6,在AC、BC边上各取一点E、F,连接AF、BE相交于点P,AE=2,BF=4,则BP·BE等于( )
A. B.12 C.24 D.36
二、填空题(每小题3分,共18分)
11.如图,添加一个条件 ,使△ADE∽△ACB。
第11题图 第12题图 第13题图
12.如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则BF:FD= .
13.如图,在△ABC中,DE//BC,若AD=1,BD=3,BC=8,则DE= .
14.如图,△ABC中,AE交BC于点D,∠C=∠E,AD=10,BD=15,DC=6,则DE= .
第14题图 第15题图 第16题图
15.如图,直线y=-2x+8与x轴、y轴分别交于A、B两点,C为OB上一点,且∠1=∠2,则S△ABC= .
16.如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数在第一象限的图象经过OA的中点,交AC于点D,连接OD,若△OCD∽△ACO,则直线OA的解析式为 .
三、解答题(共8题,共72分)
17.(本题8分)如图,试一试,把下列左边的图形放大一倍到右边的格点图中。
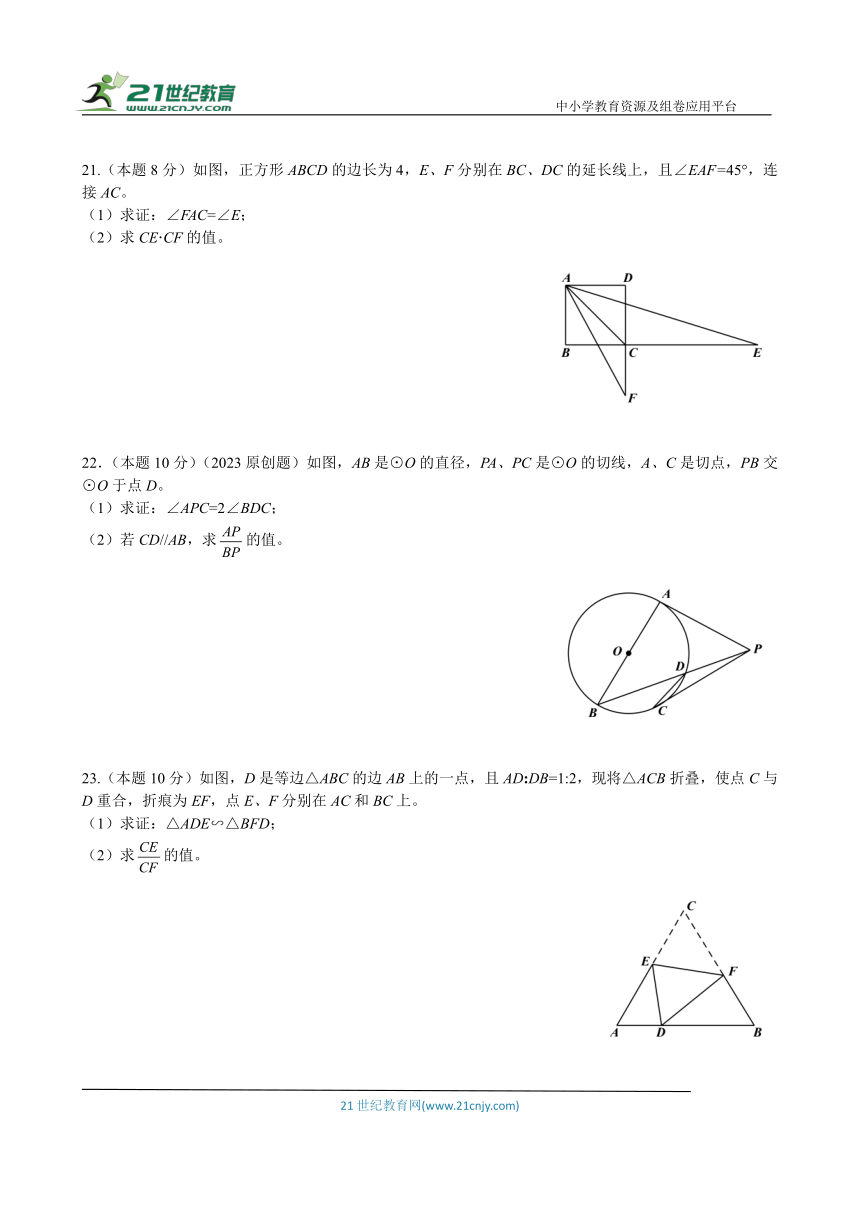
18.(本题8分)如图,△ABC与△ADE中,,且∠1=∠2,求证:△ABC∽△ADE。
19.(本题8分)(教材变式·9下P26例题改)在如图所示的两个相似四边形中,∠BCD=125°,分别求x、y、∠α的值。
20.(本题8分)如图,D是AC上一点,DE//AB,∠B=∠DAE。
(1)求证:△ABC∽△DAE;
(2)若AB=24,AD=18,AE=12,求BC的长。
21.(本题8分)如图,正方形ABCD的边长为4,E、F分别在BC、DC的延长线上,且∠EAF=45°,连接AC。
(1)求证:∠FAC=∠E;
(2)求CE·CF的值。
22.(本题10分)(2023原创题)如图,AB是⊙O的直径,PA、PC是⊙O的切线,A、C是切点,PB交⊙O于点D。
(1)求证:∠APC=2∠BDC;
(2)若CD//AB,求的值。
23.(本题10分)如图,D是等边△ABC的边AB上的一点,且AD:DB=1:2,现将△ACB折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上。
(1)求证:△ADE∽△BFD;
(2)求的值。
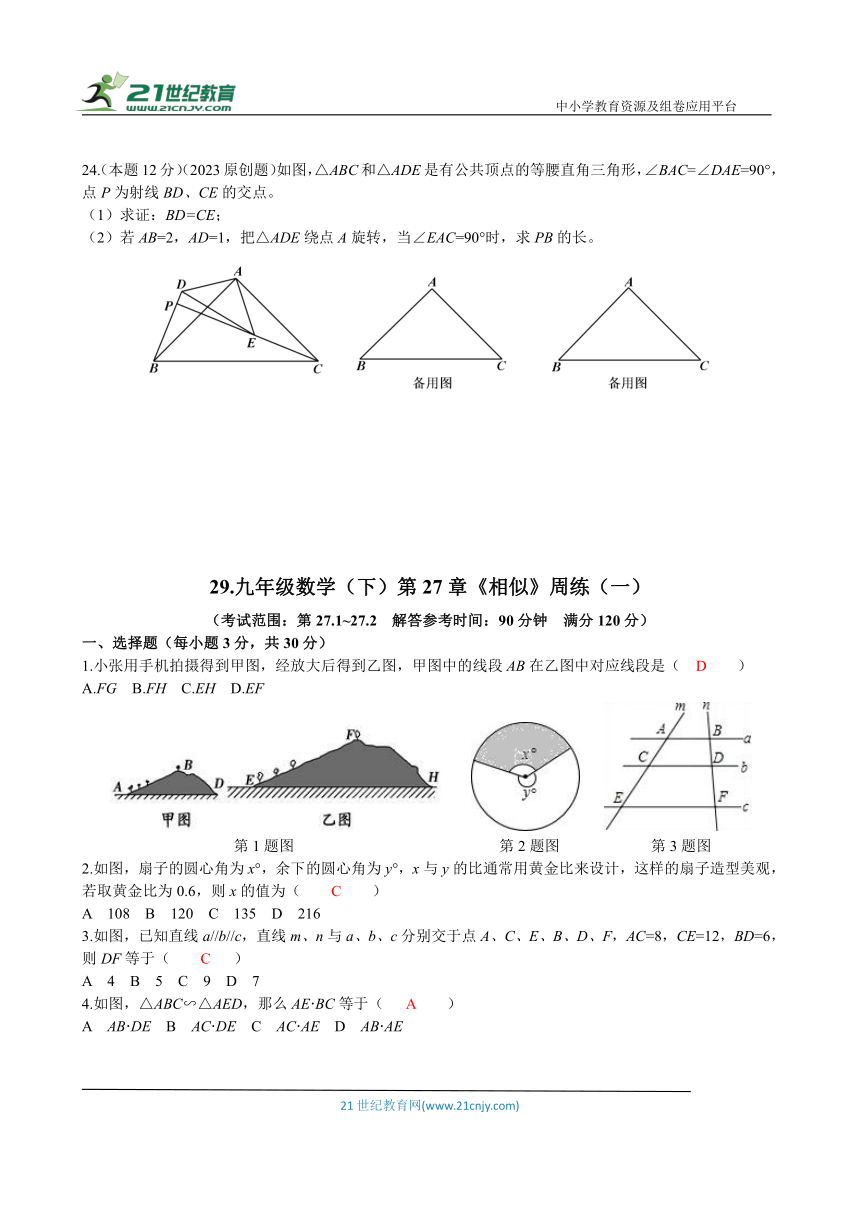
24.(本题12分)(2023原创题)如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD、CE的交点。
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长。
29.九年级数学(下)第27章《相似》周练(一)
(考试范围:第27.1~27.2 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
1.小张用手机拍摄得到甲图,经放大后得到乙图,甲图中的线段AB在乙图中对应线段是( D )
A.FG B.FH C.EH D.EF
第1题图 第2题图 第3题图
2.如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,若取黄金比为0.6,则x的值为( C )
A 108 B 120 C 135 D 216
3.如图,已知直线a//b//c,直线m、n与a、b、c分别交于点A、C、E、B、D、F,AC=8,CE=12,BD=6,则DF等于( C )
A 4 B 5 C 9 D 7
4.如图,△ABC∽△AED,那么AE·BC等于( A )
A AB·DE B AC·DE C AC·AE D AB·AE
第4题图 第5题图 第6题图
5.如图,在正方形网格上有两个△ABC和△DEF相似,则∠BAC的度数为( D )
A 105° B 115° C 125° D 135°
6.如图,△ACP∽△ABC,若∠A=100°,∠ACP=20°,则∠ACB的度数是( B )
A 80° B 60° C 50° D 30°
7.如图,在□ABCD中,EF//AB,DE:EA=2:3,EF=4,则CD的长为( D )
A 6 B 8 C 9 D 10
第7题图 第9题图 第10题图
8.在△ABC和△A1B1C1中,下列四个命题:①若AB= A1B1,AC= A1C1,∠A=∠A1,则△ABC≌△A1B1C1;②若AB=A1B1,AC=A1C1,∠B=∠B1,则△ABC≌△A1B1C1;③若∠A=∠A1,∠C= ∠C1,则△ABC∽△A1B1C1;④若AC:A1C1=CB:C1B1,∠C=∠C1,则△ABC∽△A1B1C1。其中真命题的个数有( C )
A 1个 B 2个 C 3个 D 4个
9.如图,边长9的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形EFGH的边长是( A )
A B C 5 D 6
10.等边△ABC的边长为6,在AC、BC边上各取一点E、F,连接AF、BE相交于点P,AE=2,BF=4,则BP·BE等于( C )
A B 12 C 24 D 36
二、填空题(每小题3分,共18分)
11.如图,添加一个条件 ∠ADE=∠ACB ,使△ADE∽△ACB。
第11题图 第12题图 第13题图
12.如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则BF:FD= 2:1 。
13.如图,在△ABC中,DE//BC,若AD=1,BD=3,BC=8,则DE= 2 。
14.如图,△ABC中,AE交BC于点D,∠C=∠E,AD=10,BD=15,DC=6,则DE= 9 。
第14题图 第15题图 第16题图
15.如图,直线y=-2x+8与x轴、y轴分别交于A、B两点,C为OB上一点,且∠1=∠2,则S△ABC= 12 。
16.如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数在第一象限的图象经过OA的中点,交AC于点D,连接OD,若△OCD∽△ACO,则直线OA的解析式为 y=2x 。
三、解答题(共8题,共72分)
17.(本题8分)如图,试一试,把下列左边的图形放大一倍到右边的格点图中。
解:略。
18.(本题8分)如图,△ABC与△ADE中,,且∠1=∠2,求证:△ABC∽△ADE。
证:∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC,∴∠BAC=∠DAE,∵AB:AD=AC:AE,∴△ABC∽△ADE。
19.(本题8分)(教材变式·9下P26例题改)在如图所示的两个相似四边形中,∠BCD=125°,分别求x、y、∠α的值。
解:由相似多边形的性质可得:①∠C’=125°,∴α=360°-80°-75°-125°=80°;②,即,∴x=20,y=12。
20.(本题8分)如图,D是AC上一点,DE//AB,∠B=∠DAE。
(1)求证:△ABC∽△DAE;
(2)若AB=24,AD=18,AE=12,求BC的长。
解:(1)略;
(2)BC=16.
21.(本题8分)如图,正方形ABCD的边长为4,E、F分别在BC、DC的延长线上,且∠EAF=45°,连接AC。
(1)求证:∠FAC=∠E;
(2)求CE·CF的值。
解:(1)∵∠FAC+∠CAE=∠E+∠CAE=45°,∴∠FAC=∠E;
(2)易证△ACE∽△FCA,∴CE·CF=AC2=32。
22.(本题10分)(2023原创题)如图,AB是⊙O的直径,PA、PC是⊙O的切线,A、C是切点,PB交⊙O于点D。
(1)求证:∠APC=2∠BDC;
(2)若CD//AB,求的值。
解:(1)连OP、AC,证∠BDC=∠BAC=∠APO=∠CPO即可;
(2)证∠B=∠BDC=∠BAC=∠APO,∴△APB∽△AOP,∴,设⊙O的半径为R,则,∴,∴BP=,∴。
23.(本题10分)如图,D是等边△ABC的边AB上的一点,且AD:DB=1:2,现将△ACB折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上。
(1)求证:△ADE∽△BFD;
(2)求的值。
解:(1)证∠ADE+∠BDF=∠DFB+∠BDF=120°,∴∠ADE=∠BFD,∴△ADE∽△BFD。
(2)设,则CE:CF=k,设CF=x,则CE=kx,由AD:DB=1:2可设AD=1,DB=2,∴AE=3-kx,BF=3-x代入得,解得,即。
24.(本题12分)(2023原创题)如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD、CE的交点。
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长。
解:(1)∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∠DAB=90°-∠BAE=∠EAC,∴△ADB≌△AEC,∴BD=CE。
(2)①当点E在AB上时,BE=AB-AE=1,∵∠EAC=90°,∴CE=,同(1)可证△ADB≌△AEC,∴∠DBA=∠ECA,∵∠PEB=∠AEC,∴△PEB∽△AEC,∴,∴,∴PB=。
②当点E在BA延长线上时,BE=3,∵∠EAC=90°,∴CE=,同(1)可证△ADB≌△AEC,∴∠DBA=∠ECA,∵∠BEP=∠CEA,∴△PEB∽△AEC,∴,∴,∴PB=,综上,PB=或。
21世纪教育网(www.21cnjy.com)
29.九年级数学(下)第27章《相似》周练(一)
(考试范围:第27.1~27.2 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
1.小张用手机拍摄得到甲图,经放大后得到乙图,甲图中的线段AB在乙图中对应线段是( )
A.FG B.FH C.EH D.EF
第1题图 第2题图 第3题图
2.如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,若取黄金比为0.6,则x的值为( )
A.108 B.120 C.135 D.216
3.如图,已知直线a//b//c,直线m、n与a、b、c分别交于点A、C、E、B、D、F,AC=8,CE=12,BD=6,则DF等于( )
A.4 B.5 C.9 D.7
4.如图,△ABC∽△AED,那么AE·BC等于( )
A.AB·DE B.AC·DE C.AC·AE D.AB·AE
第4题图 第5题图 第6题图
5.如图,在正方形网格上有两个△ABC和△DEF相似,则∠BAC的度数为( )
A.105° B.115° C.125° D.135°
6.如图,△ACP∽△ABC,若∠A=100°,∠ACP=20°,则∠ACB的度数是( )
A.80° B.60° C.50° D.30°
7.如图,在□ABCD中,EF//AB,DE:EA=2:3,EF=4,则CD的长为( )
A.6 B.8 C.9 D.10
第7题图 第9题图 第10题图
8.在△ABC和△A1B1C1中,下列四个命题:①若AB= A1B1,AC= A1C1,∠A=∠A1,则△ABC≌△A1B1C1;②若AB=A1B1,AC=A1C1,∠B=∠B1,则△ABC≌△A1B1C1;③若∠A=∠A1,∠C= ∠C1,则△ABC∽△A1B1C1;④若AC:A1C1=CB:C1B1,∠C=∠C1,则△ABC∽△A1B1C1。其中真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
9.如图,边长9的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形EFGH的边长是( )
A. B. C.5 D.6
10.等边△ABC的边长为6,在AC、BC边上各取一点E、F,连接AF、BE相交于点P,AE=2,BF=4,则BP·BE等于( )
A. B.12 C.24 D.36
二、填空题(每小题3分,共18分)
11.如图,添加一个条件 ,使△ADE∽△ACB。
第11题图 第12题图 第13题图
12.如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则BF:FD= .
13.如图,在△ABC中,DE//BC,若AD=1,BD=3,BC=8,则DE= .
14.如图,△ABC中,AE交BC于点D,∠C=∠E,AD=10,BD=15,DC=6,则DE= .
第14题图 第15题图 第16题图
15.如图,直线y=-2x+8与x轴、y轴分别交于A、B两点,C为OB上一点,且∠1=∠2,则S△ABC= .
16.如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数在第一象限的图象经过OA的中点,交AC于点D,连接OD,若△OCD∽△ACO,则直线OA的解析式为 .
三、解答题(共8题,共72分)
17.(本题8分)如图,试一试,把下列左边的图形放大一倍到右边的格点图中。
18.(本题8分)如图,△ABC与△ADE中,,且∠1=∠2,求证:△ABC∽△ADE。
19.(本题8分)(教材变式·9下P26例题改)在如图所示的两个相似四边形中,∠BCD=125°,分别求x、y、∠α的值。
20.(本题8分)如图,D是AC上一点,DE//AB,∠B=∠DAE。
(1)求证:△ABC∽△DAE;
(2)若AB=24,AD=18,AE=12,求BC的长。
21.(本题8分)如图,正方形ABCD的边长为4,E、F分别在BC、DC的延长线上,且∠EAF=45°,连接AC。
(1)求证:∠FAC=∠E;
(2)求CE·CF的值。
22.(本题10分)(2023原创题)如图,AB是⊙O的直径,PA、PC是⊙O的切线,A、C是切点,PB交⊙O于点D。
(1)求证:∠APC=2∠BDC;
(2)若CD//AB,求的值。
23.(本题10分)如图,D是等边△ABC的边AB上的一点,且AD:DB=1:2,现将△ACB折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上。
(1)求证:△ADE∽△BFD;
(2)求的值。
24.(本题12分)(2023原创题)如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD、CE的交点。
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长。
29.九年级数学(下)第27章《相似》周练(一)
(考试范围:第27.1~27.2 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
1.小张用手机拍摄得到甲图,经放大后得到乙图,甲图中的线段AB在乙图中对应线段是( D )
A.FG B.FH C.EH D.EF
第1题图 第2题图 第3题图
2.如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,若取黄金比为0.6,则x的值为( C )
A 108 B 120 C 135 D 216
3.如图,已知直线a//b//c,直线m、n与a、b、c分别交于点A、C、E、B、D、F,AC=8,CE=12,BD=6,则DF等于( C )
A 4 B 5 C 9 D 7
4.如图,△ABC∽△AED,那么AE·BC等于( A )
A AB·DE B AC·DE C AC·AE D AB·AE
第4题图 第5题图 第6题图
5.如图,在正方形网格上有两个△ABC和△DEF相似,则∠BAC的度数为( D )
A 105° B 115° C 125° D 135°
6.如图,△ACP∽△ABC,若∠A=100°,∠ACP=20°,则∠ACB的度数是( B )
A 80° B 60° C 50° D 30°
7.如图,在□ABCD中,EF//AB,DE:EA=2:3,EF=4,则CD的长为( D )
A 6 B 8 C 9 D 10
第7题图 第9题图 第10题图
8.在△ABC和△A1B1C1中,下列四个命题:①若AB= A1B1,AC= A1C1,∠A=∠A1,则△ABC≌△A1B1C1;②若AB=A1B1,AC=A1C1,∠B=∠B1,则△ABC≌△A1B1C1;③若∠A=∠A1,∠C= ∠C1,则△ABC∽△A1B1C1;④若AC:A1C1=CB:C1B1,∠C=∠C1,则△ABC∽△A1B1C1。其中真命题的个数有( C )
A 1个 B 2个 C 3个 D 4个
9.如图,边长9的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形EFGH的边长是( A )
A B C 5 D 6
10.等边△ABC的边长为6,在AC、BC边上各取一点E、F,连接AF、BE相交于点P,AE=2,BF=4,则BP·BE等于( C )
A B 12 C 24 D 36
二、填空题(每小题3分,共18分)
11.如图,添加一个条件 ∠ADE=∠ACB ,使△ADE∽△ACB。
第11题图 第12题图 第13题图
12.如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则BF:FD= 2:1 。
13.如图,在△ABC中,DE//BC,若AD=1,BD=3,BC=8,则DE= 2 。
14.如图,△ABC中,AE交BC于点D,∠C=∠E,AD=10,BD=15,DC=6,则DE= 9 。
第14题图 第15题图 第16题图
15.如图,直线y=-2x+8与x轴、y轴分别交于A、B两点,C为OB上一点,且∠1=∠2,则S△ABC= 12 。
16.如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数在第一象限的图象经过OA的中点,交AC于点D,连接OD,若△OCD∽△ACO,则直线OA的解析式为 y=2x 。
三、解答题(共8题,共72分)
17.(本题8分)如图,试一试,把下列左边的图形放大一倍到右边的格点图中。
解:略。
18.(本题8分)如图,△ABC与△ADE中,,且∠1=∠2,求证:△ABC∽△ADE。
证:∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC,∴∠BAC=∠DAE,∵AB:AD=AC:AE,∴△ABC∽△ADE。
19.(本题8分)(教材变式·9下P26例题改)在如图所示的两个相似四边形中,∠BCD=125°,分别求x、y、∠α的值。
解:由相似多边形的性质可得:①∠C’=125°,∴α=360°-80°-75°-125°=80°;②,即,∴x=20,y=12。
20.(本题8分)如图,D是AC上一点,DE//AB,∠B=∠DAE。
(1)求证:△ABC∽△DAE;
(2)若AB=24,AD=18,AE=12,求BC的长。
解:(1)略;
(2)BC=16.
21.(本题8分)如图,正方形ABCD的边长为4,E、F分别在BC、DC的延长线上,且∠EAF=45°,连接AC。
(1)求证:∠FAC=∠E;
(2)求CE·CF的值。
解:(1)∵∠FAC+∠CAE=∠E+∠CAE=45°,∴∠FAC=∠E;
(2)易证△ACE∽△FCA,∴CE·CF=AC2=32。
22.(本题10分)(2023原创题)如图,AB是⊙O的直径,PA、PC是⊙O的切线,A、C是切点,PB交⊙O于点D。
(1)求证:∠APC=2∠BDC;
(2)若CD//AB,求的值。
解:(1)连OP、AC,证∠BDC=∠BAC=∠APO=∠CPO即可;
(2)证∠B=∠BDC=∠BAC=∠APO,∴△APB∽△AOP,∴,设⊙O的半径为R,则,∴,∴BP=,∴。
23.(本题10分)如图,D是等边△ABC的边AB上的一点,且AD:DB=1:2,现将△ACB折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上。
(1)求证:△ADE∽△BFD;
(2)求的值。
解:(1)证∠ADE+∠BDF=∠DFB+∠BDF=120°,∴∠ADE=∠BFD,∴△ADE∽△BFD。
(2)设,则CE:CF=k,设CF=x,则CE=kx,由AD:DB=1:2可设AD=1,DB=2,∴AE=3-kx,BF=3-x代入得,解得,即。
24.(本题12分)(2023原创题)如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD、CE的交点。
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长。
解:(1)∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∠DAB=90°-∠BAE=∠EAC,∴△ADB≌△AEC,∴BD=CE。
(2)①当点E在AB上时,BE=AB-AE=1,∵∠EAC=90°,∴CE=,同(1)可证△ADB≌△AEC,∴∠DBA=∠ECA,∵∠PEB=∠AEC,∴△PEB∽△AEC,∴,∴,∴PB=。
②当点E在BA延长线上时,BE=3,∵∠EAC=90°,∴CE=,同(1)可证△ADB≌△AEC,∴∠DBA=∠ECA,∵∠BEP=∠CEA,∴△PEB∽△AEC,∴,∴,∴PB=,综上,PB=或。
21世纪教育网(www.21cnjy.com)
