30.九年级数学(下)第27章《相似》周练(二)(含答案)
文档属性
| 名称 | 30.九年级数学(下)第27章《相似》周练(二)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 538.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 19:41:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
30.九年级数学(下)第27章《相似》周练(二)
(考试范围:第27.2∽27.3 解答参考时间:90分钟 满分120分)
一选择题(每小题3分,共30分)
1.已知△ABC∽△DEF,且相似比AB:DE=1:4,则△ABC与△DEF的对应高之比为( )
A.1:2 B.2:1 C.1:4 D.4:1
2.若△ABC∽△A′B′C′,且相似比为2:1,则△ABC与△A′B′C′的周长之比为( )
A.1:2 B.2:1 C.1:4 D.4:1
3.如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( )
A.1:3 B.2:3 C.1:4 D.1:2
4.如图,在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,0) B.(2,1) C.(3,3) D.(3,1)
5.(教材变式·9下P57习题7改)如图,零件的外径为17cm,要求它的壁厚x,需要先求出内径AB,现用一个交叉钳(AC与BD相等)去量,若测得OA:OC=OB:OD=3:1,CD=5cm,零件的壁厚x等于( )
A.2cm B.1cm C.0.5cm D.3cm
6.如图,在□ABCD中E为CD上一点,连接AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:DC等于( )
7.如图,D是△ABC的边BC上一点,已知AB=4,AD=2.∠DAC=∠B,若△ABD的面积为9,则△ACD的面积为( )
A.2 B.3 C.4 D.6
8.如图,在等边△ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )
A.2:3 B. :2 C. :3 D.1:3
第8题图 第9题图 第10题图
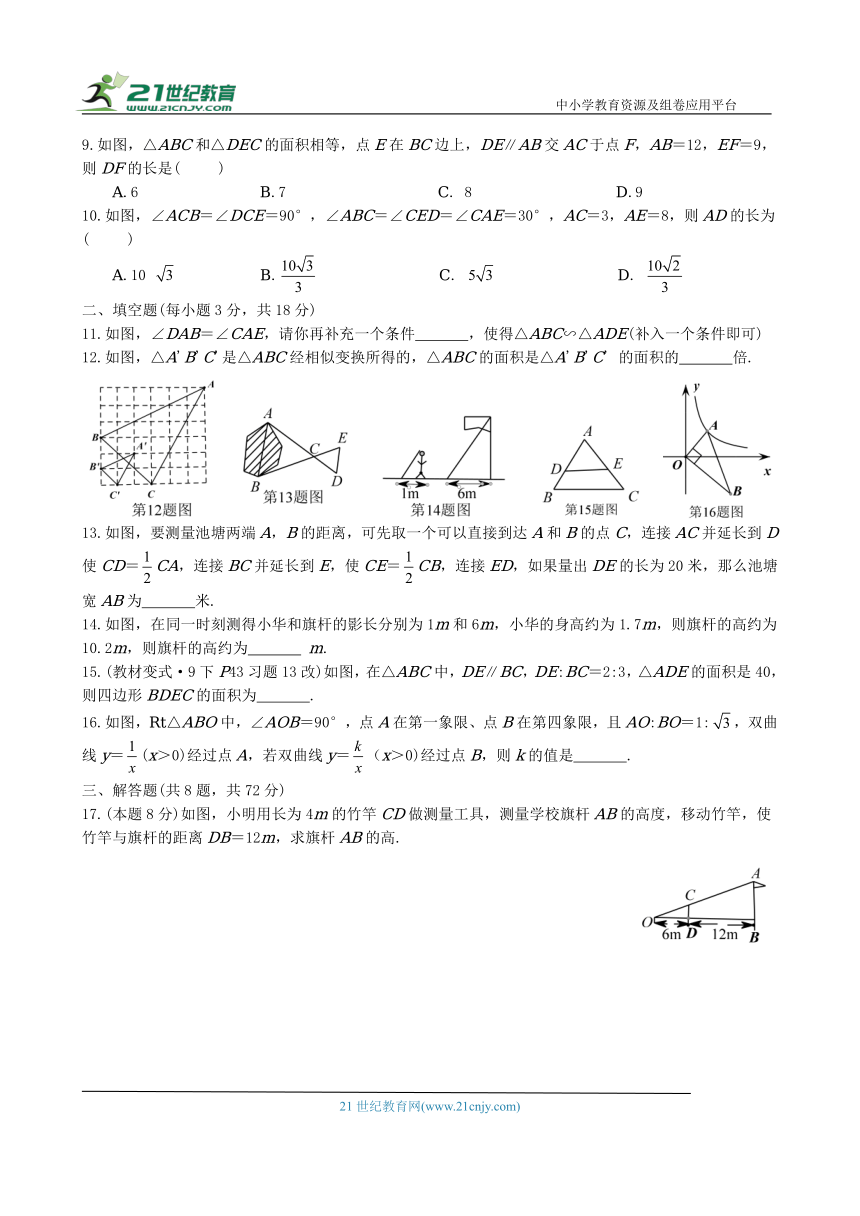
9.如图,△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是( )
A.6 B.7 C. 8 D.9
10.如图,∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,则AD的长为( )
A.10 B. C. D.
二、填空题(每小题3分,共18分)
11.如图,∠DAB=∠CAE,请你再补充一个条件 ,使得△ABC∽△ADE(补入一个条件即可)
12.如图,△A'B'C'是△ABC经相似变换所得的,△ABC的面积是△A'B'C' 的面积的 倍.
13.如图,要测量池塘两端A,B的距离,可先取一个可以直接到达A和B的点C,连接AC并延长到D使CD=CA,连接BC并延长到E,使CE=CB,连接ED,如果量出DE的长为20米,那么池塘宽AB为 米.
14.如图,在同一时刻测得小华和旗杆的影长分别为1m和6m,小华的身高约为1.7m,则旗杆的高约为10.2m,则旗杆的高约为 m.
15.(教材变式·9下P43习题13改)如图,在△ABC中,DE∥BC,DE:BC=2:3,△ADE的面积是40,则四边形BDEC的面积为 .
16.如图,Rt△ABO中,∠AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1:,双曲线y=(x>0)经过点A,若双曲线y=(x>0)经过点B,则k的值是 .
三、解答题(共8题,共72分)
17.(本题8分)如图,小明用长为4m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,求旗杆AB的高.
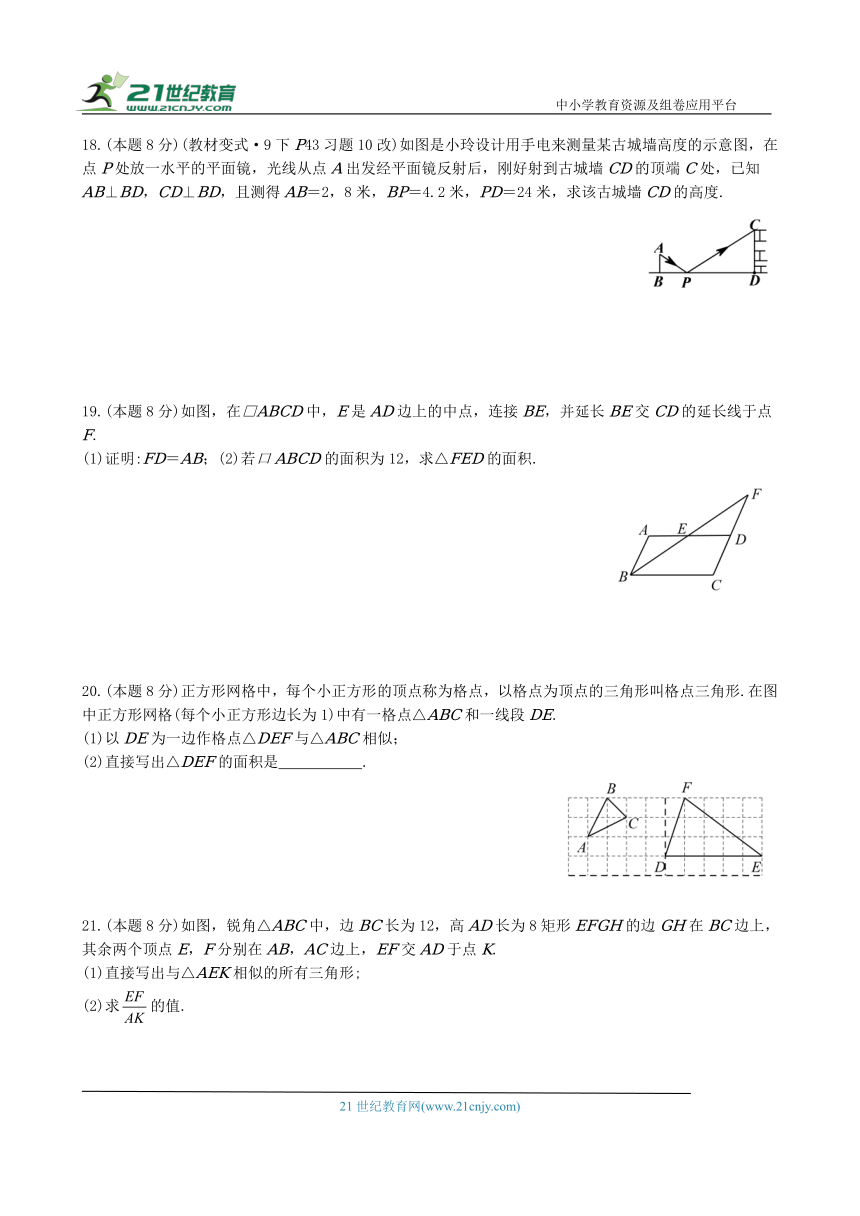
18.(本题8分)(教材变式·9下P43习题10改)如图是小玲设计用手电来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=2,8米,BP=4.2米,PD=24米,求该古城墙CD的高度.
19.(本题8分)如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
(1)证明:FD=AB;(2)若口ABCD的面积为12,求△FED的面积.
20.(本题8分)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.在图中正方形网格(每个小正方形边长为1)中有一格点△ABC和一线段DE.
(1)以DE为一边作格点△DEF与△ABC相似;
(2)直接写出△DEF的面积是 .
21.(本题8分)如图,锐角△ABC中,边BC长为12,高AD长为8矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC边上,EF交AD于点K.
(1)直接写出与△AEK相似的所有三角形;
(2)求的值.
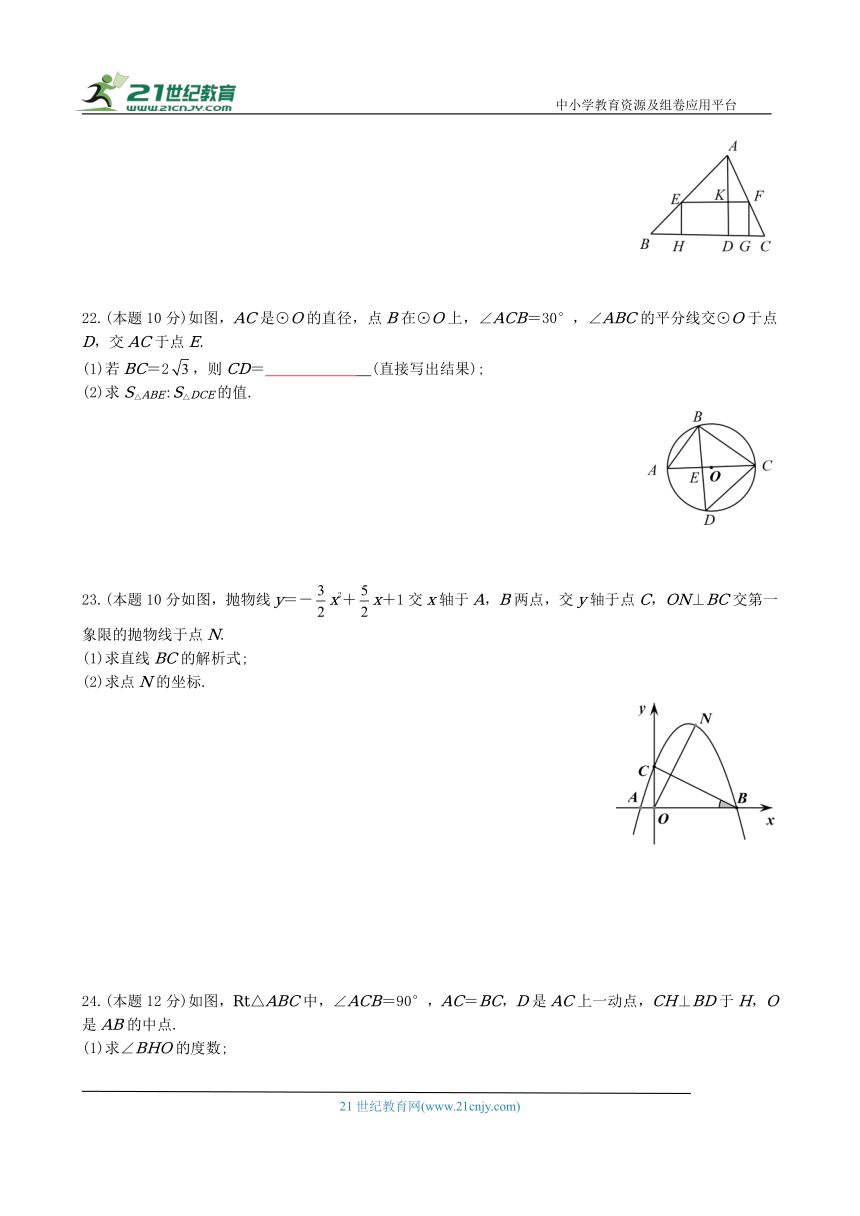
22.(本题10分)如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°,∠ABC的平分线交⊙O于点D,交AC于点E.
(1)若BC=2,则CD= (直接写出结果);
(2)求S△ABE:S△DCE的值.
23.(本题10分如图,抛物线y=-x2+x+1交x轴于A,B两点,交y轴于点C,ON⊥BC交第一象限的抛物线于点N.
(1)求直线BC的解析式;
(2)求点N的坐标.
24.(本题12分)如图,Rt△ABC中,∠ACB=90°,AC=BC,D是AC上一动点,CH⊥BD于H,O是AB的中点.
(1)求∠BHO的度数;
(2)若AD=CD,求的值;
(3)请直接写出= 时,CH=OH.
30.九年级数学(下)第27章《相似》周练(二)
(考试范围:第27.2∽27.3 解答参考时间:90分钟 满分120分)
一选择题(每小题3分,共30分)
1.已知△ABC∽△DEF,且相似比AB:DE=1:4,则△ABC与△DEF的对应高之比为( C )
A.1:2 B.2:1 C.1:4 D.4:1
2.若△ABC∽△A′B′C′,且相似比为2:1,则△ABC与△A′B′C′的周长之比为( B )
A.1:2 B.2:1 C.1:4 D.4:1
3.如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( C )
A.1:3 B.2:3 C.1:4 D.1:2
4.如图,在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为 ( B )
A.(2,0) B.(2,1) C.(3,3) D.(3,1)
5.(教材变式·9下P57习题7改)如图,零件的外径为17cm,要求它的壁厚x,需要先求出内径AB,现用一个交叉钳(AC与BD相等)去量,若测得OA:OC=OB:OD=3:1,CD=5cm,零件的壁厚x等于( B )
A.2cm B.1cm C.0.5cm D.3cm
6.如图,在□ABCD中E为CD上一点,连接AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:DC等于( A )
7.如图,D是△ABC的边BC上一点,已知AB=4,AD=2.∠DAC=∠B,若△ABD的面积为9,则△ACD的面积为( B )
A.2 B.3 C.4 D.6
8.如图,在等边△ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( D ).
A.2:3 B. :2 C. :3 D.1:3
第8题图 第9题图 第10题图
9.如图,△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是( B )
A.6 B.7 C. 8 D.9
10.如图,∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,则AD的长为( B )
A.10 B. C. D.
二、填空题(每小题3分,共18分)
11.如图,∠DAB=∠CAE,请你再补充一个条件∠D=∠B,使得△ABC∽△ADE(补入一个条件即可)
12.如图,△A'B'C'是△ABC经相似变换所得的,△ABC的面积是△A'B'C' 的面积的 9 倍.
13.如图,要测量池塘两端A,B的距离,可先取一个可以直接到达A和B的点C,连接AC并延长到D使CD=CA,连接BC并延长到E,使CE=CB,连接ED,如果量出DE的长为20米,那么池塘宽AB为 40 米.
14.如图,在同一时刻测得小华和旗杆的影长分别为1m和6m,小华的身高约为1.7m,则旗杆的高约为10.2m,则旗杆的高约为 10.2 m.
15.(教材变式·9下P43习题13改)如图,在△ABC中,DE∥BC,DE:BC=2:3,△ADE的面积是40,则四边形BDEC的面积为 50 .
16.如图,Rt△ABO中,∠AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1:,双曲线y=(x>0)经过点A,若双曲线y=(x>0)经过点B,则k的值是 -3 .
三、解答题(共8题,共72分)
17.(本题8分)如图,小明用长为4m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,求旗杆AB的高.
解:AB=12m.
18.(本题8分)(教材变式·9下P43习题10改)如图是小玲设计用手电来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=2,8米,BP=4.2米,PD=24米,求该古城墙CD的高度.
解:CD=16米.
19.(本题8分)如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
(1)证明:FD=AB;(2)若口ABCD的面积为12,求△FED的面积.
解:(1)证△ABE≌△DFE(AAS),∴FD=AB;
(2)∵DE∥BC,△FED∽△FBC,
∵△ABE≌△DFE.∴BE=EF,S△FBC=S平行四边形ABCD,
∴=,∴=∴=.
∴△FED的面积为3.
20.(本题8分)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.在图中正方形网格(每个小正方形边长为1)中有一格点△ABC和一线段DE.
(1)以DE为一边作格点△DEF与△ABC相似;
(2)直接写出△DEF的面积是 .
解:(1)略;(2)7.5.
21.(本题8分)如图,锐角△ABC中,边BC长为12,高AD长为8矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC边上,EF交AD于点K.
(1)直接写出与△AEK相似的所有三角形;
(2)求的值.
解:(1)△EBH,△ABD.
(2) ===.
22.(本题10分)如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°,∠ABC的平分线交⊙O于点D,交AC于点E.
(1)若BC=2,则CD= (直接写出结果);
(2)求S△ABE:S△DCE的值.
解:(1)2;
(2)易证△ABE∽△DCE设AB=x则AC=2x,CD=AC=x,
∴===.
23.(本题10分)如图,抛物线y=-x2+x+1交x轴于A,B两点,交y轴于点C,ON⊥BC交第一象限的抛物线于点N.(1)求直线BC的解析式; (2)求点N的坐标.
解:(1)易求B(2,0),C(0,1),∴y=x+1;
(2)作NP⊥x轴于点P,设N(t, -t2+t+1),△OPN∽△COB, =,
2OP=PN,OP=t, -t2+t+1=2t,t1=1,t2=-(舍去),∴N(1,2).
24.(本题12分)如图,Rt△ABC中,∠ACB=90°,AC=BC,D是AC上一动点,CH⊥BD于H,O是AB的中点.
(1)求∠BHO的度数;
(2)若AD=CD,求的值;
(3)请直接写出= 时,CH=OH.
解:(1)∠BHO=45°(提示:方法一:在BH上截取BE=CH,连OE,
易证△COH≌△BOE,等腰Rt△OEH,∴∠BHO=45°,
方法二:连CO,则CO⊥AB,可证C,H,O,B四点共圆,得∠BHO=∠BCO=45°,
方法三:由CB2=BH·BD,BC2=BO·BA进一步得得= ,∠OBH=∠ABD,
∴△BOH∽△BDA,∴∠BHO=∠A=45°)
(2)由△BHO∽△BAD==,
设BD=,BO=2,则AB=4,BC=2,
在Rt△BCD中,BD2=BC2+CD2,
∴()2=(2)2+CD2,∴CD=,
又AC=BC=2,∴CD=AD.即D是AC中点.
(3)(提示:△BOH∽△BAD=,△BCH∽△BDC,又CH=OH,∴=,∴==).
21世纪教育网(www.21cnjy.com)
30.九年级数学(下)第27章《相似》周练(二)
(考试范围:第27.2∽27.3 解答参考时间:90分钟 满分120分)
一选择题(每小题3分,共30分)
1.已知△ABC∽△DEF,且相似比AB:DE=1:4,则△ABC与△DEF的对应高之比为( )
A.1:2 B.2:1 C.1:4 D.4:1
2.若△ABC∽△A′B′C′,且相似比为2:1,则△ABC与△A′B′C′的周长之比为( )
A.1:2 B.2:1 C.1:4 D.4:1
3.如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( )
A.1:3 B.2:3 C.1:4 D.1:2
4.如图,在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,0) B.(2,1) C.(3,3) D.(3,1)
5.(教材变式·9下P57习题7改)如图,零件的外径为17cm,要求它的壁厚x,需要先求出内径AB,现用一个交叉钳(AC与BD相等)去量,若测得OA:OC=OB:OD=3:1,CD=5cm,零件的壁厚x等于( )
A.2cm B.1cm C.0.5cm D.3cm
6.如图,在□ABCD中E为CD上一点,连接AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:DC等于( )
7.如图,D是△ABC的边BC上一点,已知AB=4,AD=2.∠DAC=∠B,若△ABD的面积为9,则△ACD的面积为( )
A.2 B.3 C.4 D.6
8.如图,在等边△ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )
A.2:3 B. :2 C. :3 D.1:3
第8题图 第9题图 第10题图
9.如图,△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是( )
A.6 B.7 C. 8 D.9
10.如图,∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,则AD的长为( )
A.10 B. C. D.
二、填空题(每小题3分,共18分)
11.如图,∠DAB=∠CAE,请你再补充一个条件 ,使得△ABC∽△ADE(补入一个条件即可)
12.如图,△A'B'C'是△ABC经相似变换所得的,△ABC的面积是△A'B'C' 的面积的 倍.
13.如图,要测量池塘两端A,B的距离,可先取一个可以直接到达A和B的点C,连接AC并延长到D使CD=CA,连接BC并延长到E,使CE=CB,连接ED,如果量出DE的长为20米,那么池塘宽AB为 米.
14.如图,在同一时刻测得小华和旗杆的影长分别为1m和6m,小华的身高约为1.7m,则旗杆的高约为10.2m,则旗杆的高约为 m.
15.(教材变式·9下P43习题13改)如图,在△ABC中,DE∥BC,DE:BC=2:3,△ADE的面积是40,则四边形BDEC的面积为 .
16.如图,Rt△ABO中,∠AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1:,双曲线y=(x>0)经过点A,若双曲线y=(x>0)经过点B,则k的值是 .
三、解答题(共8题,共72分)
17.(本题8分)如图,小明用长为4m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,求旗杆AB的高.
18.(本题8分)(教材变式·9下P43习题10改)如图是小玲设计用手电来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=2,8米,BP=4.2米,PD=24米,求该古城墙CD的高度.
19.(本题8分)如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
(1)证明:FD=AB;(2)若口ABCD的面积为12,求△FED的面积.
20.(本题8分)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.在图中正方形网格(每个小正方形边长为1)中有一格点△ABC和一线段DE.
(1)以DE为一边作格点△DEF与△ABC相似;
(2)直接写出△DEF的面积是 .
21.(本题8分)如图,锐角△ABC中,边BC长为12,高AD长为8矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC边上,EF交AD于点K.
(1)直接写出与△AEK相似的所有三角形;
(2)求的值.
22.(本题10分)如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°,∠ABC的平分线交⊙O于点D,交AC于点E.
(1)若BC=2,则CD= (直接写出结果);
(2)求S△ABE:S△DCE的值.
23.(本题10分如图,抛物线y=-x2+x+1交x轴于A,B两点,交y轴于点C,ON⊥BC交第一象限的抛物线于点N.
(1)求直线BC的解析式;
(2)求点N的坐标.
24.(本题12分)如图,Rt△ABC中,∠ACB=90°,AC=BC,D是AC上一动点,CH⊥BD于H,O是AB的中点.
(1)求∠BHO的度数;
(2)若AD=CD,求的值;
(3)请直接写出= 时,CH=OH.
30.九年级数学(下)第27章《相似》周练(二)
(考试范围:第27.2∽27.3 解答参考时间:90分钟 满分120分)
一选择题(每小题3分,共30分)
1.已知△ABC∽△DEF,且相似比AB:DE=1:4,则△ABC与△DEF的对应高之比为( C )
A.1:2 B.2:1 C.1:4 D.4:1
2.若△ABC∽△A′B′C′,且相似比为2:1,则△ABC与△A′B′C′的周长之比为( B )
A.1:2 B.2:1 C.1:4 D.4:1
3.如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△COB等于( C )
A.1:3 B.2:3 C.1:4 D.1:2
4.如图,在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为 ( B )
A.(2,0) B.(2,1) C.(3,3) D.(3,1)
5.(教材变式·9下P57习题7改)如图,零件的外径为17cm,要求它的壁厚x,需要先求出内径AB,现用一个交叉钳(AC与BD相等)去量,若测得OA:OC=OB:OD=3:1,CD=5cm,零件的壁厚x等于( B )
A.2cm B.1cm C.0.5cm D.3cm
6.如图,在□ABCD中E为CD上一点,连接AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:DC等于( A )
7.如图,D是△ABC的边BC上一点,已知AB=4,AD=2.∠DAC=∠B,若△ABD的面积为9,则△ACD的面积为( B )
A.2 B.3 C.4 D.6
8.如图,在等边△ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( D ).
A.2:3 B. :2 C. :3 D.1:3
第8题图 第9题图 第10题图
9.如图,△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是( B )
A.6 B.7 C. 8 D.9
10.如图,∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,则AD的长为( B )
A.10 B. C. D.
二、填空题(每小题3分,共18分)
11.如图,∠DAB=∠CAE,请你再补充一个条件∠D=∠B,使得△ABC∽△ADE(补入一个条件即可)
12.如图,△A'B'C'是△ABC经相似变换所得的,△ABC的面积是△A'B'C' 的面积的 9 倍.
13.如图,要测量池塘两端A,B的距离,可先取一个可以直接到达A和B的点C,连接AC并延长到D使CD=CA,连接BC并延长到E,使CE=CB,连接ED,如果量出DE的长为20米,那么池塘宽AB为 40 米.
14.如图,在同一时刻测得小华和旗杆的影长分别为1m和6m,小华的身高约为1.7m,则旗杆的高约为10.2m,则旗杆的高约为 10.2 m.
15.(教材变式·9下P43习题13改)如图,在△ABC中,DE∥BC,DE:BC=2:3,△ADE的面积是40,则四边形BDEC的面积为 50 .
16.如图,Rt△ABO中,∠AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1:,双曲线y=(x>0)经过点A,若双曲线y=(x>0)经过点B,则k的值是 -3 .
三、解答题(共8题,共72分)
17.(本题8分)如图,小明用长为4m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,求旗杆AB的高.
解:AB=12m.
18.(本题8分)(教材变式·9下P43习题10改)如图是小玲设计用手电来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=2,8米,BP=4.2米,PD=24米,求该古城墙CD的高度.
解:CD=16米.
19.(本题8分)如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
(1)证明:FD=AB;(2)若口ABCD的面积为12,求△FED的面积.
解:(1)证△ABE≌△DFE(AAS),∴FD=AB;
(2)∵DE∥BC,△FED∽△FBC,
∵△ABE≌△DFE.∴BE=EF,S△FBC=S平行四边形ABCD,
∴=,∴=∴=.
∴△FED的面积为3.
20.(本题8分)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.在图中正方形网格(每个小正方形边长为1)中有一格点△ABC和一线段DE.
(1)以DE为一边作格点△DEF与△ABC相似;
(2)直接写出△DEF的面积是 .
解:(1)略;(2)7.5.
21.(本题8分)如图,锐角△ABC中,边BC长为12,高AD长为8矩形EFGH的边GH在BC边上,其余两个顶点E,F分别在AB,AC边上,EF交AD于点K.
(1)直接写出与△AEK相似的所有三角形;
(2)求的值.
解:(1)△EBH,△ABD.
(2) ===.
22.(本题10分)如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°,∠ABC的平分线交⊙O于点D,交AC于点E.
(1)若BC=2,则CD= (直接写出结果);
(2)求S△ABE:S△DCE的值.
解:(1)2;
(2)易证△ABE∽△DCE设AB=x则AC=2x,CD=AC=x,
∴===.
23.(本题10分)如图,抛物线y=-x2+x+1交x轴于A,B两点,交y轴于点C,ON⊥BC交第一象限的抛物线于点N.(1)求直线BC的解析式; (2)求点N的坐标.
解:(1)易求B(2,0),C(0,1),∴y=x+1;
(2)作NP⊥x轴于点P,设N(t, -t2+t+1),△OPN∽△COB, =,
2OP=PN,OP=t, -t2+t+1=2t,t1=1,t2=-(舍去),∴N(1,2).
24.(本题12分)如图,Rt△ABC中,∠ACB=90°,AC=BC,D是AC上一动点,CH⊥BD于H,O是AB的中点.
(1)求∠BHO的度数;
(2)若AD=CD,求的值;
(3)请直接写出= 时,CH=OH.
解:(1)∠BHO=45°(提示:方法一:在BH上截取BE=CH,连OE,
易证△COH≌△BOE,等腰Rt△OEH,∴∠BHO=45°,
方法二:连CO,则CO⊥AB,可证C,H,O,B四点共圆,得∠BHO=∠BCO=45°,
方法三:由CB2=BH·BD,BC2=BO·BA进一步得得= ,∠OBH=∠ABD,
∴△BOH∽△BDA,∴∠BHO=∠A=45°)
(2)由△BHO∽△BAD==,
设BD=,BO=2,则AB=4,BC=2,
在Rt△BCD中,BD2=BC2+CD2,
∴()2=(2)2+CD2,∴CD=,
又AC=BC=2,∴CD=AD.即D是AC中点.
(3)(提示:△BOH∽△BAD=,△BCH∽△BDC,又CH=OH,∴=,∴==).
21世纪教育网(www.21cnjy.com)
